Chapter 9 Risk And Return The Linear Relationships

Chapter 9 Risk And Return: The Linear Relationships And The Capital Asset Pricing Model ® 3/19/20181999 South-Western College Publishing 1

Characteristics Of Indifference Curves • All Combinations [E(R), R] – Provide the investor with the same level of utility • Moving to a Higher Indifference Curve – Increases the investors utility • Subjective – Slopes differ from one investor to another ® 3/19/20181999 South-Western College Publishing 2

Capital Market Theory: An Overview • Capital market theory extends portfolio theory and develops a model for pricing all risky assets • Capital asset pricing model (CAPM) will allow you to determine the required rate of return for any risky asset ® 3/19/20181999 South-Western College Publishing 3

Assumptions of Capital Market Theory 1. All investors are Markowitz efficient investors who want to target points on the efficient frontier. – The exact location on the efficient frontier and, therefore, the specific portfolio selected, will depend on the individual investor’s risk-return utility function. ® 3/19/20181999 South-Western College Publishing 4

Assumptions of Capital Market Theory 2. Investors can borrow or lend any amount of money at the risk-free rate of return (RFR). – Clearly it is always possible to lend money at the nominal risk-free rate by buying risk-free securities such as government T-bils. It is not always possible to borrow at this risk-free rate, but we will see that assuming a higher borrowing rate does not change the general results. ® 3/19/20181999 South-Western College Publishing 5

Assumptions of Capital Market Theory 3. All investors have homogeneous expectations; that is, they estimate identical probability distributions for future rates of return. – Again, this assumption can be relaxed. As long as the differences in expectations are not vast, their effects are minor. ® 3/19/20181999 South-Western College Publishing 6

Assumptions of Capital Market Theory 4. All investors have the same one-period time horizon such as one-month, six months, or one year. – The model will be developed for a single hypothetical period, and its results could be affected by a different assumption. A difference in the time horizon would require investors to derive risk measures and risk-free assets that are consistent with their time horizons. ® 3/19/20181999 South-Western College Publishing 7

Assumptions of Capital Market Theory 5. All investments are infinitely divisible, which means that it is possible to buy or sell fractional shares of any asset or portfolio. – This assumption allows us to discuss investment alternatives as continuous curves. Changing it would have little impact on theory. ® 3/19/20181999 South-Western College Publishing 8

Assumptions of Capital Market Theory 6. There are no taxes or transaction costs involved in buying or selling assets. – This is a reasonable assumption in many instances. Neither pension funds nor religious groups have to pay taxes, and the transaction costs for most financial institutions are less than 1 percent on most financial instruments. Again, relaxing this assumption modifies the results, but does not change the basic thrust. ® 3/19/20181999 South-Western College Publishing 9

Assumptions of Capital Market Theory 7. There is no inflation or any change in interest rates, or inflation is fully anticipated. – This is a reasonable initial assumption, and it can be modified. ® 3/19/20181999 South-Western College Publishing 10

Assumptions of Capital Market Theory 8. Capital markets are in equilibrium. – This means that we begin with all investments properly priced in line with their risk levels. ® 3/19/20181999 South-Western College Publishing 11

Assumptions of Capital Market Theory • Some of these assumptions are unrealistic • Relaxing many of these assumptions would have only minor influence on the model and would not change its main implications or conclusions. • Judge a theory on how well it explains and helps predict behavior, not on its assumptions. ® 3/19/20181999 South-Western College Publishing 12

Risk-Free Asset • • An asset with zero variance Zero correlation with all other risky assets Provides the risk-free rate of return (RFR) Will lie on the vertical axis of a portfolio graph ® 3/19/20181999 South-Western College Publishing 13

Risk-Free Asset Covariance between two sets of returns is Because the returns for the risk free asset are certain, Thus Ri = E(Ri), and Ri - E(Ri) = 0 Consequently, the covariance of the risk-free asset with any risky asset or portfolio will always equal zero. Similarly the correlation between any risky asset and the risk-free asset would be zero. 14 ® 3/19/20181999 South-Western College Publishing

Combining a Risk-Free Asset with a Risky Portfolio Expected return the weighted average of the two returns This is a linear relationship ® 3/19/20181999 South-Western College Publishing 15

Combining a Risk-Free Asset with a Risky Portfolio Standard deviation The expected variance for a two-asset portfolio is Substituting the risk-free asset for Security 1, and the risky asset for Security 2, this formula would become Since we know that the variance of the risk-free asset is zero and the correlation between the risk-free asset and any risky asset i is zero we can adjust the formula ® 3/19/20181999 South-Western College Publishing 16

Combining a Risk-Free Asset with a Risky Portfolio Given the variance formula the standard deviation is Therefore, the standard deviation of a portfolio that combines the risk-free asset with risky assets is the linear proportion of the standard deviation of the risky asset portfolio. ® 3/19/20181999 South-Western College Publishing 17

Combining a Risk-Free Asset with a Risky Portfolio Since both the expected return and the standard deviation of return for such a portfolio are linear combinations, a graph of possible portfolio returns and risks looks like a straight line between the two assets. ® 3/19/20181999 South-Western College Publishing 18

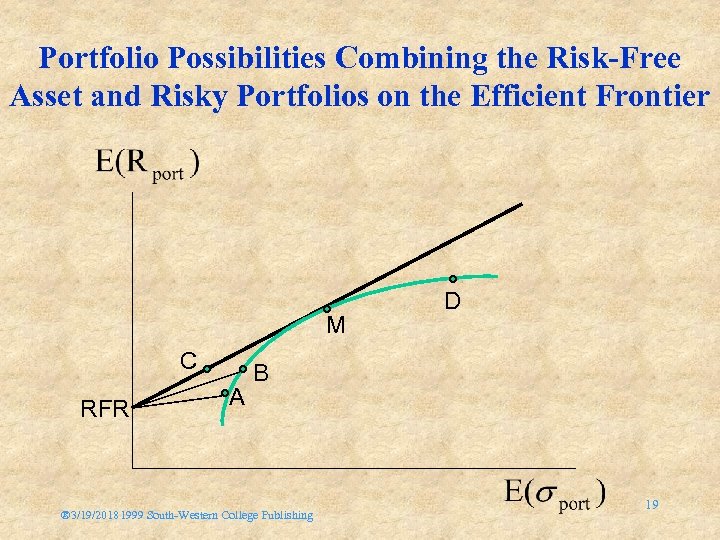Portfolio Possibilities Combining the Risk-Free Asset and Risky Portfolios on the Efficient Frontier M C RFR A D B ® 3/19/20181999 South-Western College Publishing 19

The efficient frontier is expanded when risk-free borrowing or lending is allowed. Slide 19 ® 3/19/20181999 South-Western College Publishing 20

Risk-Return Possibilities with Leverage To attain a higher expected return than is available at point M (in exchange for accepting higher risk) Either invest along the efficient frontier beyond point M, such as point D Or, add leverage to the portfolio by borrowing money at the risk-free rate and investing in the risky portfolio at point M ® 3/19/20181999 South-Western College Publishing 21

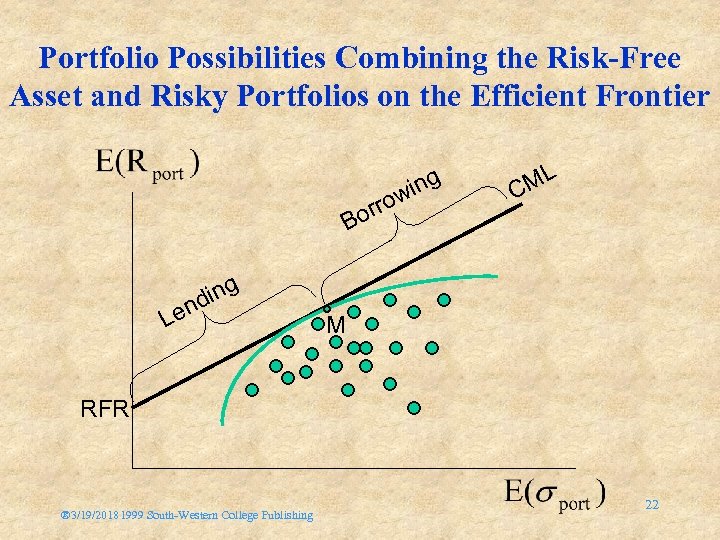Portfolio Possibilities Combining the Risk-Free Asset and Risky Portfolios on the Efficient Frontier orr B ing nd Le o ing w ML C M RFR ® 3/19/20181999 South-Western College Publishing 22

E(R) CML E(Rm) [E(Rm) - r]/ m m ® 3/19/20181999 South-Western College Publishing 23

The Market Portfolio Because portfolio M lies at the point of tangency, it has the highest portfolio possibility line Everybody will want to invest in Portfolio M and borrow or lend to be somewhere on the CML Therefore this portfolio must include ALL RISKY ASSETS ® 3/19/20181999 South-Western College Publishing 24

The Market Portfolio Because the market is in equilibrium, all assets are included in this portfolio in proportion to their market value ® 3/19/20181999 South-Western College Publishing 25

The Market Portfolio Because it contains all risky assets, it is a completely diversified portfolio, which means that all the unique risk of individual assets (unsystematic risk) is diversified away ® 3/19/20181999 South-Western College Publishing 26

Systematic Risk Only systematic risk remains in the market portfolio Systematic risk is the variability in all risky assets caused by macroeconomic variables Systematic risk can be measured by the standard deviation of returns of the market portfolio and can change over time ® 3/19/20181999 South-Western College Publishing 27

Examples of Macroeconomic Factors Affecting Systematic Risk • Variability in growth of money supply • Interest rate volatility • Variability in industrial production corporate earnings and cash flow ® 3/19/20181999 South-Western College Publishing 28

How to Measure Diversification All portfolios on the CML are perfectly positively correlated with each other and with the completely diversified market Portfolio M A completely diversified portfolio would have a correlation with the market portfolio of +1. 00 ® 3/19/20181999 South-Western College Publishing 29

Diversification and the Elimination of Unsystematic Risk The purpose of diversification is to reduce the standard deviation of the total portfolio This assumes that imperfect correlations exist among securities As you add securities, you expect the average covariance for the portfolio to decline How many securities must you add to obtain a completely diversified portfolio? ® 3/19/20181999 South-Western College Publishing 30

Diversification and the Elimination of Unsystematic Risk Observe what happens as you increase the sample size of the portfolio by adding securities that have some positive correlation ® 3/19/20181999 South-Western College Publishing 31

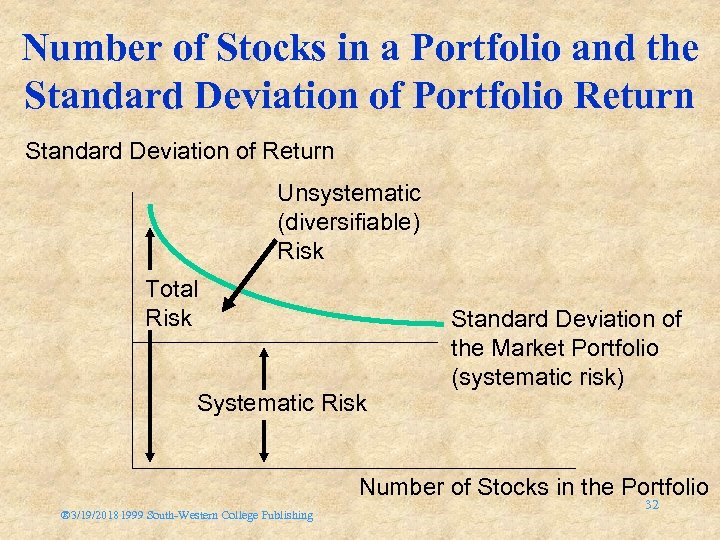Number of Stocks in a Portfolio and the Standard Deviation of Portfolio Return Standard Deviation of Return Unsystematic (diversifiable) Risk Total Risk Systematic Risk Standard Deviation of the Market Portfolio (systematic risk) Number of Stocks in the Portfolio ® 3/19/20181999 South-Western College Publishing 32

The CML and the Separation Theorem The CML leads all investors to invest in the M portfolio Individual investors should differ in position on the CML depending on risk preferences How an investor gets to a point on the CML is based on financing decisions Risk averse investors will lend part of the portfolio at the risk-free rate and invest the remainder in the market portfolio ® 3/19/20181999 South-Western College Publishing 33

The CML and the Separation Theorem Investors preferring more risk might borrow funds at the RFR and invest everything in the market portfolio ® 3/19/20181999 South-Western College Publishing 34

The CML and the Separation Theorem The decision of both investors is to invest in portfolio M along the CML (the investment decision) ® 3/19/20181999 South-Western College Publishing 35

The CML and the Separation Theorem The decision to borrow or lend to obtain a point on the CML is a separate decision based on risk preferences (financing decision) ® 3/19/20181999 South-Western College Publishing 36

The CML and the Separation Theorem Tobin refers to this separation of the investment decision from the financing decision the separation theorem ® 3/19/20181999 South-Western College Publishing 37

Separation Property • Two Stages – Find portfolio m objective – Maximize utility by borrowing and lending subjective • Linear Relationship – Between E(R) and ® 3/19/20181999 South-Western College Publishing 38

A Risk Measure for the CML Covariance with the M portfolio is the systematic risk of an asset The Markowitz portfolio model considers the average covariance with all other assets in the portfolio The only relevant portfolio is the M portfolio ® 3/19/20181999 South-Western College Publishing 39

A Risk Measure for the CML Together, this means the only important consideration is the asset’s covariance with the market portfolio ® 3/19/20181999 South-Western College Publishing 40

Systematic Risk Only Systematic Risk Is Relevant! ® 3/19/20181999 South-Western College Publishing 41

A Risk Measure for the CML Because all individual risky assets are part of the M portfolio, an asset’s rate of return in relation to the return for the M portfolio may be described using the following linear model: where: Rit = return for asset i during period t ai = constant term for asset i bi = slope coefficient for asset i RMt = return for the M portfolio during period t = random error term ® 3/19/20181999 South-Western College Publishing 42

Variance of Returns for a Risky Asset ® 3/19/20181999 South-Western College Publishing 43

The Capital Asset Pricing Model: Expected Return and Risk • The existence of a risk-free asset resulted in deriving a capital market line (CML) that became the relevant frontier • An asset’s covariance with the market portfolio is the relevant risk measure • This can be used to determine an appropriate expected rate of return on a risky asset - the capital asset pricing model (CAPM) ® 3/19/20181999 South-Western College Publishing 44

The Capital Asset Pricing Model: Expected Return and Risk • CAPM indicates what should be the expected or required rates of return on risky assets • This helps to value an asset by providing an appropriate discount rate to use in dividend valuation models • You can compare an estimated rate of return to the required rate of return implied by CAPM - over/ under valued ? ® 3/19/20181999 South-Western College Publishing 45

The Security Market Line (SML) • The relevant risk measure for an individual risky asset is its covariance with the market portfolio (Covi, m) • This is shown as the risk measure • The return for the market portfolio should be consistent with its own risk, which is the covariance of the market with itself - or its variance: ® 3/19/20181999 South-Western College Publishing 46

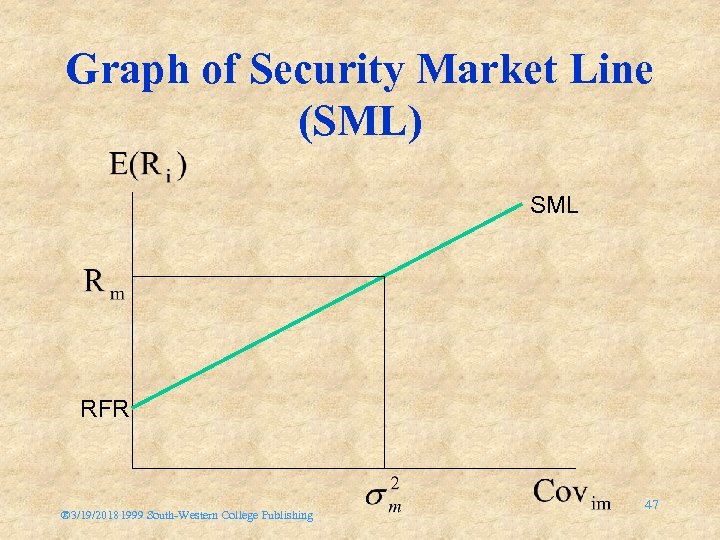Graph of Security Market Line (SML) SML RFR ® 3/19/20181999 South-Western College Publishing 47

The Security Market Line (SML) The equation for the risk-return line is We then define ® 3/19/20181999 South-Western College Publishing as beta 48

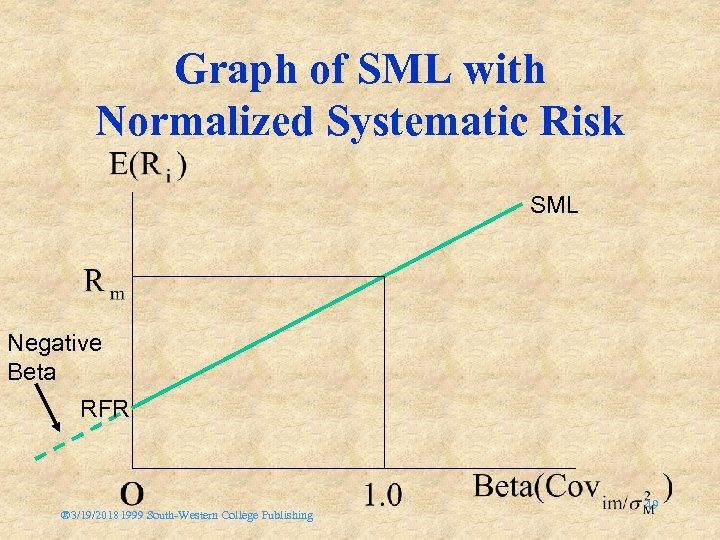Graph of SML with Normalized Systematic Risk SML Negative Beta RFR ® 3/19/20181999 South-Western College Publishing 49

Determining the Expected Rate of Return for a Risky Asset The expected rate of return of a risk asset is determined by the RFR plus a risk premium for the individual asset The risk premium is determined by the systematic risk of the asset (beta) and the prevailing market risk premium (RM-RFR) ® 3/19/20181999 South-Western College Publishing 50

Risk Premium • [E(Rm) - r] is the Risk Premium on the Portfolio m • E(Rm) - r = [E(Rm) - r] i • The Larger the , the Larger the Risk Premium ® 3/19/20181999 South-Western College Publishing 51

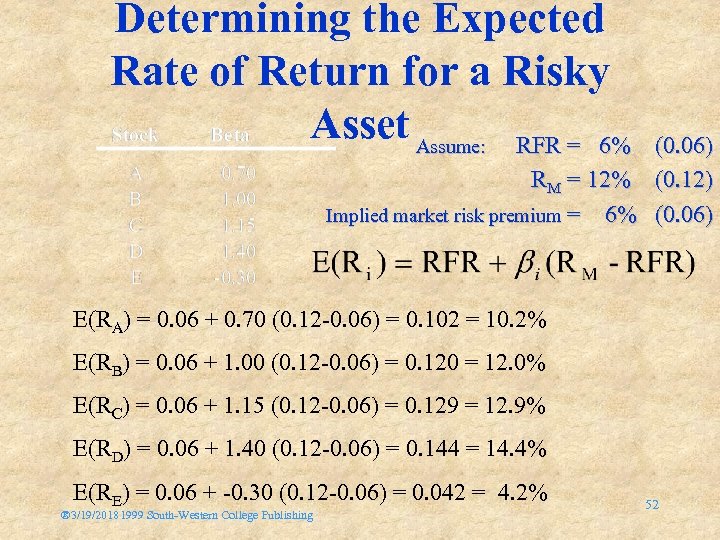Determining the Expected Rate of Return for a Risky Asset Assume: RFR = 6% (0. 06) RM = 12% (0. 12) Implied market risk premium = 6% (0. 06) E(RA) = 0. 06 + 0. 70 (0. 12 -0. 06) = 0. 102 = 10. 2% E(RB) = 0. 06 + 1. 00 (0. 12 -0. 06) = 0. 120 = 12. 0% E(RC) = 0. 06 + 1. 15 (0. 12 -0. 06) = 0. 129 = 12. 9% E(RD) = 0. 06 + 1. 40 (0. 12 -0. 06) = 0. 144 = 14. 4% E(RE) = 0. 06 + -0. 30 (0. 12 -0. 06) = 0. 042 = 4. 2% ® 3/19/20181999 South-Western College Publishing 52

Determining the Expected Rate of Return for a Risky Asset In equilibrium, all assets and all portfolios of assets should plot on the SML Any security with an estimated return that plots above the SML is underpriced Any security with an estimated return that plots below the SML is overpriced A superior investor must derive value estimates for assets that are consistently superior to the consensus market evaluation to earn better risk-adjusted rates of return than the average investor ® 3/19/20181999 South-Western College Publishing 53

Identifying Undervalued and Overvalued Assets Compare the required rate of return to the expected rate of return for a specific risky asset using the SML over a specific investment horizon to determine if it is an appropriate investment Independent estimates of return for the securities provide price and dividend outlooks ® 3/19/20181999 South-Western College Publishing 54

Price, Dividend, and Rate of Return Estimates ® 3/19/20181999 South-Western College Publishing 55

Comparison of Required Rate of Return to Estimated Rate of Return ® 3/19/20181999 South-Western College Publishing 56

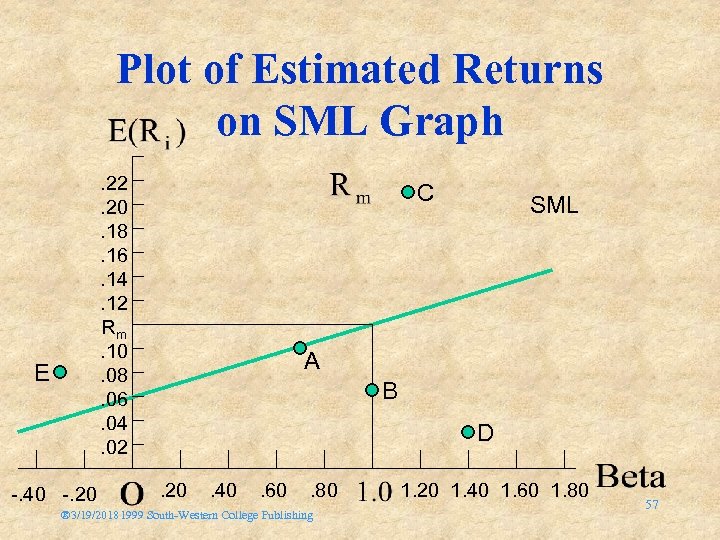Plot of Estimated Returns on SML Graph. 22. 20. 18. 16. 14. 12 Rm. 10. 08. 06. 04. 02 E -. 40 -. 20 C SML A B D. 20 . 40 . 60 . 80 ® 3/19/20181999 South-Western College Publishing 1. 20 1. 40 1. 60 1. 80 57

CAPM For Stock Selection • Excess or Abnormal Return • [E(Rp) - r] = i + [E(Rm) - r] i – Alpha i = excess return • Market is Efficient – i will disappear • [E(Rp) - r] = [E(Rm) - r] i ® 3/19/20181999 South-Western College Publishing 58

CAPM AS A Screening Tool • High-Alpha Stocks • Low-Alpha Stocks • Final Analysis – Dividends – Growth – Earnings surprise – Other variables ® 3/19/20181999 South-Western College Publishing 59

Proof Of The CAPM • SML Holds for all Efficient Portfolios Whose Returns are Rp E(Rp) = r + [E(Rm) - r] p • In Equilibrium – The linear relationship between E(R) and hold • SML ® 3/19/20181999 South-Western College Publishing 60

EPCo. R • Equilibrium • All Assets in the Portfolio – Contribute the same % to • Portfolio risk premium ® 3/19/20181999 South-Western College Publishing 61

Calculating Systematic Risk: The Characteristic Line The systematic risk input of an individual asset is derived from a regression model, referred to as the asset’s characteristic line with the model portfolio: where: Ri, t = the rate of return for asset i during period t RM, t = the rate of return for the market portfolio M during t ® 3/19/20181999 South-Western College Publishing 62

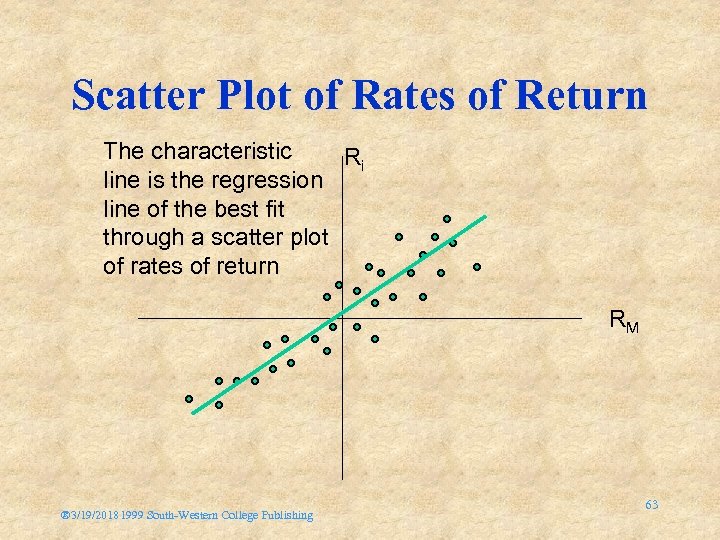Scatter Plot of Rates of Return The characteristic Ri line is the regression line of the best fit through a scatter plot of rates of return RM ® 3/19/20181999 South-Western College Publishing 63

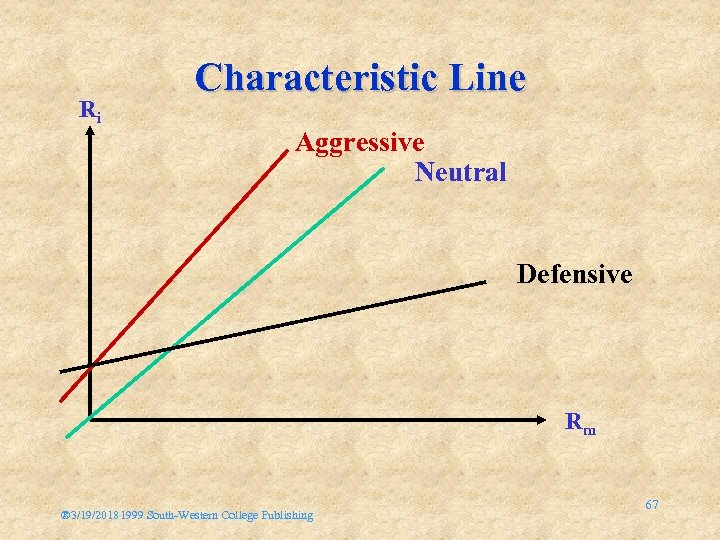
What Is Beta ( )? • Slope of the Characteristic Line • Measures Risk Systematic – Variance – Covariance of other assets in the portfolio – Individual assets – Portfolios • The Larger the – The more the risk ® 3/19/20181999 South-Western College Publishing 64

What Is The Meaning Of ? • i = 1 = Neutral Stock Market Stock • i > 1 = Aggressive Stock • i < 1 = Defensive Stock • r = 0 = Risk-Free Asset ® 3/19/20181999 South-Western College Publishing 65

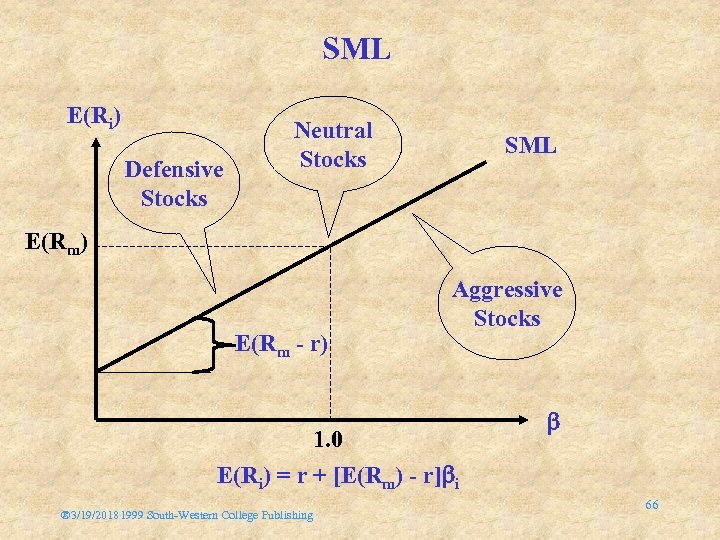SML E(Ri) Defensive Stocks Neutral Stocks SML E(Rm) E(Rm - r) Aggressive Stocks 1. 0 E(Ri) = r + [E(Rm) - r] i ® 3/19/20181999 South-Western College Publishing 66

Ri Characteristic Line Aggressive Neutral Defensive Rm ® 3/19/20181999 South-Western College Publishing 67

The Impact of the Time Interval Number of observations and time interval used in regression vary Value Line Investment Services (VL) uses weekly rates of return over five years Merrill Lynch, Pierce, Fenner & Smith (ML) uses monthly return over five years There is no “correct” interval for analysis Weak relationship between VL & ML betas due to difference in intervals used Interval effect impacts smaller firms more ® 3/19/20181999 South-Western College Publishing 68

The Effect of the Market Proxy The market portfolio of all risky assets must be represented in computing an asset’s characteristic line Standard & Poor’s 500 Composite Index is most often used – Large proportion of the total market value of U. S. stocks – Value weighted series ® 3/19/20181999 South-Western College Publishing 69

Weaknesses of Using S&P 500 as the Market Proxy – Includes only U. S. stocks – The theoretical market portfolio should include U. S. and non-U. S. stocks and bonds, real estate, coins, stamps, art, antiques, and any other marketable risky asset from around the world ® 3/19/20181999 South-Western College Publishing 70

World Market Portfolio • • Include International Securities Steeper CML Less Than Perfect Correlation Objective – Increase the number of assets available – Decrease market portfolio risk • Practical Reasons ® 3/19/20181999 South-Western College Publishing 71

Comparing Market Proxies Calculating Beta for Coca-Cola using Morgan Stanley (M-S) World Equity Index and S&P 500 as market proxies results in a 1. 27 beta when compared with the M-S index, but a 1. 01 beta compared to the S&P 500 The difference is exaggerated by the small sample size (12 months) used, but selecting the market proxy can make a significant difference Here are the computations: ® 3/19/20181999 South-Western College Publishing 72

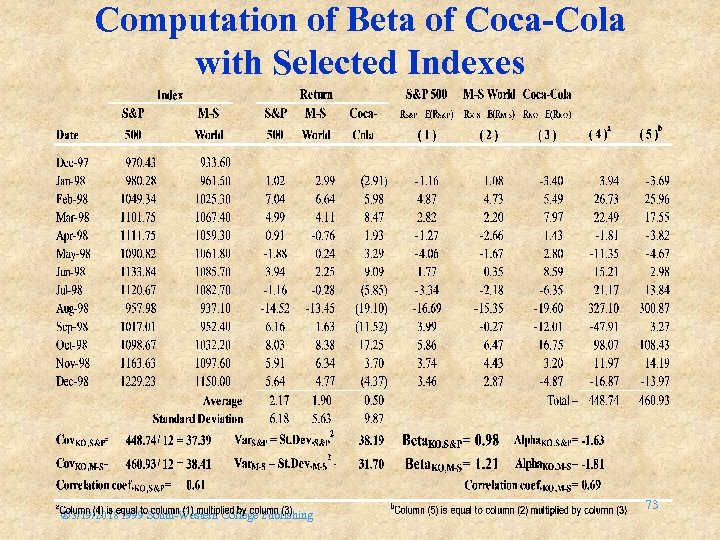Computation of Beta of Coca-Cola with Selected Indexes ® 3/19/20181999 South-Western College Publishing 73

Summary of CAPM Theory • When you combine the risk-free asset with any risky asset on the Markowitz efficient frontier, you derive a set of straight-line portfolio possibilities ® 3/19/20181999 South-Western College Publishing 74

Summary of CAPM Theory • The dominant line is tangent to the efficient frontier – Referred to as the capital market line (CML) – All investors should target points along this line depending on their risk preferences ® 3/19/20181999 South-Western College Publishing 75

Summary of CAPM Theory • All investors want to invest in the risky portfolio, so this market portfolio must contain all risky assets – The investment decision and financing decision can be separated – Everyone wants to invest in the market portfolio – Investors finance based on risk preferences ® 3/19/20181999 South-Western College Publishing 76

Summary of CAPM Theory • The relevant risk measure for an individual risky asset is its systematic risk or covariance with the market portfolio – Once you have determined this Beta measure and a security market line, you can determine the required return on a security based on its systematic risk ® 3/19/20181999 South-Western College Publishing 77

Summary of CAPM Theory • Assuming security markets are not always completely efficient, you can identify undervalued and overvalued securities by comparing your estimate of the rate of return on an investment to its required rate of return ® 3/19/20181999 South-Western College Publishing 78

Summary of CAPM Theory • The Arbitrage Pricing Theory (APT) model makes simpler assumptions, and is more intuitive, but test results are mixed at this point ® 3/19/20181999 South-Western College Publishing 79

Relaxing the Assumptions of the CAPM • CAPM assumption: all investors can borrow or lend at the risk-free rate - unrealistic – Differential borrowing and lending rates – Unlimited lending at risk-free rate – Borrowing at higher rate ® 3/19/20181999 South-Western College Publishing 80

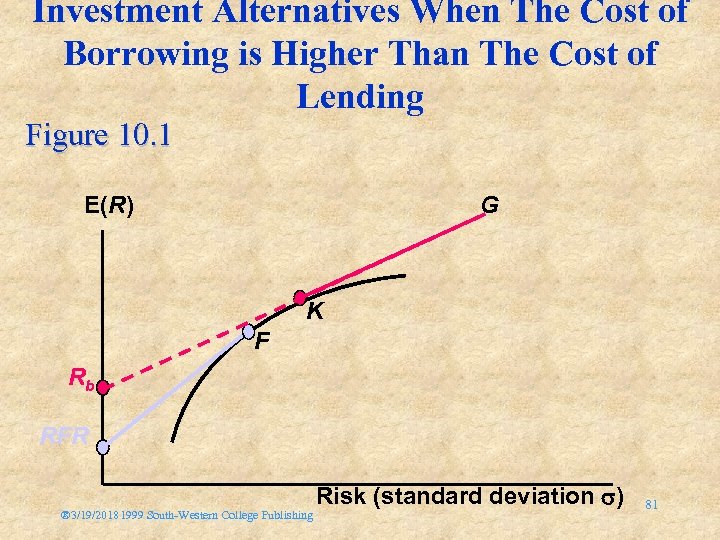Investment Alternatives When The Cost of Borrowing is Higher Than The Cost of Lending Figure 10. 1 E(R) G K F Rb RFR ® 3/19/20181999 South-Western College Publishing Risk (standard deviation ) 81

Relaxing the Assumptions of the CAPM • Zero-beta portfolio: create a portfolio that is uncorrelated to the market (beta 0) – The return of the zero-beta portfolio may differ from the risk-free rate • Any combination of portfolios on the efficient frontier will be on the frontier • Any efficient portfolio will have associated with it a zero-beta portfolio ® 3/19/20181999 South-Western College Publishing 82

Implications of Black’s Zero-beta model • The expected return of any security can be expressed as a linear relationship of any two efficient portfolios E(Ri) = E(Rz) + i[E(Rm) - E(Rz)] • If CAPM defines the relationship between risk and return, then the return on the zero-beta portfolio should equal RF • To test this - identify a market portfolio and solve for the return of a zero-beta portfolio ® 3/19/20181999 South-Western College Publishing 83

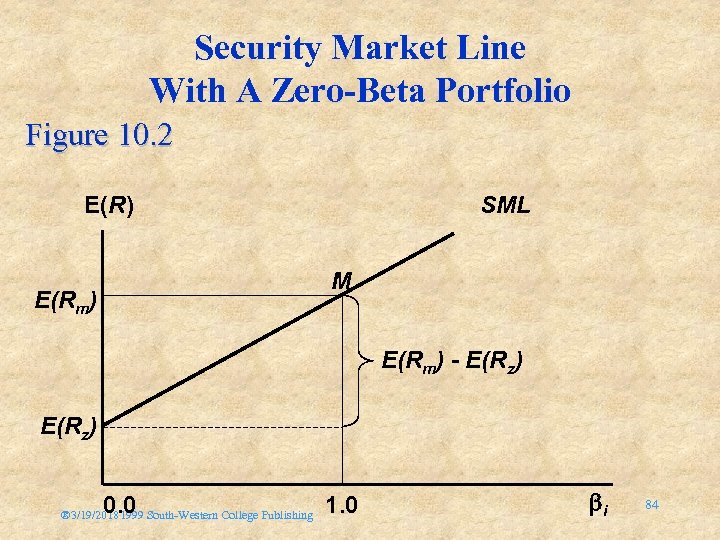Security Market Line With A Zero-Beta Portfolio Figure 10. 2 E(R) SML M E(Rm) - E(Rz) 0. 0 ® 3/19/20181999 South-Western College Publishing 1. 0 i 84

Relaxing the Assumptions of the CAPM • Transaction costs – affect mispricing corrections – affect diversification ® 3/19/20181999 South-Western College Publishing 85

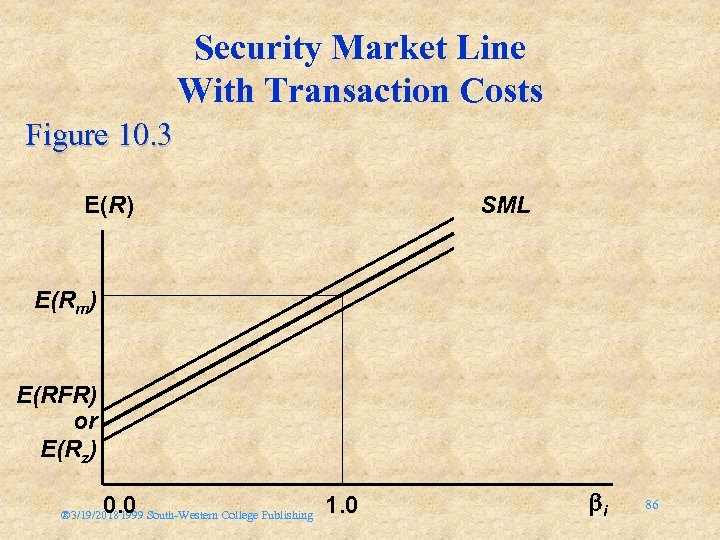Security Market Line With Transaction Costs Figure 10. 3 E(R) SML E(Rm) E(RFR) or E(Rz) 0. 0 ® 3/19/20181999 South-Western College Publishing 1. 0 i 86

Relaxing the Assumptions of the CAPM • Heterogenous expectations – If all investors have different expectations about risk and return, each would have a unique CML and/or SML, and the composite graph would be a band of lines with a breadth determined by the divergence of expectations • Planning periods – CAPM is a one period model, and the period employed should be the planning period for the individual investor, which will vary by individual, affecting both the CML and the SML 87 ® 3/19/20181999 South-Western College Publishing

GCAPM • • “General Capital Asset Pricing Model” Each Investor Holds A Different Portfolio Each Portfolio Has Entails Different ’s Asset’s will be a weighted average of all of the portfolio ’s • Allows Investors to Hold a Relatively Small Number of Assets • Can be used in cases where the above three assumptions (transactions costs, heterogeneous expectations, different planning periods) may not hold 88 ® 3/19/20181999 South-Western College Publishing

Empirical Testing of CAPM • How stable is the measure of systematic risk (beta)? • Is there a positive linear relationship as hypothesized between beta and the rate of return on risky assets? • How well do returns conform to the SML equation? ® 3/19/20181999 South-Western College Publishing 89

Empirical Testing of CAPM • Beta is not stable for individual stocks over short periods of time (52 weeks) • Stability for portfolios increase significantly • The larger the portfolio and the longer the period, the more stable the beta of the portfolio • Betas tend to regress toward the mean ® 3/19/20181999 South-Western College Publishing 90

Empirical Testing of CAPM • Different estimates of beta for a stock vary typically in data used • Value Line estimates use 260 weekly observations • Merrill Lynch estimates using 60 monthly observations • Securities market value affects the size and direction of the interval affect ® 3/19/20181999 South-Western College Publishing 91

Relationship Between Systematic Risk and Return • • Sharpe and Cooper: positive, but non-linear Douglas: intercept higher than the risk-free rate Miller and Scholes: possible error in Douglas findings Black, Jensen, and Scholes: positive linear relationship between monthly excess return and portfolio beta • Fama and Mc. Beth: supported the CAPM with the intercept equal to the RFR ® 3/19/20181999 South-Western College Publishing 92

Relationship Between Systematic Risk and Return • Effect of skewness on the relationship – preference for high risk and returns • Effect of size, P/E and leverage • Effect of book-to-market value – The Fama-French Study ® 3/19/20181999 South-Western College Publishing 93

Shortcomings Of CAPM • is Dead • is Alive, but not well ® 3/19/20181999 South-Western College Publishing 94

The Market Portfolio: Theory Versus Practice • Difficult to test full market • Portfolio used as market proxy may be correlated to true market portfolio • Benchmark error ® 3/19/20181999 South-Western College Publishing 95

Criticism of CAPM by Richard Roll • Limits on tests: only testable implication from CAPM is whether the market portfolio lies on the efficient frontier • Range of SML’s - infinite number of possible SML’s, each of which produces a unique estimate of beta ® 3/19/20181999 South-Western College Publishing 96

Criticism of CAPM by Richard Roll • Market efficiency effects - substituting a proxy, such as the S&P 500 creates two problems – Proxy does not represent the true market portfolio – Even if the proxy is not efficient, the market portfolio might be ® 3/19/20181999 South-Western College Publishing 97

Criticism of CAPM by Richard Roll • Conflicts between proxies - different substitutes may be highly correlated even though some may be efficient and others are not, which can lead to different conclusions regarding beta risk/return relationships • So, CAPM is not testable - but it still has value and must be used carefully • Stephen Ross devised an alternative way to look at asset pricing - APT ® 3/19/20181999 South-Western College Publishing 98