Chapter 9 Estimation Using a Single Sample

Chapter 9 Estimation Using a Single Sample

Point Estimation A point estimate of a population characteristic is a single number that is based on sample data and represents a plausible value of the characteristic. 2

Example A sample of 200 students at a large university is selected to estimate the proportion of students that wear contact lens. In this sample 47 wear contact lens. Let p = the true proportion of all students at this university that wear contact lens. Consider “success” being a student wears contact lens. 3

Example A sample of weights of 34 male freshman students was obtained. 185 170 188 184 161 151 170 179 174 176 207 155 175 197 180 148 202 214 167 180 178 283 177 194 202 184 166 176 139 189 231 177 168 176 If one wanted to estimate the true mean of all male freshman students, you might use the sample mean as a point estimate for the true mean. 4

Example After looking at a histogram and boxplot of the data (below) you might notice that the data seems reasonably symmetric with a outlier, so you might use either the sample median or a sample trimmed mean as a point estimate. 140 5 180 220 260

Bias A statistic with mean value equal to the value of the population characteristic being estimated is said to be an unbiased statistic. A statistic that is not unbiased is said to be biased. 6

Criteria Given a choice between several unbiased statistics that could be used for estimating a population characteristic, the best statistic to use is the one with the smallest standard deviation. 7

Large-sample Confidence Interval for a Population Proportion A confidence interval for a population characteristic is an interval of plausible values for the characteristic. It is constructed so that, with a chosen degree of confidence, the value of the characteristic will be captured inside the interval. 8

Confidence Level The confidence level associated with a confidence interval estimate is the success rate of the method used to construct the interval. 9

Recall 10

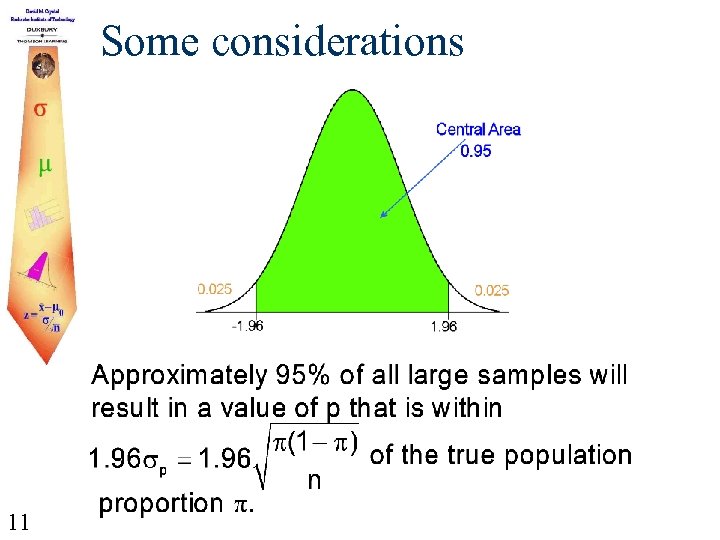Some considerations 11

Some considerations 12

The 95% Confidence Interval 13

Example For a project, a student randomly sampled 182 other students at a large university to determine if the majority of students were in favor of a proposal to build a field house. He found that 75 were in favor of the proposal. Let p = the true proportion of students that favor the proposal. 14

Example - continued 15

The General Confidence Interval The general formula for a confidence interval for a population proportion p when 1. p is the sample proportion from a random sample , and 2. The sample size n is large (np 10 and np(1 -p) 10) is 16

Finding a z Critical Value Finding a z critical value for a 98% confidence interval. 2. 33 17 Looking up the cumulative area or 0. 9900 in the body of the table we find z = 2. 33

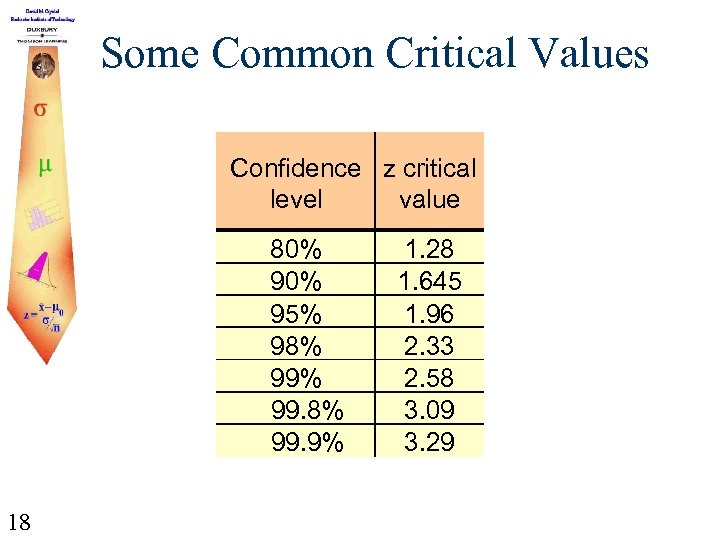Some Common Critical Values Confidence z critical level value 80% 95% 98% 99. 9% 18 1. 28 1. 645 1. 96 2. 33 2. 58 3. 09 3. 29

Terminology 19

Terminology The bound on error of estimation, B, associated with a 95% confidence interval is (1. 96) (standard error of the statistic). The bound on error of estimation, B, associated with a confidence interval is (z critical value)·(standard error of the statistic). 20

Sample Size The sample size required to estimate a population proportion p to within an amount B with 95% confidence is The value of p may be estimated by prior information. If no prior information is available, use p = 0. 5 in the formula to obtain a conservatively large value for n. Generally one rounds the result up to the nearest integer. 21

Sample Size Calculation Example If a TV executive would like to find a 95% confidence interval estimate within 0. 03 for the proportion of all households that watch NYPD Blue regularly. How large a sample is needed if a prior estimate for p was 0. 15. We have B = 0. 03 and the prior estimate of p = 0. 15 A sample of 545 or more would be needed. 22

Sample Size Calculation Example revisited Suppose a TV executive would like to find a 95% confidence interval estimate within 0. 03 for the proportion of all households that watch NYPD Blue regularly. How large a sample is needed if we have no reasonable prior estimate for p. We have B = 0. 03 and should use p = 0. 5 in the formula. 23 The required sample size is now 1068. Notice, a reasonable ball park estimate for p can lower the needed sample size.

Another Example A college professor wants to estimate the proportion of students at a large university who favor building a field house with a 99% confidence interval accurate to 0. 02. If one of his students performed a preliminary study and estimated p to be 0. 412, how large a sample should he take. We have B = 0. 02, a prior estimate p = 0. 412 and we should use the z critical value 2. 58 (for a 99% confidence interval) 24 The required sample size is 4032.

One-Sample z Confidence Interval for m 25

One-Sample z Confidence Interval for m If n is small (generally n < 30) but it is reasonable to believe that the distribution of values in the population is normal, a confidence interval for m (when is known) is Notice that this formula works when is known and either 1. n is large (generally n 30) or 26 2. The population distribution is normal (any sample size.

Example Find a 90% confidence interval estimate for the true mean fills of catsup from this machine. 27

Example I (continued) x = 6. 018, = 0. 228, n = 36 Z critical value is 1. 645 90% Confidence Interval 28 (5. 955, 6. 081) 1. 645

Unknown - Small Size Samples [All Size Samples] 29

t Distributions 30

t Distributions 31

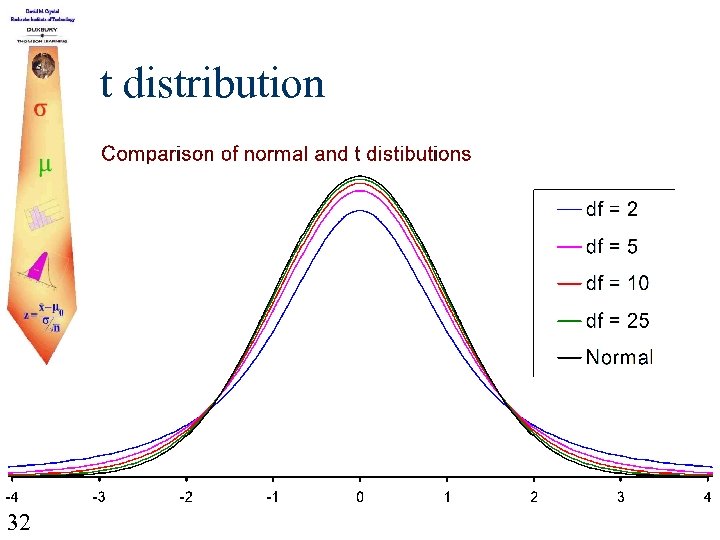t distribution 32

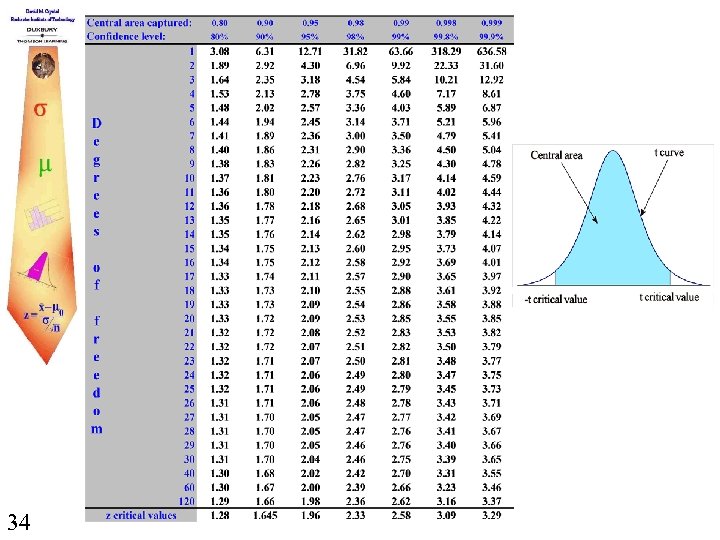
t Distributions Continued Notice: As df increase, t distributions approach the standard normal distribution. Since each t distribution would require a table similar to the standard normal table, we usually only create a table of critical values for the t distributions. 33

34

One-Sample t Procedures 35

Confidence Interval Example Ten randomly selected shut-ins were each asked to list how many hours of television they watched per week. The results are 82 66 90 84 75 88 80 94 110 91 Find a 90% confidence interval estimate for the true mean number of hours of television watched per week by shut-ins. 36

Confidence Interval Example Continued 37

Confidence Interval Example Continued To calculate the confidence interval, we had to make the assumption that the distribution of weekly viewing times was normally distributed. Consider the following normal plot of the 10 data points. 38

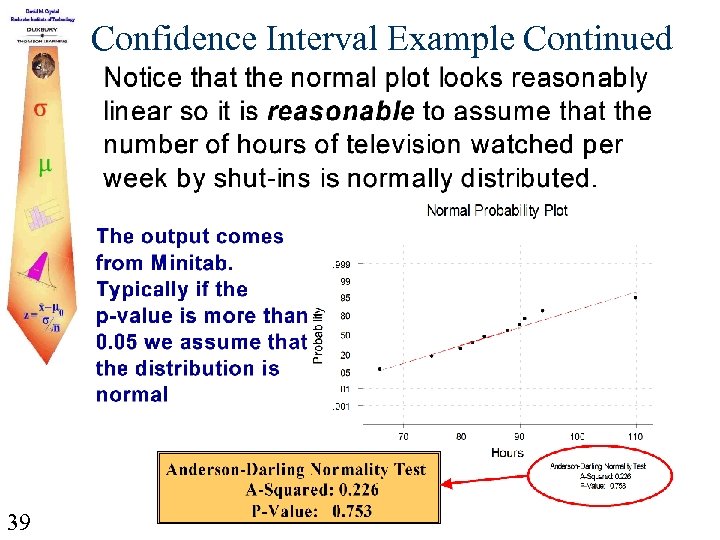Confidence Interval Example Continued 39