23976b4010a3e8e1c58f5196c4013953.ppt
- Количество слайдов: 25

Chapter 8 Sampling Variability and Sampling Distributions

Basic Terms Any quantity computed from values in a sample is called a statistic. The observed value of a statistic depends on the particular sample selected from the population; typically, it varies from sample to sample. This variability is called sampling variability. 2

Sampling Distribution The distribution of a statistic is called its sampling distribution. 3

Example Consider a population that consists of the numbers 1, 2, 3, 4 and 5 generated in a manner that the probability of each of those values is 0. 2 no matter what the previous selections were. This population could be described as the outcome associated with a spinner such as given below with the distribution next to it. 4

Example If the sampling distribution for the means of samples of size two is analyzed, it looks like 5
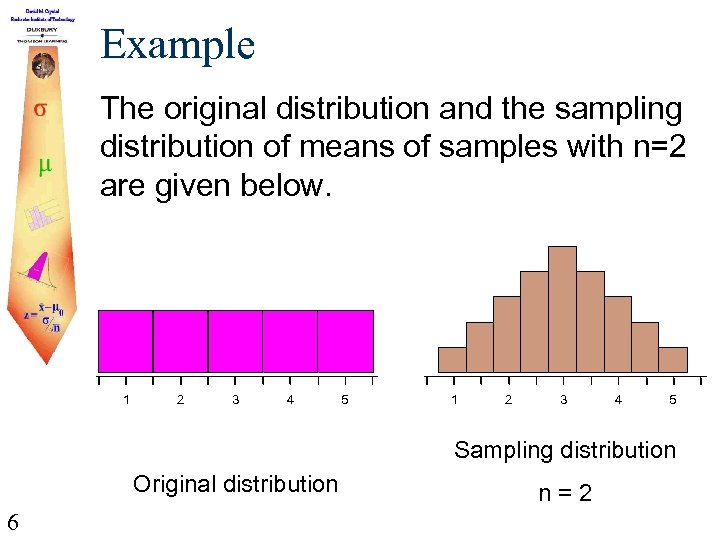
Example The original distribution and the sampling distribution of means of samples with n=2 are given below. 1 2 3 4 5 Sampling distribution Original distribution 6 n=2
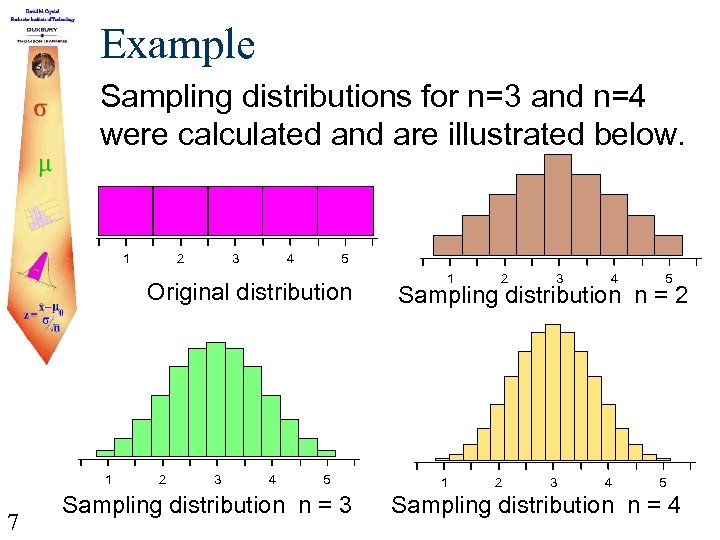
Example Sampling distributions for n=3 and n=4 were calculated and are illustrated below. 1 2 3 4 5 Original distribution 1 7 2 3 4 5 Sampling distribution n = 3 1 2 3 4 5 Sampling distribution n = 2 1 2 3 4 5 Sampling distribution n = 4
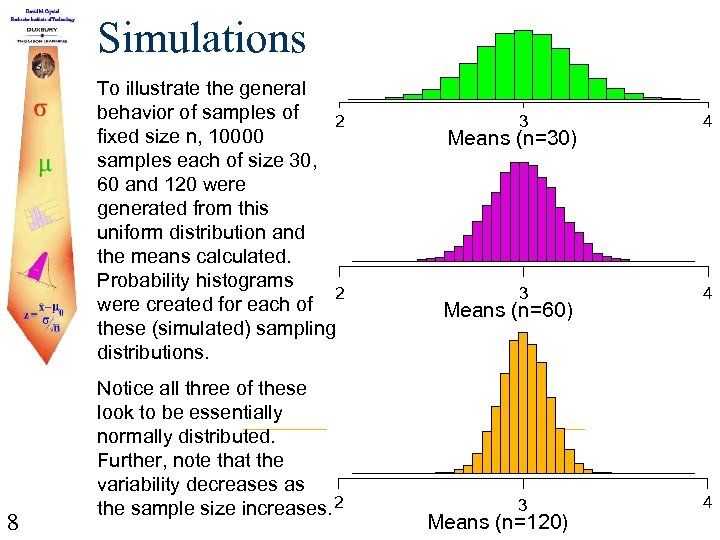
Simulations To illustrate the general behavior of samples of 2 fixed size n, 10000 samples each of size 30, 60 and 120 were generated from this uniform distribution and the means calculated. Probability histograms 2 were created for each of these (simulated) sampling distributions. 8 Notice all three of these look to be essentially normally distributed. Further, note that the variability decreases as the sample size increases. 2 3 4 3 4 Means (n=30) Means (n=60) Means (n=120)
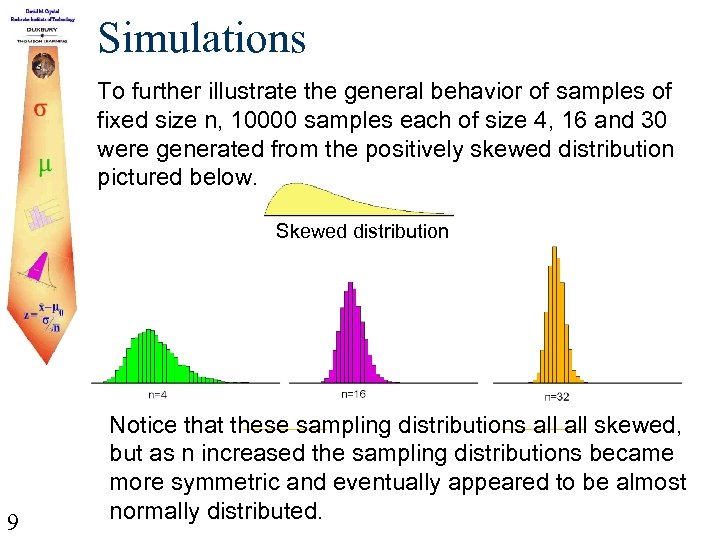
Simulations To further illustrate the general behavior of samples of fixed size n, 10000 samples each of size 4, 16 and 30 were generated from the positively skewed distribution pictured below. Skewed distribution 9 Notice that these sampling distributions all skewed, but as n increased the sampling distributions became more symmetric and eventually appeared to be almost normally distributed.

Terminology Let denote the mean of the observations in a random sample of size n from a population having mean m and standard deviation s. Denote the mean value of the distribution by and the standard deviation of the distribution by (called the standard error of the mean), then the rules on the next two slides hold. 10

Properties of the Sampling Distribution of the Sample Mean. 11

Central Limit Theorem. Rule 4: When n is sufficiently large, the sampling distribution of is approximately normally distributed, even when the population distribution is not itself normal. 12
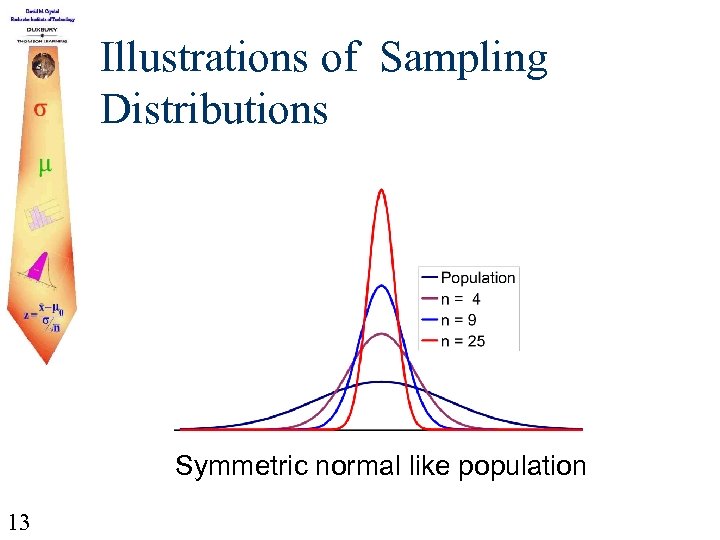
Illustrations of Sampling Distributions Symmetric normal like population 13
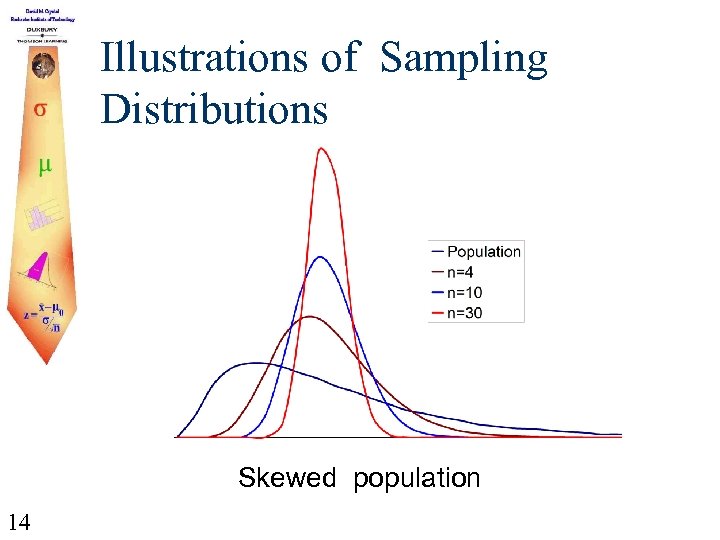
Illustrations of Sampling Distributions Skewed population 14

More about the Central Limit Theorem. The Central Limit Theorem can safely be applied when n exceeds 30. If n is large or the population distribution is normal, the standardized variable 15 has (approximately) a standard normal (z) distribution.

Example A food company sells “ 18 ounce” boxes of cereal. Let x denote the actual amount of cereal in a box of cereal. Suppose that x is normally distributed with m = 18. 03 ounces and s = 0. 05. a) What proportion of the boxes will contain less than 18 ounces? 16

Example - continued b) A case consists of 24 boxes of cereal. What is the probability that the mean amount of cereal (per box in a case) is less than 18 ounces? The central limit theorem states that the distribution of is normally distributed so 17
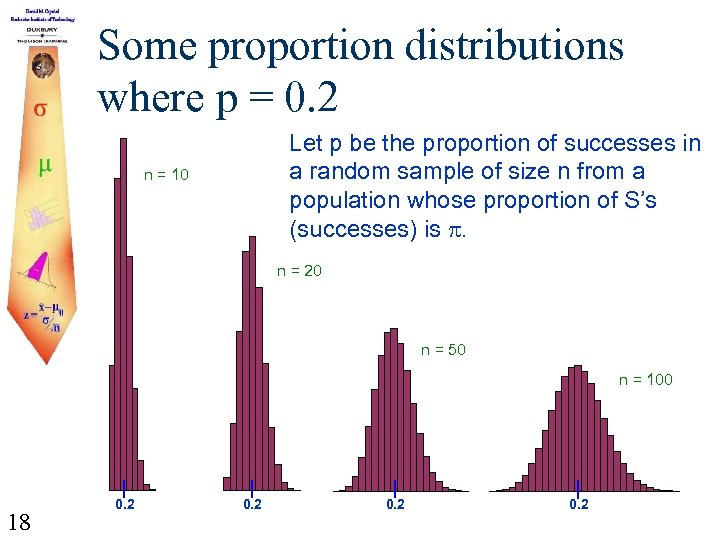
Some proportion distributions where p = 0. 2 Let p be the proportion of successes in a random sample of size n from a population whose proportion of S’s (successes) is p. n = 10 n = 20 n = 50 n = 100 18 0. 2

Properties of the Sampling Distribution of p Let p be the proportion of successes in a random sample of size n from a population whose proportion of S’s (successes) is p. Denote the mean of p by mp and the standard deviation by sp. Then the following rules hold 19

Properties of the Sampling Distribution of p Rule 1: Rule 2: Rule 3: When n is large and p is not too near 0 or 1, the sampling distribution of p is approximately normal. 20

Condition for Use The further the value of p is from 0. 5, the larger n must be for a normal approximation to the sampling distribution of p to be accurate. Rule of Thumb If both np 10 and n(1 -p) 10, then it is safe to use a normal approximation. 21

Example If the true proportion of defectives produced by a certain manufacturing process is 0. 08 and a sample of 400 is chosen, what is the probability that the proportion of defectives in the sample is greater than 0. 10? Since np = 400(0. 08) = 32 > 10 and n(1 -p) = 400(0. 92) = 368 > 10, it’s reasonable to use the normal approximation. 22
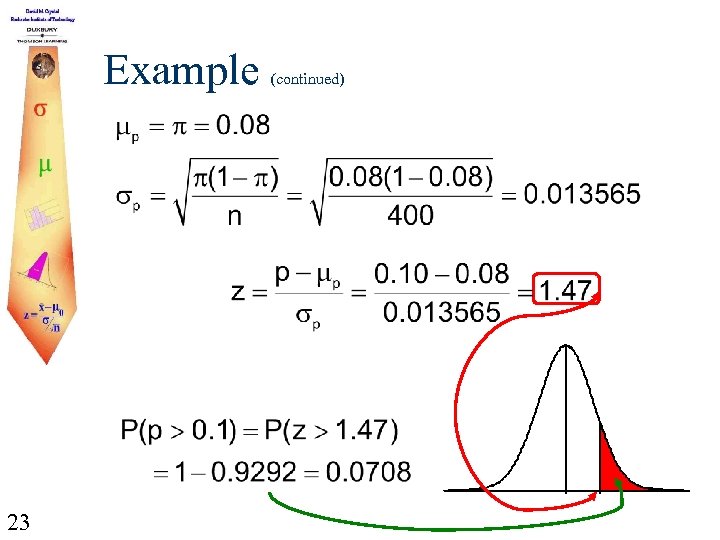
Example 23 (continued)

Example Suppose 3% of the people contacted by phone are receptive to a certain sales pitch and buy your product. If your sales staff contacts 2000 people, what is the probability that more than 100 of the people contacted will purchase your product? Clearly p = 0. 03 and p = 100/2000 = 0. 05 so 24

Example - continued If your sales staff contacts 2000 people, what is the probability that less than 50 of the people contacted will purchase your product? Now p = 0. 03 and p = 50/2000 = 0. 025 so 25
23976b4010a3e8e1c58f5196c4013953.ppt