CHAPTER 8 Large-Sample Estimation Copyright 2011 Nelson

CHAPTER 8 Large-Sample Estimation Copyright © 2011 Nelson Education Limited

Key Concepts I. Types of Estimators 1. Point estimator: a single number is calculated to estimate the population parameter. 2. Interval estimator: two numbers are calculated to estimator form an interval that contains the parameter. Copyright © 2011 Nelson Education Limited

Key Concepts II. Properties of Good Estimators 1. Unbiased: the average value of the estimator equals the parameter to be estimated. 2. Minimum variance: of all the unbiased estimators, the best estimator has a sampling distribution with the smallest standard error. 3. The margin of error measures the maximum distance between the estimator and the true value of the parameter. THIS CHAPTER – SAMPLE SIZE IS LARGE ENOUGH TO USE CLT!! Copyright © 2011 Nelson Education Limited

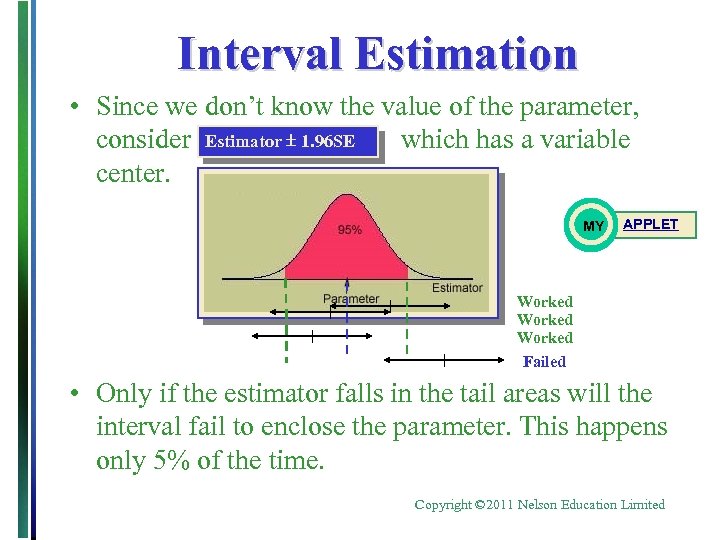Interval Estimation • Since we don’t know the value of the parameter, consider Estimator 1. 96 SE which has a variable center. MY APPLET Worked Failed • Only if the estimator falls in the tail areas will the interval fail to enclose the parameter. This happens only 5% of the time. Copyright © 2011 Nelson Education Limited

Confidence Intervals: Estimator +/- 1. 96 SE Copyright © 2011 Nelson Education Limited

Example • Of a random sample of n = 150 college students, 104 of the students said that they had played on a soccer team during their K-12 years. Estimate the proportion of college students who played soccer in their youth with a 98% confidence interval. Copyright © 2011 Nelson Education Limited

Estimating the Difference between Two Means • Sometimes we are interested in comparing the means of two populations. • The average growth of plants fed using two different nutrients. • The average scores for students taught with two different teaching methods. • To make this comparison, Copyright © 2011 Nelson Education Limited

Estimating the Difference between Two Means • We compare the two averages by making inferences about m 1 -m 2, the difference in the two population averages. • If the two population averages are the same, then m 1 -m 2 = 0. • The best estimate of m 1 -m 2 is the difference in the two sample means, Copyright © 2011 Nelson Education Limited

Sampling Distribution of Copyright © 2011 Nelson Education Limited

Estimating m 1 -m 2 • For large samples (n 1, n 2 >=30), point estimates and their margin of error as well as confidence intervals are based on the standard normal (z) distribution. Copyright © 2011 Nelson Education Limited

Example Avg Daily Intakes Men Women Sample size 50 50 Sample mean 756 762 Sample Std Dev 35 30 • Compare the average daily intake of dairy products of men and women using a 95% confidence interval. Copyright © 2011 Nelson Education Limited

Example, continued Confidence interval for mean difference: (-18, 78, 6. 78) • Could you conclude, based on this confidence interval, that there is a difference in the average daily intake of dairy products for men and women? • The confidence interval contains the value m 1 -m 2= 0. Therefore, it is possible that m 1 = m 2. You would not want to conclude that there is a difference in average daily intake of dairy products for men and women. Copyright © 2011 Nelson Education Limited

Estimating the Difference between Two Proportions • Sometimes we are interested in comparing the proportion of “successes” in two binomial populations. • The germination rates of untreated seeds and seeds treated with a fungicide. • The proportion of male and female voters who favor a particular candidate for prime minister. • To make this comparison, The two samples are independent! Copyright © 2011 Nelson Education Limited

Estimating the Difference between Two Means • We compare the two proportions by making inferences about p 1 -p 2, the difference in the two population proportions. • If the two population proportions are the same, then p 1 -p 2 = 0. • The best estimate of p 1 -p 2 is the difference in the two sample proportions, Copyright © 2011 Nelson Education Limited

The Sampling Distribution of Copyright © 2011 Nelson Education Limited

Estimating p 1 -p 2 • For large samples, point estimates and their margin of error as well as confidence intervals are based on the standard normal (z) distribution. Copyright © 2011 Nelson Education Limited

Example Youth Soccer Male Female Sample size 80 70 Played soccer 65 39 • Compare the proportion of male and female university students who said that they had played on a soccer team during their K-12 years using a 99% confidence interval. Copyright © 2011 Nelson Education Limited

Example, continued Confidence interval: (0. 06, 0. 44) • Could you conclude, based on this confidence interval, that there is a difference in the proportion of male and female university students who said that they had played on a soccer team during their K-12 years? • The confidence interval does not contains the value p 1 -p 2 = 0. Therefore, it is not likely that p 1= p 2. You would conclude that there is a difference in the proportions for males and females. Copyright © 2011 Nelson Education Limited

Choosing the Sample Size • The total amount of relevant information in a sample is controlled by two factors: - The sampling plan or experimental design: the design procedure for collecting the information - The sample size n: the amount of information you collect. • In a statistical estimation problem, the accuracy of the estimation is measured by the margin of error or the width of the confidence interval. Copyright © 2011 Nelson Education Limited

Choosing the Sample Size 1. Determine the size of the margin of error, B, that you are willing to tolerate. 2. Choose the sample size by solving for n = n 1 = n 2 in the inequality: 1. 96 SE £ B, where SE is a function of the sample size n. 3. For quantitative populations, estimate the population standard deviation using a previously calculated value of s or the range approximation s » Range / 4. 4. For binomial populations, use the conservative approach and approximate p using the value p =. 5. . 5 Copyright © 2011 Nelson Education Limited

Example A producer of PVC pipe wants to survey wholesalers who buy his product in order to estimate the proportion who plan to increase their purchases next year. What sample size is required if he wants his estimate to be within. 04 of the actual proportion with probability equal to. 95? Copyright © 2011 Nelson Education Limited

Key Concepts III. Large-Sample Point Estimators To estimate one of four population parameters when the sample sizes are large, use the following point estimators with the appropriate margins of error. Copyright © 2011 Nelson Education Limited

Key Concepts IV. Large-Sample Interval Estimators To estimate one of four population parameters when the sample sizes are large, use the following interval estimators. Copyright © 2011 Nelson Education Limited