e726c8de3ca7f7df6e5eb6ba5d26c070.ppt
- Количество слайдов: 40

Chapter 8 Indicator Variable Ray-Bing Chen Institute of Statistics National University of Kaohsiung 1

8. 1 The General Concept of Indicator Variables • The Variables in regression analysis: – Quantitative variables: well-defined scale of measurement. For example: temperature, distance, income, … – Qualitative variable (Categorical variable): for example: operators, employment status (employed or unemployed), shifts (day, evening or night), and sex (male or female). Usually no natural scale of measurement. 2

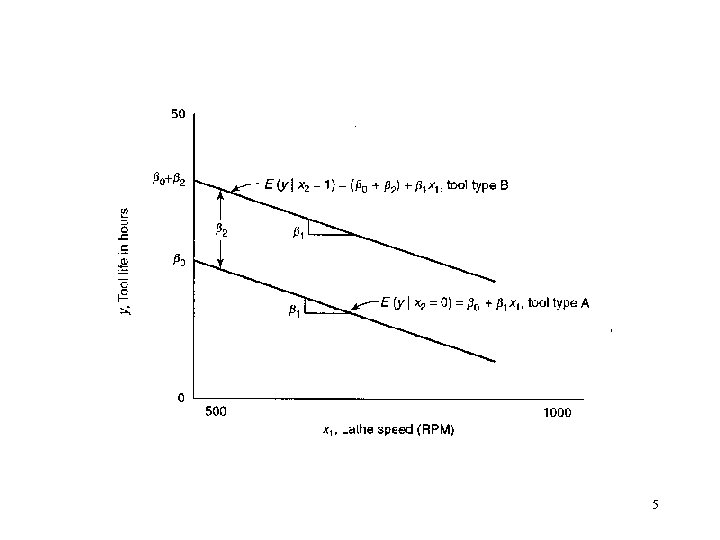
• Assign a set of levels to a qualitative variable to account the effect that variable may have on the response. (indicator variable or dummy variable) • For example: The effective life of a cutting tool (y) v. s. the lathe speed (x 1) and the type of cutting tool (x 2). 3

4
5

6

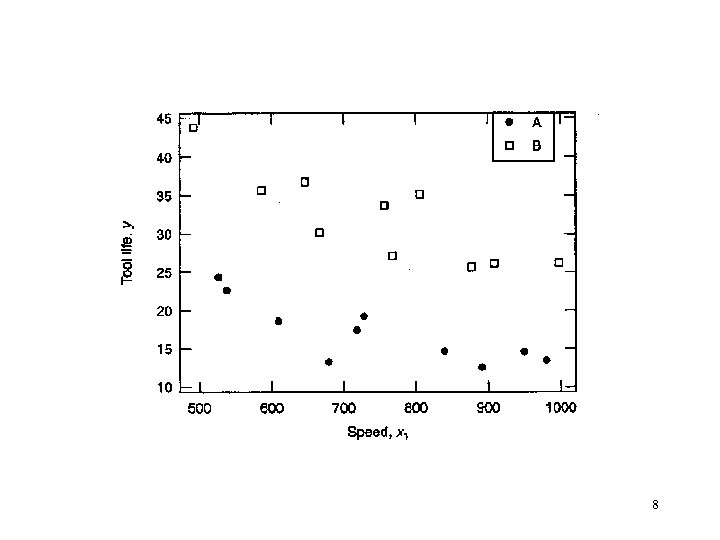
Example 8. 1 Tool Life Data • The scatter diagram is in Figure 8. 2. • Two different regression lines. 7
8

9
10
11

• Two separate straight-line models v. s. a single model with an indicator variable: – Prefer the single-model approach (a simpler practical result) – Since assume the same slope, it makes sense to combine the data from both tool types to produce a single estimate of this common parameter. – Can give one estimate of the common error variance 2 and more residual degrees of freedom. 12

• Different in intercept and slope: 13

14

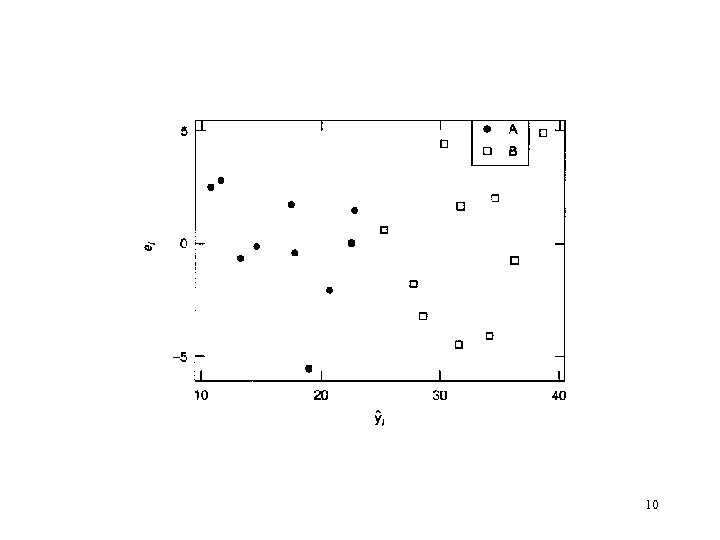
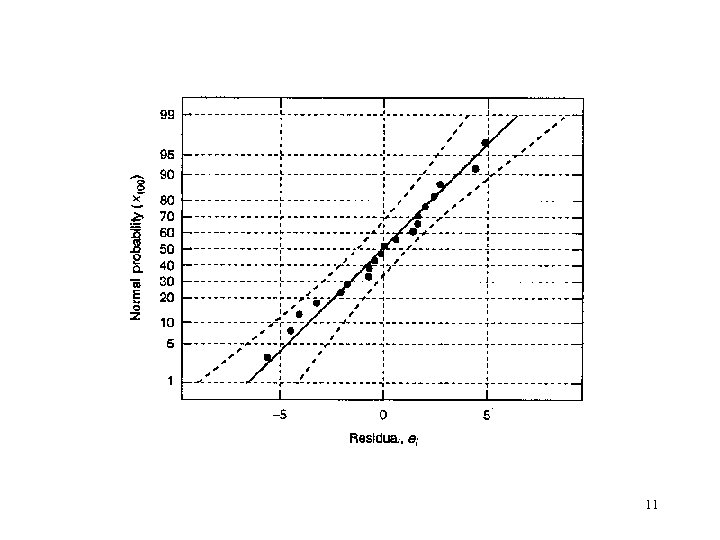
Example 8. 2 The Tool Life Data: 15

16

17

Example 8. 3 An Indicator Variable with More Than Two Levels • Total electricity consumption (y) v. s. the size of house (x 1) and the four types of sir condition systems. • Four types of air conditions systems: 18

• 3 - 4: relative efficiency of a heat pump compared to central air conditioning. • Assume the variance doesn’t depend on the types. 19

20

Example 8. 4 More Than One Indicator Variable • Add the type of cutting oil used in Example 8. 1 • 21

22

23

24

25

26

8. 2 Comments on the Use of Indicator Variables 8. 2. 1 Indicator Variables versus Regression on Allocated Codes • Another approach to measure the levels of the variables is by an allocated code. • In Example 8. 3, 27

28

• The allocated codes impose a particular metric on the levels of the qualitative factor. • Indicator variables are more informative because they do not force any particular metric on the levels of the qualitative factor. • Searle and Udell (1970): regression using indicator variables always leads to a larger R 2 than does regression on allocated codes. 29

8. 2. 2 Indicator Variables as a Substitute for a Quantitative Regressor • Quantitative regressor can also be represented by indicator variables. • In Example 8. 3, for income factor: • Use four indicator variables to represent the factor “income”. 30

• Disadvantage: – More parameters are required to represent the information content of the quantitative factor. (a -1 v. s. 1) So it would increase the complexity of the model. – Reduce the degrees of freedom for error. • Advantage: It does not require the analyst to make any prior assumptions about the functional form of the relationship between the response and the regressor variable. 31

8. 3 Regression Approach to Analysis of Variance • The Analysis of Variance is a technique frequently used to analyze data from planned ot designed experiments. • Any ANOVA problem can be treated as a linear regression problem. • Ordinarily we do not recommend that regression mothods be used for ANOVA because the specialized computing techniques are usually quite efficient. 32

• However, there some ANOVA situation, particularly those involving unbalance designs, where the regression approach is helpful. • Essentially, any ANOVA problem can be treated as a regression problem in which all of the regressors are indicator variables. n 33

• Define the treatment effects in the balance case (an equal number of observations per treatment) as 1 + 2 + … + k = n • i = + i is the mean of the ith treatment. • Test H 0 : 1 = 2 = … = k = 0 v. s. H 1 : 2 0 for at least one i 34

35

Example: 3 treatments • Model: yij = + ij , i = 1, 2, 3, j = 1, 2, …, n 36
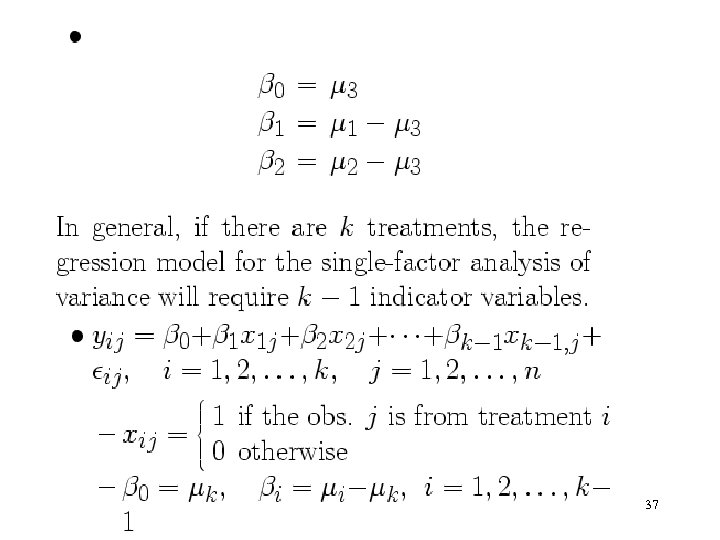
37
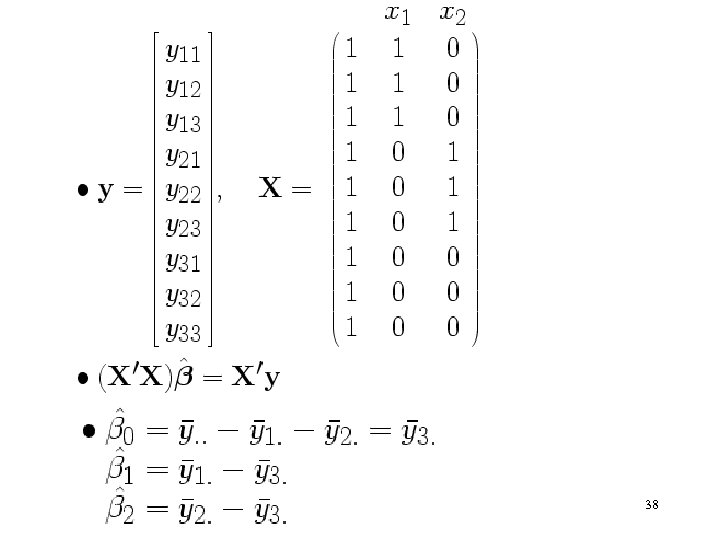
38
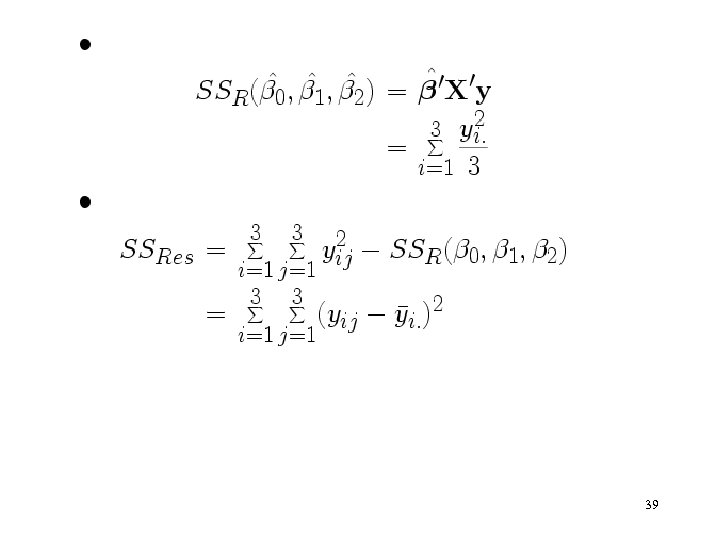
39

40
e726c8de3ca7f7df6e5eb6ba5d26c070.ppt