Chapter 8 Graph Algorithms July 23 2012 Name Xuanyu Hu

Chapter 8: Graph Algorithms July/23/2012 Name: Xuanyu Hu Professor: Elise de Doncker

Outline • • Graphs and Genetics DNA Sequencing Shortest Superstring Problem

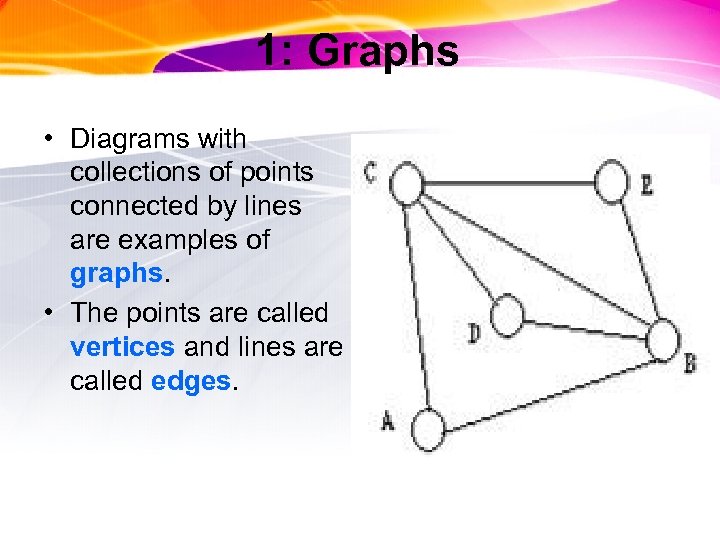1: Graphs • Diagrams with collections of points connected by lines are examples of graphs. • The points are called vertices and lines are called edges.

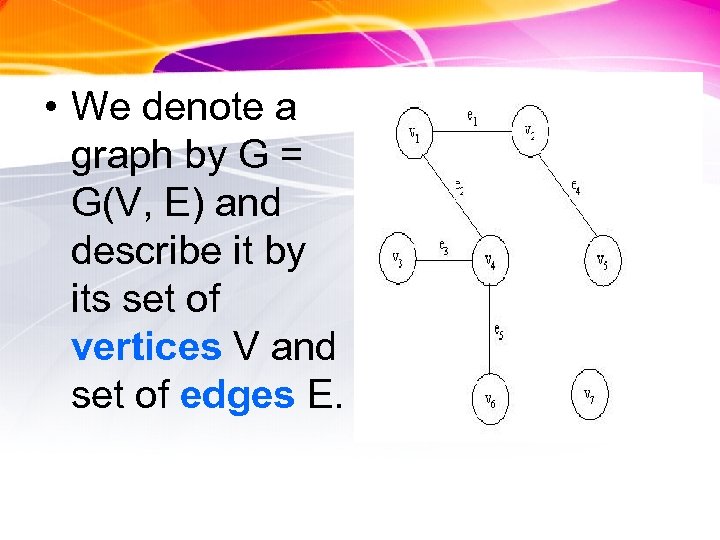• We denote a graph by G = G(V, E) and describe it by its set of vertices V and set of edges E.

How to Use Graph: Knights Problem 1 • This upper picture shows two white and two black knights on a 3*3 chessboard. • Can they move, using the usual chess knight's moves, to occupy the positions shown in the below picture?

• This picture represents the chessboard as a set of nine points. • Two points are connected by a line if moving from one point to another is a valid knight move.

• The upper picture represents the chessboard as a set of nine points. • Two points are connected by a line if moving from one point to another is a valid knight move.

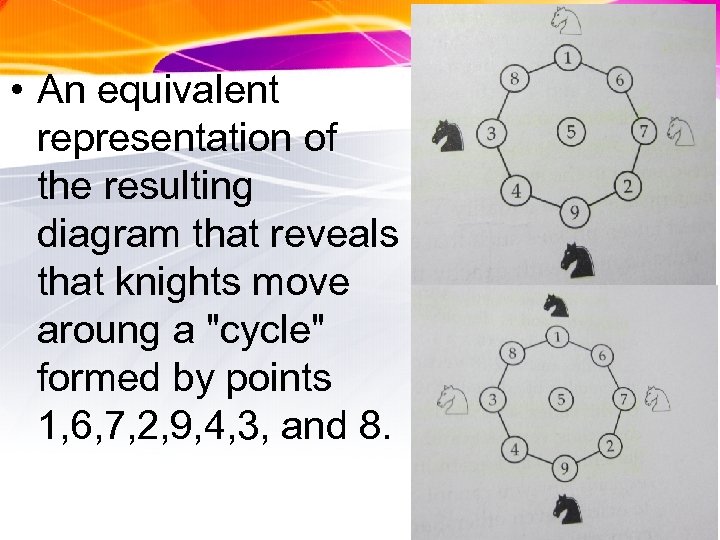• An equivalent representation of the resulting diagram that reveals that knights move aroung a "cycle" formed by points 1, 6, 7, 2, 9, 4, 3, and 8.

• Every knight's move on the chessboard corresponds to moving to a neighboring point in the diagram, in either a clockwise or counterclockwise direction. • Therefore, the white-whiteblack-black knight arrangement cannot be transformed into the alternating white-black-whiteblack arrangement.

How to Use Graph: Knights Problem 2 • This picture represents anohter chessboard obtained from a 4*4 chessboard by removing the four corner squares. • Can a knight travel around this board, pass through each square exactly once, and return to the same square it started on?

• A rather complex graph with twelve vertices and sixteen edges revealing all possible knight moves.

• Rearranging the vertices reveals the cycle that describes the correct sequence of moves.

Connected and Disconnected • A graph is called connected if all pairs of vertices can be connected by a path, which is a continuous sequence of edges, where each successive edge begins where the previous one left off. • Graphs that are not connected are disconnected.

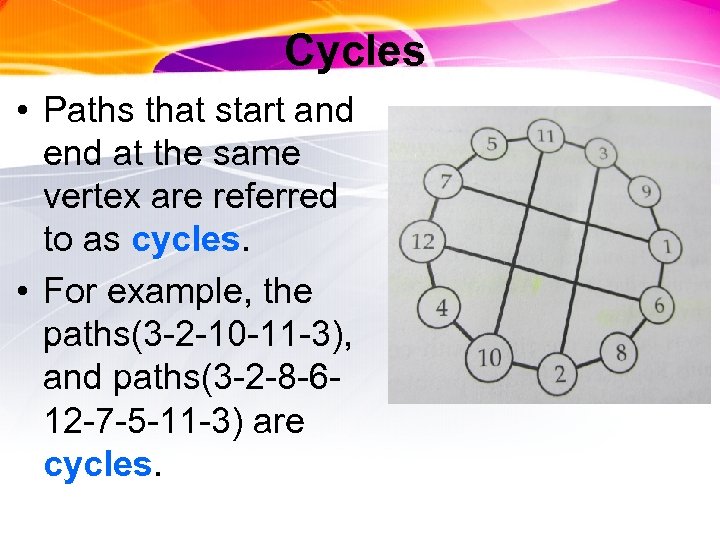Cycles • Paths that start and end at the same vertex are referred to as cycles. • For example, the paths(3 -2 -10 -11 -3), and paths(3 -2 -8 -612 -7 -5 -11 -3) are cycles.

The Bridge Obsession Problem Find a tour crossing every bridge just once Leonhard Euler, 1735 Bridges of Königsberg

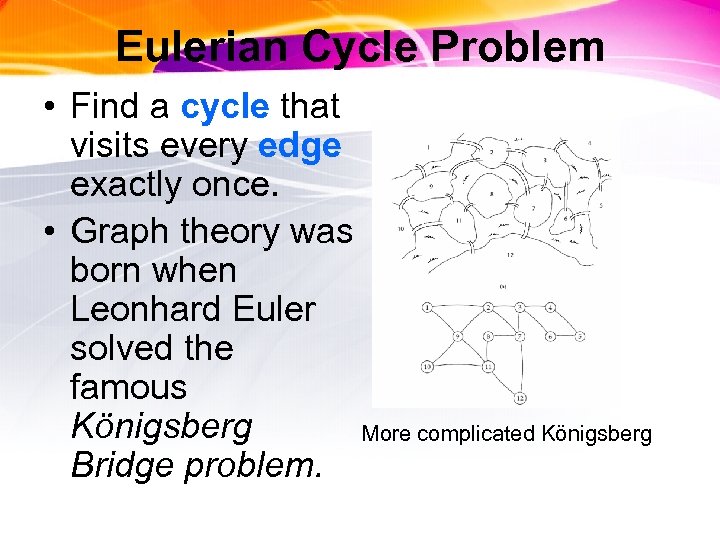Eulerian Cycle Problem • Find a cycle that visits every edge exactly once. • Graph theory was born when Leonhard Euler solved the famous Königsberg More complicated Königsberg Bridge problem.

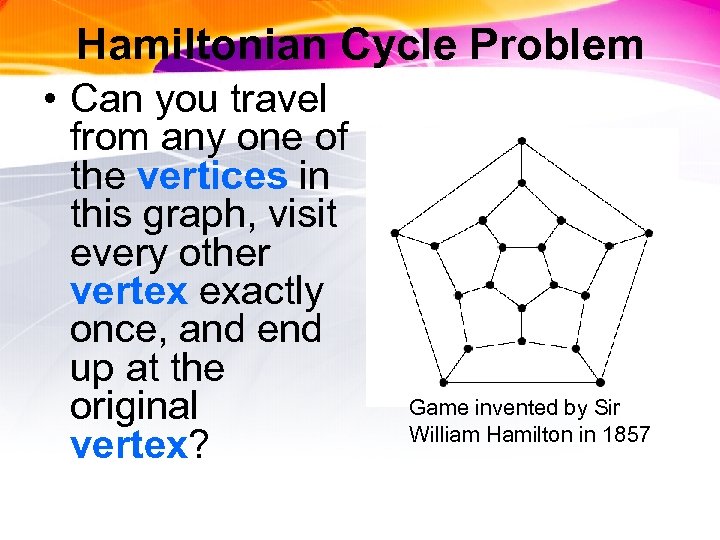Hamiltonian Cycle Problem • Can you travel from any one of the vertices in this graph, visit every other vertex exactly once, and end up at the original vertex? Game invented by Sir William Hamilton in 1857

Trees • Arthur Cayley studied chemical structures of hydrocarbons in the mid -1800 s • Structures of this type of hydrocarbon are examples of trees, which are simply connected graphs with no cycles.

• Every tree has at least one vertex with degree 1, called leaf. • Every tree on n vertices has n-1 edges, regardless of the structure of the tree.

• Every tree on n vertices has n-1 edges, regardless of the structure of the tree. • Every tree has a leaf, we can remove it and its attached edge. We keep this up until we are left with a graph with a single vertex and no edges.

2: Graphs and Genetics Benzer’s work • Developed deletion mapping • “Proved” linearity of the gene • Demonstrated internal structure of the gene Seymour Benzer, 1950 s

Viruses Attack Bacteria • Normally bacteriophage T 4 kills bacteria • However if T 4 is mutated (e. g. , an important gene is deleted) it gets disable and looses an ability to kill bacteria • Suppose the bacteria is infected with two different mutants each of which is disabled – would the bacteria still survive? • Amazingly, a pair of disable viruses can kill a bacteria even if each of them is disabled. • How can it be explained?

Benzer’s Experiment • Idea: infect bacteria with pairs of mutant T 4 bacteriophage (virus) • Each T 4 mutant has an unknown interval deleted from its genome • If the two intervals overlap: T 4 pair is missing part of its genome and is disabled – bacteria survive • If the two intervals do not overlap: T 4 pair has its entire genome and is enabled – bacteria die

Benzer’s Experiment and Graphs • Construct an interval graph: each T 4 mutant is a vertex, place an edge between mutant pairs where bacteria survived (i. e. , the deleted intervals in the pair of mutants overlap) • Interval graph structure reveals whether DNA is linear or branched DNA

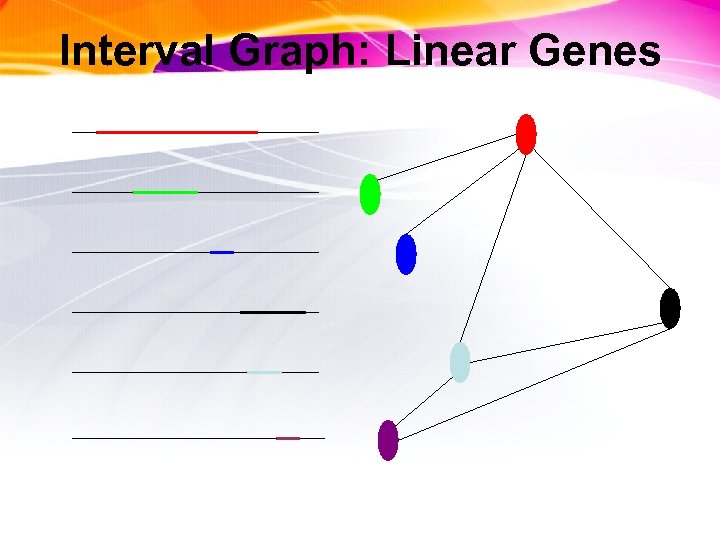Interval Graph: Linear Genes

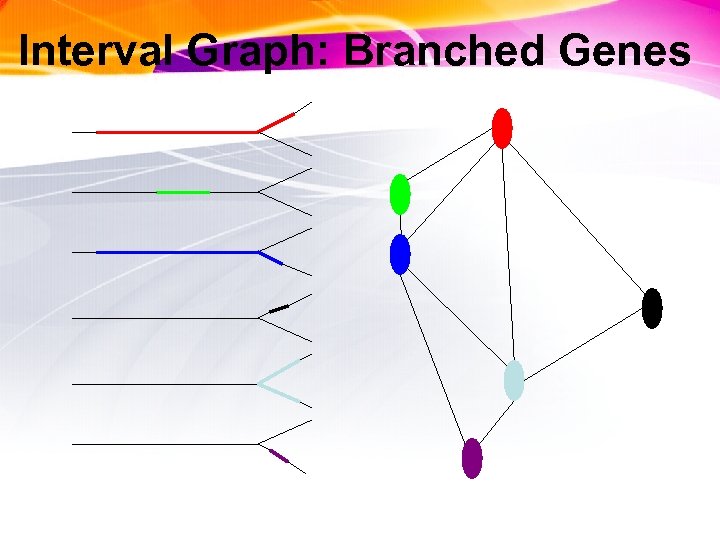Interval Graph: Branched Genes

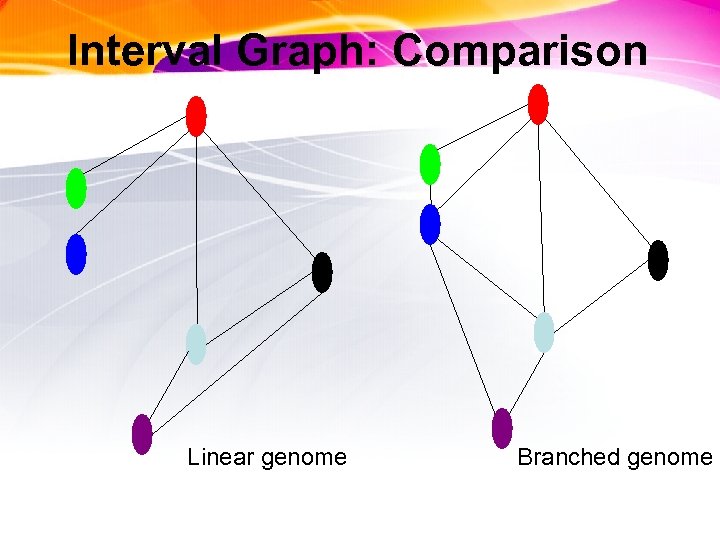Interval Graph: Comparison Linear genome Branched genome

3: DNA Sequencing: History Sanger method (1977): labeled dd. NTPs terminate DNA copying at random points. Gilbert method (1977): chemical method to cleave DNA at specific points (G, G+A, T+C, C). Both methods generate labeled fragments of varying lengths that are further electrophoresed.

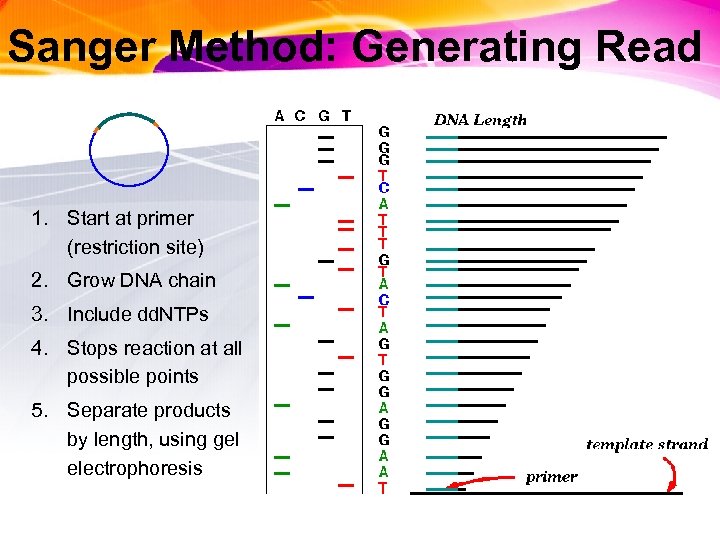Sanger Method: Generating Read 1. Start at primer (restriction site) 2. Grow DNA chain 3. Include dd. NTPs 4. Stops reaction at all possible points 5. Separate products by length, using gel electrophoresis

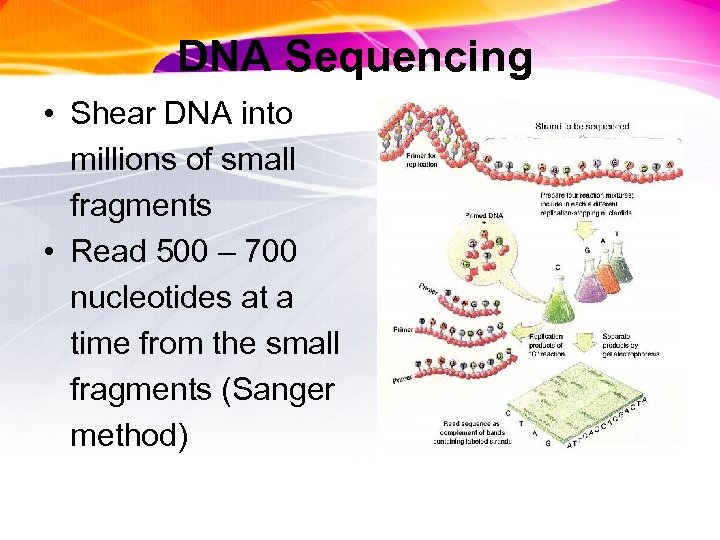DNA Sequencing • Shear DNA into millions of small fragments • Read 500 – 700 nucleotides at a time from the small fragments (Sanger method)

Fragment Assembly • Computational Challenge: assemble individual short fragments (reads) into a single genomic sequence (“superstring”) • Until late 1990 s the shotgun fragment assembly of human genome was viewed as intractable problem

4: Shortest Superstring Problem • Problem: Given a set of strings, find a shortest string that contains all of them • Input: Strings s 1, s 2, …. , sn • Output: A string s that contains all strings s 1, s 2, …. , sn as substrings, such that the length of s is minimized • Note: this formulation does not take into account sequencing errors

Shortest Superstring Problem: Example • Concatenating all eight strings results in a 24 letter superstring • the shortest superstring contains only 10 letters.

Conclusion and Qustions • Graphs graphs, vertex(vertices), edges, connected, disconnected, cycles, trees, degree, leaf • Graphs and Genetics • DNA Sequencing • Shortest Superstring Problem

References 1. http: //bix. ucsd. edu/bioalgorithms/slides. php 2. http: //en. wikipedia. org/wiki/Graph_theory 3. http: //simple. wikipedia. org/wiki/Genetics 4. http: //seqcore. brcf. med. umich. edu/doc/educ/dna pr/sequencing. html 5. http: //www. wiley. com/college/pratt/0471393878/s tudent/animations/dna_sequencing/index. html 6. http: //math. mit. edu/~goemans/18434 S 06/superst ring-lele. pdf