CHAPTER 8 COST BENEFIT ANALYSIS WHAT IS

CHAPTER 8: COST BENEFIT ANALYSIS

WHAT IS COST-BENEFIT ANALYSIS? Cost benefit analysis At first glance, cost benefit analysis seems like an accounting exercise of summing costs and benefits and determining if the ____________________suggesting that the benefits outweigh the costs However, cost-benefit analyses are rich in economic exercises —requiring a great deal of microeconomic application to accurately determine costs and benefits Accounting for the time frame in which costs and benefits accrue Determining opportunity costs of resources (more difficult in imperfectly competitive markets) Determining valuations of intangibles such as time saved, lives saved, reduction in noise, increased visibility, etc.

AN EXAMPLE—SEATTLE MONORAIL A few years ago Seattle voters decided whether or not to create a 14 mile long monorail system. The referendum included a 1. 4% excise tax on vehicles at a median cost of $100 per vehicle per year. How would the government decide if the project is worth undertaking? Consulting Firm hired to estimate costs and benefits: Expenditures included ($1. 68 billion) Costs of construction (labor and materials) Equipment purchases Buying permission from some property owners Visual impact (negative—some city views) Creation of noise (mostly offset by reduced noise from fewer buses once operational) Traffic delays during construction Benefits included: ($2. 07 billion) Commuters save $6. 4 million hours of travel time per year Reduction in parking fees for commuters ($4. 7 million) Reduction of car maintenance and operating costs 10 years Reduction of car and bus accidents

MEASURING CURRENT AND FUTURE COSTS AND BENEFITS 1. Project present dollars into the future and 2. Discount future dollars into the present Projecting Present dollars into the future:

NUMERICAL EXAMPLE $1000 today in the bank will grow at the rate of interest, say 1%, for a period of time of 2 years. R= $1000 r= 5% or. 01 t= 2 years

DISCOUNTING FUTURE DOLLARS INTO THE PRESENT R 0 = $1000 R 2 = $1000*(1+. 01)2 = $1020. 10 RT = R 0*(1+r)T o Rearrange to determine the present value: Present Value:

NUMERICAL EXAMPLE: DISCOUNTING FUTURE VALUES Suppose someone promises to pay you $100 at the end of two years. Assume the current rate of interest is 5%. What is the maximum amount you would give them today with the promise to repay $100 at the end of two years? o Need the “present discounted value” or PDV of the principal note if there is only one principal payout (R) as is the case here (and not different amounts year to year) then PDV= R/(1+r)t given by our previous formula For two years then: $100 in two years is equivalent to taking $90. 70 now and investing it at the current interest rate of 5%.

SPECIAL NOTES TO DISCOUNTING For many projects the costs or benefits (our R) will be different year to year. If this is the case you must discount each year separately and sum them.

DETERMINATION OF INTEREST RATE OR DISCOUNT RATE o For example, the next best project under consideration would yield a 10% return but with taxes owed on profits they will net 6% return. This 6% is used as “r”. for the government: In practice, the government uses a variety of discount rates. For both private sector and public sector, a sensitivity analysis is normally done showing outcomes at different “r” for evaluation (we will show an example shortly)

PRIVATE SECTOR: INTERNAL RATE OF RETURN (IROR) in essence, it finds the maximum interest rate or discount rate that makes the project financially viable. Example: if you have project X which requires $100 expenditure today and yields $110 a year from now then the IROR of the project would be: Calculating IROR for Project X: o Any rate lower than 10% makes the project more worthwhile because you are gaining $110 in two years with a $100 investment; at any rate of interest lower than 10% keeping the money in the bank would result in a worse outcome—something less than $110) Any rate higher than 10% makes keeping the money in the bank more attractive because it would yield more than $110 in two years.

PROBLEMS WITH IROR o Problem with IROR: if projects differ in size (dollar value) then IROR may not give as good as answer as PDV. IROR Project X: IROR Project Y: Looks like Project X might be preferred but since the size of the projects are different this isn’t necessarily the case:

IROR DOESN’T CONSIDER INTEREST COSTS Suppose the firm can borrow any amount of money at 6%. Now, Project Y looks better! Show instead evaluate the net returns (benefits-costs) across the life of the project and determine the present value of the net returns.

THE BEST METHOD OF DETERMINING A PROJECT’S REAL VALUE IS TO USE THE PRESENT DISCOUNTED VALUE PDV) OF THE PROJECT’S “NET ( RETURNS” Since many policies and programs have costs and benefits that accrue over time you must get the present value of benefits and the present value of costs to determine the PDV of the net return.

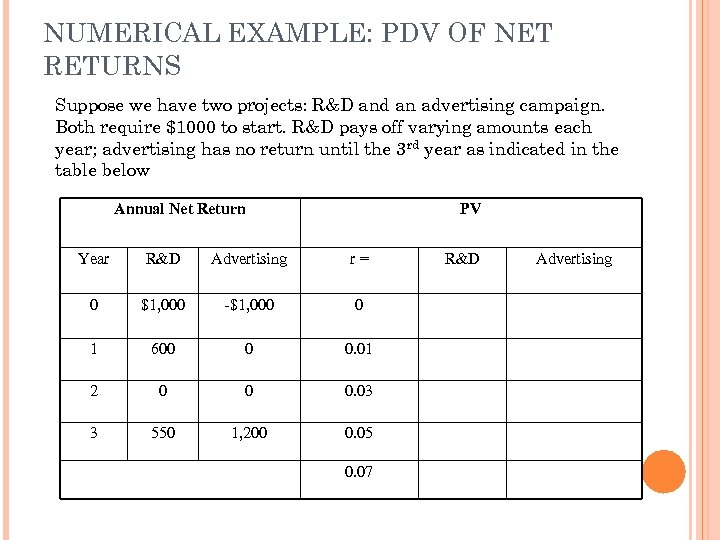
NUMERICAL EXAMPLE: PDV OF NET RETURNS Suppose we have two projects: R&D and an advertising campaign. Both require $1000 to start. R&D pays off varying amounts each year; advertising has no return until the 3 rd year as indicated in the table below Annual Net Return PV Year R&D Advertising r= 0 $1, 000 -$1, 000 0 1 600 0 0. 01 2 0 0 0. 03 3 550 1, 200 0. 05 0. 07 R&D Advertising

FILL IN PREVIOUS TABLE At r=0 for R&D: Fill At r=0. 07 for R&D in the rest of the table on your own:

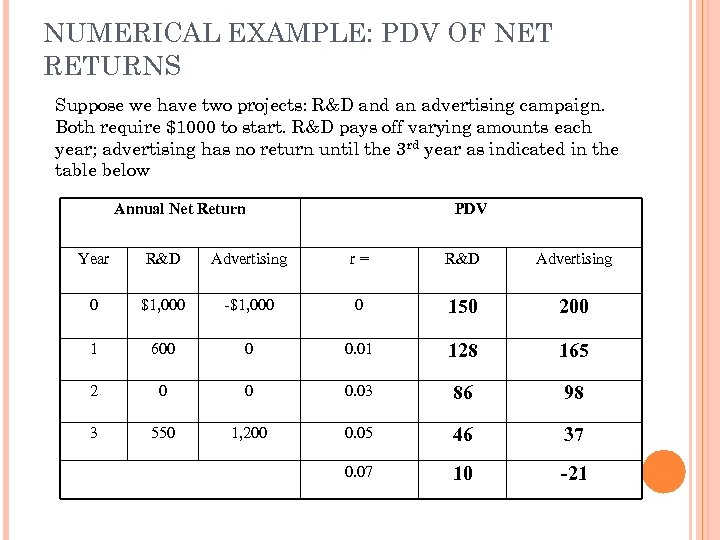
NUMERICAL EXAMPLE: PDV OF NET RETURNS Suppose we have two projects: R&D and an advertising campaign. Both require $1000 to start. R&D pays off varying amounts each year; advertising has no return until the 3 rd year as indicated in the table below Annual Net Return PDV Year R&D Advertising r= R&D Advertising 0 $1, 000 -$1, 000 0 150 200 1 600 0 0. 01 128 165 2 0 0 0. 03 86 98 3 550 1, 200 0. 05 46 37 0. 07 10 -21

TABLE OBSERVATIONS: What you observe is: However, at higher “r”: Why is this? At a lower discount rate the advertising benefits that accrue in the future and not heavily discounted when putting in present terms. At a higher discount rate, the advertising benefits that accrue in the future are heavily discounted and not worth as much in the present. This choice of a discount rate is critical for cost-benefit analysis!

MEASURING COSTS AND BENEFITS OF A PROJECT Example: Cost benefit Analysis of a Highway Construction Project—upgrading turnpike with crumbling roads Improvements require costs of: 1 million bags of asphalt 1 million hours of labor $10 million/year of maintenance costs Benefits: 500, 000 hrs of driving time saved/year Lives saved: 5/year

MEASURING COSTS OF THE PROJECT If a good such as asphalt is sold in a competitive market: ____________________________________________ If the labor market is competitive : __________________ So our costs are: $100 million for asphalt and $15 million for wages. Our maintenance cost involves both labor and materials and occurs over time. Must use present discounted value of the maintenance costs. o PDV= R 0 + R 1/(1 + r) + R 2/(1 + r)2 + Rn/(1 + r)n where r is the social discount rate. ; __________________________ For our example with maintenance costs of $10 million per year in perpetuity it would be valued at: _________________ Total costs are: ____________________________

WHAT IF AN INPUT (LABOR, MATERIALS) IS NOT SUPPLIED IN A PERFECTLY COMPETITIVE MARKET? With imperfect markets the price set by firms exceeds marginal cost P > MC For efficiency: Ex: monopolies or governments set a price floor (minimum wage) for a particular classification of workers such as construction workers. To determine the opportunity cost: _____________________________________________ Any money paid above and beyond that is considered simply a transfer of “rent” or “surplus” from the government (or provider) to the owner of the resource (workers). It is not included in the cost of the project.

MEASURING BENEFITS OF OUR PROJECT 1. 2. Value of driving time saved Value of lives saved Value of driving time saved A. Estimate the impact on society from reduced transportation costs of goods/services. B. Estimate the impact on individuals with reduced travel time to work or increase in leisure due to less time in traffic.

PART A: VALUE OF REDUCED TRANSPORTATION COSTS For producers, reduced in travel time means lower transportation cost of materials or final goods and services. A reduction in firm’s cost will increase supply This results in greater quantities of goods/services being purchased and sold in the market and lower prices. We must estimate the impact on total surplus—all economic agents—from this reduced cost.

GRAPH SHOWING CS, PS, TS BEFORE AND AFTER REDUCED TRANSPORTATION COSTS

PART B: ESTIMATE BENEFITS TO INDIVIDUALS FROM REDUCED DRIVING TIME—VALUING TIME The benefit of time saved is the value of each hour Does this valuation provide an accurate estimate? It can overstate the value: If you are employed for 40 hours and cannot be paid for extra hours then this wage of $17. 80 overstates the value of time saved. Your value of leisure may be below your wage rate. It can understate the value: What if your work environment is better than home (ex: air conditioning at work and not at home). Then the value of your wage understates benefits since your true benefit of arriving at work early is higher than your wage.

OTHER METHODS OF VALUING TIME Some studies have tried to determine the actual opportunity cost of time by looking at the difference between travel expense and time saved via different modes of transportation. Ex: Compare bus to train. Suppose riding the bus is less expensive but takes longer to arrive at work and the train is more expensive but results in less travel time. Estimate how much more people are willing to pay for the train to save time. This gives an estimate of how much they are willing to pay to reduce travel time or in essence what is the minimum value they place on their time.

OTHER TOOLS FOR MEASURING SUCH NON-MARKET BENEFITS 1. _________________: typically a survey approach in which people’s values are elicited. For example: respondents are asked to value their time or determine the value they place on certain goods. How much would you be willing to pay for x? or to avoid x? 2. ________________ compare people’s actual choices in markets and infer the value they place on certain attributes “people may lie but their actions which result from utility maximization do not!”

CONTINGENT VALUATION-PROBLEMS A. ______________—does the survey ask for one single valuation or does the survey elicit values for several different items when asked to value one item such as more visibility at Grand Canyon respondents provide 5 x the value than if asked this same question as the 3 rd question within a group of questions. B. ______________: the ordering of questions changes peoples’ valuations Example: two comparable surveys asked the value of saving a whale first and then the value of saving a seal. A second survey simply reversed the order. When valuation for seals was asked first they were worth $142 and whales $195. When reversed whales $172 and seals $85.

CV PROBLEMS CONTINUED C. ____________—respondents don’t necessarily value the actual, specific item, but the general type of good in answering questions If multiple surveys ask about valuation of wilderness areas (state parks), or preserving wildlife, etc. they all receive about same valuation despite specifics. It appears as though people value “wilderness” or “nature” by some amount regardless of the specific item we are trying to value

REVEALED PREFERENCE VALUATION Compare two identical houses with say a 5 minute difference in commute time. Differences in house prices may reveal difference in benefits. However, other attributes may differ also making this practically impossible. Note: Special regression analysis called “hedonic market analysis” is used to determine house values based on many factors including square footage, # bedrooms, # bathrooms, distance to town, etc. Still there are some unobservable characteristics or those hard to quantify like quality of the neighborhood.

THE VALUE OF A LIFE Many people suggest you cannot value a life in monetary terms or if such a value exists it should be infinite. This means that any project which saves 1 life would always be justified in a cost benefit analysis. Let’s look at two real world examples!

GM CARS AND VALUE OF A LIFE 1993: GM was publicly pressured to recall 5 million pickups from 1973 -1987 model years. Gas tanks were mounted on wrong side of the vehicle and activist groups claimed this made them more likely to explode on impact causing 150 deaths over this period the truck was manufactured. The recall would cost $1 billion and according to government calculations would save 32 more lives. Recall cost per life saved would be $1 billion/32=$31. 25 million! What happened? GM settled with the consumer group agreeing to provide $50 million to support educational programs about seat belts, drunk driving, etc, to invest in burn units and buy 200, 000 safety seats for low income families instead of recalling and fixing vehicles. Ralph Nader called this the “most unprecedented buyout of law enforcement officials by a culpable corporation in regulatory history”. Was it? Government estimated that child safety seats alone would save 50 lives for $50 million price tag—less than $1 million per life.

LONDON COMMUTER TRAIN CRASH 1999, commuter train crash in London occurred shortly after the rail was privatized. Private citizens believed the profit-driven firm had skimped on safety features and demanded the government require an upgraded system. Initially, government responded by saying they would provide additional safety “at any cost. ” The first system investigated to stop trains in emergency at under 75 mph would cost $700 million. The committee then found a second system that would stop any train at any speed costing between $3 and $9 billion. This system would save 1 -3 lives per year and last 30 -50 years. This equates to approximately $300 million per life saved. Critics got the government to back down from promises to increase rail safety by showing increasing road safety saves lives at only a cost of $2 million per life!

TOOLS FOR VALUING LIFE 1. 2. 3.

LIFETIME WAGES Value a life based upon lifetime stream of wages—how much income a person would generate in their lifetime Nor does it include utility derived from friends and family from the person being alive. Implication: economists discount this method because of its shortcomings and implications.

CONTINGENT VALUATION Contingent valuation—in effect you attempt to determine how much one value’s life by asking about the value placed on items that change the probability of dying how much less would you pay for a house near environmental problem that may reduce your life by 1 year vs. identical house without these issues? In effect, the price differential tells us how much you value 1 year of your life. Again, obvious problems with contingent valuation with hypothetical questions, people understanding the true impact of 1 year life loss, etc.

REVEALED PREFERENCE AND VALUING LIFE Revealed preference: look at choices people made that increase probability of living longer or reducing the probability of death. The choice to purchase an optional passenger side air bag in your car. If cost is $350 and installation has 1 in 10, 000 chance at saving a life then implied the value of life is $3. 5 million. Strong assumptions— Studies of this nature end up with implied values of life between _________________ This seems as if it may not provide “good” information but it provides enough information to rule out projects that value an average life say at $100 million.

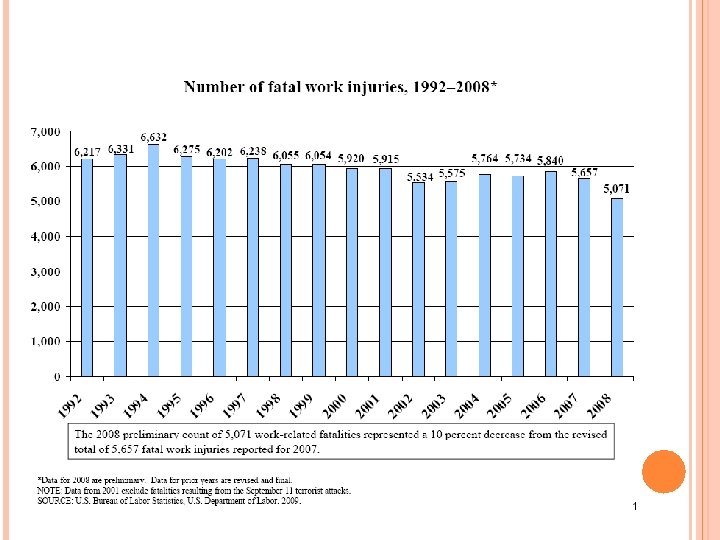
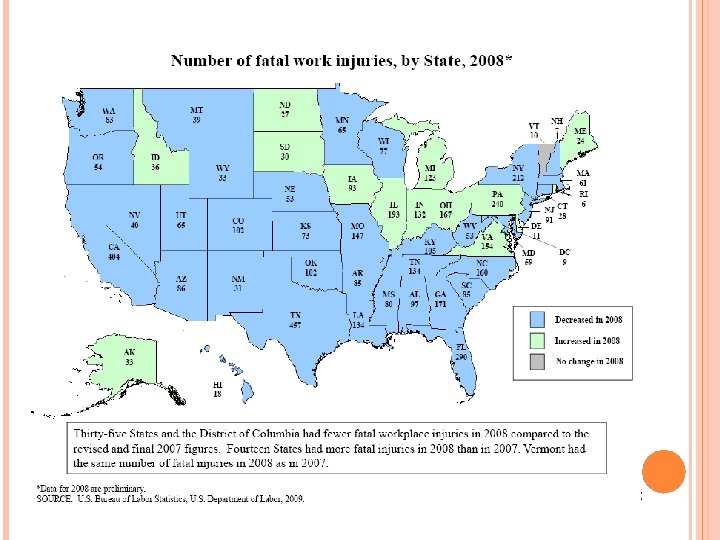
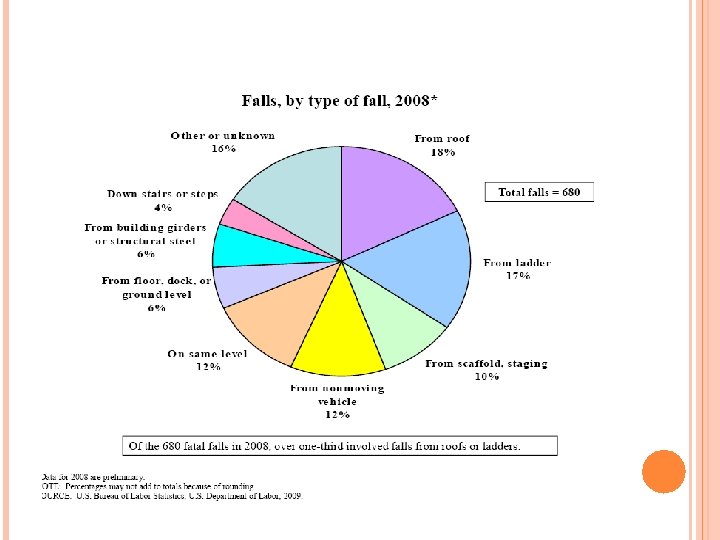
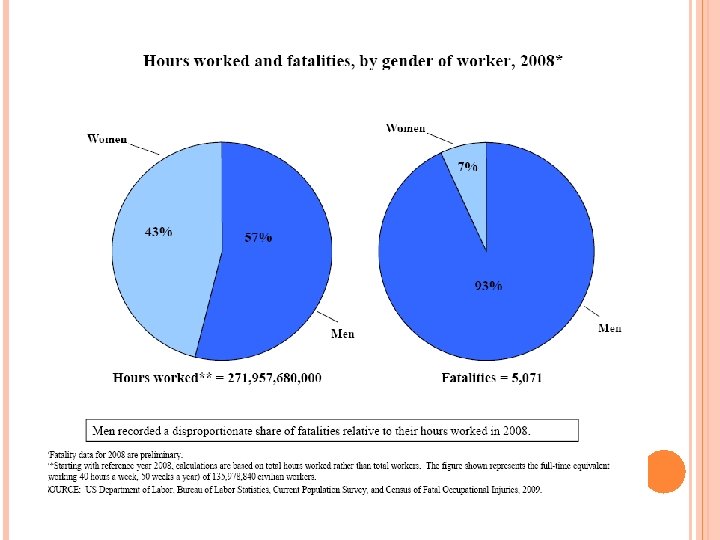
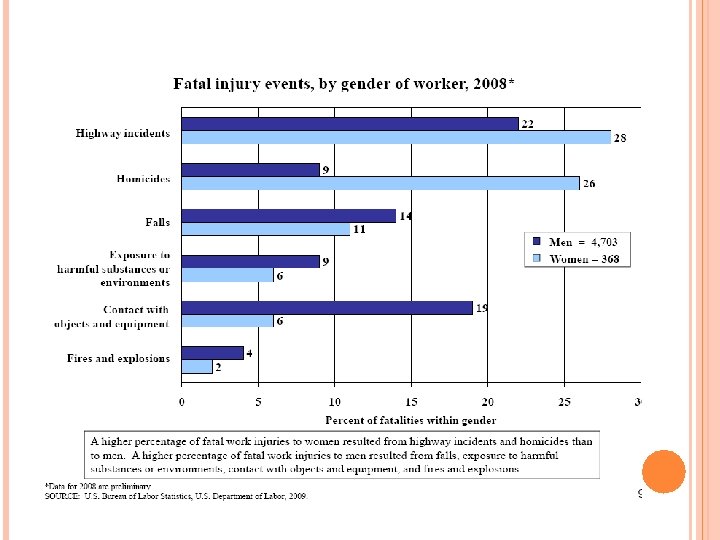
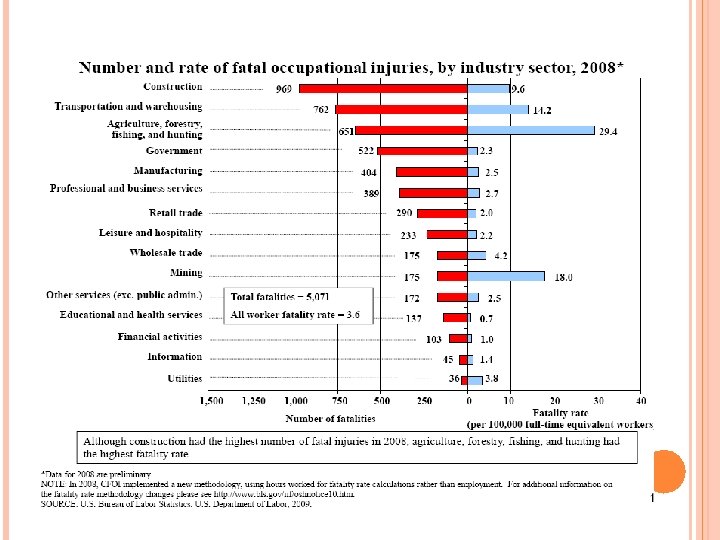
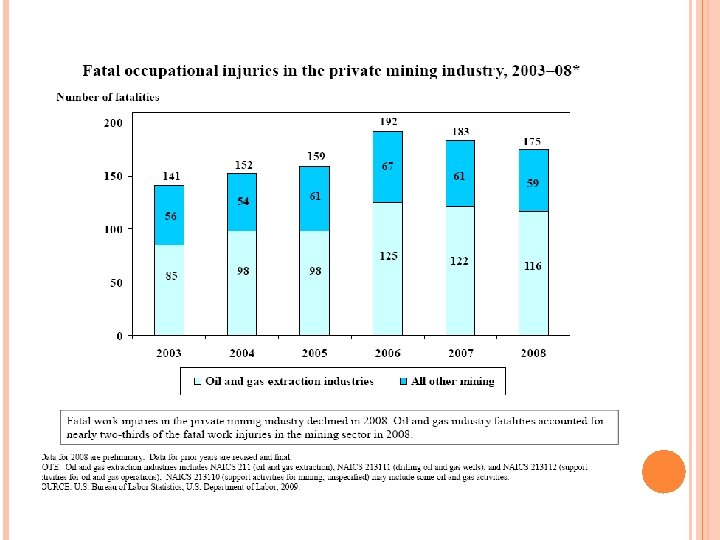
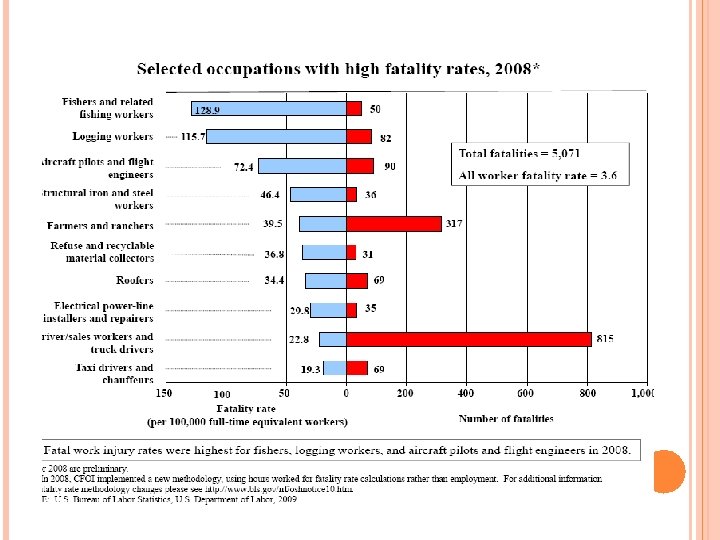
REVEALED PREFERENCE CONTINUED Choice of occupation and relationship between occupational risk (fatality rates or injury rates) and wages. Or how much individuals need to be paid to be employed in a risky job (such as one with 1% higher death rate). Strong assumptions—must know these probabilities to make informed decisions. Bureau of Labor Statistics (BLS. GOV) data