Chapter 8 Clustering 1 Searching for groups

Chapter 8: Clustering 1

Searching for groups n n n Clustering is unsupervised or undirected. Unlike classification, in clustering, no preclassified data. Search for groups or clusters of data points (records) that are similar to one another. n Similar points may mean: similar customers, products, that will behave in similar ways. 2

Group similar points together n Group points into classes using some distance measures. n n Within-cluster distance, and between cluster distance Applications: n n As a stand-alone tool to get insight into data distribution As a preprocessing step for other algorithms 3

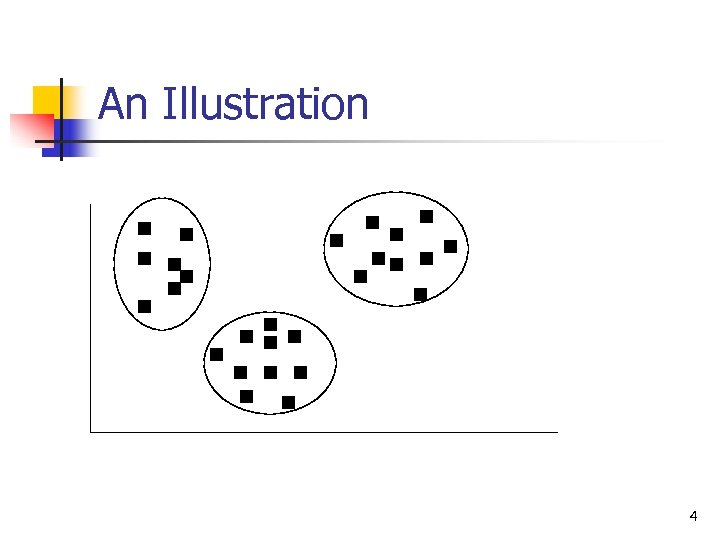An Illustration 4

Examples of Clustering Applications n n n Marketing: Help marketers discover distinct groups in their customer bases, and then use this knowledge to develop targeted marketing programs Insurance: Identifying groups of motor insurance policy holders with some interesting characteristics. City-planning: Identifying groups of houses according to their house type, value, and geographical location 5

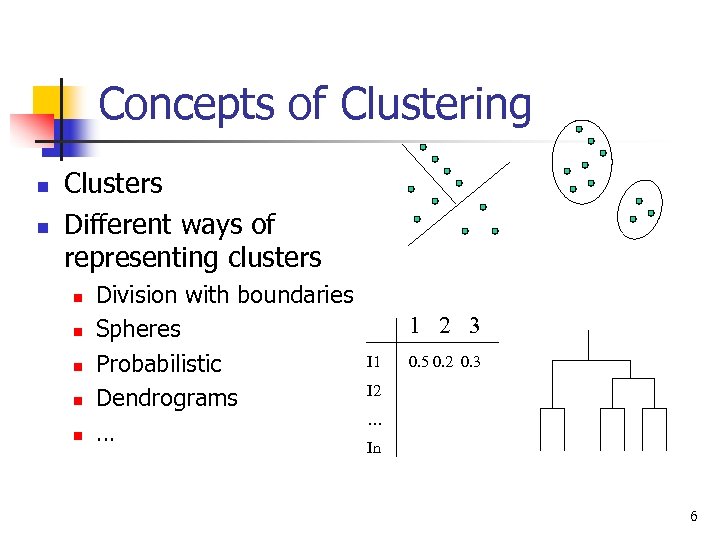Concepts of Clustering n n Clusters Different ways of representing clusters n n n Division with boundaries Spheres Probabilistic Dendrograms … 1 2 3 I 1 0. 5 0. 2 0. 3 I 2 … In 6

Clustering n Clustering quality n n n Inter-clusters distance maximized Intra-clusters distance minimized The quality of a clustering result depends on both the similarity measure used by the method and its application. The quality of a clustering method is also measured by its ability to discover some or all of the hidden patterns Clustering vs. classification n n Which one is more difficult? Why? There a huge number of clustering techniques. 7

Dissimilarity/Distance Measure n n Dissimilarity/Similarity metric: Similarity is expressed in terms of a distance function, which is typically metric: d (i, j) The definitions of distance functions are usually very different for interval-scaled, boolean, categorical, ordinal and ratio variables. Weights should be associated with different variables based on applications and data semantics. It is hard to define “similar enough” or “good enough”. The answer is typically highly subjective. 8

Types of data in clustering analysis n Interval-scaled variables n Binary variables n Nominal, ordinal, and ratio variables n Variables of mixed types 9

Interval-valued variables n n Continuous measurements in a roughly linear scale, e. g. , weight, height, temperature, etc Standardize data (depending on applications) n Calculate the mean absolute deviation: where n Calculate the standardized measurement (z-score) 10

Similarity Between Objects n n Distance: Measure the similarity or dissimilarity between two data objects Some popular ones include: Minkowski distance: where (xi 1, xi 2, …, xip) and (xj 1, xj 2, …, xjp) are two pdimensional data objects, and q is a positive integer n If q = 1, d is Manhattan distance 11

Similarity Between Objects (Cont. ) n If q = 2, d is Euclidean distance: n Properties n n n d(i, j) 0 d(i, i) = 0 d(i, j) = d(j, i) d(i, j) d(i, k) + d(k, j) Also, one can use weighted distance, and many other similarity/distance measures. 12

Binary Variables n A contingency table for binary data Object j Object i n Simple matching coefficient (invariant, if the binary variable is symmetric): n Jaccard coefficient (noninvariant if the binary variable is asymmetric): 13

Dissimilarity of Binary Variables n Example n n n gender is a symmetric attribute (not used below) the remaining attributes are asymmetric attributes let the values Y and P be set to 1, and the value N be set to 0 14

Nominal Variables n n A generalization of the binary variable in that it can take more than 2 states, e. g. , red, yellow, blue, green, etc Method 1: Simple matching n n m: # of matches, p: total # of variables Method 2: use a large number of binary variables n creating a new binary variable for each of the M nominal states 15

Ordinal Variables n An ordinal variable can be discrete or continuous n Order is important, e. g. , rank n Can be treated like interval-scaled (f is a variable) n n n replace xif by their ranks map the range of each variable onto [0, 1] by replacing i-th object in the f-th variable by compute the dissimilarity using methods for intervalscaled variables 16

Ratio-Scaled Variables n n Ratio-scaled variable: a measurement on a nonlinear scale, approximately at exponential scale, such as Ae. Bt or Ae-Bt, e. g. , growth of a bacteria population. Methods: n n treat them like interval-scaled variables—not a good idea! (why? —the scale can be distorted) apply logarithmic transformation yif = log(xif) n treat them as continuous ordinal data and then treat their ranks as interval-scaled 17

Variables of Mixed Types n A database may contain all six types of variables n n symmetric binary, asymmetric binary, nominal, ordinal, interval and ratio One may use a weighted formula to combine their effects n n n f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 o. w. f is interval-based: use the normalized distance f is ordinal or ratio-scaled n compute ranks rif and n and treat zif as interval-scaled 18

Major Clustering Techniques n n Partitioning algorithms: Construct various partitions and then evaluate them by some criterion Hierarchy algorithms: Create a hierarchical decomposition of the set of data (or objects) using some criterion Density-based: based on connectivity and density functions Model-based: A model is hypothesized for each of the clusters and the idea is to find the best fit of the model to each other. 19

Partitioning Algorithms: Basic Concept n n Partitioning method: Construct a partition of a database D of n objects into a set of k clusters Given a k, find a partition of k clusters that optimizes the chosen partitioning criterion n Global optimal: exhaustively enumerate all partitions n Heuristic methods: k-means and k-medoids algorithms n n k-means : Each cluster is represented by the center of the cluster k-medoids or PAM (Partition around medoids): Each cluster is represented by one of the objects in the cluster 20

The K-Means Clustering n Given k, the k-means algorithm is as follows: 1) Choose k cluster centers to coincide with k randomly-chosen points 2) Assign each data point to the closest cluster center 3) Recompute the cluster centers using the current cluster memberships. 4) If a convergence criterion is not met, go to 2). Typical convergence criteria are: no (or minimal) reassignment of data points to new cluster centers, or minimal decrease in squared error. p is a point and mi is the mean of cluster Ci 21

Example n For simplicity, 1 dimensional data and k=2. data: 1, 2, 5, 6, 7 n K-means: n n n Randomly select 5 and 6 as initial centroids; => Two clusters {1, 2, 5} and {6, 7}; mean. C 1=8/3, mean. C 2=6. 5 => {1, 2}, {5, 6, 7}; mean. C 1=1. 5, mean. C 2=6 => no change. Aggregate dissimilarity = 0. 5^2 + 1^2 = 2. 5 22

Comments on K-Means n n n Strength: efficient: O(tkn), where n is # data points, k is # clusters, and t is # iterations. Normally, k, t << n. Comment: Often terminates at a local optimum. The global optimum may be found using techniques such as: deterministic annealing and genetic algorithms Weakness n n n Applicable only when mean is defined, difficult for categorical data Need to specify k, the number of clusters, in advance Sensitive to noisy data and outliers Not suitable to discover clusters with non-convex shapes Sensitive to initial seeds 23

Variations of the K-Means Method n A few variants of the k-means which differ in n n Dissimilarity measures n n Selection of the initial k seeds Strategies to calculate cluster means Handling categorical data: k-modes n n n Replacing means of clusters with modes Using new dissimilarity measures to deal with categorical objects Using a frequency based method to update modes of clusters 24

k-Medoids clustering method n k-Means algorithm is sensitive to outliers n n n Since an object with an extremely large value may substantially distort the distribution of the data. Medoid – the most centrally located point in a cluster, as a representative point of the cluster. An example Initial Medoids n In contrast, a centroid is not necessarily inside a cluster. 25

Partition Around Medoids n PAM: 1. 2. 3. 4. Given k Randomly pick k instances as initial medoids Assign each data point to the nearest medoid x Calculate the objective function n 5. 6. 7. the sum of dissimilarities of all points to their nearest medoids. (squared-error criterion) Randomly select an point y Swap x by y if the swap reduces the objective function Repeat (3 -6) until no change 26

Comments on PAM n n Pam is more robust than k-means in the presence of noise and outliers because a medoid is less influenced by outliers or other extreme values than a mean (why? ) Outlier (100 unit away) Pam works well for small data sets but does not scale well for large data sets. n O(k(n-k)2 ) for each change where n is # of data, k is # of clusters 27

CLARA: Clustering Large Applications n n CLARA: Built in statistical analysis packages, such as S+ It draws multiple samples of the data set, applies PAM on each sample, and gives the best clustering as the output Strength: deals with larger data sets than PAM Weakness: n n n Efficiency depends on the sample size A good clustering based on samples will not necessarily represent a good clustering of the whole data set if the sample is biased There are other scale-up methods e. g. , CLARANS 28

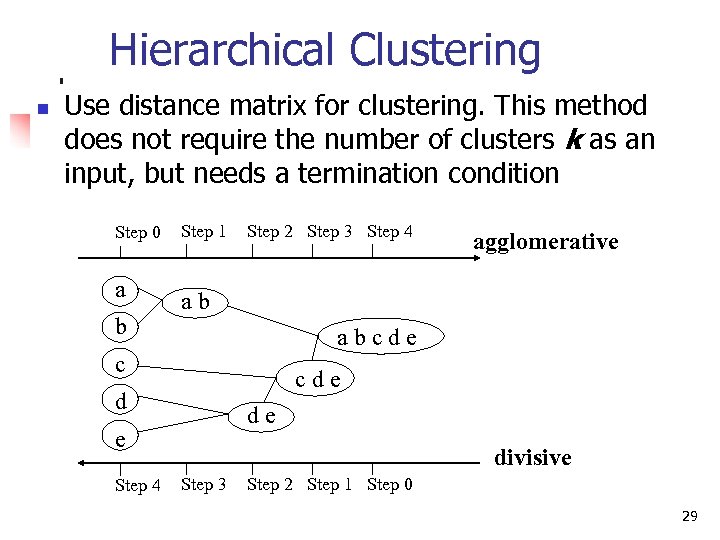Hierarchical Clustering n Use distance matrix for clustering. This method does not require the number of clusters k as an input, but needs a termination condition Step 0 a b Step 1 Step 2 Step 3 Step 4 ab abcde c cde d de e Step 4 agglomerative divisive Step 3 Step 2 Step 1 Step 0 29

Agglomerative Clustering At the beginning, each data point forms a cluster (also called a node). Merge nodes/clusters that have the least dissimilarity. Go on merging Eventually all nodes belong to the same cluster 30

A Dendrogram Shows How the Clusters are Merged Hierarchically Decompose data objects into a several levels of nested partitioning (tree of clusters), called a dendrogram. A clustering of the data objects is obtained by cutting the dendrogram at the desired level, then each connected component forms a cluster. 31

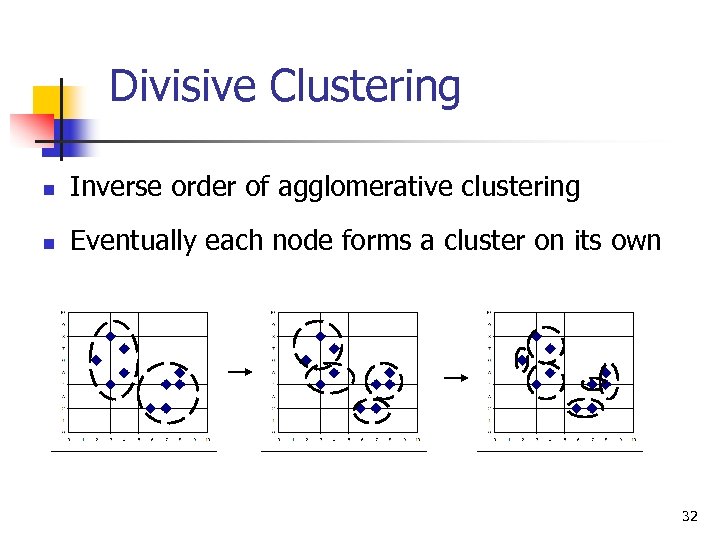Divisive Clustering n Inverse order of agglomerative clustering n Eventually each node forms a cluster on its own 32

More on Hierarchical Methods n Major weakness of agglomerative clustering methods n n n do not scale well: time complexity at least O(n 2), where n is the total number of objects can never undo what was done previously Integration of hierarchical with distance-based clustering to scale-up these clustering methods n n BIRCH (1996): uses CF-tree and incrementally adjusts the quality of sub-clusters CURE (1998): selects well-scattered points from the cluster and then shrinks them towards the center of the cluster by a specified fraction 33

Summary n n n Cluster analysis groups objects based on their similarity and has wide applications Measure of similarity can be computed for various types of data Clustering algorithms can be categorized into partitioning methods, hierarchical methods, density-based methods, etc Clustering can also be used for outlier detection which are useful for fraud detection What is the best clustering algorithm? 34