Chapter 7 Work and Energy 7 -2

Chapter 7 Work and Energy

7 -2 Scalar Product of Two Vectors Example 7 -4: Using the dot product. The force shown has magnitude FP = 20 N and makes an angle of 30° to the ground. Calculate the work done by this force, using the dot product, when the wagon is dragged 100 m along the ground.

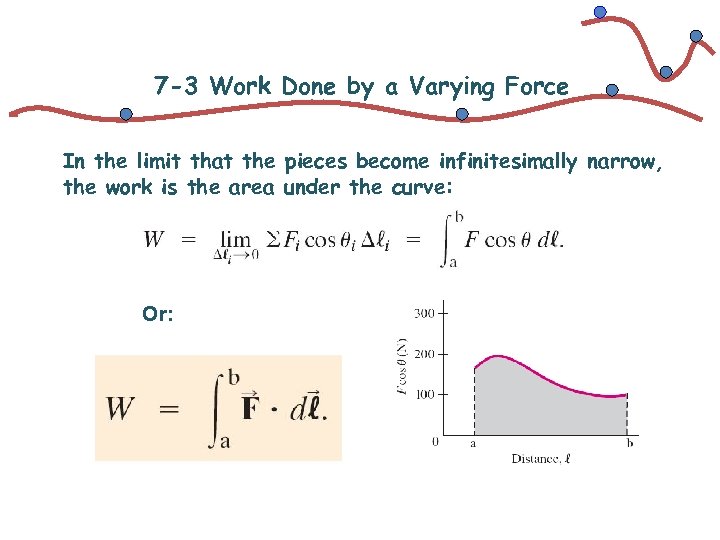7 -3 Work Done by a Varying Force In the limit that the pieces become infinitesimally narrow, the work is the area under the curve: Or:

7 -3 Work Done by a Varying Force Work done by a spring force: This is called Hooke’s law

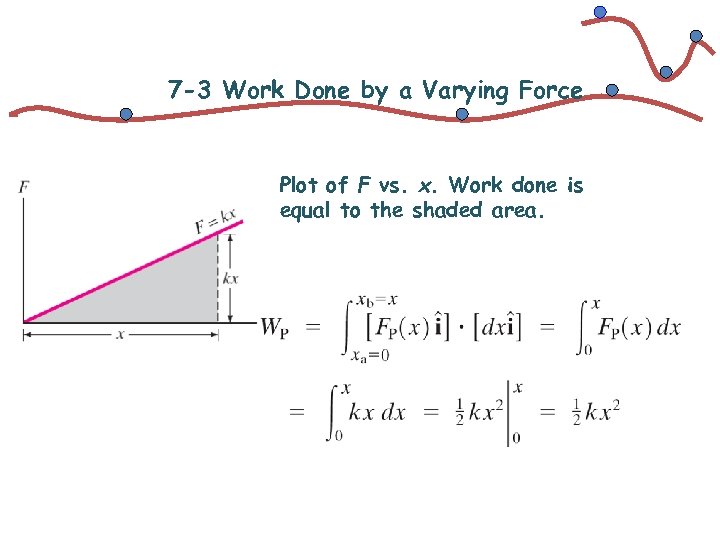7 -3 Work Done by a Varying Force Plot of F vs. x. Work done is equal to the shaded area.

7 -3 Work Done by a Varying Force Example 7 -5: Work done on a spring. (a) A person pulls on a spring, stretching it 3. 0 cm, which requires a maximum force of 75 N. How much work does the person do? (b) If, instead, the person compresses the spring 3. 0 cm, how much work does the person do?

7 -3 Work Done by a Varying Force Example 7 -6: Force as a function of x. A robot arm that controls the position of a video camera in an automated surveillance system is manipulated by a motor that exerts a force on the arm. The force is given by where F 0 = 2. 0 N, x 0 = 0. 0070 m, and x is the position of the end of the arm. If the arm moves from x 1 = 0. 010 m to x 2 = 0. 050 m, how much work did the motor do?

Problem 35 • (II) A spring has a constant k=65 N/m. Draw a graph of the spring force F versus the stretch distance, and use it to determine the work needed to stretch the spring from x= 3 cm to x= 6. 5 cm where x=0 cm refers to the spring’s unstretched length.

Problem 43 (II) The force needed to hold a particular spring compressed an amount x from its normal length is given by kx+ax 3+bx 4. How much work must be done to compress it by an amount X, starting from X = 0.

7 -4 Kinetic Energy and the Work-Energy Principle Energy was traditionally defined as the ability to do work. All forces are able to do work; however, we are dealing in these chapters with mechanical energy, which does follow this definition.

7 -4 Kinetic Energy and the Work-Energy Principle If we write the acceleration in terms of the velocity and the distance, we find that the work done here is We define the kinetic energy as:

7 -4 Kinetic Energy and the Work-Energy Principle This means that the work done is equal to the change in the kinetic energy: This is the Work-Energy Principle: • If the net work is positive, the kinetic energy increases. • If the net work is negative, the kinetic energy decreases.

7 -4 Kinetic Energy and the Work-Energy Principle Because work and kinetic energy can be equated, they must have the same units: kinetic energy is measured in joules. Energy can be considered as the ability to do work:

7 -4 Kinetic Energy and the Work-Energy Principle Example 7 -7: Kinetic energy and work done on a baseball. A 145 -g baseball is thrown so that it acquires a speed of 25 m/s. (a) What is its kinetic energy? (b) What was the net work done on the ball to make it reach this speed, if it started from rest?

7 -4 Kinetic Energy and the Work-Energy Principle Example 7 -8: Work on a car, to increase its kinetic energy. How much net work is required to accelerate a 1000 -kg car from 20 m/s to 30 m/s? The net work is positive so there is an increase in kinetic energy

7 -4 Kinetic Energy and the Work-Energy Principle Example 7 -10: A compressed spring. A horizontal spring has spring constant k = 360 N/m. (a) How much work is required to compress it from its uncompressed length (x = 0) to x = 11. 0 cm? (b) If a 1. 85 -kg block is placed against the spring and the spring is released, what will be the speed of the block when it separates from the spring at x = 0? Ignore friction. (c) Repeat part (b) but assume that the block is moving on a table and that some kind of constant drag force FD = 7. 0 N is acting to slow it down, such as friction (or perhaps your finger).