f7b38784faea46dc8e523271081321e0.ppt
- Количество слайдов: 101

Chapter 7 Hypothesis Testing with One Sample Larson/Farber 4 th ed. 1

Chapter Outline • • • 7. 1 Introduction to Hypothesis Testing 7. 2 Hypothesis Testing for the Mean (Large Samples) 7. 3 Hypothesis Testing for the Mean (Small Samples) 7. 4 Hypothesis Testing for Proportions 7. 5 Hypothesis Testing for Variance and Standard Deviation Larson/Farber 4 th ed. 2

Section 7. 1 Introduction to Hypothesis Testing Larson/Farber 4 th ed. 3

Section 7. 1 Objectives • State a null hypothesis and an alternative hypothesis • Identify type I and type I errors and interpret the level of significance • Determine whether to use a one-tailed or two-tailed statistical test and find a p-value • Make and interpret a decision based on the results of a statistical test • Write a claim for a hypothesis test Larson/Farber 4 th ed. 4

Hypothesis Tests Hypothesis test • A process that uses sample statistics to test a claim about the value of a population parameter. • For example: An automobile manufacturer advertises that its new hybrid car has a mean mileage of 50 miles per gallon. To test this claim, a sample would be taken. If the sample mean differs enough from the advertised mean, you can decide the advertisement is wrong. Larson/Farber 4 th ed. 5

Hypothesis Tests Statistical hypothesis • A statement, or claim, about a population parameter. • Need a pair of hypotheses • one that represents the claim • the other, its complement • When one of these hypotheses is false, the other must be true. Larson/Farber 4 th ed. 6

Stating a Hypothesis Null hypothesis • A statistical hypothesis that contains a statement of equality such as , =, or . • Denoted H 0 read “H subzero” or “H naught. ” Alternative hypothesis • A statement of inequality such as >, , or <. • Must be true if H 0 is false. • Denoted Ha read “H sub -a. ” complementary statements Larson/Farber 4 th ed. 7

Stating a Hypothesis • To write the null and alternative hypotheses, translate the claim made about the population parameter from a verbal statement to a mathematical statement. • Then write its complement. H 0: μ ≤ k Ha : μ > k H 0: μ ≥ k Ha : μ < k H 0: μ = k Ha : μ ≠ k • Regardless of which pair of hypotheses you use, you always assume μ = k and examine the sampling distribution on the basis of this assumption. Larson/Farber 4 th ed. 8

Example: Stating the Null and Alternative Hypotheses Write the claim as a mathematical sentence. State the null and alternative hypotheses and identify which represents the claim. 1. A university publicizes that the proportion of its students who graduate in 4 years is 82%. Solution: H 0: p = 0. 82 Equality condition (Claim) Ha: p ≠ 0. 82 Complement of H 0 Larson/Farber 4 th ed. 9

Example: Stating the Null and Alternative Hypotheses Write the claim as a mathematical sentence. State the null and alternative hypotheses and identify which represents the claim. 2. A water faucet manufacturer announces that the mean flow rate of a certain type of faucet is less than 2. 5 gallons per minute. Solution: H 0: μ ≥ 2. 5 gallons per minute Ha: μ < 2. 5 gallons per minute Larson/Farber 4 th ed. Complement of Ha Inequality (Claim) condition 10

Example: Stating the Null and Alternative Hypotheses Write the claim as a mathematical sentence. State the null and alternative hypotheses and identify which represents the claim. 3. A cereal company advertises that the mean weight of the contents of its 20 -ounce size cereal boxes is more than 20 ounces. Solution: H 0: μ ≤ 20 ounces Ha: μ > 20 ounces Larson/Farber 4 th ed. Complement of Ha Inequality (Claim) condition 11

Types of Errors • No matter which hypothesis represents the claim, always begin the hypothesis test assuming that the equality condition in the null hypothesis is true. • At the end of the test, one of two decisions will be made: § reject the null hypothesis § fail to reject the null hypothesis • Because your decision is based on a sample, there is the possibility of making the wrong decision. Larson/Farber 4 th ed. 12

Types of Errors Decision Do not reject H 0 Reject H 0 Actual Truth of H 0 is true H 0 is false Correct Decision Type II Error Type I Error Correct Decision • A type I error occurs if the null hypothesis is rejected when it is true. • A type II error occurs if the null hypothesis is not rejected when it is false. Larson/Farber 4 th ed. 13

Example: Identifying Type I and Type II Errors The USDA limit for salmonella contamination for chicken is 20%. A meat inspector reports that the chicken produced by a company exceeds the USDA limit. You perform a hypothesis test to determine whether the meat inspector’s claim is true. When will a type I or type II error occur? Which is more serious? (Source: United States Department of Agriculture) Larson/Farber 4 th ed. 14

Solution: Identifying Type I and Type II Errors Let p represent the proportion of chicken that is contaminated. Hypotheses: H 0: p ≤ 0. 2 Ha: p > 0. 2 (Claim) Chicken meets USDA limits. H 0: p ≤ 0. 20 0. 16 Larson/Farber 4 th ed. 0. 18 Chicken exceeds USDA limits. H 0: p > 0. 20 0. 22 0. 24 p 15

Solution: Identifying Type I and Type II Errors Hypotheses: H 0: p ≤ 0. 2 Ha: p > 0. 2 (Claim) A type I error is rejecting H 0 when it is true. The actual proportion of contaminated chicken is less than or equal to 0. 2, but you decide to reject H 0. A type II error is failing to reject H 0 when it is false. The actual proportion of contaminated chicken is greater than 0. 2, but you do not reject H 0. Larson/Farber 4 th ed. 16

Solution: Identifying Type I and Type II Errors Hypotheses: H 0: p ≤ 0. 2 Ha: p > 0. 2 (Claim) • With a type I error, you might create a health scare and hurt the sales of chicken producers who were actually meeting the USDA limits. • With a type II error, you could be allowing chicken that exceeded the USDA contamination limit to be sold to consumers. • A type II error could result in sickness or even death. Larson/Farber 4 th ed. 17

Level of Significance Level of significance • Your maximum allowable probability of making a type I error. § Denoted by , the lowercase Greek letter alpha. • By setting the level of significance at a small value, you are saying that you want the probability of rejecting a true null hypothesis to be small. • Commonly used levels of significance: § = 0. 10 = 0. 05 = 0. 01 • P(type II error) = β (beta) Larson/Farber 4 th ed. 18

Statistical Tests • After stating the null and alternative hypotheses and specifying the level of significance, a random sample is taken from the population and sample statistics are calculated. • The statistic that is compared with the parameter in the null hypothesis is called the test statistic. Population parameter Test statistic μ p σ2 Larson/Farber 4 th ed. s 2 Standardized test statistic z (Section 7. 2 n 30) t (Section 7. 3 n < 30) z (Section 7. 4) χ2 (Section 7. 5) 19

P-values P-value (or probability value) • The probability, if the null hypothesis is true, of obtaining a sample statistic with a value as extreme or more extreme than the one determined from the sample data. • Depends on the nature of the test. Larson/Farber 4 th ed. 20

Nature of the Test • Three types of hypothesis tests § left-tailed test § right-tailed test § two-tailed test • The type of test depends on the region of the sampling distribution that favors a rejection of H 0. • This region is indicated by the alternative hypothesis. Larson/Farber 4 th ed. 21

Left-tailed Test • The alternative hypothesis Ha contains the less-than inequality symbol (<). H 0: μ k Ha : μ < k P is the area to the left of the test statistic. z -3 -2 -1 0 1 2 3 Test statistic Larson/Farber 4 th ed. 22
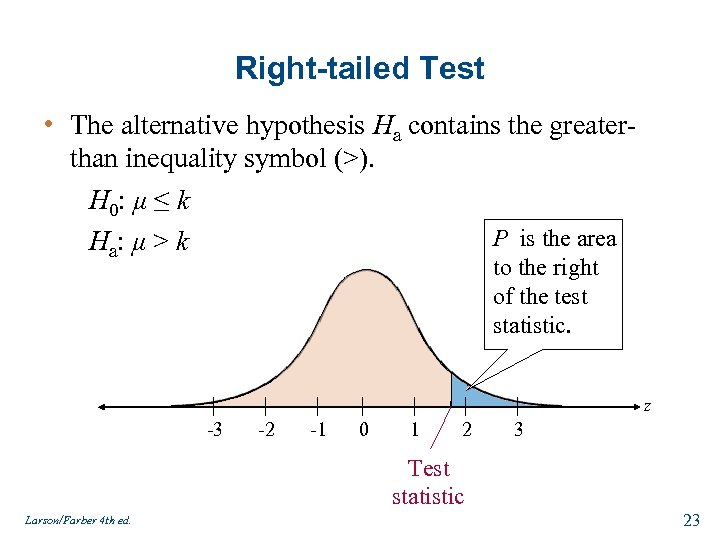
Right-tailed Test • The alternative hypothesis Ha contains the greaterthan inequality symbol (>). H 0: μ ≤ k P is the area Ha : μ > k to the right of the test statistic. z -3 -2 -1 0 1 2 3 Test statistic Larson/Farber 4 th ed. 23

Two-tailed Test • The alternative hypothesis Ha contains the not equal inequality symbol (≠). Each tail has an area of ½P. H 0: μ = k Ha : μ k P is twice the area to the right of the positive test statistic. P is twice the area to the left of the negative test statistic. z -3 Larson/Farber 4 th ed. -2 -1 Test statistic 0 1 2 Test statistic 3 24

Example: Identifying The Nature of a Test For each claim, state H 0 and Ha. Then determine whether the hypothesis test is a left-tailed, right-tailed, or two-tailed test. Sketch a normal sampling distribution and shade the area for the P-value. 1. A university publicizes that the proportion of its students who graduate in 4 years is 82%. Solution: H 0: p = 0. 82 ½ P-value Ha: p ≠ 0. 82 area Two-tailed test Larson/Farber 4 th ed. -z 0 z z 25
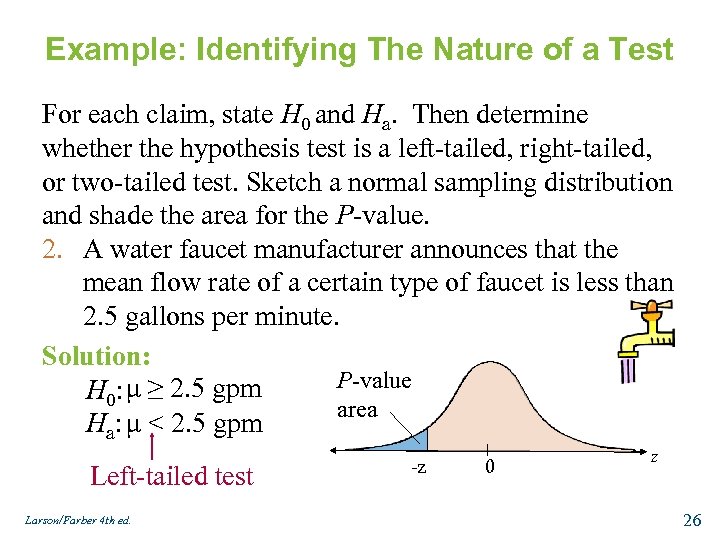
Example: Identifying The Nature of a Test For each claim, state H 0 and Ha. Then determine whether the hypothesis test is a left-tailed, right-tailed, or two-tailed test. Sketch a normal sampling distribution and shade the area for the P-value. 2. A water faucet manufacturer announces that the mean flow rate of a certain type of faucet is less than 2. 5 gallons per minute. Solution: P-value H 0: μ ≥ 2. 5 gpm area μ < 2. 5 gpm Ha : Left-tailed test Larson/Farber 4 th ed. -z 0 z 26

Example: Identifying The Nature of a Test For each claim, state H 0 and Ha. Then determine whether the hypothesis test is a left-tailed, right-tailed, or two-tailed test. Sketch a normal sampling distribution and shade the area for the P-value. 3. A cereal company advertises that the mean weight of the contents of its 20 -ounce size cereal boxes is more than 20 ounces. Solution: P-value H 0: μ ≤ 20 oz area Ha: μ > 20 oz Right-tailed test Larson/Farber 4 th ed. 0 z z 27

Making a Decision Rule Based on P-value • Compare the P-value with . § If P , then reject H 0. § If P > , then fail to reject H 0. Claim Decision Claim is H 0 Claim is Ha Reject H 0 There is enough evidence to reject the claim There is enough evidence to support the claim Fail to reject H 0 There is not enough evidence to reject the claim There is not enough evidence to support the claim Larson/Farber 4 th ed. 28

Example: Interpreting a Decision You perform a hypothesis test for the following claim. How should you interpret your decision if you reject H 0? If you fail to reject H 0? 1. H 0 (Claim): A university publicizes that the proportion of its students who graduate in 4 years is 82%. Larson/Farber 4 th ed. 29

Solution: Interpreting a Decision • The claim is represented by H 0. • If you reject H 0 you should conclude “there is sufficient evidence to indicate that the university’s claim is false. ” • If you fail to reject H 0, you should conclude “there is insufficient evidence to indicate that the university’s claim (of a four-year graduation rate of 82%) is false. ” Larson/Farber 4 th ed. 30

Example: Interpreting a Decision You perform a hypothesis test for the following claim. How should you interpret your decision if you reject H 0? If you fail to reject H 0? 2. Ha (Claim): Consumer Reports states that the mean stopping distance (on a dry surface) for a Honda Civic is less than 136 feet. Solution: • The claim is represented by Ha. • H 0 is “the mean stopping distance…is greater than or equal to 136 feet. ” Larson/Farber 4 th ed. 31

Solution: Interpreting a Decision • If you reject H 0 you should conclude “there is enough evidence to support Consumer Reports’ claim that the stopping distance for a Honda Civic is less than 136 feet. ” • If you fail to reject H 0, you should conclude “there is not enough evidence to support Consumer Reports’ claim that the stopping distance for a Honda Civic is less than 136 feet. ” Larson/Farber 4 th ed. 32

Steps for Hypothesis Testing 1. State the claim mathematically and verbally. Identify the null and alternative hypotheses. H 0: ? Ha : ? 2. Specify the level of significance. This sampling distribution is based on the assumption α= ? that H 0 is true. 3. Determine the standardized sampling distribution and draw its graph. z 0 4. Calculate the test statistic and its standardized value. Add it to your sketch. z 0 Test statistic Larson/Farber 4 th ed. 33

Steps for Hypothesis Testing 5. Find the P-value. 6. Use the following decision rule. Is the P-value less than or equal to the level of significance? No Fail to reject H 0. Yes Reject H 0. 7. Write a statement to interpret the decision in the context of the original claim. Larson/Farber 4 th ed. 34

Section 7. 1 Summary • Stated a null hypothesis and an alternative hypothesis • Identified type I and type I errors and interpreted the level of significance • Determined whether to use a one-tailed or two-tailed statistical test and found a p-value • Made and interpreted a decision based on the results of a statistical test • Wrote a claim for a hypothesis test Larson/Farber 4 th ed. 35

Section 7. 2 Hypothesis Testing for the Mean (Large Samples) Larson/Farber 4 th ed. 36

Section 7. 2 Objectives • Find P-values and use them to test a mean μ • Use P-values for a z-test • Find critical values and rejection regions in a normal distribution • Use rejection regions for a z-test Larson/Farber 4 th ed. 37

Using P-values to Make a Decision Rule Based on P-value • To use a P-value to make a conclusion in a hypothesis test, compare the P-value with . 1. If P , then reject H 0. 2. If P > , then fail to reject H 0. Larson/Farber 4 th ed. 38

Example: Interpreting a P-value The P-value for a hypothesis test is P = 0. 0237. What is your decision if the level of significance is 1. 0. 05? Solution: Because 0. 0237 < 0. 05, you should reject the null hypothesis. 2. 0. 01? Solution: Because 0. 0237 > 0. 01, you should fail to reject the null hypothesis. Larson/Farber 4 th ed. 39

Finding the P-value After determining the hypothesis test’s standardized test statistic and the test statistic’s corresponding area, do one of the following to find the P-value. a. For a left-tailed test, P = (Area in left tail). b. For a right-tailed test, P = (Area in right tail). c. For a two-tailed test, P = 2(Area in tail of test statistic). Larson/Farber 4 th ed. 40

Example: Finding the P-value Find the P-value for a left-tailed hypothesis test with a test statistic of z = -2. 23. Decide whether to reject H 0 if the level of significance is α = 0. 01. Solution: For a left-tailed test, P = (Area in left tail) P = 0. 0129 -2. 23 0 z Because 0. 0129 > 0. 01, you should fail to reject H 0 Larson/Farber 4 th ed. 41

Example: Finding the P-value Find the P-value for a two-tailed hypothesis test with a test statistic of z = 2. 14. Decide whether to reject H 0 if the level of significance is α = 0. 05. Solution: For a two-tailed test, P = 2(Area in tail of test statistic) 1 – 0. 9838 = 0. 0162 0. 9838 0 2. 14 P = 2(0. 0162) = 0. 0324 z Because 0. 0324 < 0. 05, you should reject H 0 Larson/Farber 4 th ed. 42

Z-Test for a Mean μ • Can be used when the population is normal and is known, or for any population when the sample size n is at least 30. • The test statistic is the sample mean • The standardized test statistic is z • When n 30, the sample standard deviation s can be substituted for . Larson/Farber 4 th ed. 43

Using P-values for a z-Test for Mean μ In Words 1. State the claim mathematically and verbally. Identify the null and alternative hypotheses. 2. Specify the level of significance. In Symbols State H 0 and Ha. Identify . 3. Determine the standardized test statistic. 4. Find the area that corresponds to z. Larson/Farber 4 th ed. Use Table 4 in Appendix B. 44

Using P-values for a z-Test for Mean μ In Words In Symbols 5. Find the P-value. a. For a left-tailed test, P = (Area in left tail). b. For a right-tailed test, P = (Area in right tail). c. For a two-tailed test, P = 2(Area in tail of test statistic). Reject H 0 if P-value 6. Make a decision to reject or is less than or equal fail to reject the null hypothesis. to . Otherwise, fail to reject H 0. 7. Interpret the decision in the context of the original claim. Larson/Farber 4 th ed. 45

Example: Hypothesis Testing Using Pvalues In an advertisement, a pizza shop claims that its mean delivery time is less than 30 minutes. A random selection of 36 delivery times has a sample mean of 28. 5 minutes and a standard deviation of 3. 5 minutes. Is there enough evidence to support the claim at = 0. 01? Use a P-value. Larson/Farber 4 th ed. 46

Solution: Hypothesis Testing Using Pvalues • • H 0: μ ≥ 30 min Ha: μ < 30 min = 0. 01 Test Statistic: • P-value 0. 0051 -2. 57 0 z • Decision: 0. 0051 < 0. 01 Reject H 0 At the 1% level of significance, you have sufficient evidence to conclude the mean delivery time is less than 30 minutes. Larson/Farber 4 th ed. 47
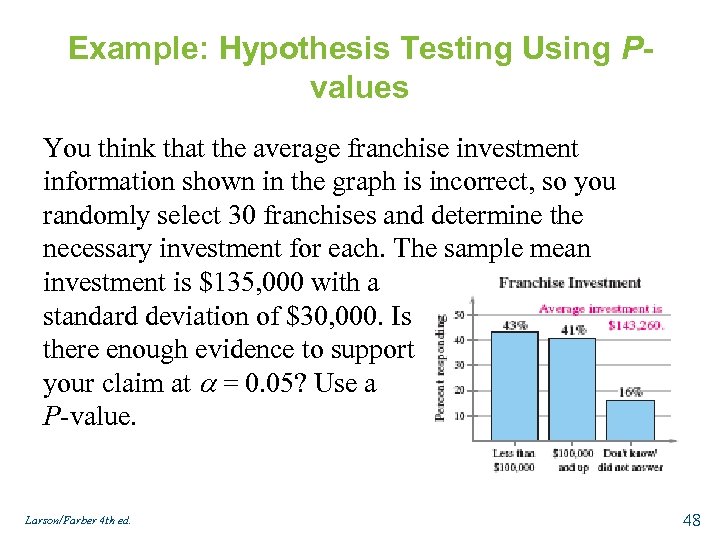
Example: Hypothesis Testing Using Pvalues You think that the average franchise investment information shown in the graph is incorrect, so you randomly select 30 franchises and determine the necessary investment for each. The sample mean investment is $135, 000 with a standard deviation of $30, 000. Is there enough evidence to support your claim at = 0. 05? Use a P-value. Larson/Farber 4 th ed. 48

Solution: Hypothesis Testing Using Pvalues • • H 0: μ = $143, 260 Ha: μ ≠ $143, 260 = 0. 05 Test Statistic: Larson/Farber 4 th ed. • P-value P = 2(0. 0655) = 0. 1310 0. 0655 -1. 51 0 z • Decision: 0. 1310 > 0. 05 Fail to reject H 0 At the 5% level of significance, there is not sufficient evidence to conclude the mean franchise investment is different from $143, 260. 49

Rejection Regions and Critical Values Rejection region (or critical region) • The range of values for which the null hypothesis is not probable. • If a test statistic falls in this region, the null hypothesis is rejected. • A critical value z 0 separates the rejection region from the nonrejection region. Larson/Farber 4 th ed. 50

Rejection Regions and Critical Values Finding Critical Values in a Normal Distribution 1. Specify the level of significance . 2. Decide whether the test is left-, right-, or two-tailed. 3. Find the critical value(s) z 0. If the hypothesis test is a. left-tailed, find the z-score that corresponds to an area of , b. right-tailed, find the z-score that corresponds to an area of 1 – , c. two-tailed, find the z-score that corresponds to ½ and 1 – ½. 4. Sketch the standard normal distribution. Draw a vertical line at each critical value and shade the rejection region(s). Larson/Farber 4 th ed. 51

Example: Finding Critical Values Find the critical value and rejection region for a twotailed test with = 0. 05. Solution: 1 – α = 0. 95 ½α = 0. 025 z 0 -z 0 = -1. 96 ½α = 0. 025 0 z 0 =z 0 1. 96 z The rejection regions are to the left of -z 0 = -1. 96 and to the right of z 0 = 1. 96. Larson/Farber 4 th ed. 52

Decision Rule Based on Rejection Region To use a rejection region to conduct a hypothesis test, calculate the standardized test statistic, z. If the standardized test statistic 1. is in the rejection region, then reject H 0. 2. is not in the rejection region, then fail to reject H 0. Fail to reject Ho. Fail to reject H 0. Reject H 0. z < z 0 Reject Ho. z 0 Fail to reject H 0 Left-Tailed Test Reject H 0 z < -z 0 0 0 z > z 0 z Right-Tailed Test Reject H 0 z z 0 z > z 0 Two-Tailed Test Larson/Farber 4 th ed. 53

Using Rejection Regions for a z-Test for a Mean μ In Words 1. State the claim mathematically and verbally. Identify the null and alternative hypotheses. 2. Specify the level of significance. In Symbols State H 0 and Ha. Identify . 3. Sketch the sampling distribution. 4. Determine the critical value(s). 5. Determine the rejection region(s). Larson/Farber 4 th ed. Use Table 4 in Appendix B. 54

Using Rejection Regions for a z-Test for a Mean μ In Words In Symbols 6. Find the standardized test statistic. 7. Make a decision to reject or fail to reject the null hypothesis. 8. Interpret the decision in the context of the original claim. Larson/Farber 4 th ed. If z is in the rejection region, reject H 0. Otherwise, fail to reject H 0. 55

Example: Testing with Rejection Regions Employees in a large accounting firm claim that the mean salary of the firm’s accountants is less than that of its competitor’s, which is $45, 000. A random sample of 30 of the firm’s accountants has a mean salary of $43, 500 with a standard deviation of $5200. At α = 0. 05, test the employees’ claim. Larson/Farber 4 th ed. 56

Solution: Testing with Rejection Regions • • H 0: μ ≥ $45, 000 Ha: μ < $45, 000 = 0. 05 Rejection Region: • Test Statistic 0. 05 -1. 645 0 -1. 58 Larson/Farber 4 th ed. z • Decision: Fail to reject H 0 At the 5% level of significance, there is not sufficient evidence to support the employees’ claim that the mean salary is less than $45, 000. 57

Example: Testing with Rejection Regions The U. S. Department of Agriculture reports that the mean cost of raising a child from birth to age 2 in a rural area is $10, 460. You believe this value is incorrect, so you select a random sample of 900 children (age 2) and find that the mean cost is $10, 345 with a standard deviation of $1540. At α = 0. 05, is there enough evidence to conclude that the mean cost is different from $10, 460? (Adapted from U. S. Department of Agriculture Center for Nutrition Policy and Promotion) Larson/Farber 4 th ed. 58

Solution: Testing with Rejection Regions • • H 0: μ = $10, 460 Ha: μ ≠ $10, 460 = 0. 05 Rejection Region: 0. 025 -1. 96 -2. 24 Larson/Farber 4 th ed. • Test Statistic 0. 025 0 1. 96 z • Decision: Reject H 0 At the 5% level of significance, you have enough evidence to conclude the mean cost of raising a child from birth to age 2 in a rural area is significantly different from $10, 460. 59

Section 7. 2 Summary • Found P-values and used them to test a mean μ • Used P-values for a z-test • Found critical values and rejection regions in a normal distribution • Used rejection regions for a z-test Larson/Farber 4 th ed. 60

Section 7. 3 Hypothesis Testing for the Mean (Small Samples) Larson/Farber 4 th ed. 61

Section 7. 3 Objectives • Find critical values in a t-distribution • Use the t-test to test a mean μ • Use technology to find P-values and use them with a t -test to test a mean μ Larson/Farber 4 th ed. 62

Finding Critical Values in a t-Distribution 1. Identify the level of significance . 2. Identify the degrees of freedom d. f. = n – 1. 3. Find the critical value(s) using Table 5 in Appendix B in the row with n – 1 degrees of freedom. If the hypothesis test is a. left-tailed, use “One Tail, ” column with a negative sign, b. right-tailed, use “One Tail, ” column with a positive sign, c. two-tailed, use “Two Tails, ” column with a negative and a positive sign. Larson/Farber 4 th ed. 63

Example: Finding Critical Values for t Find the critical value t 0 for a left-tailed test given = 0. 05 and n = 21. Solution: • The degrees of freedom are d. f. = n – 1 = 21 – 1 = 20. • Look at α = 0. 05 in the “One Tail, ” column. • Because the test is lefttailed, the critical value is negative. Larson/Farber 4 th ed. 0. 05 -1. 725 0 t 64

Example: Finding Critical Values for t Find the critical values t 0 and -t 0 for a two-tailed test given = 0. 05 and n = 26. Solution: • The degrees of freedom are d. f. = n – 1 = 26 – 1 = 25. • Look at α = 0. 05 in the “Two Tail, ” column. • Because the test is twotailed, one critical value is negative and one is positive. Larson/Farber 4 th ed. 0. 025 -2. 060 0 0. 025 2. 060 t 65

t-Test for a Mean μ (n < 30, Unknown) t-Test for a Mean • A statistical test for a population mean. • The t-test can be used when the population is normal or nearly normal, is unknown, and n < 30. • The test statistic is the sample mean • The standardized test statistic is t. • The degrees of freedom are d. f. = n – 1. Larson/Farber 4 th ed. 66

Using the t-Test for a Mean μ (Small Sample) In Words 1. State the claim mathematically and verbally. Identify the null and alternative hypotheses. In Symbols State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Identify the degrees of freedom and sketch the sampling distribution. d. f. = n – 1. 4. Determine any critical value(s). Use Table 5 in Appendix B. Larson/Farber 4 th ed. 67

Using the t-Test for a Mean μ (Small Sample) In Words In Symbols 5. Determine any rejection region(s). 6. Find the standardized test statistic. 7. Make a decision to reject or fail to reject the null hypothesis. 8. Interpret the decision in the context of the original claim. Larson/Farber 4 th ed. If t is in the rejection region, reject H 0. Otherwise, fail to reject H 0. 68

Example: Testing μ with a Small Sample A used car dealer says that the mean price of a 2005 Honda Pilot LX is at least $23, 900. You suspect this claim is incorrect and find that a random sample of 14 similar vehicles has a mean price of $23, 000 and a standard deviation of $1113. Is there enough evidence to reject the dealer’s claim at α = 0. 05? Assume the population is normally distributed. (Adapted from Kelley Blue Book) Larson/Farber 4 th ed. 69

Solution: Testing μ with a Small Sample • • • H 0: μ ≥ $23, 900 Ha: μ < $23, 900 α = 0. 05 df = 14 – 1 = 13 Rejection Region: • Test Statistic: • Decision: Reject H 0 0. 05 -1. 771 0 -3. 026 Larson/Farber 4 th ed. t At the 0. 05 level of significance, there is enough evidence to reject the claim that the mean price of a 2005 Honda Pilot LX is at least $23, 900 70

Example: Testing μ with a Small Sample An industrial company claims that the mean p. H level of the water in a nearby river is 6. 8. You randomly select 19 water samples and measure the p. H of each. The sample mean and standard deviation are 6. 7 and 0. 24, respectively. Is there enough evidence to reject the company’s claim at α = 0. 05? Assume the population is normally distributed. Larson/Farber 4 th ed. 71

Solution: Testing μ with a Small Sample • • • H 0: μ = 6. 8 Ha: μ ≠ 6. 8 α = 0. 05 df = 19 – 1 = 18 Rejection Region: 0. 025 -2. 101 0 0. 025 2. 101 • Test Statistic: • Decision: Fail to reject H 0 At the 0. 05 level of significance, there is not enough evidence to reject the claim that the mean p. H is 6. 8. t -1. 816 Larson/Farber 4 th ed. 72

Example: Using P-values with t-Tests The American Automobile Association claims that the mean daily meal cost for a family of four traveling on vacation in Florida is $118. A random sample of 11 such families has a mean daily meal cost of $128 with a standard deviation of $20. Is there enough evidence to reject the claim at α = 0. 10? Assume the population is normally distributed. (Adapted from American Automobile Association) Larson/Farber 4 th ed. 73
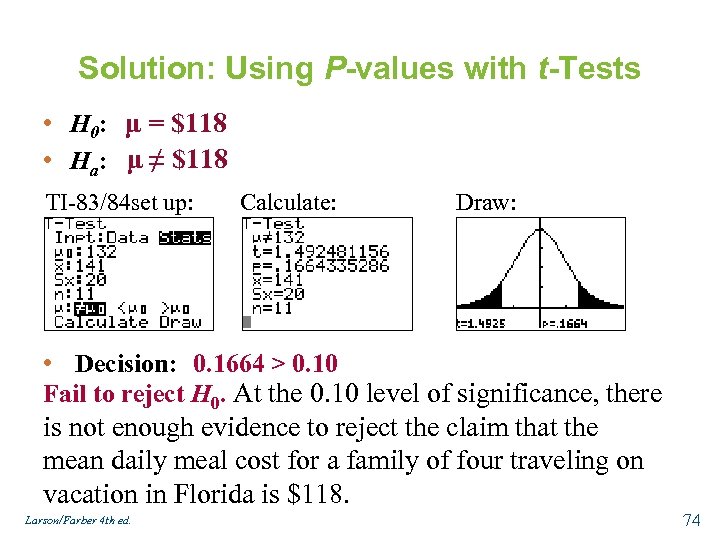
Solution: Using P-values with t-Tests • H 0: μ = $118 • Ha: μ ≠ $118 TI-83/84 set up: Calculate: Draw: • Decision: 0. 1664 > 0. 10 Fail to reject H 0. At the 0. 10 level of significance, there is not enough evidence to reject the claim that the mean daily meal cost for a family of four traveling on vacation in Florida is $118. Larson/Farber 4 th ed. 74

Section 7. 3 Summary • Found critical values in a t-distribution • Used the t-test to test a mean μ • Used technology to find P-values and used them with a t-test to test a mean μ Larson/Farber 4 th ed. 75

Section 7. 4 Hypothesis Testing for Proportions Larson/Farber 4 th ed. 76

Section 7. 4 Objectives • Use the z-test to test a population proportion p Larson/Farber 4 th ed. 77

z-Test for a Population Proportion • A statistical test for a population proportion. • Can be used when a binomial distribution is given such that np 5 and nq 5. • The test statistic is the sample proportion. • The standardized test statistic is z. Larson/Farber 4 th ed. 78

Using a z-Test for a Proportion p Verify that np ≥ 5 and nq ≥ 5 In Words 1. State the claim mathematically and verbally. Identify the null and alternative hypotheses. 2. Specify the level of significance. In Symbols State H 0 and Ha. Identify . 3. Sketch the sampling distribution. 4. Determine any critical value(s). Larson/Farber 4 th ed. Use Table 5 in Appendix B. 79

Using a z-Test for a Proportion p In Words In Symbols 5. Determine any rejection region(s). 6. Find the standardized test statistic. 7. Make a decision to reject or fail to reject the null hypothesis. 8. Interpret the decision in the context of the original claim. Larson/Farber 4 th ed. If z is in the rejection region, reject H 0. Otherwise, fail to reject H 0. 80

Example: Hypothesis Test for Proportions Zogby International claims that 45% of people in the United States support making cigarettes illegal within the next 5 to 10 years. You decide to test this claim and ask a random sample of 200 people in the United States whether they support making cigarettes illegal within the next 5 to 10 years. Of the 200 people, 49% support this law. At α = 0. 05 is there enough evidence to reject the claim? Solution: • Verify that np ≥ 5 and nq ≥ 5. np = 200(0. 45) = 90 and nq = 200(0. 55) = 110 Larson/Farber 4 th ed. 81

Solution: Hypothesis Test for Proportions • • H 0: p = 0. 45 Ha: p ≠ 0. 45 = 0. 05 Rejection Region: 0. 025 -1. 96 0. 025 0 1. 96 1. 14 Larson/Farber 4 th ed. • Test Statistic z • Decision: Fail to reject H 0 At the 5% level of significance, there is not enough evidence to reject the claim that 45% of people in the U. S. support making cigarettes illegal within the next 5 to 10 years. 82

Example: Hypothesis Test for Proportions The Pew Research Center claims that more than 55% of U. S. adults regularly watch their local television news. You decide to test this claim and ask a random sample of 425 adults in the United States whether they regularly watch their local television news. Of the 425 adults, 255 respond yes. At α = 0. 05 is there enough evidence to support the claim? Solution: • Verify that np ≥ 5 and nq ≥ 5. np = 425(0. 55) ≈ 234 and nq = 425 (0. 45) ≈ 191 Larson/Farber 4 th ed. 83

Solution: Hypothesis Test for Proportions • • H 0: p ≤ 0. 55 Ha: p > 0. 55 = 0. 05 Rejection Region: • Test Statistic 0. 05 0 1. 645 2. 07 Larson/Farber 4 th ed. z • Decision: Reject H 0 At the 5% level of significance, there is enough evidence to support the claim that more than 55% of U. S. adults regularly watch their local television news. 84

Section 7. 4 Summary • Used the z-test to test a population proportion p Larson/Farber 4 th ed. 85

Section 7. 5 Hypothesis Testing for Variance and Standard Deviation Larson/Farber 4 th ed. 86

Section 7. 5 Objectives • Find critical values for a χ2 -test • Use the χ2 -test to test a variance or a standard deviation Larson/Farber 4 th ed. 87

Finding Critical Values for the χ2 -Test 1. Specify the level of significance . 2. Determine the degrees of freedom d. f. = n – 1. 3. The critical values for the χ2 -distribution are found in Table 6 of Appendix B. To find the critical value(s) for a a. right-tailed test, use the value that corresponds to d. f. and . b. left-tailed test, use the value that corresponds to d. f. and 1 – . c. two-tailed test, use the values that corresponds to d. f. and ½ and d. f. and 1 – ½. Larson/Farber 4 th ed. 88
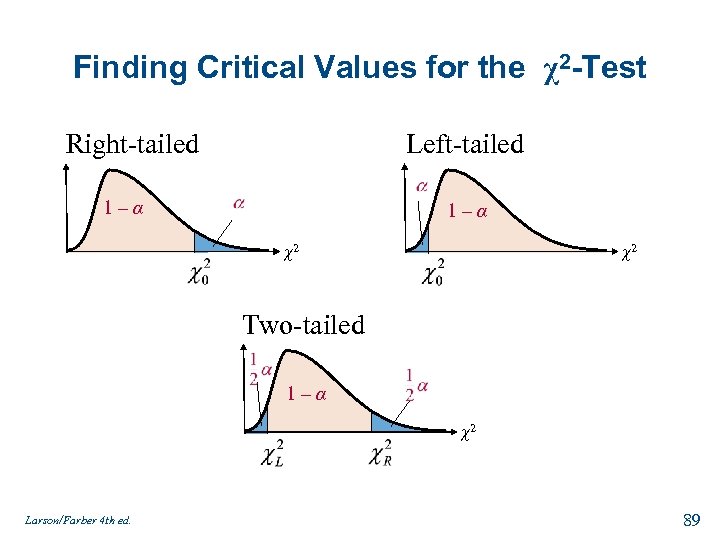
Finding Critical Values for the χ2 -Test Right-tailed Left-tailed 1–α χ2 χ2 Two-tailed 1–α χ2 Larson/Farber 4 th ed. 89

Example: Finding Critical Values for χ2 Find the critical χ2 -value for a left-tailed test when n = 11 and = 0. 01. Solution: • Degrees of freedom: n – 1 = 11 – 1 = 10 d. f. • The area to the right of the critical value is 1 – = 1 – 0. 01 = 0. 99. χ2 From Table 6, the critical value is Larson/Farber 4 th ed. . 90

Example: Finding Critical Values for χ2 Find the critical χ2 -value for a two-tailed test when n = 13 and = 0. 01. Solution: • Degrees of freedom: n – 1 = 13 – 1 = 12 d. f. • The areas to the right of the critical values are χ2 From Table 6, the critical values are Larson/Farber 4 th ed. and 91

The Chi-Square Test χ2 -Test for a Variance or Standard Deviation • A statistical test for a population variance or standard deviation. • Can be used when the population is normal. • The test statistic is s 2. • The standardized test statistic follows a chi-square distribution with degrees of freedom d. f. = n – 1. Larson/Farber 4 th ed. 92

Using the χ2 -Test for a Variance or Standard Deviation In Words 1. State the claim mathematically and verbally. Identify the null and alternative hypotheses. In Symbols State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Determine the degrees of freedom and sketch the sampling distribution. d. f. = n – 1 4. Determine any critical value(s). Larson/Farber 4 th ed. Use Table 6 in Appendix B. 93

Using the χ2 -Test for a Variance or Standard Deviation In Words In Symbols 5. Determine any rejection region(s). 6. Find the standardized test statistic. 7. Make a decision to reject or fail to reject the null hypothesis. 8. Interpret the decision in the context of the original claim. Larson/Farber 4 th ed. If χ2 is in the rejection region, reject H 0. Otherwise, fail to reject H 0. 94

Example: Hypothesis Test for the Population Variance A dairy processing company claims that the variance of the amount of fat in the whole milk processed by the company is no more than 0. 25. You suspect this is wrong and find that a random sample of 41 milk containers has a variance of 0. 27. At α = 0. 05, is there enough evidence to reject the company’s claim? Assume the population is normally distributed. Larson/Farber 4 th ed. 95

Solution: Hypothesis Test for the Population Variance • • • H 0: σ2 ≤ 0. 25 Ha: σ2 > 0. 25 α = 0. 05 df = 41 – 1 = 40 Rejection Region: 55. 758 43. 2 Larson/Farber 4 th ed. χ2 • Test Statistic: • Decision: Fail to Reject H 0 At the 5% level of significance, there is not enough evidence to reject the company’s claim that the variance of the amount of fat in the whole milk is no more than 0. 25. 96

Example: Hypothesis Test for the Standard Deviation A restaurant claims that the standard deviation in the length of serving times is less than 2. 9 minutes. A random sample of 23 serving times has a standard deviation of 2. 1 minutes. At α = 0. 10, is there enough evidence to support the restaurant’s claim? Assume the population is normally distributed. Larson/Farber 4 th ed. 97
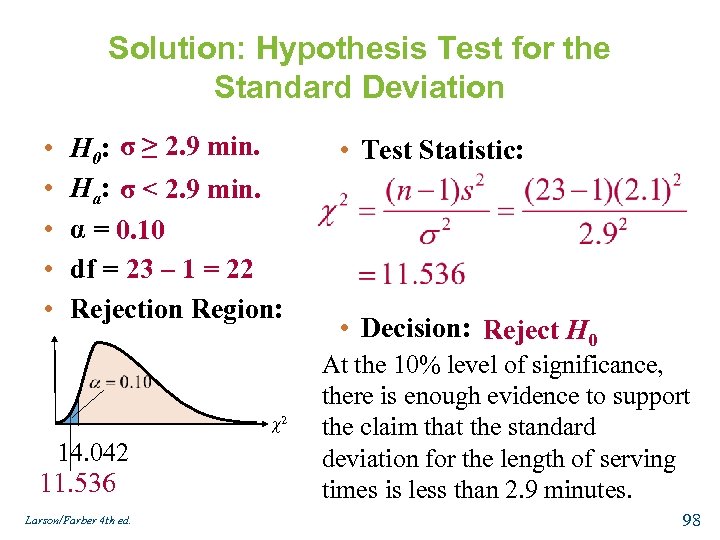
Solution: Hypothesis Test for the Standard Deviation • • • H 0: σ ≥ 2. 9 min. Ha: σ < 2. 9 min. α = 0. 10 df = 23 – 1 = 22 Rejection Region: χ2 14. 042 11. 536 Larson/Farber 4 th ed. • Test Statistic: • Decision: Reject H 0 At the 10% level of significance, there is enough evidence to support the claim that the standard deviation for the length of serving times is less than 2. 9 minutes. 98

Example: Hypothesis Test for the Population Variance A sporting goods manufacturer claims that the variance of the strength in a certain fishing line is 15. 9. A random sample of 15 fishing line spools has a variance of 21. 8. At α = 0. 05, is there enough evidence to reject the manufacturer’s claim? Assume the population is normally distributed. Larson/Farber 4 th ed. 99

Solution: Hypothesis Test for the Population Variance • • • H 0: σ2 = 15. 9 Ha: σ2 ≠ 15. 9 α = 0. 05 df = 15 – 1 = 14 Rejection Region: χ2 5. 629 26. 119 19. 194 Larson/Farber 4 th ed. • Test Statistic: • Decision: Fail to Reject H 0 At the 5% level of significance, there is not enough evidence to reject the claim that the variance in the strength of the fishing line is 15. 9. 100

Section 7. 5 Summary • Found critical values for a χ2 -test • Used the χ2 -test to test a variance or a standard deviation Larson/Farber 4 th ed. 101
f7b38784faea46dc8e523271081321e0.ppt