d8a02a62df0233a6349bc0a5f18da8ea.ppt
- Количество слайдов: 47

Chapter 7: Document Preprocessing (textbook) • Document preprocessing is a procedure which can be divided mainly into five text operations (or transformations): (1) Lexical analysis of the text with the objective of treating digits, hyphens, punctuation marks, and the case of letters. (2) Elimination of stop-words with the objective of filtering out words with very low discrimination values for retrieval purposes.

Document Preprocessing (3) Stemming of the remaining words with the objective of removing affixes (i. e. , prefixes and suffixes) and allowing the retrieval of documents containing syntactic variations of query terms (e. g. , connecting, connected, etc). (4) Selection of index terms to determine which words/stems (or groups of words) will be used as an indexing elements. Usually, the decision on whether a particular word will be used as an index term is related to the syntactic nature of the word. In fact , noun words frequently carry more semantics than adjectives, adverbs, and verbs.

Document Preprocessing (5) Construction of term categorization structures such as a thesaurus, or extraction of structure directly represented in the text, for allowing the expansion of the original query with related terms (a usually useful procedure).

Lexical Analysis of the text Task: convert strings of characters into sequence of words. • Main task is to deal with spaces, e. g, multiple spaces are treated as one space. • Digits—ignoring numbers is a common way. Special cases, 1999, 2000 standing for specific years are important. Mixed digits are important, e. g. , 510 B. C. 16 digits numbers might be credit card #. • Hyphens: state-of-the art and “state of the art” should be treated as the same. • Punctuation marks: remove them. Exception: 510 B. C • Lower or upper case of letters: treated as the same. • Many exceptions: semi-automatic.

Elimination of Stopwords • words appear too often are not useful for IR. • Stopwords: words appear more than 80% of the documents in the collection are stopwords and are filtered out as potential index words.

Stemming • A Stem: the portion of a word which is left after the removal of its affixes (i. e. , prefixes or suffixes). • Example: connect is the stem for {connected, connecting connection, connections} • Porter algorithm: using suffix list for suffix stripping. S , sses ss, etc.

Index terms selection • Identification of noun groups • Treat nouns appear closely as a single component, e. g. , computer science

Thesaurus • Thesaurus: a precompiled list of important words in a given domain of knowledge and for each word in this list, there is a set of related words. • Vocabulary control in an information retrieval system • Thesaurus construction – Manual construction – Automatic construction

Vocabulary control • Standard vocabulary for both indexing and searching (for the constructors of the system and the users of the system)

Objectives of vocabulary control • To promote the consistent representation of subject matter by indexers and searchers , thereby avoiding the dispersion of related materials. • To facilitate the conduct of a comprehensive search on some topic by linking together terms whose meanings are related paradigmatically.

Thesaurus • Not like common dictionary – Words with their explanations • May contain words in a language • Or only contains words in a specific domain. • With a lot of other information especially the relationship between words – Classification of words in the language – Words relationship like synonyms, antonyms

On-Line Thesaurus • http: //www. thesaurus. com • http: //www. dictionary. com/ • http: //www. cogsci. princeton. edu/~wn/

Dictionary vs. Thesaurus Check Information use http: //www. thesaurus. com Dictionary • in·for·ma·tion ( n f r-m sh n) n. – Knowledge derived from study, experience, or instruction. – Knowledge of specific events or situations that has been gathered or received by communication; intelligence or news. See Synonyms at knowledge. –. . . Thesaurus [Nouns] information, enlightenment, acquaintance …… [Verbs] tell; inform, inform of; acquaint, acquaint with; impart, …… [Adjectives] informed; reported; published

Use of Thesaurus • To control the term used in indexing , for a specific domain only use the terms in thesaurus as indexing terms • Assist the users to form proper queries by the help information contained in thesaurus

Construction of Thesaurus • Stemming can be used for reduce the size of thesaurus • Can be constructed either manually or automatically

Word. Net: manually constructed • Word. Net® is an online lexical reference system whose design is inspired by current psycholinguistic theories of human lexical memory. English nouns, verbs, adjectives and adverbs are organized into synonym sets, each representing one underlying lexical concept. Different relations link the synonym sets.

Relations in Word. Net

Automatic Thesaurus Construction • A variety of methods can be used in construction thesaurus • Term similarity can be used for constructing thesaurus

Complete Term Relation Method Term 1 Term 2 Term 3 Term 4 Term 5 Term 6 Term 7 Term 8 Doc 1 0 4 0 0 0 2 1 3 Doc 2 3 1 4 3 1 2 0 1 Doc 3 3 0 0 0 3 0 Doc 4 0 1 0 3 0 0 2 0 Doc 5 2 2 2 3 1 4 0 2 n. Term – Document Relationship can be calculated using a variety of methods n. Like tf-idf n. Term similarity can be calculated base on the term – document relationship n for example:

Complete Term Relation Method Term 1 Term 3 Term 4 Term 5 Term 6 Term 7 Term 8 7 Term 1 Term 2 16 15 14 14 9 7 8 12 3 18 6 17 18 6 16 0 8 6 18 6 9 3 2 16 Term 2 7 Term 3 16 8 Term 4 15 12 18 Term 5 14 3 6 6 Term 6 14 18 16 18 6 Term 7 9 6 0 6 9 2 Term 8 7 17 8 9 3 16 Set threshold to 10 3 3

Complete Term Relation Method T 3 T 1 Group u. T 1, T 3, T 4, T 6 T 2 u. T 1, T 5 T 4 u. T 2, T 4, T 6 T 5 u. T 2, T 6, T 8 u. T 7 T 6 T 8 T 7

Indexing • Arrangement of data (data structure) to permit fast searching • Which list is easier to search? sow fox pig eel yak hen ant cat dog hog ant cat dog eel fox hen hog pig sow yak

Creating inverted files Word Extraction Word IDs Original Documents W 1: d 1, d 2, d 3 W 2: d 2, d 4, d 7, d 9 Document IDs Wn : di, …dn Inverted Files

Creating Inverted file • Map the file names to file IDs • Consider the following Original Documents D 1 The Department of Computer Science was established in 1984. D 2 The Department launched its first BSc(Hons) in Computer Studies in 1987. D 3 followed by the MSc in Computer Science which was started in 1991. D 4 The Department also produced its first Ph. D graduate in 1994. D 5 Our staff have contributed intellectually and professionally to the advancements in these fields.

Creating Inverted file Red: stop word D 1 The Department of Computer Science was established in 1984. D 2 The Department launched its first BSc(Hons) in Computer Studies in 1987. D 3 followed by the MSc in Computer Science which was started in 1991. D 4 The Department also produced its first Ph. D graduate in 1994. D 5 Our staff have contributed intellectually and professionally to the advancements in these fields.

Creating Inverted file After stemming, make lowercase (option), delete numbers (option) D 1 depart comput scienc establish D 2 depart launch bsc hons comput studi D 3 follow msc comput scienc start D 4 depart produc phd graduat D 5 staff contribut intellectu profession advanc field

Creating Inverted file (unsorted) Words Documents depart d 1, d 2, d 4 produc d 4 comput d 1, d 2, d 3 phd d 4 scienc d 1, d 3 graduat d 4 establish d 1 staff d 5 launch d 2 contribut d 5 bsc d 2 intellectu d 5 hons d 2 profession d 5 studi d 2 advanc d 5 follow d 3 field d 5 msc d 3 start d 3
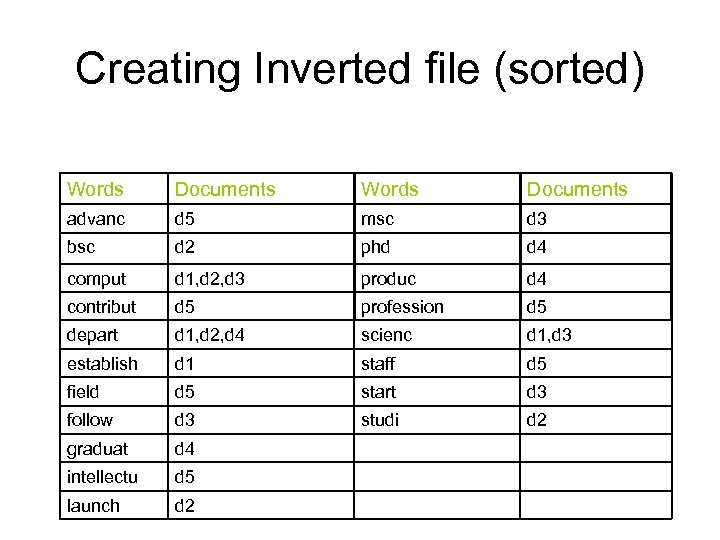
Creating Inverted file (sorted) Words Documents advanc d 5 msc d 3 bsc d 2 phd d 4 comput d 1, d 2, d 3 produc d 4 contribut d 5 profession d 5 depart d 1, d 2, d 4 scienc d 1, d 3 establish d 1 staff d 5 field d 5 start d 3 follow d 3 studi d 2 graduat d 4 intellectu d 5 launch d 2

Searching on Inverted File • Binary Search – Using in the small scale • Create thesaurus and combining techniques such as: – Hashing – B+tree – Pointer to the address in the indexed file

Huffman codes • Binary character code: each character is represented by a unique binary string. • A data file can be coded in two ways: a b c d e f frequency(% 45 13 12 16 9 5 ) fixed-length code 000 001 010 011 100 101 variable-length code first way The 0 101 100 111 110 needs 100 3=300 bits. The second way 1 0 needs 45 1+13 3+12 3+16 3+9 4+5 4=232 bits.

Variable-length code • Need some care to read the code. – 001011101 (codeword: a=0, b=00, c=01, d=11. ) – Where to cut? 00 can be explained as either aa or b. • Prefix of 0011: 0, 001, and 0011. • Prefix codes: no codeword is a prefix of some other codeword. (prefix free) • Prefix codes are simple to encode and decode.
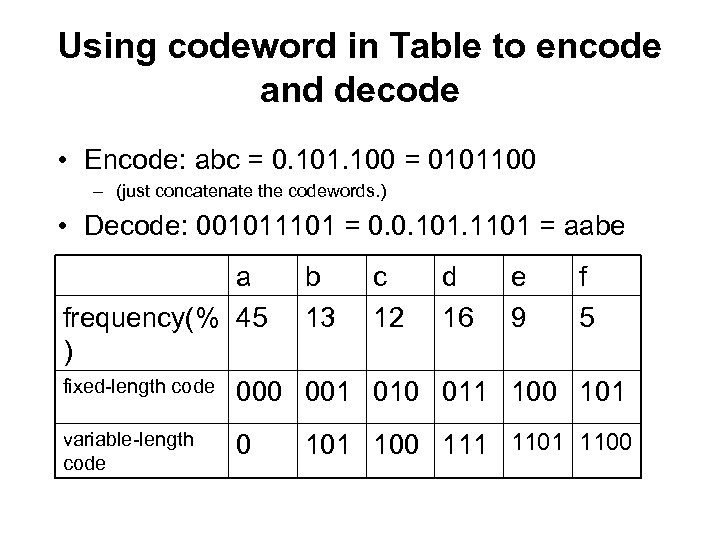
Using codeword in Table to encode and decode • Encode: abc = 0. 101. 100 = 0101100 – (just concatenate the codewords. ) • Decode: 001011101 = 0. 0. 101. 1101 = aabe a b c d e f frequency(% 45 13 12 16 9 5 ) fixed-length code 000 001 010 011 100 101 variable-length code 0 101 100 111 1100

• Encode: abc = 0. 101. 100 = 0101100 – (just concatenate the codewords. ) • Decode: 001011101 = 0. 0. 101. 1101 = aabe – (use the (right)binary tree below: ) 10 0 1 86 14 0 1 58 0 0 28 1 0 a: 4 b: 13 c: 1 5 Tree for the 2 fixed length codeword 1 0 d: 16 e: 9 a: 4 5 1 f: 5 1 0 0 14 10 0 c: 1 2 25 55 1 30 1 0 b: 13 14 d: 16 0 1 f: 5 e: 9 Tree for variable-length codeword 1

Binary tree • Every nonleaf node has two children. • The fixed-length code in our example is not optimal. • The total number of bits required to encode a file is – f ( c ) : the frequency (number of occurrences) of c in the file – d. T(c): denote the depth of c’s leaf in the tree

Constructing an optimal code • Formal definition of the problem: • Input: a set of characters C={c 1, c 2, …, cn}, each c C has frequency f[c]. • Output: a binary tree representing codewords so that the total number of bits required for the file is minimized. • Huffman proposed a greedy algorithm to solve the problem.

(a) (b) f: 5 c: 1 2 e: 9 c: 1 2 b: 13 0 1 f: 5 e: 9 a: 4 5 d: 16 14 d: 16 a: 4 5
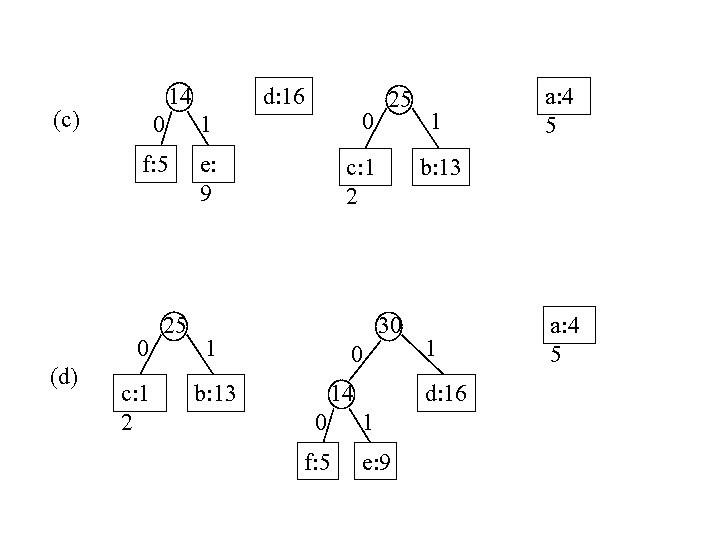
14 (c) d: 16 0 1 0 f: 5 e: 9 c: 1 2 0 (d) 25 c: 1 2 25 b: 13 30 1 0 b: 13 14 0 f: 5 1 a: 4 5 1 d: 16 1 e: 9 a: 4 5
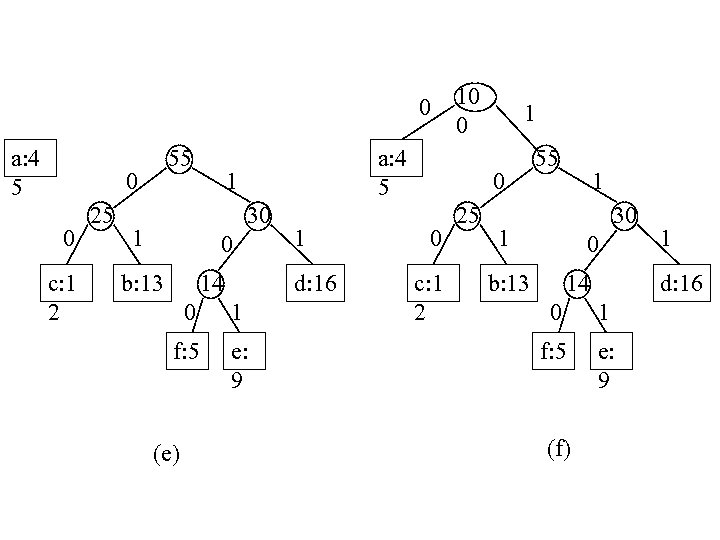
0 a: 4 5 55 0 0 c: 1 2 25 a: 4 5 1 30 1 0 14 b: 13 1 d: 16 0 1 f: 5 e: 9 (e) 10 0 1 0 0 c: 1 2 25 55 1 30 1 0 b: 13 14 d: 16 0 1 f: 5 e: 9 (f) 1

HUFFMAN(C) 1 n: =|C| 2 Q: =C 3 for i: =1 to n-1 do 4 z: =ALLOCATE_NODE() 5 x: =left[z]: =EXTRACT_MIN(Q) 6 y: =right[z]: =EXTRACT_MIN(Q) 7 f[z]: =f[x]+f[y] 8 INSERT(Q, z) 9 return EXTRACT_MIN(Q)

The Huffman Algorithm • This algorithm builds the tree T corresponding to the optimal code in a bottom-up manner. • C is a set of n characters, and each character c in C is a character with a defined frequency f[c]. • Q is a priority queue, keyed on f, used to identify the two least-frequent characters to merge together. • The result of the merger is a new object (internal node) whose frequency is the sum of the two objects.

Time complexity • Lines 4 -8 are executed n-1 times. • Each heap operation in Lines 4 -8 takes O(lg n) time. • Total time required is O(n lg n). Note: The details of heap operation will not be tested. Time complexity O(n lg n) should be remembered.

Another example: e: 4 c: 6 a: 6 c: 6 b: 9 d: 11 10 0 e: 4 d: 11 1 a: 6
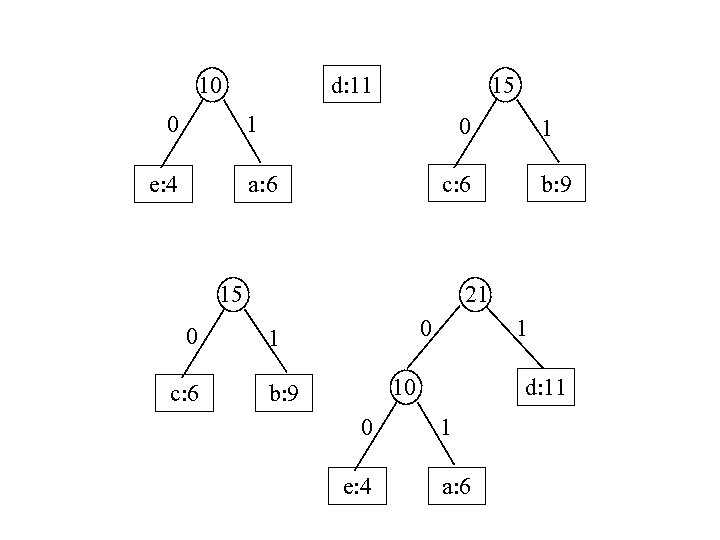
10 0 15 d: 11 1 e: 4 0 c: 6 a: 6 c: 6 b: 9 21 15 0 1 1 10 b: 9 0 e: 4 d: 11 1 a: 6
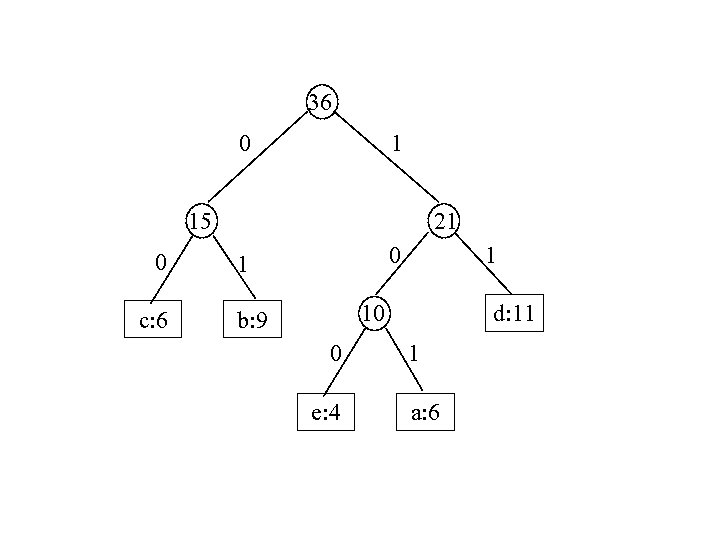
36 0 1 21 15 0 c: 6 0 1 1 10 b: 9 0 e: 4 d: 11 1 a: 6

Correctness of Huffman’s Greedy Algorithm (Fun Part, not required) • • • Again, we use our general strategy. Let x and y are the two characters in C having the lowest frequencies. (the first two characters selected in the greedy algorithm. ) We will show the two properties: 1. There exists an optimal solution Topt (binary tree representing codewords) such that x and y are siblings in Topt. 2. Let z be a new character with frequency f[z]=f[x]+f[y] and C’=C-{x, y} {z}. Let z be T’ an optimal tree for C’. Then we can get Topt from x y T’ by replacing z with
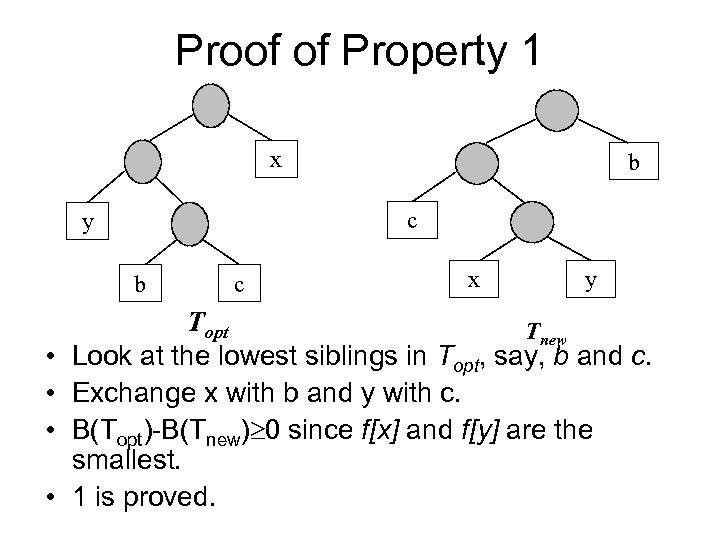
Proof of Property 1 x c y b • • b c x y Topt Tnew Look at the lowest siblings in Topt, say, b and c. Exchange x with b and y with c. B(Topt)-B(Tnew) 0 since f[x] and f[y] are the smallest. 1 is proved.
![2. Let z be a new character with frequency f[z]=f[x]+f[y] and C’=C-{x, y} {z}. 2. Let z be a new character with frequency f[z]=f[x]+f[y] and C’=C-{x, y} {z}.](https://present5.com/presentation/d8a02a62df0233a6349bc0a5f18da8ea/image-47.jpg)
2. Let z be a new character with frequency f[z]=f[x]+f[y] and C’=C-{x, y} {z}. Let T’ be an optimal tree for C’. Then we can get Topt from T’ by z replacing z with y x Proof: Let T be the tree obtained from T’ by replacing z with the three nodes. B(T)=B(T’)+f[x]+f[y]. … (1) (the length of the codes for x and y are 1 bit more than that of z. ) Now prove T= Topt by contradiction. If T Topt, then B(T)>B(Topt). …(2) From 1, x and y are siblings in Topt. Thus, we can delete x and y from Topt and get another tree T’’ for C’. B(T’’)=B(Topt) –f[x]-f[y]<B(T)-f[x]-f[y]=B(T’). using (2) using (1) Thus, T(T’’)<B(T’). Contradiction! --- T’ is optimum.
d8a02a62df0233a6349bc0a5f18da8ea.ppt