Chapter 7 Conceptual Data Modeling R Mc Fadyen

Chapter 7 Conceptual Data Modeling R Mc. Fadyen 92. 2911 7 -1

Topics l topics: – Developing a conceptual data model from use cases – UML notations for conceptual data modeling – UML class diagram bears a resemblance to an Entity Relationship Diagram (see 92. 3914 for ERDs) R Mc. Fadyen 92. 2911 2

Topics l UML: – attributes – association, aggregation, and generalization – multiplicities, roles, … R Mc. Fadyen 92. 2911 3

R Mc. Fadyen 92. 2911 4

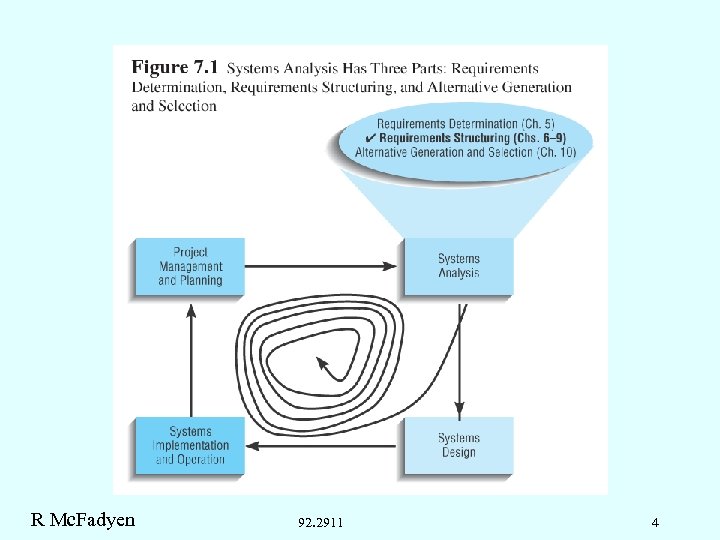
What Is a Conceptual Data Model? l A detailed model that shows the overall structure of organizational data; it is independent of any database management system or other implementation considerations. l Represented by UML class diagrams l Sources: • Current knowledge • Existing system • System documents / reports • Interviews • Use cases R Mc. Fadyen 92. 2911 5

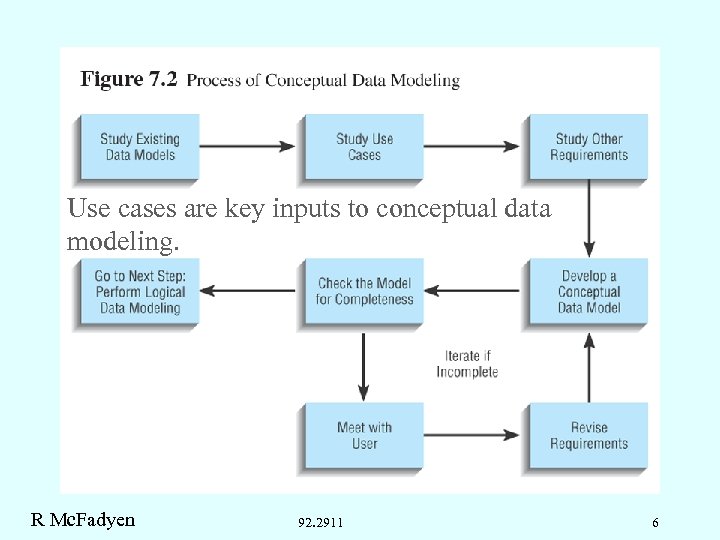Use cases are key inputs to conceptual data modeling. R Mc. Fadyen 92. 2911 6

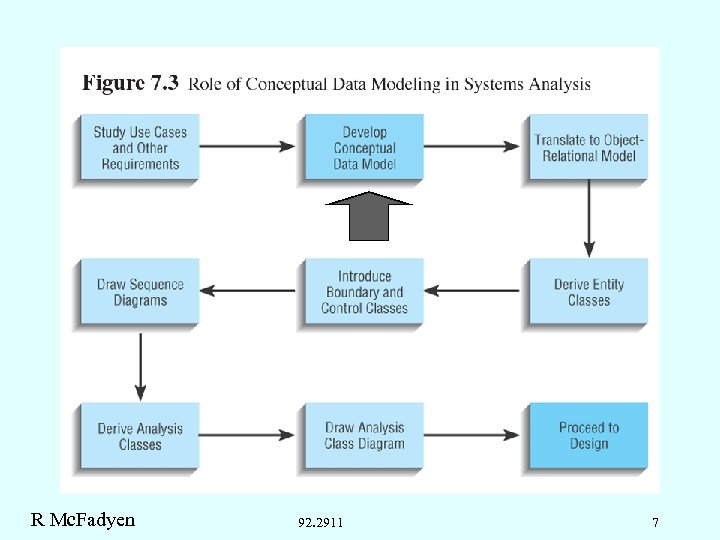R Mc. Fadyen 92. 2911 7

R Mc. Fadyen 92. 2911 8

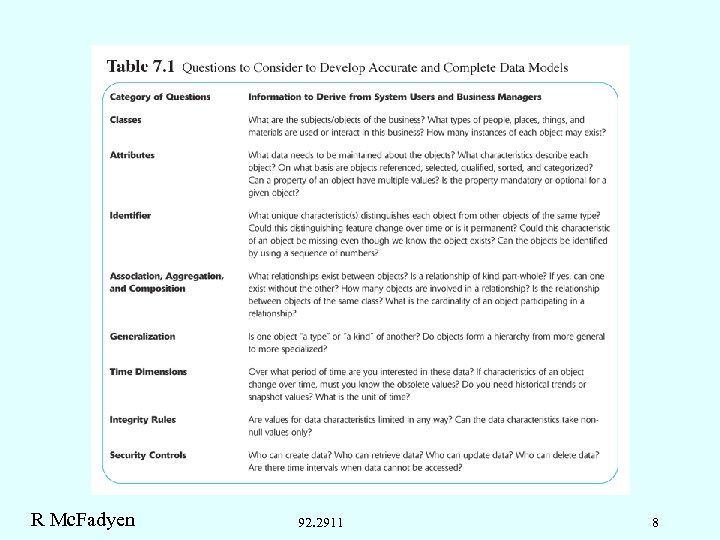
Conceptual Data Model Elements l l l l Classes Attributes Identifiers Associations, aggregations, compositions Generalizations Time dimensions Integrity rules Security controls R Mc. Fadyen 92. 2911 9

What Is an Object? l An entity that encapsulates data and behavior l Examples: product, employee, order, line item l Class – a set of objects that share the same attributes, operations, relationships, and semantics (abstract) l Instance – a single object (concrete) R Mc. Fadyen 92. 2911 10

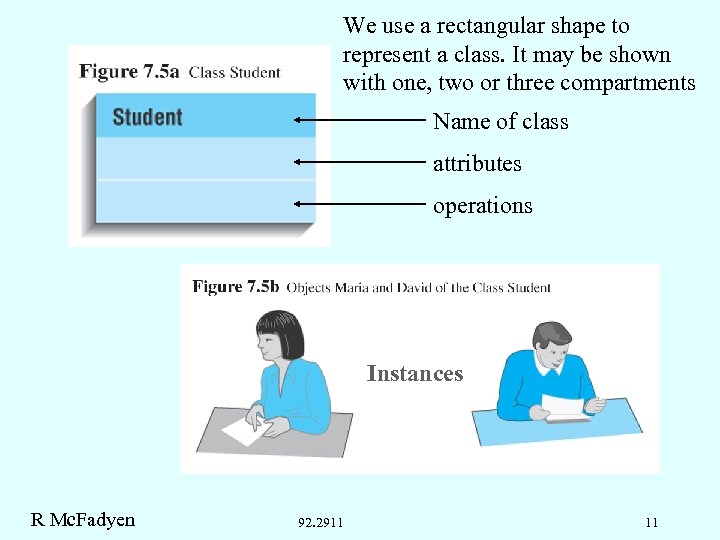We use a rectangular shape to represent a class. It may be shown with one, two or three compartments Name of class attributes operations Instances R Mc. Fadyen 92. 2911 11

R Mc. Fadyen 92. 2911 12

Types of Attributes l Simple attributes – contain single data item l Identifiers – unique key value l Multivalued attributes – contain multiple values simultaneously l Composite attributes – group of related attributes R Mc. Fadyen 92. 2911 13

Stereotypes in Class Diagrams • Stereotype – a construct that extends the UML vocabulary • Identifier stereotype <> for primary key • Multivalued stereotype <> R Mc. Fadyen 92. 2911 14

Primary key is a unique identifier; no two Student instances will have the same student. Id value. R Mc. Fadyen 92. 2911 15

Multivalued attribute can contain multiple values; a student may have several phone numbers R Mc. Fadyen 92. 2911 16

Composite attributes have multiple components. They are treated as separate classes in conceptual data models. The attribute address is defined to be of type Address. R Mc. Fadyen 92. 2911 17

What Is a Relationship? l A semantic connection between objects of one or more classes l In UML, represented as a line connecting two or more class boxes (or connecting one class to itself) l In UML, known as an association R Mc. Fadyen 92. 2911 18

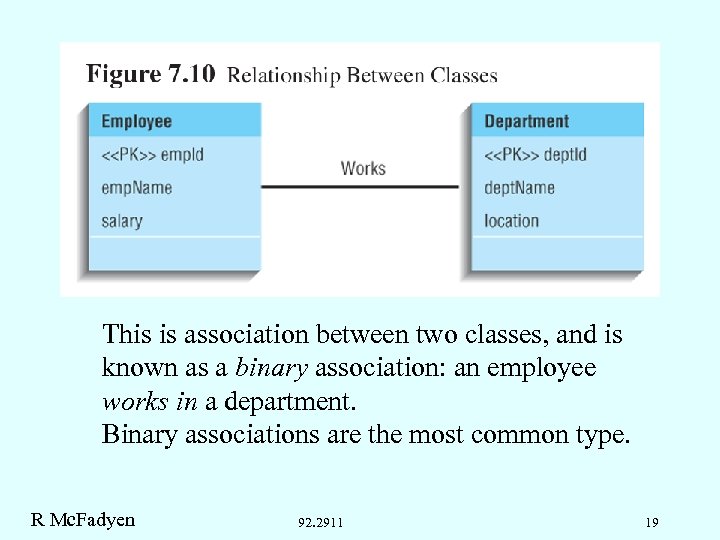This is association between two classes, and is known as a binary association: an employee works in a department. Binary associations are the most common type. R Mc. Fadyen 92. 2911 19

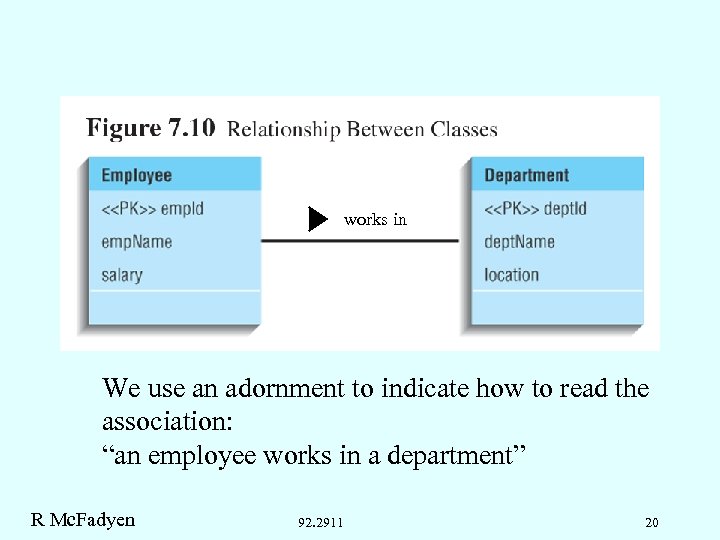works in We use an adornment to indicate how to read the association: “an employee works in a department” R Mc. Fadyen 92. 2911 20

Roles identify the purpose of each class in the relationship. • Rolenames are useful (much) later on when we have software classes with attributes referring to instances of classes • Note that neither class has an attribute referring to object(s) of the other class – that would be an implementation detail R Mc. Fadyen 92. 2911 21

What Is Relationship Degree? l The number of classes that participate in a relationship From text l Main degrees: – Unary – a relationship between objects of the same class – Binary – a relationship between objects of two different classes – Ternary – a relationship between objects of three different classes – !NOTE. Our text differs from other texts in these definitions: • Degree is the number of objects that participate – there is no Unary relationship. • Instead of unary, the term recursive is used R Mc. Fadyen 92. 2911 22

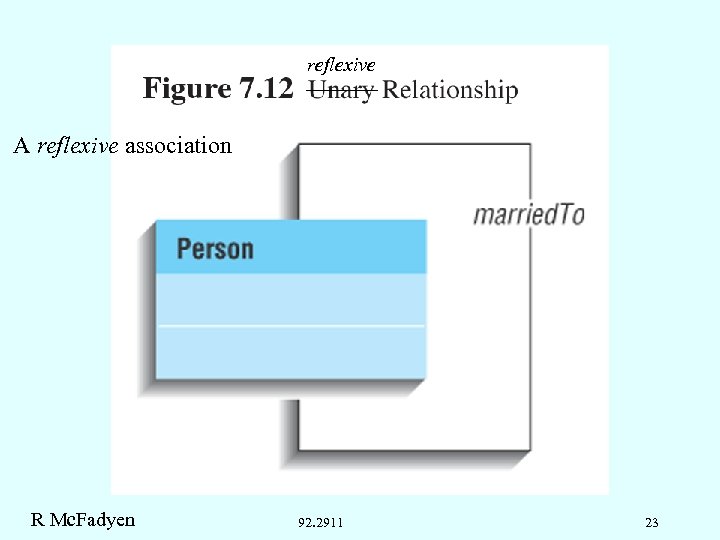reflexive A reflexive association R Mc. Fadyen 92. 2911 23

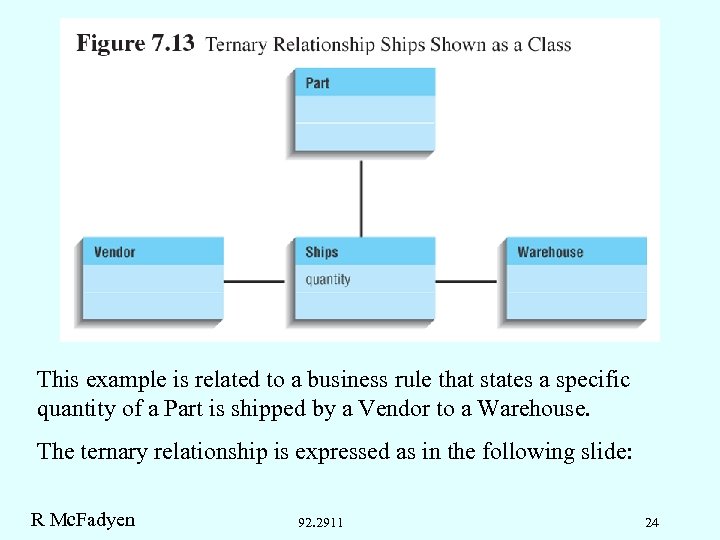This example is related to a business rule that states a specific quantity of a Part is shipped by a Vendor to a Warehouse. The ternary relationship is expressed as in the following slide: R Mc. Fadyen 92. 2911 24

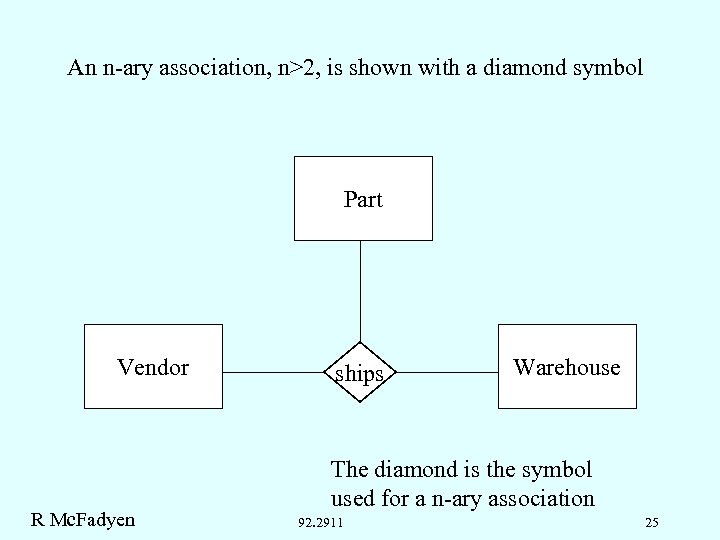An n-ary association, n>2, is shown with a diamond symbol Part Vendor R Mc. Fadyen ships Warehouse The diamond is the symbol used for a n-ary association 92. 2911 25

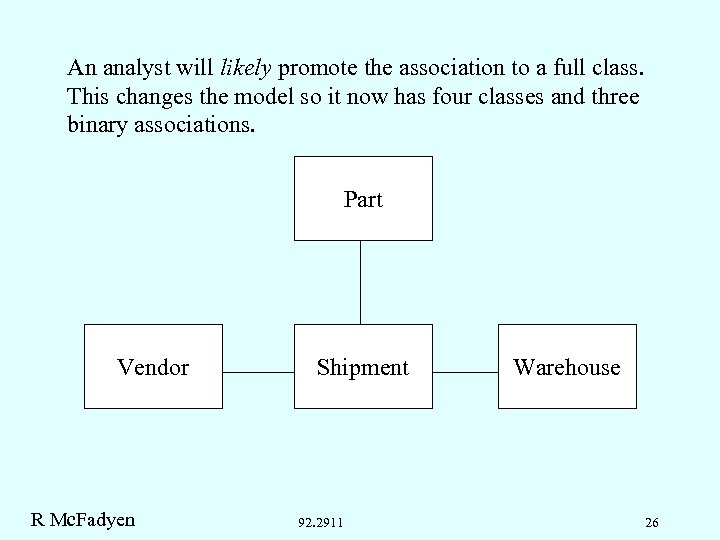An analyst will likely promote the association to a full class. This changes the model so it now has four classes and three binary associations. Part Vendor R Mc. Fadyen Shipment ships 92. 2911 Warehouse 26

Multiplicity l Associations can be: – One – to – one – One – to – many – Many – to – many R Mc. Fadyen 92. 2911 27

Multiplicity l The range of the number of objects in a class that can or must be associated with each object of another class in an association. l l l l * 0. . * 1. . 5 0, 1 1 3 R Mc. Fadyen * represents zero or more same meaning as above one or more one, two, three, four, or five zero or one exactly three 92. 2911 Ranges use. . Enumeration uses , 28

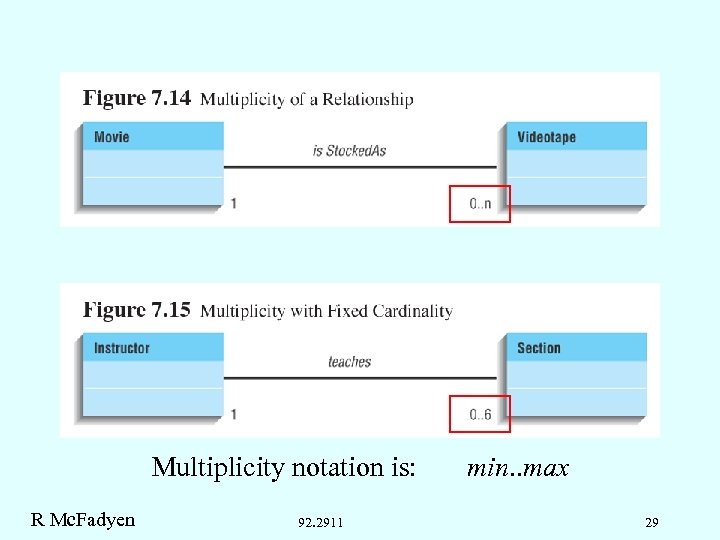Multiplicity notation is: R Mc. Fadyen 92. 2911 min. . max 29

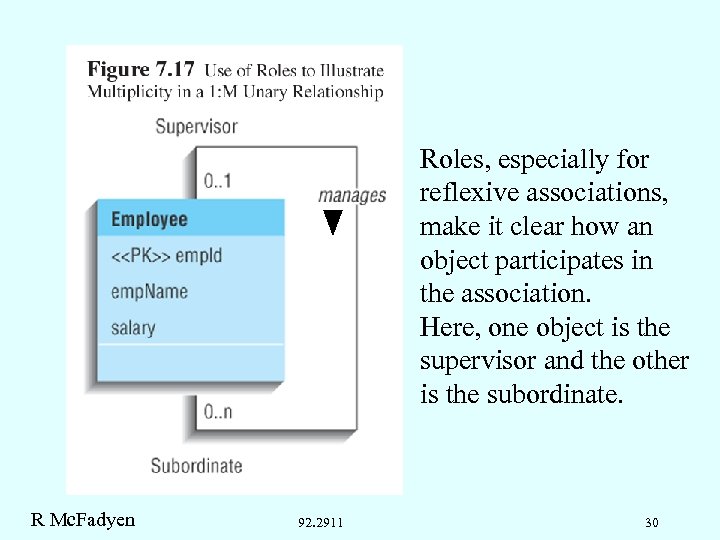Roles, especially for reflexive associations, make it clear how an object participates in the association. Here, one object is the supervisor and the other is the subordinate. R Mc. Fadyen 92. 2911 30

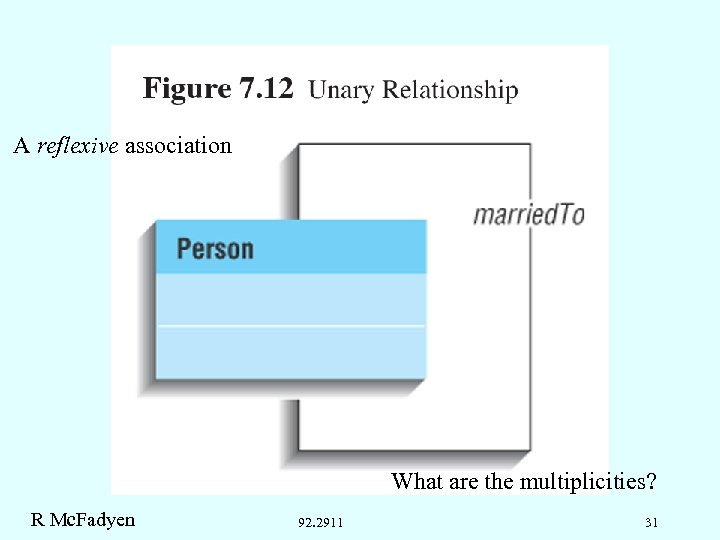A reflexive association What are the multiplicities? R Mc. Fadyen 92. 2911 31

Associative Class l An associative class is both a class and an association. It contains attributes and/or participates in relationships in its own right l Represented as a class connected to an association with a dotted line l Typically appears with a many-to-many association – there probably are attributes that describe the association R Mc. Fadyen 92. 2911 32

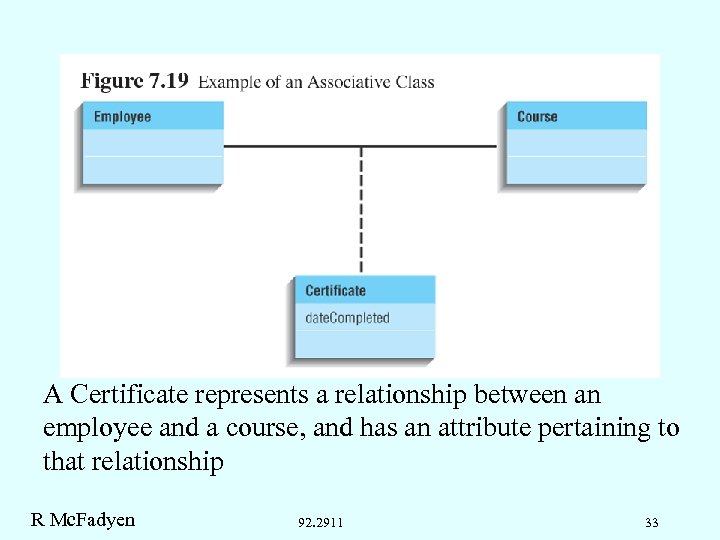A Certificate represents a relationship between an employee and a course, and has an attribute pertaining to that relationship R Mc. Fadyen 92. 2911 33

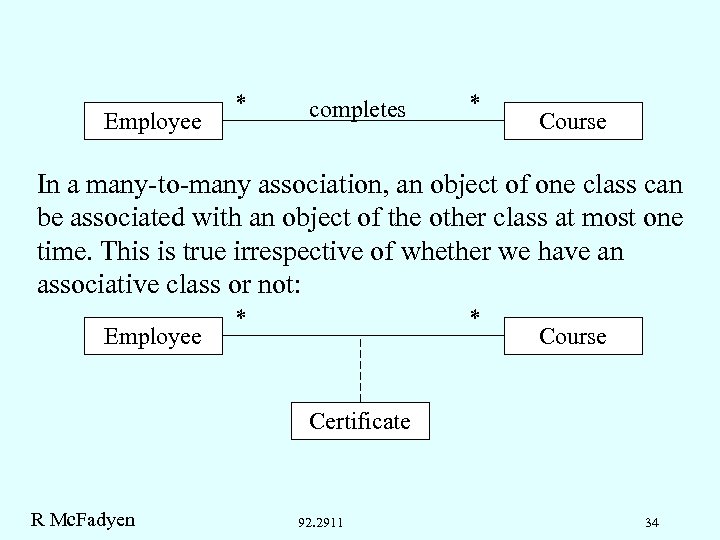Employee * completes * Course In a many-to-many association, an object of one class can be associated with an object of the other class at most one time. This is true irrespective of whether we have an associative class or not: Employee * * Course Certificate R Mc. Fadyen 92. 2911 34

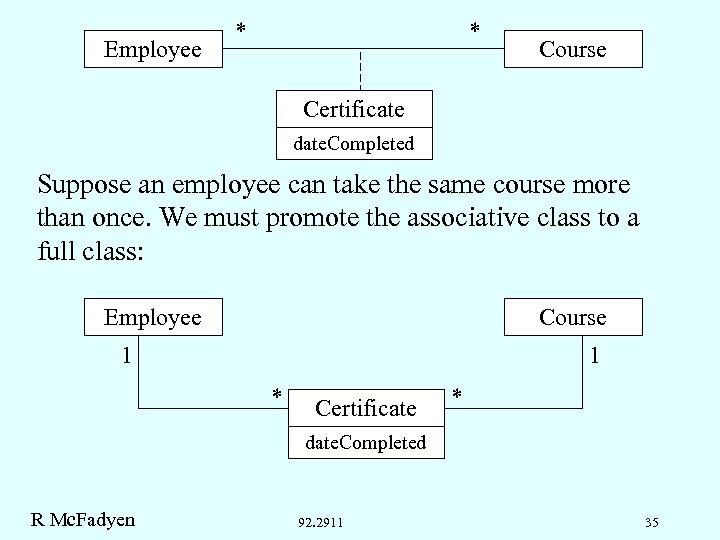Employee * * Course Certificate date. Completed Suppose an employee can take the same course more than once. We must promote the associative class to a full class: Employee Course 1 1 * Certificate * date. Completed R Mc. Fadyen 92. 2911 35

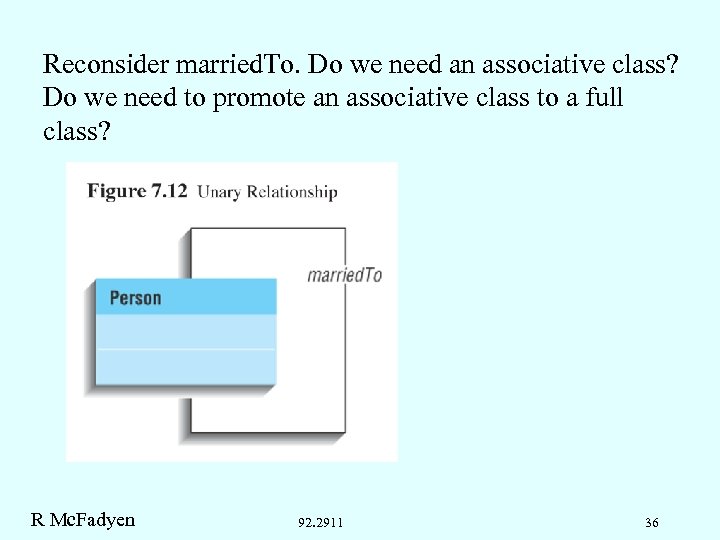Reconsider married. To. Do we need an associative class? Do we need to promote an associative class to a full class? R Mc. Fadyen 92. 2911 36

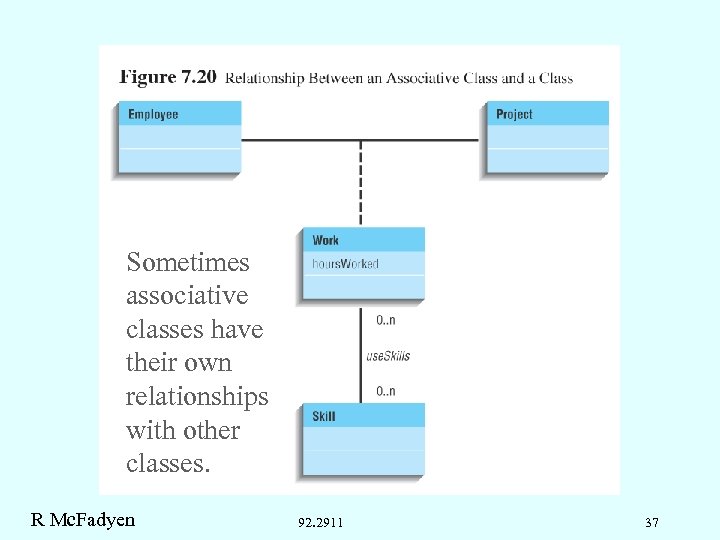Sometimes associative classes have their own relationships with other classes. R Mc. Fadyen 92. 2911 37

Types of Associations • Association – no object is subordinate to any other. • Aggregation – one class represents the whole, and the other represents the part, but there is no concept of ownership • Composition – one class represents the whole, and the other represents the part; the whole contains or owns the part; the part cannot exist without the whole. • Generalization/specialization –an association between a general thing (the superclass or parent class) and a more specific kind of thing (the subclass or child class) R Mc. Fadyen 92. 2911 38

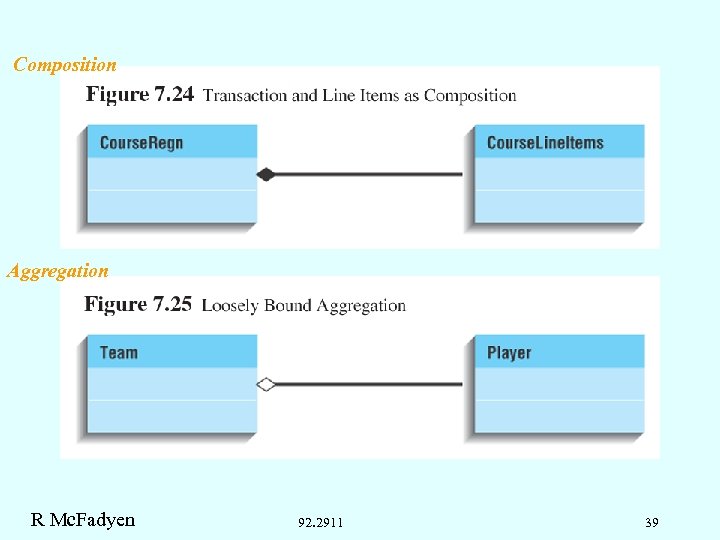Composition Aggregation R Mc. Fadyen 92. 2911 39

Generalization • a generalization is an association between a general thing (the superclass or parent class) and a more specific kind of thing (the subclass or child class) • Inheritance – A subclass inherits all the attributes and operations of its superclass; an instance of the subclass contains all the same information (plus more) as an instance of the superclass • An instance of a subclass is also an instance of the superclass R Mc. Fadyen 92. 2911 40

Generalization (Ch 26) Multiple subclasses can be grouped to indicate they are related subclasses Library. Member Staff. Member Student. Member It then becomes meaningful to consider certain constraints: complete, incomplete, disjoint, overlapping R Mc. Fadyen 92. 2911 41

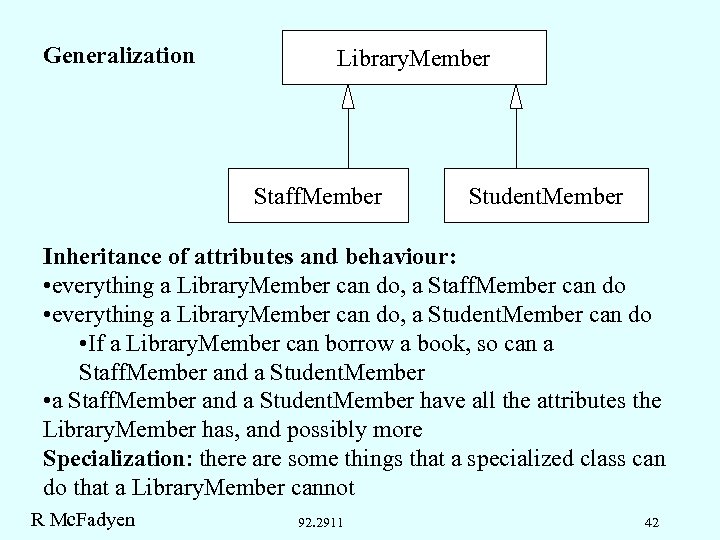Generalization Library. Member Staff. Member Student. Member Inheritance of attributes and behaviour: • everything a Library. Member can do, a Staff. Member can do • everything a Library. Member can do, a Student. Member can do • If a Library. Member can borrow a book, so can a Staff. Member and a Student. Member • a Staff. Member and a Student. Member have all the attributes the Library. Member has, and possibly more Specialization: there are some things that a specialized class can do that a Library. Member cannot R Mc. Fadyen 92. 2911 42

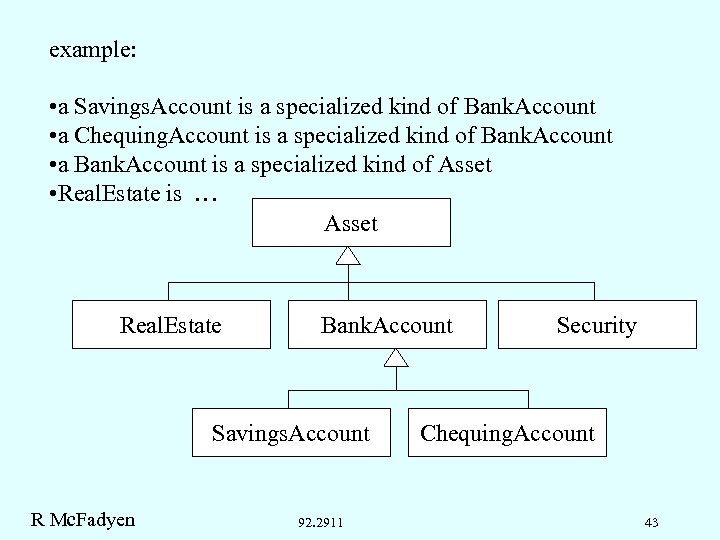example: • a Savings. Account is a specialized kind of Bank. Account • a Chequing. Account is a specialized kind of Bank. Account • a Bank. Account is a specialized kind of Asset • Real. Estate is … Asset Real. Estate Bank. Account Savings. Account R Mc. Fadyen 92. 2911 Security Chequing. Account 43

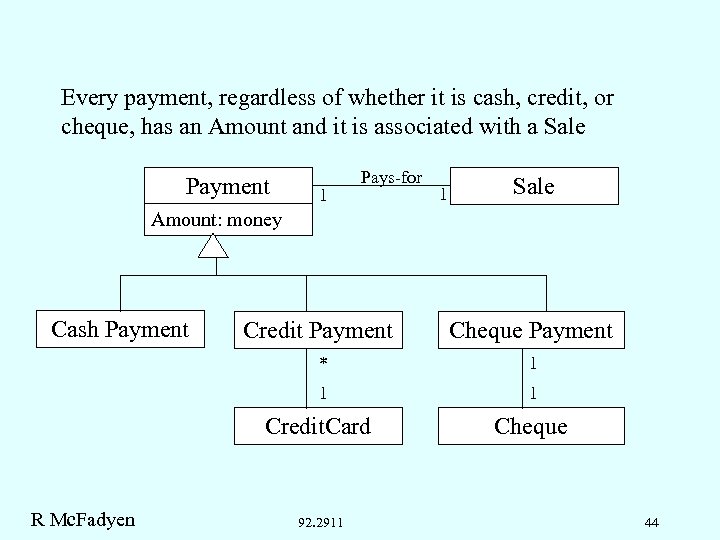Every payment, regardless of whether it is cash, credit, or cheque, has an Amount and it is associated with a Sale Payment 1 Pays-for 1 Sale Amount: money Cash Payment Credit Payment Cheque Payment * 1 1 1 Credit. Card R Mc. Fadyen 92. 2911 Cheque 44

Motivation for partitioning a conceptual class into subclasses: • subclass has additional attributes of interest • subclass has additional associations of interest • subclass is operated on, handled, reacted to, or manipulated differently than the superclass or other subclasses • the subclass concept represents an animate thing that behaves differently than the superclass or other subclasses R Mc. Fadyen 92. 2911 45

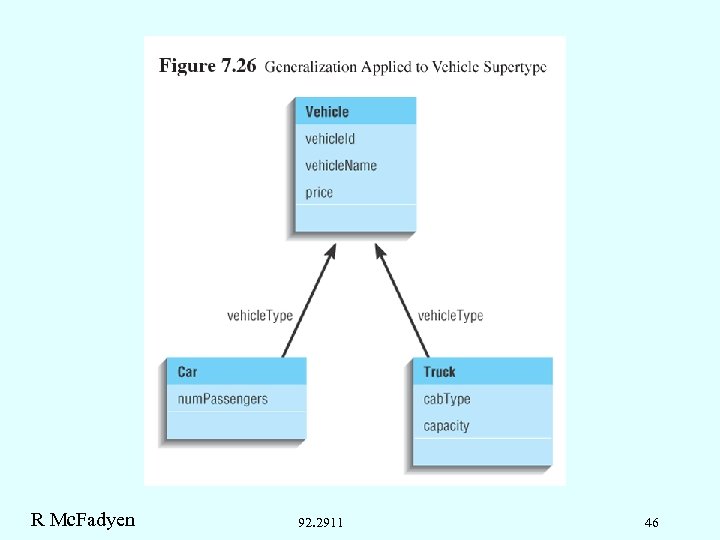R Mc. Fadyen 92. 2911 46

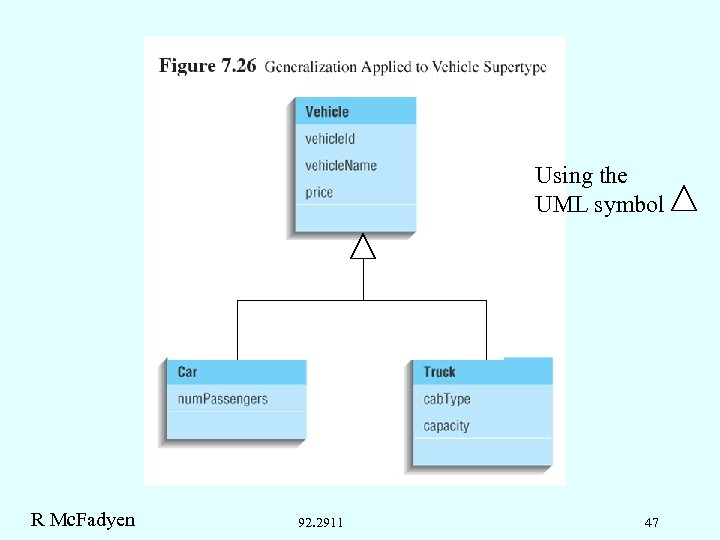Using the UML symbol R Mc. Fadyen 92. 2911 47

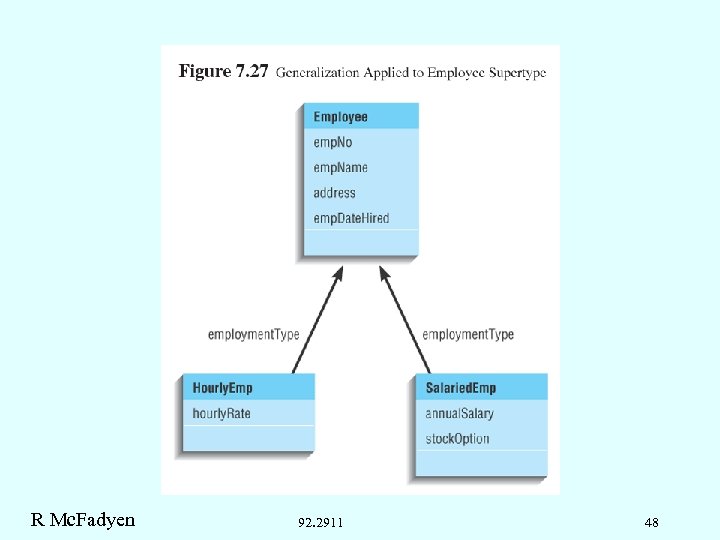R Mc. Fadyen 92. 2911 48

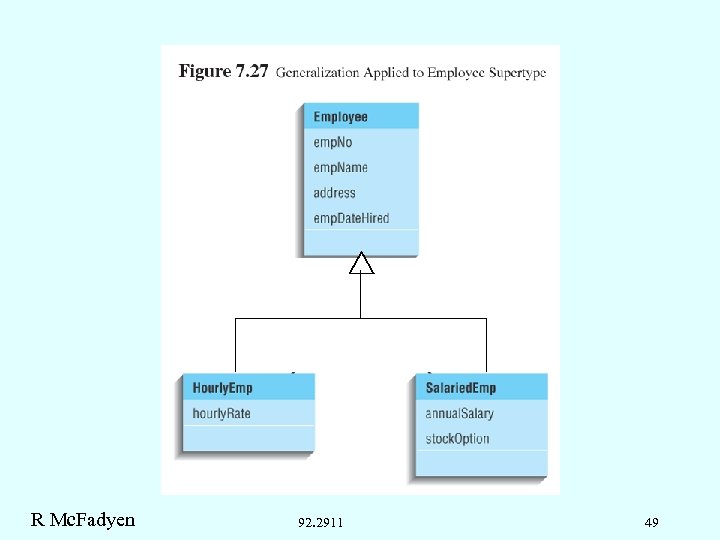R Mc. Fadyen 92. 2911 49

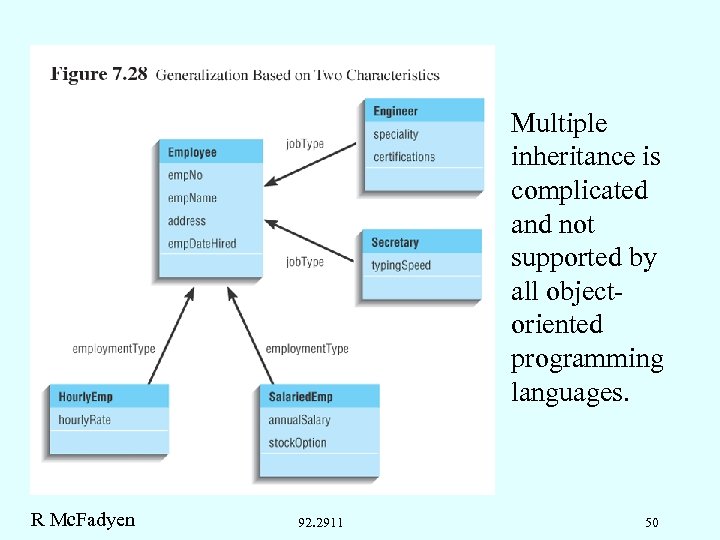Multiple inheritance is complicated and not supported by all objectoriented programming languages. R Mc. Fadyen 92. 2911 50

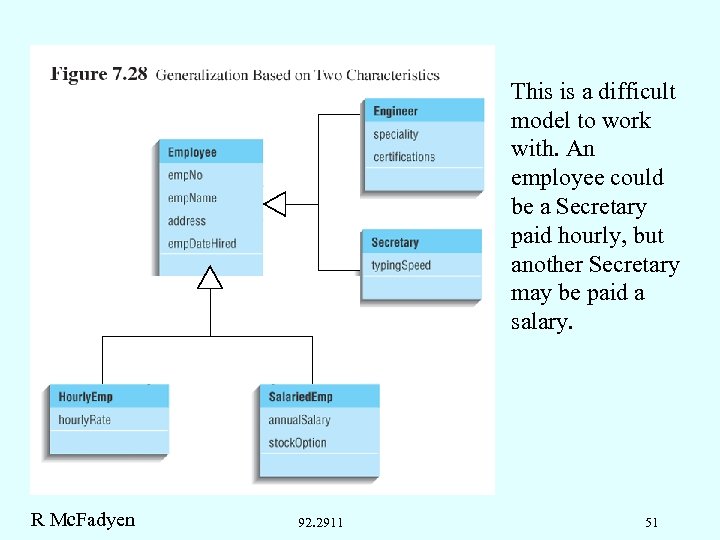This is a difficult model to work with. An employee could be a Secretary paid hourly, but another Secretary may be paid a salary. R Mc. Fadyen 92. 2911 51

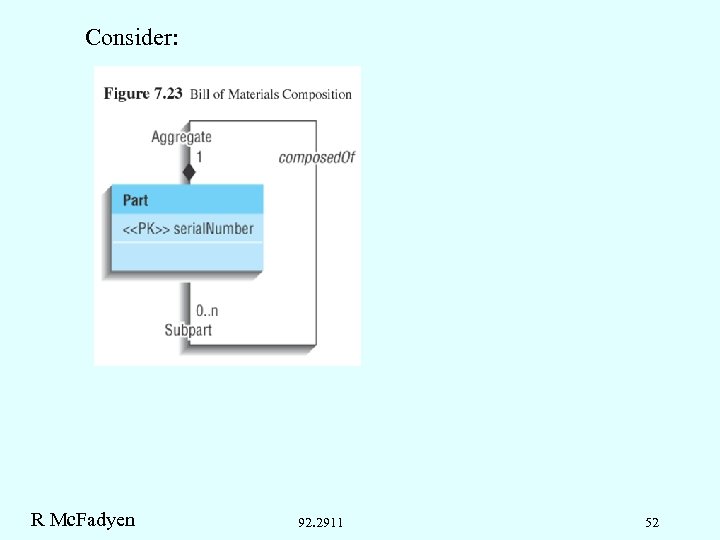Consider: R Mc. Fadyen 92. 2911 52

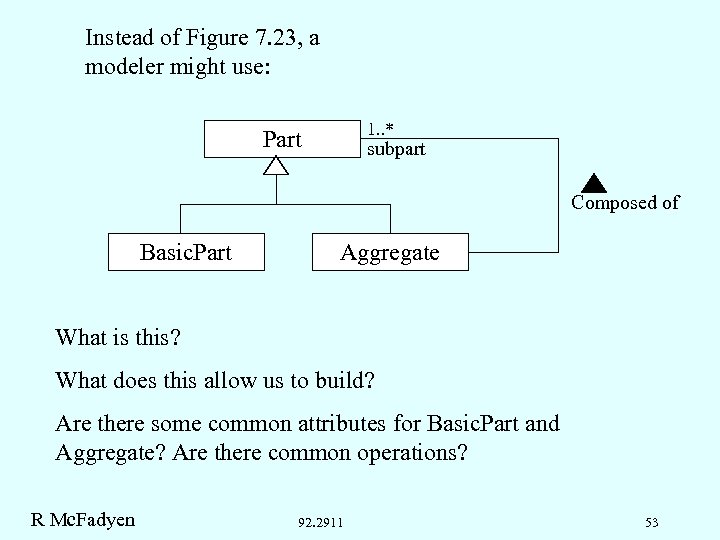Instead of Figure 7. 23, a modeler might use: 1. . * Part subpart Composed of Basic. Part Aggregate What is this? What does this allow us to build? Are there some common attributes for Basic. Part and Aggregate? Are there common operations? R Mc. Fadyen 92. 2911 53

Summary l We have covered: – – – Developing data models from use cases UML notation for conceptual modeling Associations and multiplicity Aggregation, composition, and generalization Attributes: identifier, composite, multivalued, derived attributes R Mc. Fadyen 92. 2911 54