4babeb0b9539f72e4efe88cc3049ff4e.ppt
- Количество слайдов: 25

Chapter 6 Rational Numbers and Proportional Reasoning Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

NCTM Standard: Proportional Reasoning Working with proportions is a major focus proposed in these Standards for the middle grades. Students should become proficient in creating ratios to make comparisons in situations that involve pairs of numbers, as in the following problem: If three packages of cocoa make fifteen cups of hot chocolate, how many packages are needed to make sixty cups? (p. 34) Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

6 -4 Ratios, Proportions, and Proportional Reasoning Proportions Scale Drawings Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Ratios A ratio is § used to compare quantities. § usually written a: b or . § used to represent part-to-part, part-to-whole, or whole-to-part comparisons. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -23 There were 7 males and 12 females in the Dew Drop Inn on Monday evening. In the game room next door were 14 males and 24 females. a. Express the number of males to females at the inn as a ratio (part-to-part). b. Express the number of males to females at the game room as a ratio (part-to-part). Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -23 (continued) There were 7 males and 12 females in the Dew Drop Inn on Monday evening. In the game room next door were 14 males and 24 females. c. Express the number of males in the game room to the number of people in the game room as a ratio (part-to-whole). Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Proportions A proportion is a statement that two given ratios are equal. If a, b, c, and d are all real numbers, and b ≠ 0 and d ≠ 0, then the proportion is true if, and only, if ad = bc. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Proportions Allie and Bente type at the same speed. Allie started typing first. When Allie had typed 8 pages, Bente had typed 4 pages. When Bente has typed 10 pages, how many has Allie typed? This is an example of an additive relationship. Students should reason that since the two people type at the same speed, when Bente has typed an additional 6 pages, Allie should have also typed an additional 6 pages, so she should have typed 8 + 6, or 14, pages. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Proportions Carl can type 8 pages for every 4 pages that Dan can type. If Dan has typed 12 pages, how many pages has Carl typed? This is an example of a multiplicative relationship. Since Carl types twice as fast as Dan he will type twice as many pages as Dan. Therefore, when Dan has typed 12 pages, Carl has typed 24 pages. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -24 If there are 3 cars for every 8 students at a high school, how many cars are there for 1200 students? There are 450 cars. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Definition Constant of Proportionality If the variables x and y are related by the equality y = kx, then y is proportional to x, and k is the constant of proportionality between y and x. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Definition A central idea in proportional reasoning is that a relationship between two quantities is such that the ratio of one quantity to the other remains unchanged as the numerical values of both quantities change. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Cross-Multiplication Method Principles and Standards (p. 221) points out the following concerning the cross-multiplication method of solving proportions. Instruction in solving proportions should include methods that have a strong intuitive basis. The socalled cross-multiplication method can be developed meaningfully if it arises naturally in students’ work, but it can also have unfortunate side effects when students do not adequately understand when the method is appropriate to use. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Cross-Multiplication Method Other approaches to solving proportions are often more intuitive and also quite powerful. For example, when trying to decide which is the better buy— 12 tickets for $15. 00 or 20 tickets for $23. 00 —students might choose to use a scaling strategy (finding the cost for a common number of tickets) or a unit-rate strategy (finding the cost for one ticket). (p. 221) Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Scaling Strategy Use the scaling strategy to determine which is the better buy — 12 tickets for $15 or 20 tickets for $23? The scaling strategy for solving the problem would involve finding the cost for a common number of tickets, the LCM(12, 20) = 60 Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Scaling Strategy In the first plan, since 12 tickets cost $15, then 60 tickets cost $75. In the second plan, since 20 tickets cost $23, then 60 tickets cost $69. The second plan is the better buy. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Unit-Rate Strategy Use the unit-rate strategy to determine which is the better buy — 12 tickets for $15 or 20 tickets for $23? The unit-rate strategy for solving this problem involves finding the cost of one ticket under each plan and then comparing the unit cost. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Unit-Rate Strategy In the first plan, since 12 tickets cost $15, then 1 ticket costs $1. 25. In the second plan, since 20 tickets cost $23, then 1 ticket costs $1. 15. The second plan is the better buy. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -25 Kai, Paulus, and Judy made $2520 for painting a house. Kai worked 30 hr, Paulus worked 50 hr, and Judy worked 60 hr. They divided the money in proportion to the number of hours worked. If they all earn the same rate of pay, how much did each earn? Let x be the unit rate or the rate of pay per hour. Then, 30 x denotes the amount of money that Kai received. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -25 (continued) Paulus received 50 x because then, and only then, will the ratios of the amounts be the same as 30: 50, as required. Similarly, Judy received 60 x. The total amount of money received is 30 x + 50 x + 60 x, so Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -25 (continued) Kai received 30 x = 30 · 18 = $540 Paulus received 50 x = 50 · 18 = $900 Judy received 60 x = 60 · 18 = $1080 Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Proportion For any rational numbers c ≠ 0, and , with a ≠ 0 and , with b, c, d ≠ 0, if and only if For any rational numbers if and only if Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Scale Drawings Ratio and proportions are used in scale drawings. The scale is the ratio of the size of the drawing to the size of the object. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.
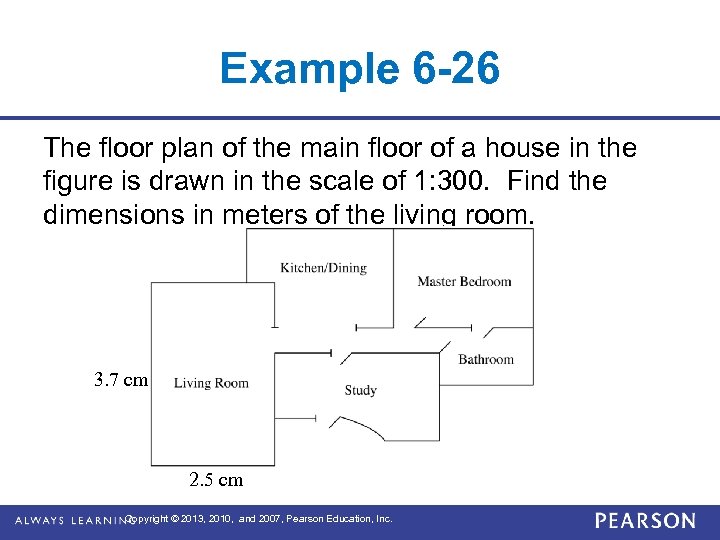
Example 6 -26 The floor plan of the main floor of a house in the figure is drawn in the scale of 1: 300. Find the dimensions in meters of the living room. 3. 7 cm 2. 5 cm Copyright © 2013, 2010, and 2007, Pearson Education, Inc.

Example 6 -26 (continued) Because the scale of 1: 300, 1 cm in the drawing represents 300 cm, or 3 m, in true size. So, 3. 7 cm represents 3. 7 · 3 = 11. 1 m and 2. 5 cm represents 2. 5 · 3 = 7. 5 m. The dimensions of the living room are 11. 1 m by 7. 5 m. Copyright © 2013, 2010, and 2007, Pearson Education, Inc.
4babeb0b9539f72e4efe88cc3049ff4e.ppt