Chapter 6 Rational Numbers and Proportional Reasoning Copyright

6 -4 Proportional Reasoning Students will be able to understand explain • Ratios and their relation to rational numbers. • Proportions and their properties. • Constant of proportionality. • Scaling. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 2

Ratios A ratio is § used to compare quantities. § usually written a: b or . § used to represent part-to-part, part-to-whole, or whole-to-part comparisons. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 3

Example There were 7 males and 12 females in the Dew Drop Inn on Monday evening. In the game room next door were 14 males and 24 females. a. Express the number of males to females at the inn as a ratio (part-to-part). b. Express the number of males to females at the game room as a ratio (part-to-part). Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 4

Example (continued) There were 7 males and 12 females in the Dew Drop Inn on Monday evening. In the game room next door were 14 males and 24 females. c. Express the number of males in the game room to the number of people in the game room as a ratio (part-to-whole). Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 5

Proportions A proportion is a statement that two given ratios are equal. If a, b, c, and d are all real numbers, and b ≠ 0 and d ≠ 0, then the proportion is true if, and only, if ad = bc. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 6

Proportions Allie and Bente type at the same speed. Allie started typing first. When Allie had typed 8 pages, Bente had typed 4 pages. When Bente has typed 10 pages, how many has Allie typed? This is an example of an additive relationship. Students should reason that since the two people type at the same speed, when Bente has typed an additional 6 pages, Allie should have also typed an additional 6 pages, so she should have typed 8 + 6, or 14, pages. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 7

Proportions Carl can type 8 pages for every 4 pages that Dan can type. If Dan has typed 12 pages, how many pages has Carl typed? This is an example of a multiplicative relationship. Since Carl types twice as fast as Dan he will type twice as many pages as Dan. Therefore, when Dan has typed 12 pages, Carl has typed 24 pages. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 8

Example If there are 3 cars for every 8 students at a high school,

Definition Constant of Proportionality If the variables x and y are related by the equality y = kx, then y is proportional to x, and k is the constant of proportionality between y and x. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 10

Definition A central idea in proportional reasoning is that a relationship between two quantities is such that the ratio of one quantity to the other remains unchanged as the numerical values of both quantities change. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 11

Scaling Strategy Use the scaling strategy to determine which is the better buy — 12 tickets for $15 or 20 tickets for $23? The scaling strategy for solving the problem would involve finding the cost for a common number of tickets, the LCM(12, 20) = 60 Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 12

Scaling Strategy In the first plan, since 12 tickets cost $15, then 60 tickets cost $75. In the second plan, since 20 tickets cost $23, then 60 tickets cost $69. The second plan is the better buy. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 13

Unit-Rate Strategy Use the unit-rate strategy to determine which is the better buy — 12 tickets for $15 or 20 tickets for $23? The unit-rate strategy for solving this problem involves finding the cost of one ticket under each plan and then comparing the unit cost. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 14

Unit-Rate Strategy In the first plan, since 12 tickets cost $15, then 1 ticket costs $1. 25. In the second plan, since 20 tickets cost $23, then 1 ticket costs $1. 15. The second plan is the better buy. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 15

Example Kai, Paulus, and Judy made $2520 for painting a house. Kai worked 30 hr, Paulus worked 50 hr, and Judy worked 60 hr. They divided the money in proportion to the number of hours worked. If they all earn the same rate of pay, how much did each earn? Let x be the unit rate or the rate of pay per hour. Then, 30 x denotes the amount of money that Kai received. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 16

Example (continued) Paulus received 50 x because then, and only then, will the ratios of the amounts be the same as 30: 50, as required. Similarly, Judy received 60 x. The total amount of money received is 30 x + 50 x + 60 x, so Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 17

Example (continued) Kai received 30 x = 30 · 18 = $540 Paulus received

Proportion For any rational numbers c ≠ 0, and , with a ≠ 0

Scale Drawings Ratio and proportions are used in scale drawings. The scale is the ratio of the size of the drawing to the size of the object. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 20

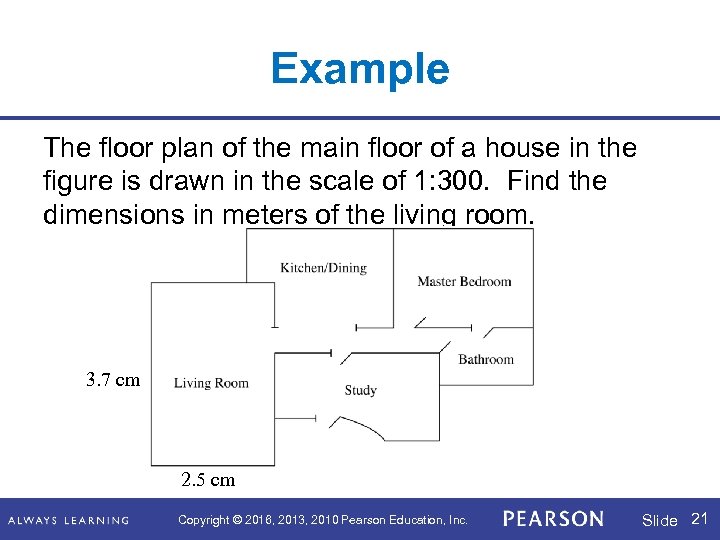
Example The floor plan of the main floor of a house in the figure is drawn in the scale of 1: 300. Find the dimensions in meters of the living room. 3. 7 cm 2. 5 cm Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 21

Example (continued) Because the scale of 1: 300, 1 cm in the drawing represents 300 cm, or 3 m, in true size. So, 3. 7 cm represents 3. 7 · 3 = 11. 1 m and 2. 5 cm represents 2. 5 · 3 = 7. 5 m. The dimensions of the living room are 11. 1 m by 7. 5 m. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 22