Chapter 6 Interest Rate Parity 熊家财 江西财经大学会计学院 xiongjc-p 163

Chapter 6: Interest Rate Parity 熊家财 江西财经大学会计学院 [email protected] com 1

Chapter 6: Interest Rate Parity 6. 1 Theory of Covered Interest Rate Parity 6. 2 Covered Interest Rate Parity in Practice 6. 3 Problems Related to Testing Interest Rate Parity 6. 4 Hedging Transaction Risk in the Money Market 6. 5 The Term Structure of Forward Premiums and Discounts 2

Ex 6. 1 Kim’s choice n Kim Deal, a portfolio manager for UBS, a Euro bank, is considering two alternative investment of € 10 million - invest in euro deposits for 1 year - invest in yen deposits for 1 year Suppose Kim has the following data: EUR interest rate 3. 5200% per annum(p. a) JPY interest rate 0. 5938% p. a Spot exchange rate ¥ 146. 0300/ € 1 -year forward exchange rate ¥ 141. 9021/ € 3

Ex 6. 1 Kim’s choice n n Choice 1: Invest in euro deposit for 1 year, after 1 year she will have € 10 000 ×（1+3. 5200%）= € 10 352 000 Choice 2: Invest in yen deposit for 1 year: - convert euro € 10 million to JPY: € 10 000 × (¥ 146. 0300/ €)=¥ 1 460 300 000 - invest her yen at 0. 5938% for 1 year: ¥ 1 460 300 000 × (1+ 0. 5938% )=¥ 1 468 971 261 - convert yen to euro at ¥ 146. 0300/ € ¥ 1 468 971 261 / (¥ 146. 0300/ €)= € 10 325 005 4

Ex 6. 2 Kevin’s choice n Suppose Kevin has $10 million to invest, and he has the following data: USD interest rate 8. 0% per annum(p. a) GBP interest rate 12. 0 % p. a Spot exchange rate $ 1. 6/ £ 1 -year forward exchange rate $ 1. 53/ £ 5

Ex 6. 2 Kevin’s choice n Choice 1: Invest in dollar deposit for 1 year, after 1 year she will have $ 10 000 ×（1+8. 0%）= € 10 800 000 n Choice 2: Invest in GBP deposit for 1 year: - convert $10 million to GBP: € 10 000 ÷ ($ 1. 6/ £)=£ 6 250 000 - invest her GBP at 0. 5938% for 1 year: £ 6 250 000 × (1+12% )= £ 7 000 - convert GBP to dollar at $ 1. 53/ £ £ 7 000 × $ 1. 53/ £=$ 10 710 000 6

Ex 6. 2 Kevin’s choice –Arbitrage borrow pound and invest in dollar n n Kevin borrow £ 1 000 at 12%, in 1 year he will owe £ 1 000 * 1. 12= £ 1 120 000 Invest in dollar - convert pound in to dollar: £ 1 000 × $ 1. 6/ £ = $ 1 600 000 - invest dollar at 8% for 1 year: $ 1 600 000 × 1. 08 = $ 1 728 000 - sell the dollar by engaging in a forward contract $ 1 728 000 ÷ ($1. 53/ £)= £ 1 129 411. 76 7

Ex 6. 2 Kevin’s choice –Arbitrage borrow pound and invest in dollar n n Borrow pound – raise the pound interest rate 12% ↑ Convert pound into dollar--- depreciate dollar-pound exchange rate $ 1. 6/ £ ↓ invest in dollar -- lower the dollar interest 8% ↓ forward purchase of pounds would raise the dollar – pound forward exchange rate $ 1. 53/ £ ↑ £ 1 000 * (1+12%) < £ 1 000 × $ 1. 6/ £ × (1+8%) ÷ ($1. 53/ £) 8

6. 1 The Theory of Covered Interest Rate Parity: Overview • The Intuition Behind Interest Rate Parity • Two Ways to Buy a Currency Forward • Why There Must Be Interest Rate Parity • Deriving Interest Rate Parity 9

6. 1 Theory of Covered Interest Rate Parity • The Intuition Behind Interest Rate Parity • Two Ways to Buy a Currency Forward • Why There Must Be Interest Rate Parity • Deriving Interest Rate Parity 10

6. 1 Theory of Covered Interest Rate Parity • Two Ways to Buy a Currency Forward • Buy a forward contract 11

6. 1 Theory of Covered Interest Rate Parity • Why There Must Be Interest Rate Parity • Covered interest rate arbitrage 12

6. 1 Theory of Covered Interest Rate Parity • Deriving Interest Rate Parity • A general expression for interest rate parity • Interest rate parity and forward premiums and discounts 13

A general expression for interest rate parity Notation: i= domestic currency interest rate for 1 period i* = foreign currency interest rate for 1 period S= the spot exchange rate (Domestic currency/ foreign currency) F= the one-period forward exchange rate (Domestic currency/ foreign currency) 14

A general expression for interest rate parity Consider an investor who has one unit of domestic currency and is considering two alternative investment - invest in domestic currency - invest in foreign currency 15

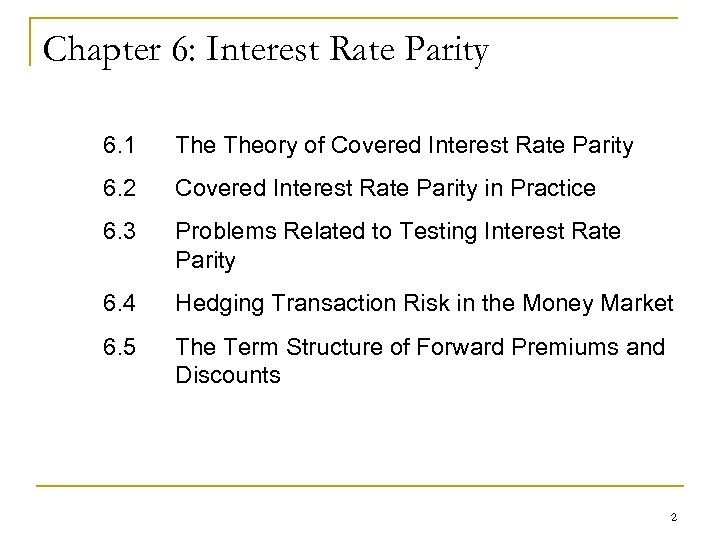
A general expression for interest rate parity Alternative 1: invest 1 unit in domestic currency, get [1+i] Alternative 2: invest 1 unit in foreign currency - convert one unit domestic into foreign currency: 1/S - invest in foreign currency: get [1/S] * [1+i*] - convert foreign into domestic: get [1/S] * [1+i*] * [F] No arbitrage: [1+i] = [1/S] * [1+i*] * [F] 16

Interest rate parity and forward premiums and discounts (1) [1+i] = [1/S] * [1+i*] * [F] 17

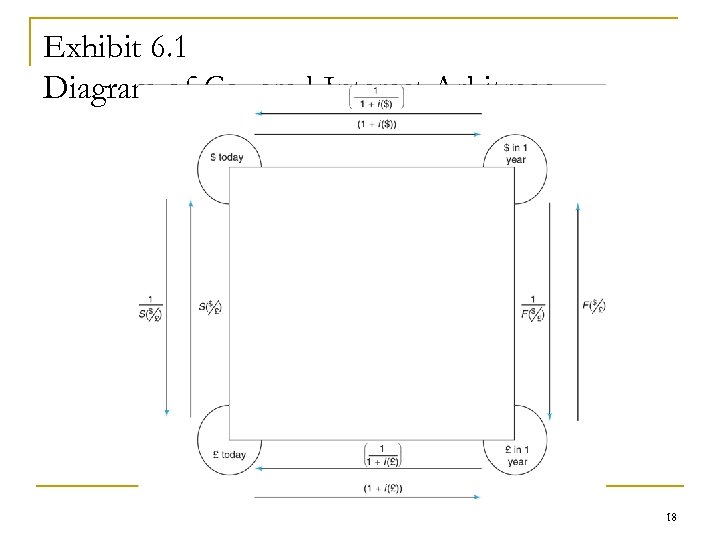
Exhibit 6. 1 Diagram of Covered Interest Arbitrage 18

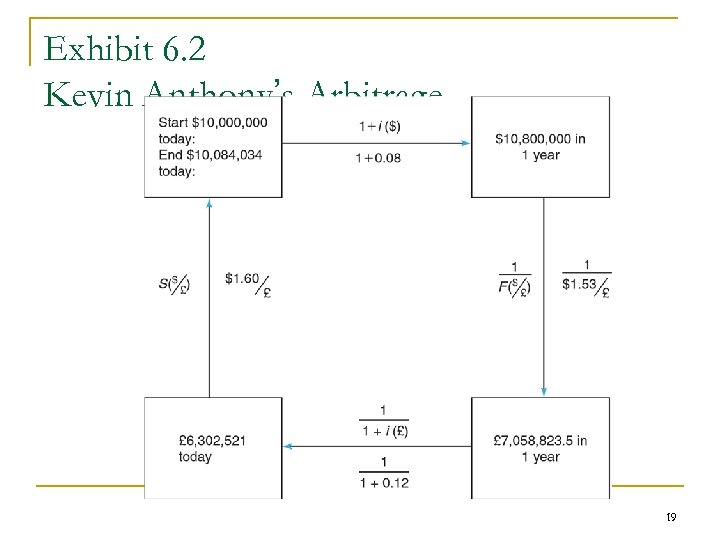
Exhibit 6. 2 Kevin Anthony’s Arbitrage 19

6. 2 Covered Interest Rate Parity in Practice • The External Currency Market • Transaction costs in the external currency market • How the external currency market affects other capital markets • London interbank offer rate (LIBOR) 20

Exhibit 6. 3 Interest Rates in the External Currency Market 21

6. 2 Covered Interest Rate Parity in Practice n Covered Interest Arbitrage with Transaction Costs q An empirical test 22

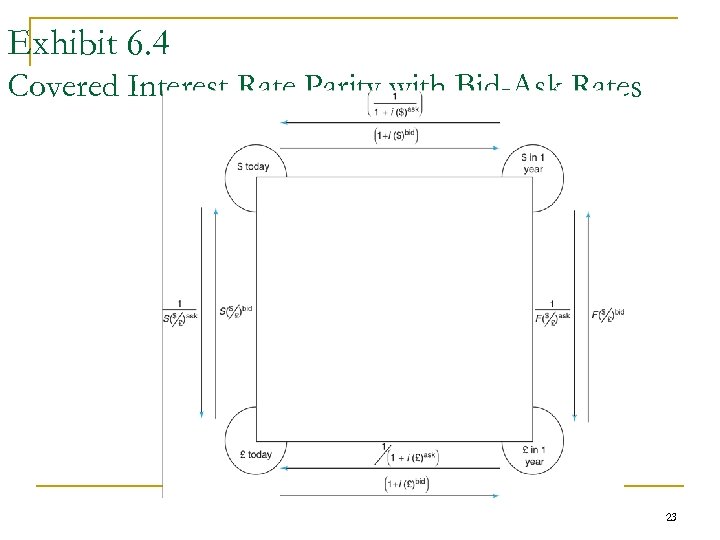
Exhibit 6. 4 Covered Interest Rate Parity with Bid-Ask Rates 23

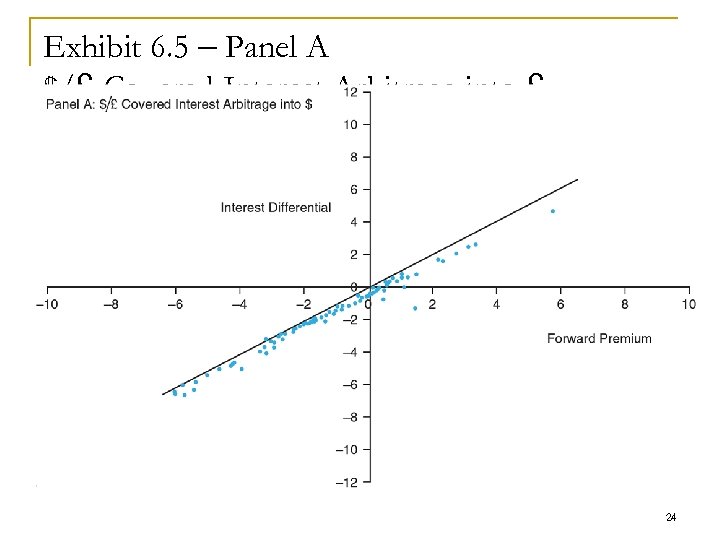
Exhibit 6. 5 – Panel A $/£ Covered Interest Arbitrage into £ 24

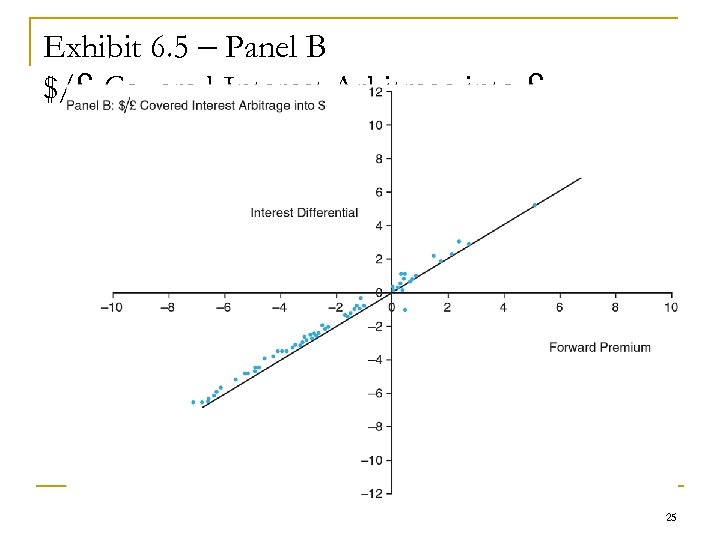
Exhibit 6. 5 – Panel B $/£ Covered Interest Arbitrage into £ 25

6. 3 Problems Related to Testing Interest Rate Parity n n Default Risks Exchange Controls Political Risk The Thrilla in Manila 26

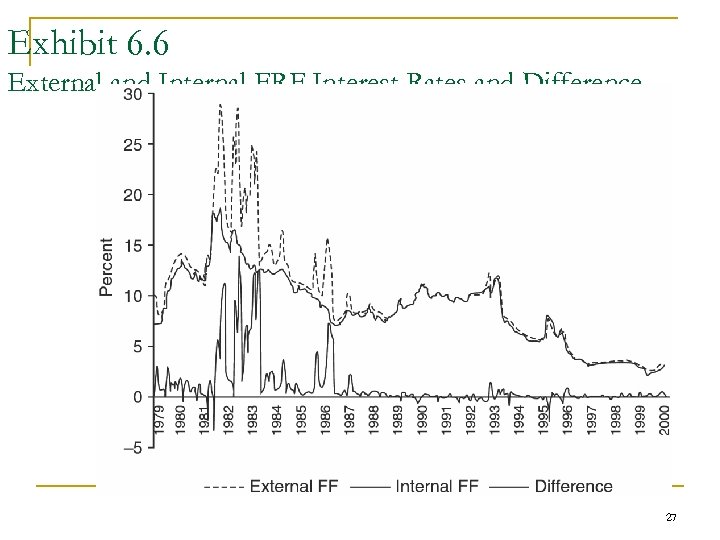
Exhibit 6. 6 External and Internal FRF Interest Rates and Difference 27

6. 4 Hedging Transaction Risk in the Money Market Hedging Transaction Risk - Money Market: Overview • Introduction • Hedging a Foreign Currency Liability • Hedging a Foreign Currency Receivable 28

6. 4 Hedging Transaction Risk in the Money Market • Introduction • Synthetic forward • Money market hedge 29

6. 4 Hedging Transaction Risk in the Money Market • Hedging a Foreign Currency Liability EX 6. 3 Zachy has just contract to import Wine from France. You has to pay € 4 million in 90 days. You have the following data: spot exchange rate $ 1. 10/ € 90 -days forward exchange rate $ 1. 08/ € 90 -days dollar interest rate: 6. 00% p. a. 90 -days euro interest rate 13. 519% p. a 30

Hedging a Foreign Currency Liability n Eliminate the risk by buying euro forward. -- The dollar paid in 90 days is equal to: € 4 000 * $ 1. 08/ € = $ 4 320 000 -- the present value of these dollar: $ 4 320 000 ÷[1+ 6%*(1/4)]= $ 4 256 157. 64 31

Hedging a Foreign Currency Liability n n hedge the risk in the money market Acquire € 4 million euro asset in 90 days -- The PV of € 4 million at 13. 519% p. a is € 4 000 ÷ [1+13. 519%*(1/4)] =€ 3 869 229. 71 -- the dollar cost : € 3 869 229. 71 * $ 1. 10/ € = $ 4 256 152. 68 32

6. 4 Hedging Transaction Risk in the Money Market • Hedging a Foreign Currency Receivable Ex 6. 4 Sland have agreed to ship sweater to Japan, and will receive ¥ 500 000 in 30 days. You have the following data: spot exchange rate 30 -days forward exchange rate 30 -days pound interest rate: 30 -days yen interest rate ¥ 179. 5 / £ ¥ 180 / £ 2. 70% p. a. 6. 01% p. a 33

Hedging a Foreign Currency Receivable n Eliminate the risk by selling yen forward. -- The pound receive in 30 days is equal to: ¥ 500 000 / (¥ 180 / £ )= £ 2 777 778 n hedge the risk in the money market Acquire ¥ 50 million yen liability in 30 days -- The PV of ¥ 50 million yen at 6. 05% p. a is n ¥ 50 000 million ÷ [1+6. 05%*(1/4)] = ¥ 497 508 313 -- sell yen for pound : ¥ 497 508 313 ÷ (¥ 179. 5 / £)= ¥ 179. 5 / £ 34

Hedging a Foreign Currency Liability n n hedge the risk in the money market Acquire ¥ 50 million yen liability in 30 days -- The PV of ¥ 50 million yen at 6. 05% p. a is ¥ 50 000 million ÷ [1+6. 05%*(1/4)] = ¥ 497 508 313 -- sell yen for pound : ¥ 497 508 313 ÷ (¥ 179. 5 / £)=£ 2 771 634 -- invest pound at 2. 70% £ 2 771 634 *[1+2. 7%*(30/365)]= £ 2777 785 35

6. 5 The Term Structure of Forward Premiums and Discounts n The Term Structure of Interest Rates q q Spot Interest Rates A Review of Bond Pricing Yields to Maturity Deriving Long-Term Spot Interest Rates 36

6. 5 The Term Structure of Forward Premiums and Discounts n Long-Term Forward Rates and Premiums 37

Problem 1. Assume that you are an importer of grain into Japan from the United States. You have agreed to make a payment in dollars, and you are scheduled to pay $377, 287 in 90 days after you receive your grain. You face the following exchange rates and interest rates: Spot exchange rate: 90 -day forward exchange rate: 90 -day dollar interest rate: ¥ 106. 35/$ ¥ 106. 02/$ 3. 25% p. a. 90 -day yen interest 1. 9375% rate: p. a. Describe the nature and extent of your transaction foreign exchange risk. b. Explain two ways to hedge the risk. c. Which of the alternatives in part b is superior?

n n A. Any weakening of the yen versus the dollar will increase the yen cost of your grain. The possible loss is unbounded. B. Choice 1: buying dollars forward at ¥ 106. 02/$ Choice 2: determine the present value of the dollars that you owe and buy that amount of dollars today in the spot market.

C : The cost of two choices: (1) buying dollars forward at ¥ 106. 02/$ $377, 287 × ¥ 106. 02/$ = ¥ 39, 999, 967. 74 in 90 days. (2) The present value of $377, 287 at 3. 25% $377, 287 / [1+(3. 25/100) (90/360) ] = $374, 246. 25 Purchasing this amount of dollars in the spot market costs ¥ 106. 35/$ × $374, 246. 25 = ¥ 39, 801, 088. 69 the future value of this Yen is ¥ 39, 801, 088. 69 * [1+ (1. 9375/100) (90/360) ]= ¥ 39, 993, 875. 2 1

Problem 2. Assume that you are an exporter of grain from Japan to the United States. You are scheduled to receive $377, 287 in 90 days after you exporter your grain. You face the following exchange rates and interest rates: Spot exchange rate: 90 -day forward exchange rate: 90 -day dollar interest rate: ¥ 106. 35/$ ¥ 106. 02/$ 3. 25% p. a. 90 -day yen interest 1. 9375% rate: p. a. 1. a. Explain two ways to hedge the risk. 2. b. Which of the alternatives in part b is superior?

Choice 1: selling dollars forward at ¥ 106. 02/$ $377, 287 × ¥ 106. 02/$ = ¥ 39, 999, 967. 74 in 90 days. n Choice 2: a. determine the present value of the dollars that you receive and sell that amount of dollars today in the spot market. b. The present value of $377, 287 at 3. 25% $377, 287 / [1+(3. 25/100) (90/360) ] =$374, 246. 25 c. sell dollar it for Yen in the spot market ¥ 106. 35/$ $374, 246. 25 × ¥ 106. 35/$ = ¥ 39, 801, 088. 69 d. invest yen at 1. 9375% , the future value of yen is ¥ 39, 801, 088. 69 * [1+ (1. 9375/100) (90/360) ]= ¥ 39, 993, 875. 2 1 n