Chapter 6 Gas Laws The Gas Phase

Chapter 6 Gas Laws

The Gas Phase • Gases have no distinct volume or shape. • Gases expand to fill the volume of their container. • Gas particles are miscible with each other. • Evidence for gas particles being far apart : § § We can see through gases We can walk through gases Gases are compressible Gases have low densities

Kinetic Theory of a Gas • Gas particles are sizeless relative to their volume. • Gas particles are in constant random motion. • Gas particles have elastic collisions. • Gas particles do not have attractive forces with each other. • The Average kinetic energy of a gas is directly proportional to absolute temperature.

Kinetic Theory of a Gas • Sizeless particles relative to the volume means that most of a gas is empty space. § We can see through a gas § We can walk through a gas • Elastic collision means that no kinetic energy is lost on impact. • If gas particles had attractive forces then they would not be mostly empty space, and be in the solid or liquid state. • Since gas particles are in constant rapid motion, then they must possess kinetic energy

Atmospheric Composition of Earth’s Atmosphere Compound Nitrogen Oxygen %(Volume) 78. 08 20. 95 Mole Fractiona 0. 7808 0. 2095 Argon Carbon dioxide Methane Hydrogen 0. 934 0. 033 2 x 10 -4 5 x 10 -5 0. 00934 0. 00033 2 x 10 -6 5 x 10 -7 a. mole fraction = mol component/total mol in mixture.

Parameters Affecting Gases • Pressure (P) • Volume (V) • Temperature (T) • Number of Moles (n)

Pressure is equal to force/unit area (P =F/A) § On earth the force related to gravity § From physics the F=ma, where m is kg and a=9. 8 m/s 2 § The units kgm/s 2 is called a Newton (N) § Since P = F/A, then pressure unit is Kgm/s 2 m 2, or N/m 2 § Pascal is the abbreviation of N/m 2 called Pa

Pressure The atomosphere is pushing with a force of 14. 7 lbs/in 2 on every surface in this room. For example each square inch on the whiteboard has 17. 7 lbs of air pushing on each square inch, which is probably several tons. Why is the white board not pushed into the next room? ?

Pressure Units • • SI units = Newton/meter 2 = 1 Pascal (Pa) 1 standard atmosphere (atm) = 101, 325 Pa § 1 atm =760 mm Hg § 1 atm = 760 torr (torr is abbreviation of mm. Hg) § § § 1 atm = 14. 7 lbs/in 2 1 atm = 1. 013 barr Barr = 100 k. Pa

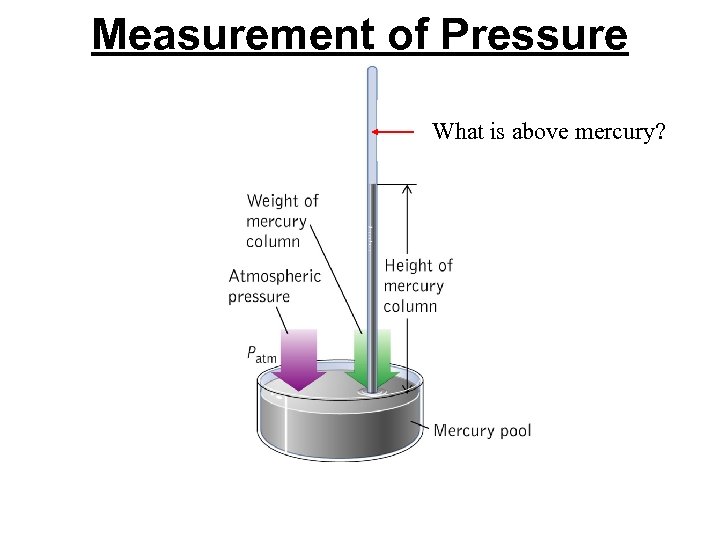Measurement of Pressure What is above mercury?

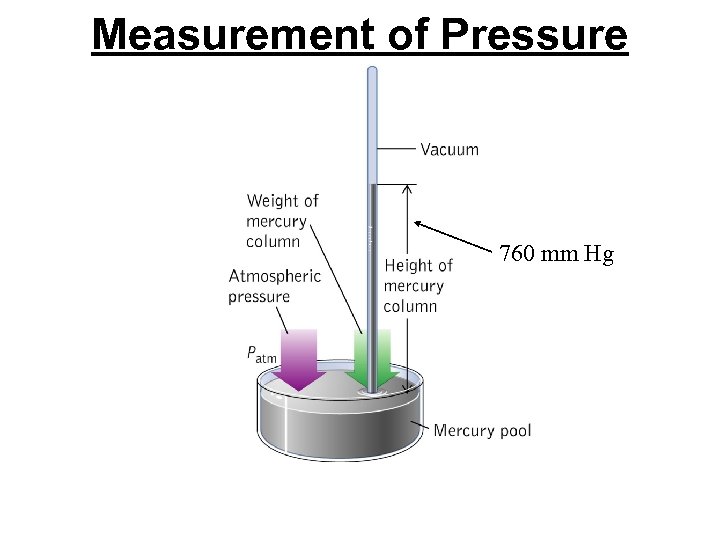Measurement of Pressure 760 mm Hg

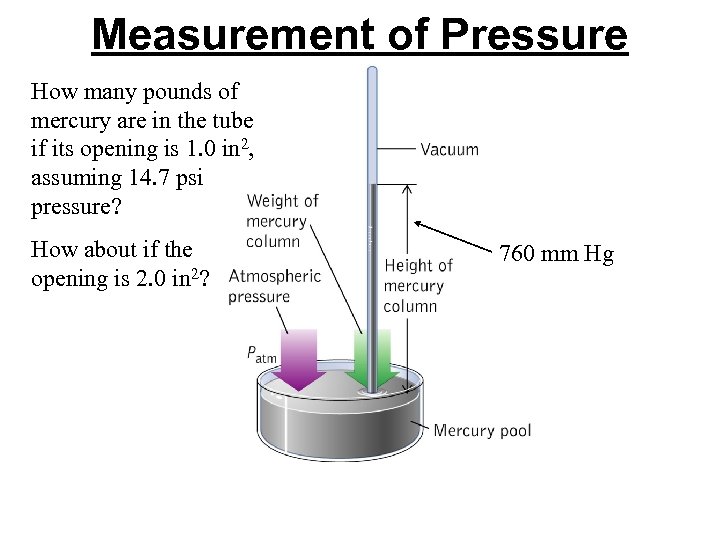Measurement of Pressure How many pounds of mercury are in the tube if its opening is 1. 0 in 2, assuming 14. 7 psi pressure? How about if the opening is 2. 0 in 2? 760 mm Hg

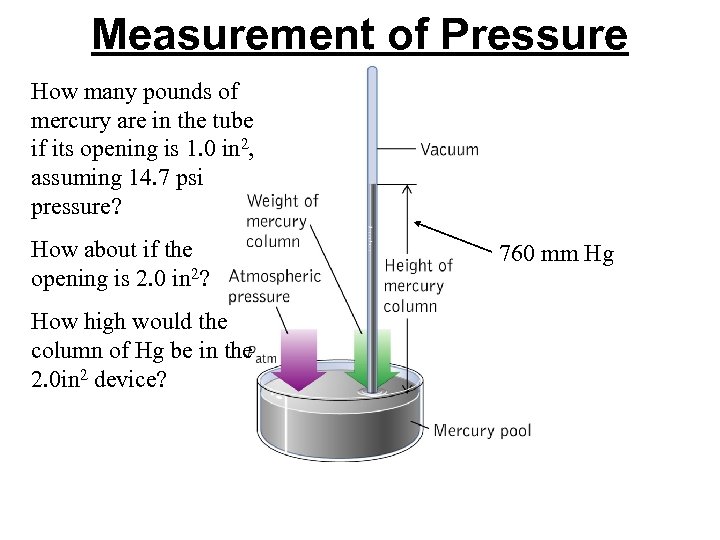Measurement of Pressure How many pounds of mercury are in the tube if its opening is 1. 0 in 2, assuming 14. 7 psi pressure? How about if the opening is 2. 0 in 2? How high would the column of Hg be in the 2. 0 in 2 device? 760 mm Hg

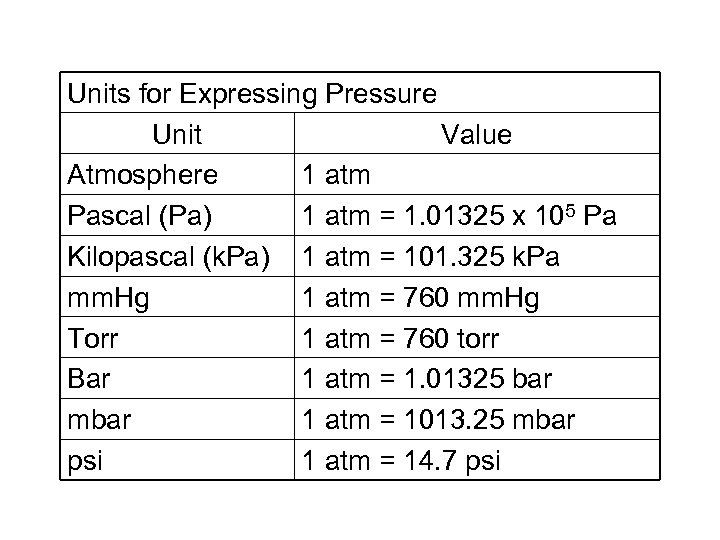Units for Expressing Pressure Unit Value Atmosphere 1 atm Pascal (Pa) 1 atm = 1. 01325 x 105 Pa Kilopascal (k. Pa) 1 atm = 101. 325 k. Pa mm. Hg 1 atm = 760 mm. Hg Torr 1 atm = 760 torr Bar 1 atm = 1. 01325 bar mbar 1 atm = 1013. 25 mbar psi 1 atm = 14. 7 psi

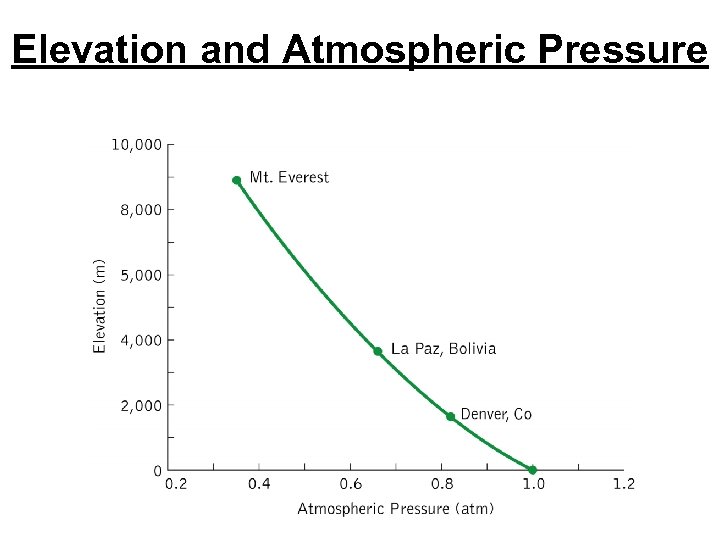Elevation and Atmospheric Pressure

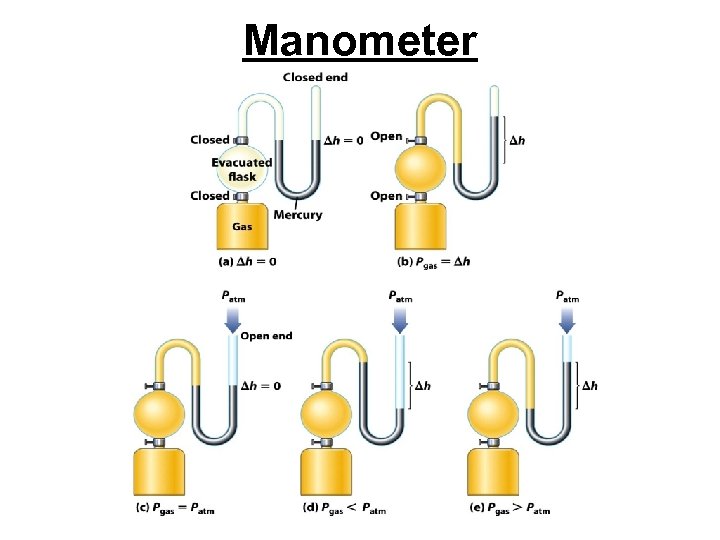Manometer

Pressure Measurement Open Tube Manometer = 15 mm Is the atmosphere or the gas in the canister pushing harder?

Pressure Measurement Open Tube Manometer Is the atmosphere or the gas in the canister pushing harder? Gas in the canister If the atmospheric pressure is = 15 mm 766 mm, then what is the pressure of the canister?

Pressure Measurement Open Tube Manometer Is the atmosphere or the gas in the canister pushing harder? Gas in the canister If the atmospheric pressure is 766 = 15 mm mm, then what is the pressure of the canister? P = 766 + 15 = 781 mm (torr) gas

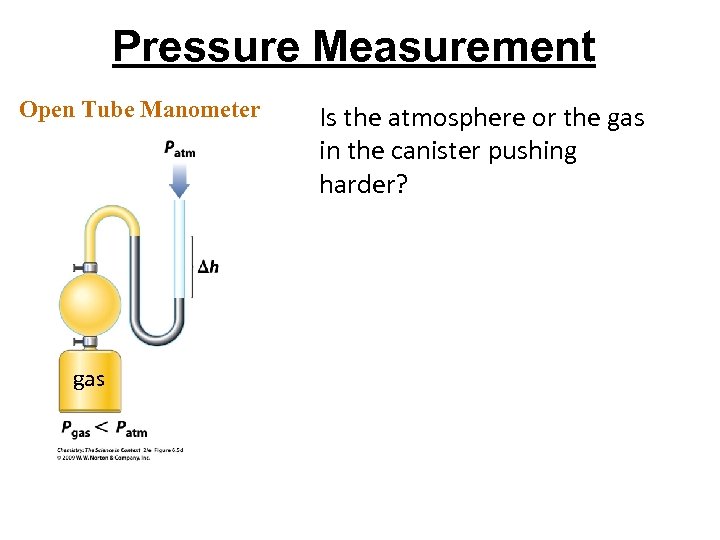Pressure Measurement Open Tube Manometer gas Is the atmosphere or the gas in the canister pushing harder?

Pressure Measurement Open Tube Manometer = 13 mm gas Is the atmosphere or the gas in the canister pushing harder? The atmosphere What is the pressure of the gas if the atmosphere is 766 mm?

Pressure Measurement Open Tube Manometer = 13 mm gas Is the atmosphere or the gas in the canister pushing harder? The atmosphere What is the pressure of the gas if the atmosphere is 766 mm? 753 mm

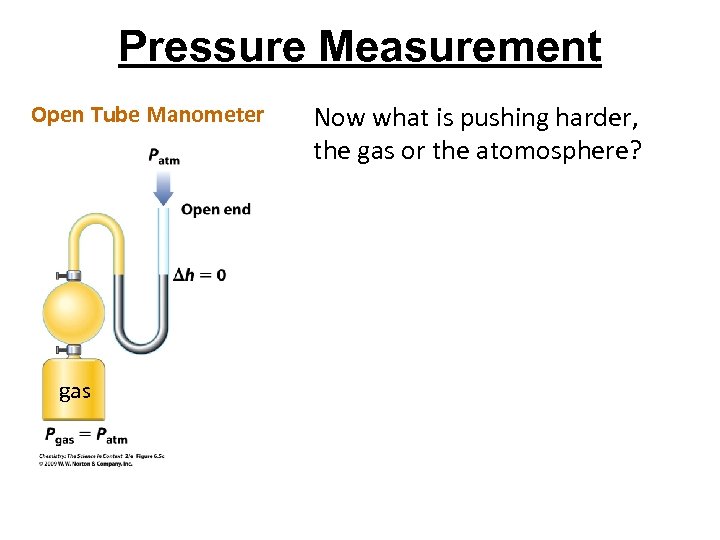Pressure Measurement Open Tube Manometer gas Now what is pushing harder, the gas or the atomosphere?

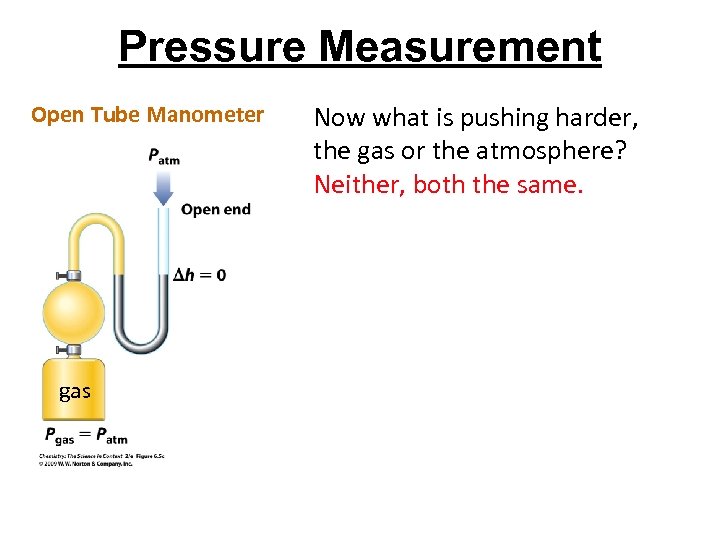Pressure Measurement Open Tube Manometer gas Now what is pushing harder, the gas or the atmosphere? Neither, both the same.

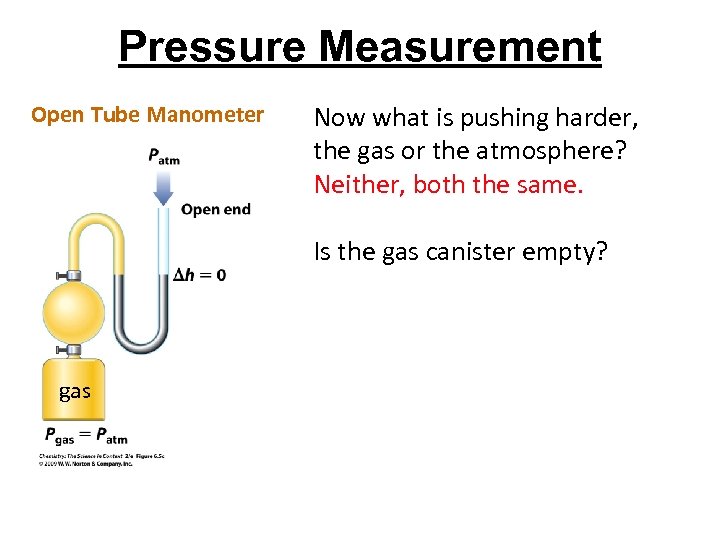Pressure Measurement Open Tube Manometer Now what is pushing harder, the gas or the atmosphere? Neither, both the same. Is the gas canister empty? gas

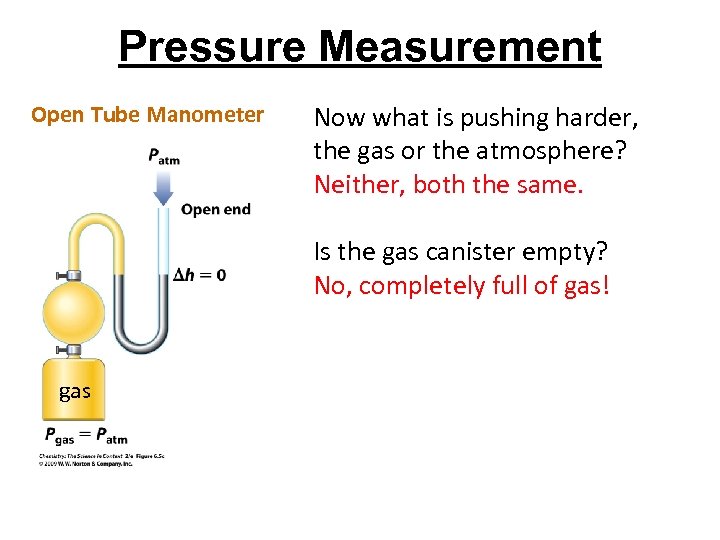Pressure Measurement Open Tube Manometer Now what is pushing harder, the gas or the atmosphere? Neither, both the same. Is the gas canister empty? No, completely full of gas! gas

Boyles Law Atm ● ● Consider a gas in a closed system containing a movable plunger. If the plunger is not moving up or down, what can be said about the pressure of the gas relative to the atmospheric pressure?

Boyles Law Atm ●● ● ● Suppose we add some red gas to the container, what would happen to the collisions of gas particles with container walls. Would they increase, decrease or stay the same?

Boyles Law Atm ●● ● ● Suppose we add some red gas to the container, what would happen to the collisions of gas particles with container walls. Would they increase, decrease or stay the same? More particles, more collisions, and more pressure. What happens to the plunger?

Boyles Law ● ● ● ● ● The number of particles remain the same, but the surface area they have to strike increases, thus the number of collisions per square inch decrease as the plunger goes up exposing more surface area causing a decrease in pressure.

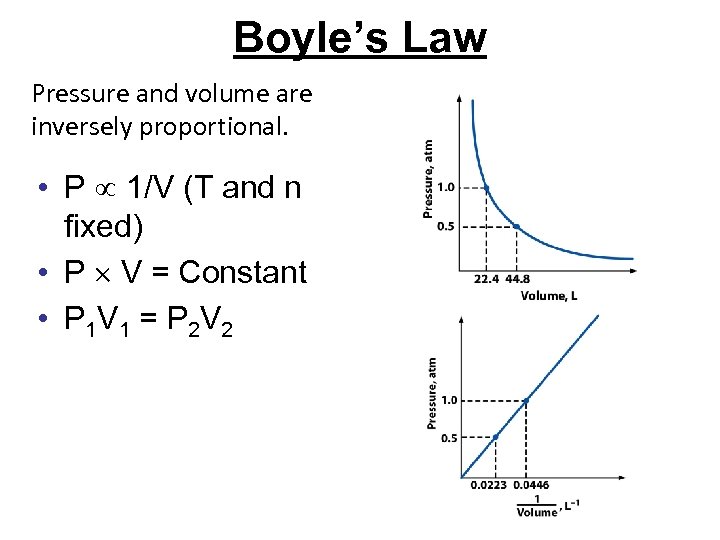Boyle’s Law Pressure and volume are inversely proportional. • P 1/V (T and n fixed) • P V = Constant • P 1 V 1 = P 2 V 2

Charles’s Law The kinetic theory of gases states that absolute temperature and kinetic energy are directly proportional. As temperature increases then particle velocity increases and the particles reach the container wall sooner, thus increasing collisions per second. Since Charles law is for constant pressure, then the volume must expand to keep a constant pressure. The mathematical statement of Charles Law is below, showing pressure and volume directly proportional. V 1 V 2 T 1 = T 2

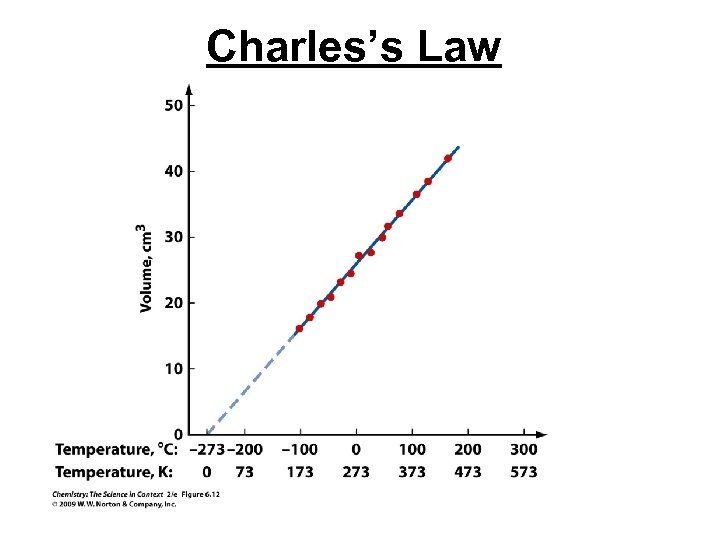Charles’s Law

Avogadro’s Law • For a gas at constant temperature and pressure, the volume is directly proportional to the number of moles of gas (at low pressures). V n V 1 = V 2 n 1 n 2

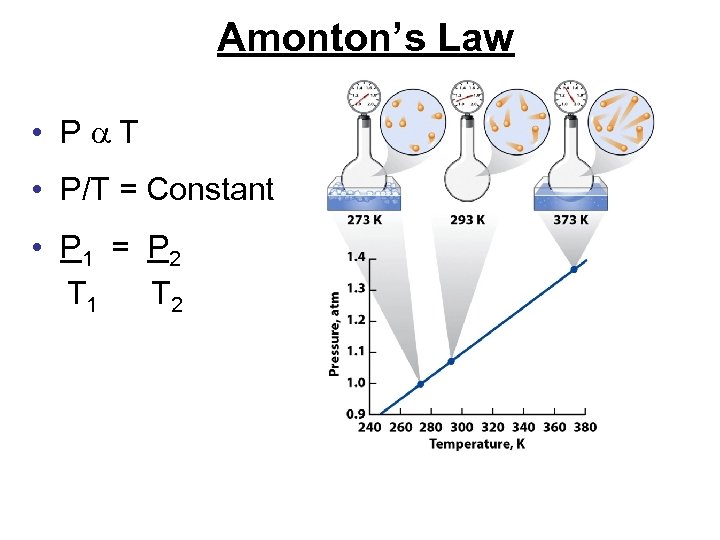Amonton’s Law • P T • P/T = Constant • P 1 = P 2 T 1 T 2

Combined Gas Law • Combining the gas laws the relationship P T(n/V) can be obtained. • If n (number of moles) is held constant, then PV/T = constant. Temperature, Kelvin, only Pressure, atm, torr, mm. Hg, Volume, L, m. L, cm 3, etc

Example A balloon is filled with hydrogen to a pressure of 1. 35 atm and has a volume of 2. 54 L. If the temperature remains constant, what will the volume be when the pressure is increased to 2. 50 atm?

Example A sample of oxygen gas is at 0. 500 atm and occupies a volume of 11. 2 L at 00 C, what volume will the gas occupy at 6. 00 atm at room temperature (250 C)?

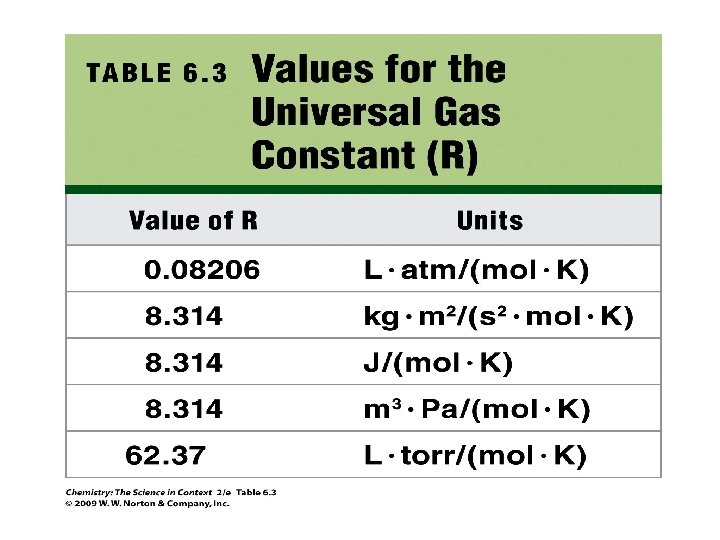
Ideal Gas Law PV = n. RT R = universal gas constant = 0. 08206 L atm K-1 mol-1 P = pressure in atm V = volume in liters n = moles T = temperature in Kelvin

Example Calculate the pressure of a 1. 2 mol sample of methane gas in a 3. 3 L container at 25°C. This problem is not a “changing condition” problem, therefore use the ideal gas law.

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass.

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass?

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm mole-K

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm 298. 15 K mole-K

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm 298. 15 K 760 torr mole-K atm

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm 298. 15 K 760 torr 1000 m. L mole-K atm L

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm 298. 15 K 760 torr 1000 m. L mole-K atm L 766 torr

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm 298. 15 K 760 torr 1000 m. L 1. 22 g mole-K atm L 766 torr 125 m. L

Practice A 1. 22 g sample of a gas is contained in a 125 m. L flask at 25⁰C and 766 torr. Find the molar mass. What are the units of molar mass? g/mole 0. 0821 L-atm 298. 15 K 760 torr 1000 m. L 1. 22 g mole-K atm L 766 torr 125 m. L = 237 g/mole

STP • “STP” means standard temperature and standard pressure § P = 1 atmosphere § T = 0 C § The molar volume of any ideal gas is 22. 42 liters at STP (for 1 mole at STP

Dalton’s Law of Partial Pressures • For a mixture of gases in a container • PTotal = P 1 + P 2 + P 3 +. . .

Mole Fraction • Mole Fraction: the ratio of the number of moles of a given component in a mixture to the total number of moles in a mixture. C 1 = n 1 n. TOTAL = n 1 + n 2 + n 3 + • • • • Mole Fraction in terms of pressure (n = PV/RT) C 1 = P 1(V/RT) + P 2(V/RT) + P 3(V/RT) + • • •

Mole Fraction C 1 = P 1 + P 2 + P 3 + • • • n 1 n. TOTAL = = P 1 PTOTAL

Mole Fraction Example At 250 C, a 1. 0 L flask contains 0. 030 moles of nitrogen, 150. 0 mg of oxygen and 4 x 1021 molecules of ammonia. A. What is the partial pressure of each gas? B. What is the total pressure in the flask? C. What is the mole fraction of each?

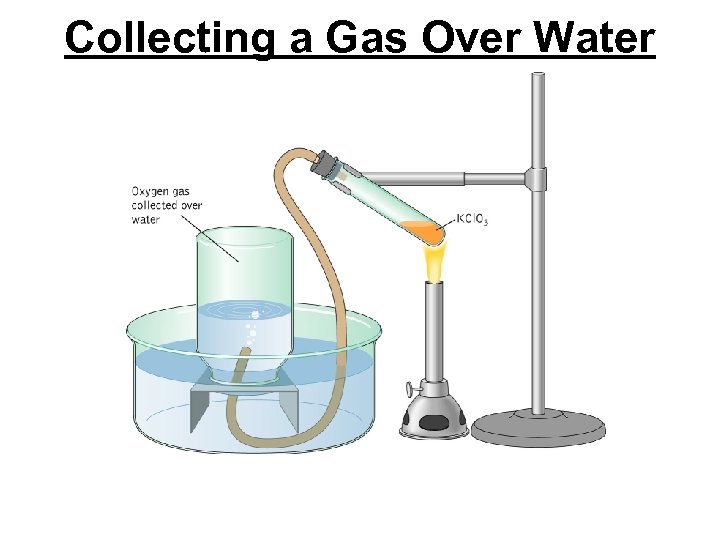Collecting a Gas Over Water

Practice A sample of KCl. O 3 is heated and decomposes to produce O 2 gas. The gas is collected by water displacement at 25°C. The total volume of the collected gas is 229 m. L at a pressure of 754 torr. How many moles of oxygen formed? Hint: The gas collected is a mixture so use Dalton’s Law to calculate the pressure of oxygen the ideal gas law to find the number of moles oxygen. PT = P + P O 2 H 2 O

Vapor Pressure of Water

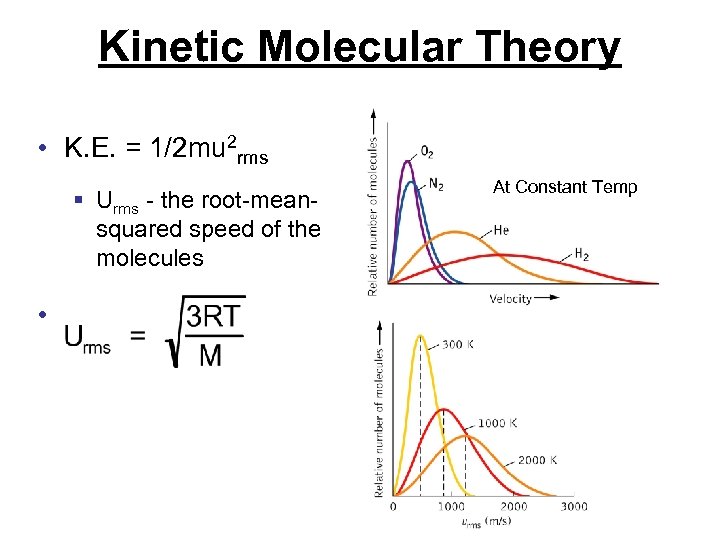Kinetic Molecular Theory • K. E. = 1/2 mu 2 rms § Urms - the root-meansquared speed of the molecules • At Constant Temp

Pressure Derivation From the kinetic molecular theory Since pressure = P/A, then the following are required to understand this concept. Translational kinetic energy of molecules Ek the greater the force Ek=1/2 mu 2. Frequency, collisions per second. The greater the frequence the greater the force Collision frequence Cf u(n/V)Impulse, the transfer of momentum when particles collide. I um

Pressure Derivation Pressure of a gas is the product of the impulse and the collision frequency P (mu)[(u)(n/V)] n/V(mu 2) Not all molecules are moving at the same speed, thus average of the squares speed must be used Why squares, because pressure is proportional to the speed squared. P n/V(muave 2) Because there are three dimensions, then P = 1/3 n/V(muave 2)

Derivation Urms Rearranging the equation P = 1/3 n/V(muave 2), gives PV = 1/3 n(muave 2) (multiply both sides by V) Since PV = n. RT, or PV=RT for one mole of gas Then 3 RT = 1/3 Na(muave 2) since a mole = Na Since (Nam)is the molar mass (M), then 3 RT = Muave 2) Solve for uave = (3 RT/M)1/2 since square root is involved uave is now renamed as urms = (3 RT/M)1/2 It should be noted that this equation, says lighter molecules of gas travel faster than heavier ones

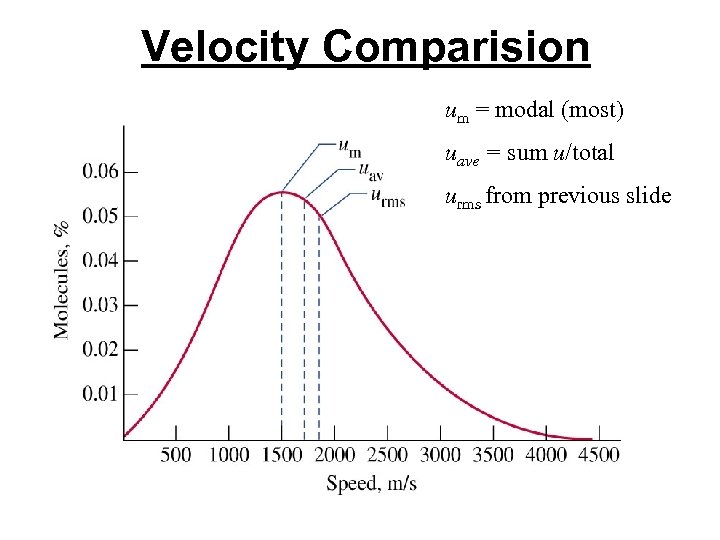Velocity Comparision um = modal (most) uave = sum u/total urms from previous slide

The mean Free Path 1. The small distance a gas travels before hitting another gas particle 10 -7 m 2. This is a small distance, but relative to gas particles it is not! 3. One effect of many collisions, in a small distance

Diffusion and Effusion Diffusion: describes the mixing of gases. The rate of diffusion is the rate of gas mixing. • Effusion: describes the escape of gas through a tiny hole into a space of lower pressure. •

Relative Rates of Effusion u 1 = (3 RT/M 1)1/2 average velocity particle #1 u 2 = (3 RT/M 2)1/2 average velocity particle #2 U 1 U 2 = (3 RT/M 2)1/2 (3 RT/M 1)1/2 = M 2 1/2 Graham’s Law M 1

Practice List the following gases, which are at the same temperature, in the order of increasing rates of diffusion. O 2, He, & NO

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature.

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass?

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass? g/mole

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass? g/mole U 1 = U 2 M 1 M 2 1/2

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass? g/mole U 1 = U 2 1 3. 25 1 8. 41 M 2 M 1 = 32. 0 1/2

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass? g/mole U 1 = U 2 1 3. 25 1 8. 41 M 2 M 1 = 32. 0 1/2 8. 41 3. 25 M 1 1/2 = 32. 0

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass? g/mole U 1 = U 2 1 3. 25 1 8. 41 M 2 M 1 = 32. 0 1/2 8. 41 3. 25 M 1 = 32. 0 1/2 2 32. 0 = M 1

Practice Calculate the molar mass of a gas if equal volumes of oxygen gas and the unknown gas take 3. 25 and 8. 41 min, respectively to effuse through a small hole under conditions of constant pressure and temperature. What are the units of molar mass? g/mole U 1 = U 2 1 3. 25 1 8. 41 M 2 M 1 = 32. 0 1/2 8. 41 3. 25 2 M 1 = 32. 0 1/2 2 32. 0 = M 1 = 214 g/mole

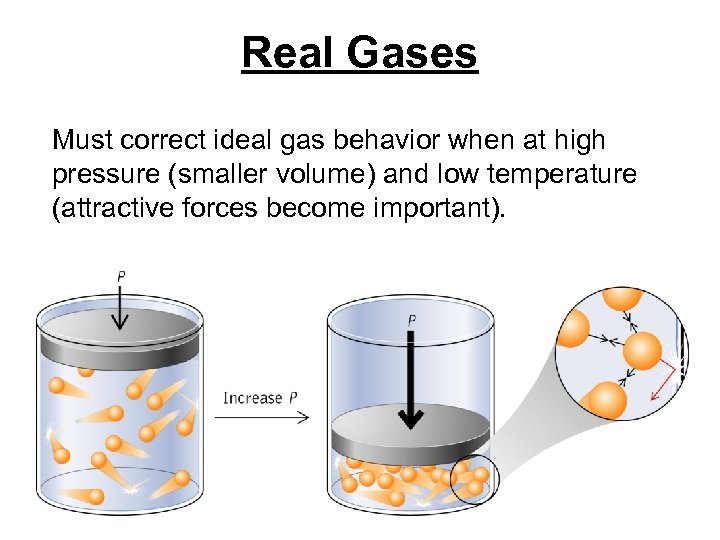Real Gases Must correct ideal gas behavior when at high pressure (smaller volume) and low temperature (attractive forces become important).

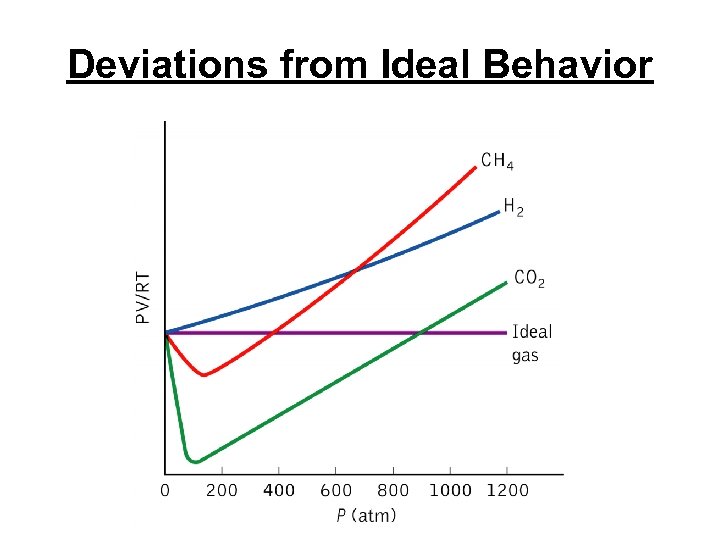Deviations from Ideal Behavior

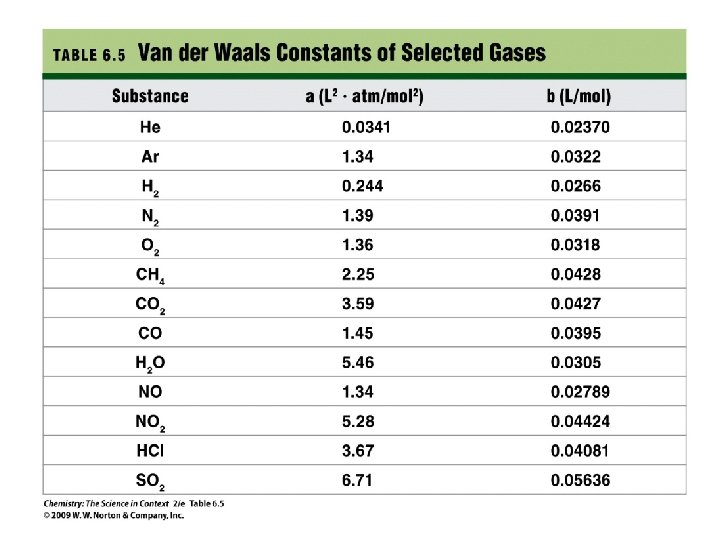
Real Gases • van der Waals Equation 2 [ P + a (n / V ) ] x (V - nb ) = n. RT obs corrected pressure Pideal corrected volume Videal

Chem. Tour: Ideal Gas Law Click to launch animation PC | Mac In this Chem. Tour, students manipulate the variables of the ideal gas law to explore the relationship between the pressure, volume, and temperature of a gas. Includes worked examples and interactive Practice Exercises.

Chem. Tour: Dalton’s Law Click to launch animation PC | Mac This Chem. Tour uses animation to explore Dalton’s law of partial pressures.

Chem. Tour: Molecular Speed Click to launch animation PC | Mac This Chem. Tour explores kinetic molecular theory. Interactive graphs illustrate the concepts of kinetic energy and root-mean- square speed.

The hydrostatic pressure on a diver’s lungs is 1 atm at the surface and increases by 1 atm for each additional 10 m below the surface. Which of the following ascents poses the gravest danger to a diver holding his or her breath? A) 10 m → 0 m B) 40 m → 20 m C) 60 m → 40 m Diving and Gas Pressure

Please consider the following arguments for each answer and vote again: A. The ascent from 10 m to 0 m is the most dangerous because the twofold decrease in pressure causes the greatest increase in lung volume. B. The ascent from 40 m to 20 m is the most dangerous because it involves a larger change in pressure. C. The ascent from 60 m to 40 m is the most dangerous because it occurs at the lowest depth. Diving and Gas Pressure

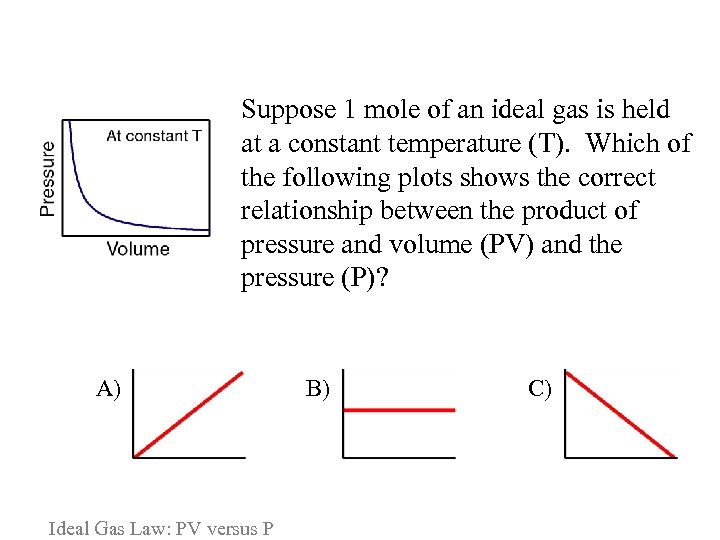
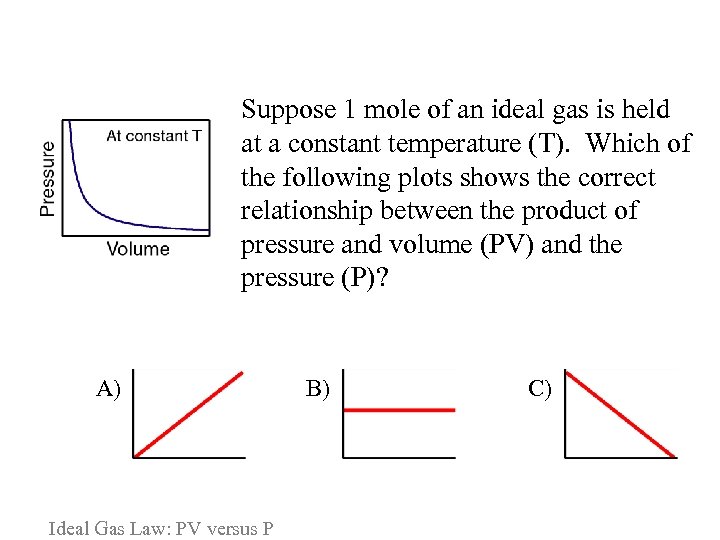Suppose 1 mole of an ideal gas is held at a constant temperature (T). Which of the following plots shows the correct relationship between the product of pressure and volume (PV) and the pressure (P)? A) Ideal Gas Law: PV versus P B) C)

Please consider the following arguments for each answer and vote again: A. As the pressure increases, the product of the pressure and the volume also should increase. B. As the pressure increases at a constant temperature, the volume should decrease so that the product PV remains constant. C. Pressure and volume are inversely proportional, so as the pressure increases, the product PV should decrease. Ideal Gas Law: PV versus P

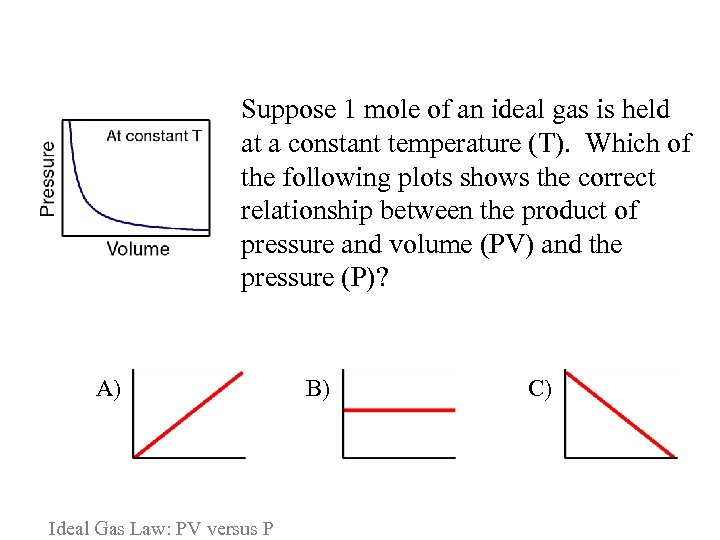
Suppose 1 mole of an ideal gas is held at a constant temperature (T). Which of the following plots shows the correct relationship between the product of pressure and volume (PV) and the pressure (P)? A) Ideal Gas Law: PV versus P B) C)

An ideal gas at 10 atm and 50 ºC is placed in a rigid cylinder fitted with a pop-off valve set to open when the pressure reaches 20 atm. How high must the temperature be raised to open the pop-off valve? A) < 100 ºC B) 100 ºC C) > 100 ºC Ideal Gas Law: Pressure Valve

Please consider the following arguments for each answer and vote again: A. Any ideal gas that is heated will expand open the valve. B. If the temperature is increased by a factor of 2, the pressure also will increase by a factor of 2 to 20 atm. C. A 50 ºC increase in the temperature will only produce a 15% increase in the pressure, which is not enough to open the valve. Ideal Gas Law: Pressure Valve

A reaction of 0. 50 atm of H 2 and 0. 50 atm of O 2 occurs in a sealed vessel at a constant temperature to form H 2 O gas. If the reaction goes to completion, what will be the final pressure? A) 0. 5 atm B) 0. 75 atm C) 1. 0 atm Pressure of Water Vapor Product

Please consider the following arguments for each answer and vote again: A. Because hydrogen is the limiting reactant, only 0. 5 atm of H 2 O will be formed. So the final pressure will be 0. 5 atm. B. Although all 0. 5 atm of H 2 will be converted into 0. 5 atm of H 2 O, only 0. 25 atm of O 2 will be consumed. Therefore, the final pressure will be 0. 75 atm. C. Because the total number of moles must be conserved, the total pressure also must be conserved. So the total pressure will remain at 1. 0 atm. Pressure of Water Vapor Product

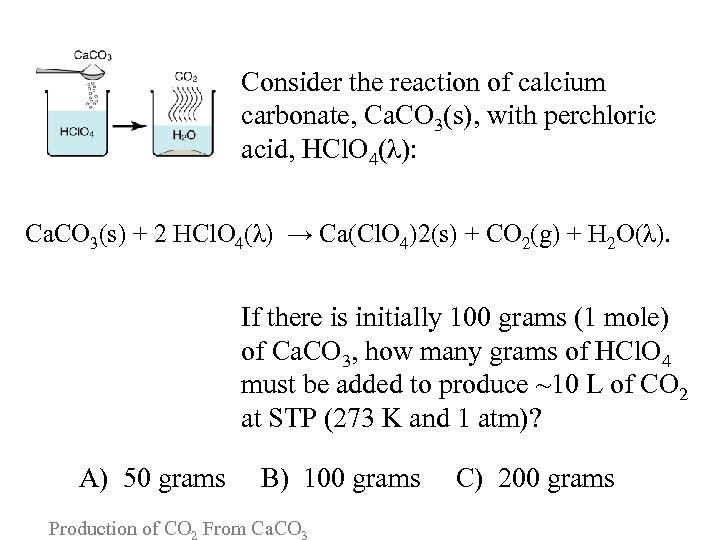Consider the reaction of calcium carbonate, Ca. CO 3(s), with perchloric acid, HCl. O 4(λ): Ca. CO 3(s) + 2 HCl. O 4(λ) → Ca(Cl. O 4)2(s) + CO 2(g) + H 2 O(λ). If there is initially 100 grams (1 mole) of Ca. CO 3, how many grams of HCl. O 4 must be added to produce ~10 L of CO 2 at STP (273 K and 1 atm)? A) 50 grams B) 100 grams C) 200 grams Production of CO From Ca. CO

Please consider the following arguments for each answer and vote again: A. 100 grams (1 mole) of Ca. CO 3 is capable of producing ~20 L (~1 mole) of CO 2, so only 50 grams (0. 5 mole) of HCl. O 4 should be added. B. 100 grams of HCl. O 4 will react completely with 50 grams of Ca. CO 3, producing ~10 L of CO 2 at STP. C. Two HCl. O 4 molecules are required for every one Ca. CO 3 molecule, so 200 grams (2 moles) of HCl. O 4 is needed. Production of CO From Ca. CO

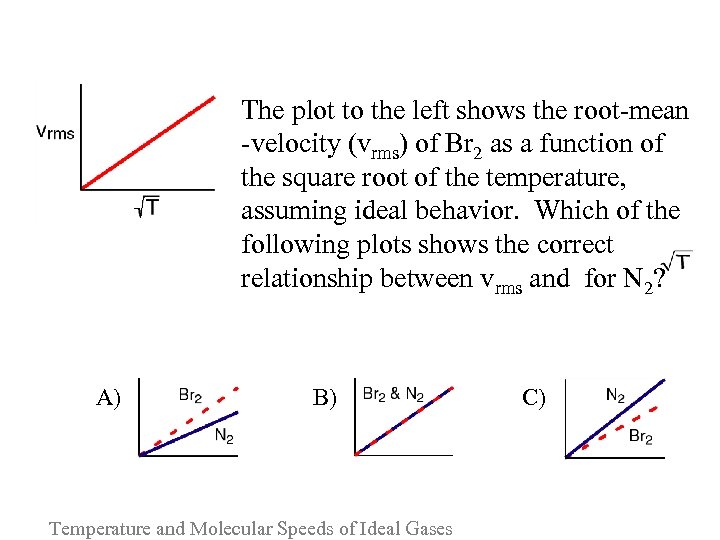The plot to the left shows the root-mean -velocity (vrms) of Br 2 as a function of the square root of the temperature, assuming ideal behavior. Which of the following plots shows the correct relationship between vrms and for N 2? A) B) Temperature and Molecular Speeds of Ideal Gases C)

Please consider the following arguments for each answer and vote again: It takes less energy (and hence a lower temperature) to increase the velocity of Br 2 molecules, so the slope of the Br 2 line should be steeper. Since both Br 2 and N 2 are assumed to be ideal gases, their slopes should be the same. Only when you consider nonideal behavior will the slopes diverge. N 2 is a lighter molecule than Br 2, and so at any given temperature its root-mean-square speed is always higher than that of Br 2. Temperature and Molecular Speeds of Ideal Gases

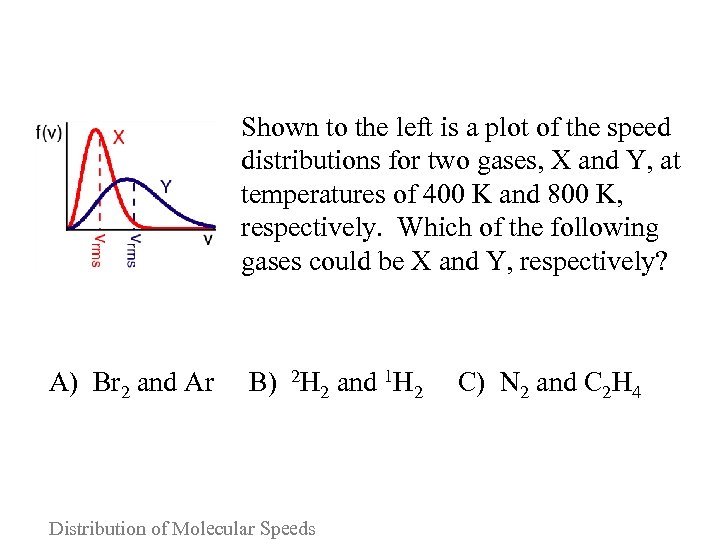Shown to the left is a plot of the speed distributions for two gases, X and Y, at temperatures of 400 K and 800 K, respectively. Which of the following gases could be X and Y, respectively? A) Br 2 and Ar B) 2 H 2 and 1 H 2 C) N 2 and C 2 H 4 Distribution of Molecular Speeds

Please consider the following arguments for each answer and vote again: A. Br 2 is four times heavier than Ar, so the root-meansquare speed (vrms) for Br 2 should be half that of argon. B. Deuterium gas (2 H 2) has twice the molecular mass of 1 H and is at a temperature half that of 2 H. As a 2 2 result, the vrms for 2 H 2 is a factor of 2 slower. C. N 2 and C 2 H 4 have the same molecular mass. However, because the temperature of C 2 H 4 is twice that of N 2, the vrms is twice as fast. Distribution of Molecular Speeds

One mole of metal, when added to 2 atm of chlorine gas (Cl 2) in a 25 -L vessel at 25 ºC, reacts to form a metal chloride, thereby decreasing the pressure to ~1 atm. Which of the following could be the unknown metal? A) Na B) Ca C) Al Reaction of Metal with Cl Gas

Please consider the following arguments for each answer and vote again: A. In a volume of 25 L at 25 ºC, 1 atm of a gas corresponds to ~1 mole. The only metal that can react in an equal molar quantity (1: 1) with chlorine is Na, which can form Na. Cl. B. At 25 ºC, 1 atm of Cl 2 in a 25 -L vessel is ~1 mole. Since 1 mole of Ca can react with 1 mole of Cl 2 to form 1 mole of Ca. Cl 2, the unknown metal must be Ca. C. Al will form Al. Cl 3, using up three-fourths of the Cl 2 and leaving an atmosphere of Cl atoms. Reaction of Metal with Cl Gas

An unopened soda can expands when left outside on a hot day. Based on this observation, what can be concluded about the dissolution of CO 2(g) in water? A) It is exothermic. B) It is endothermic. C) It is isothermal. Expansion of Soda Can upon Heating

Consider the following arguments for each answer and vote again: A. The expansion is due to the decreased solubility of CO 2(g) in water at higher temperatures, so the dissolution of CO 2(g) is exothermic. B. Energy is always required to dissolve a solute molecule in water, because to do so requires the breaking of hydrogen bonds within the water. C. The dissolution of a gas into a liquid corresponds to an isothermal compression of the gas. Expansion of Soda Can upon Heating

A single drop of water is injected into a balloon at 25 °C that contains ammonia, NH 3(g), at 1. 0 atm. What will happen to the volume of the balloon? Assume that the Henry’s constant for NH 3(g) is ~0. 02 atm/M. A) It stays the same. B) It increases. C) It decreases. Injection of H O into a Balloon of NH

Consider the following arguments for each answer and vote again: A. A single drop of water takes up very little space and can hardly affect the volume of a 1 -L balloon. B. Once added, the drop of water will immediately vaporize to mix with the NH 3(g), thus increasing the pressure and hence the volume. C. The pressure inside the balloon will drop as part of the NH 3(g) dissolves in the drop of water, thus decreasing the volume of the balloon. Injection of H O into a Balloon of NH