Chapter 5 The Time Value of Money

Chapter 5 The Time Value of Money © 2000 South-Western College Publishing

TIME VALUE OF MONEY DISCOUNTED CASH FLOW A sum of money in hand today is worth more than the same sum promised with certainty in the future. Think in terms of money in the bank The value today of a sum promised in a year is the amount you'd have to put in the bank today to have that sum in a year. Example: Future Value (FV) = $1, 000 k = 5% Then Present Value (PV) = $952. 38 because $952. 38 x. 05 = $47. 62 and $952. 38 + $47. 62 = $1, 000. 00 TM 5 -1 Slide 1 of 2

TIME VALUE OF MONEY DISCOUNTED CASH FLOW Time Lines 0 1 2 3 4 5 6 k=5 % 0 $952. 38 Outline of Approach: 1 $1, 000. 00 amount - present value amount - future value annuity - present value annuity - future value TM 5 -1 Slide 2 of 2

THE FUTURE VALUE OF AN AMOUNT FV 1 = PV + k. PV FV 1 = PV(1+k) FV 2 = FV 1 + k. FV 1 FV 2 = FV 1(1+k) Substitute for FV 1 FV 2 = PV(1+k) 2 In General, FVn = PV(1+k) n TM 5 -2 Slide 1 of 3

THE FUTURE VALUE OF AN AMOUNT Define Future Value Factor for k and n = [FVFk, n] = (1+k)n then FVn = PV [FVFk, n] = (1+k)n is tabulated for common combinations of k and n in Appendix A-1 TM 5 -2 Slide 2 of 3

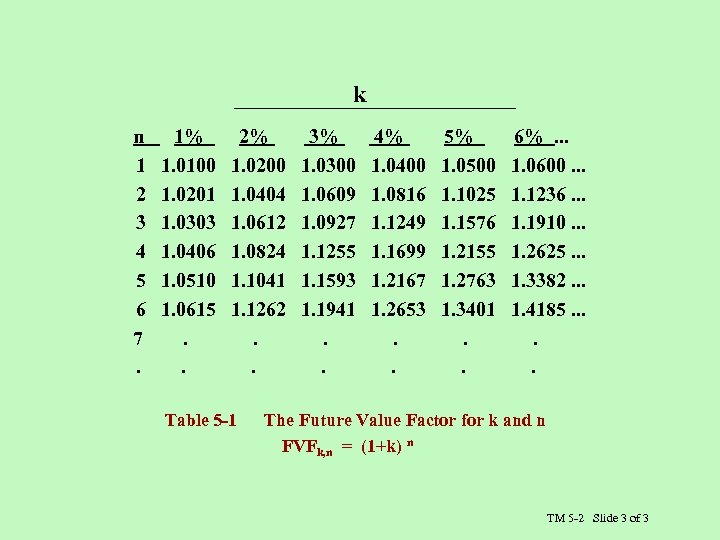k n 1 2 3 4 5 6 7. 1% 1. 0100 1. 0201 1. 0303 1. 0406 1. 0510 1. 0615. . 2% 1. 0200 1. 0404 1. 0612 1. 0824 1. 1041 1. 1262. . Table 5 -1 3% 1. 0300 1. 0609 1. 0927 1. 1255 1. 1593 1. 1941. . 4% 1. 0400 1. 0816 1. 1249 1. 1699 1. 2167 1. 2653. . 5% 1. 0500 1. 1025 1. 1576 1. 2155 1. 2763 1. 3401. . 6%. . . 1. 0600. . . 1. 1236. . . 1. 1910. . . 1. 2625. . . 1. 3382. . . 1. 4185. . . The Future Value Factor for k and n FVFk, n = (1+k) n TM 5 -2 Slide 3 of 3

Example 5 -1 How much will $850 be worth if deposited for three years at 5% interest? Solution: FVn = PV [FVFk, n] FV 3 = $850 [FVF 5, 3] Look up FVF 5, 3 = 1. 1576 FV 3 = $850 [1. 1576] = $983. 96 Problem Solving Techniques Equations all contain four variables (In this case PV, FVn, k, and n) Every problem will give three and ask for the fourth. TM 5 -3

Example 5 -2 Ed Johnson sold land to Harriet Smith for $25, 000. Terms: $15, 000 down, $5, 000 a year for two years. What was the "real" purchase price if the interest rate available to Ed is 6%? Solution: Price today is $15, 000 plus PV of two $5, 000 payments in future FVn = PV [FVFk, n] $5, 000 = PV [FVF 6, 1] $5, 000 = PV [1. 0600] PV = $4, 716. 98. and $5, 000 = PV [FVF 6, 2] $5, 000 = PV [1. 1236] PV = $4, 449. 98 $15, 000. 00 + $4, 716. 98 + $4, 449. 98 = $24, 166. 96 The terms of sale imply an equivalent discount of $833. 04 even though the real estate records indicate a price of $25, 000 TM 5 -4 Slide 1 of 2

The Opportunity Cost Rate Example 5 -2 (continued) 6% was available to the seller nothing was actually invested at that rate In a sense, seller lost income at that rate by giving the deferred payment terms. Suppose Harriet Smith borrows to pay for land at 10%. Her opportunity cost rate is 10% And the deferred payment terms are worth a discount of $1, 317. 31 to her Deferred terms are worth more to the recipient than to the donor! The opportunity cost of a resource is the amount it could earn in the next best use. TM 5 -4 Slide 2 of 2

THE PRESENT VALUE OF AN AMOUNT PVFk, n Present Value Factor for k and n (Appendix A-2) PV = FVn[PVFk, n] The Reciprocal Relation Between FVF and PVF TM 5 -5 Slide 1 of 2

More on Problem Solving Technique If unknown is k or n, can't solve equations algebraically Solve for factor and use table Example 5 -3 What interest rate will grow $850 into $983. 96 in three years? Solution: PV = FVn[PVFk, n] $850. 00 = $983. 96 [PVFk, 3] PVFk, 3 = $850. 00 / $983. 96 =. 8639 Find. 8639 in Table A-2, along the row for three years and read 5% at top TM 5 -5 Slide 2 of 2

Example 5 -4 How long does it take money invested at 14% to double? Solution: FVn = PV [FVFk, n] FVF 14, n = FVn / PV = 2. 0000 (Search for 2. 0000 in Appendix A-1, along the column for k = 14% Table value is between 5 and 6 years) TM 5 -6

ANNUITIES A stream of equal payments, made or received, separated by equal intervals of time. 0 1 2 3 $1, 000 4 $1, 000 Figure 5 -1 Ordinary Annuity 0 1 $1, 000 2 3 $1, 000 Figure 5 -2 4 $1, 000 Annuity Due TM 5 -7

THE FUTURE VALUE OF AN ANNUITY DEVELOPING A FORMULA 0 1 2 3 PMT PMT Each PMT earns interest at rate k from the time it appears on the time line until the end of the last period The future value of the annuity is the sum of all the payments and all the interest Equivalent to summing the future value of each PMT treated as an amount TM 5 -8 Slide 1 of 3

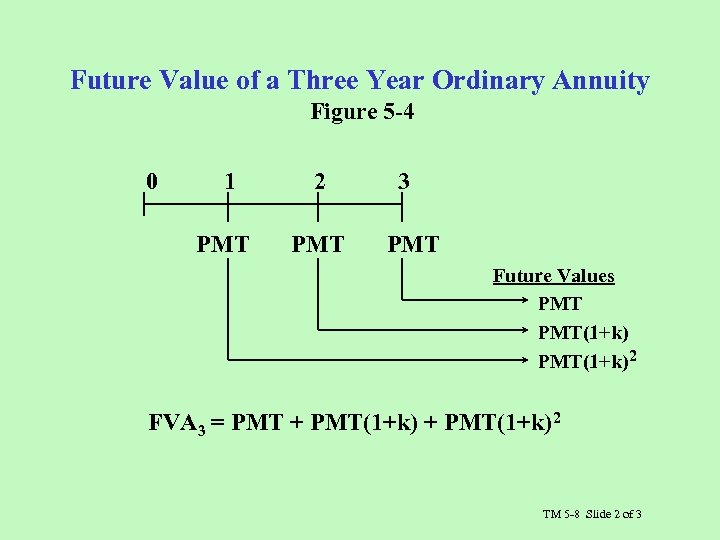Future Value of a Three Year Ordinary Annuity Figure 5 -4 0 1 PMT 2 PMT 3 PMT Future Values PMT(1+k)2 FVA 3 = PMT + PMT(1+k)2 TM 5 -8 Slide 2 of 3

Future Value of a Three Year Ordinary Annuity The Three Year Formula FVA = PMT(1+k)0 + PMT(1+k)1 + PMT(1+k)2 Generalizing the Expression FVAn = PMT (1+k)n-i The Future Value Factor for an Annuity FVAn = PMT (1 + k)n-i = FVFAk, n (Appendix A-3) FVAn = PMT [FVFAk, n] TM 5 -8 Slide 3 of 3

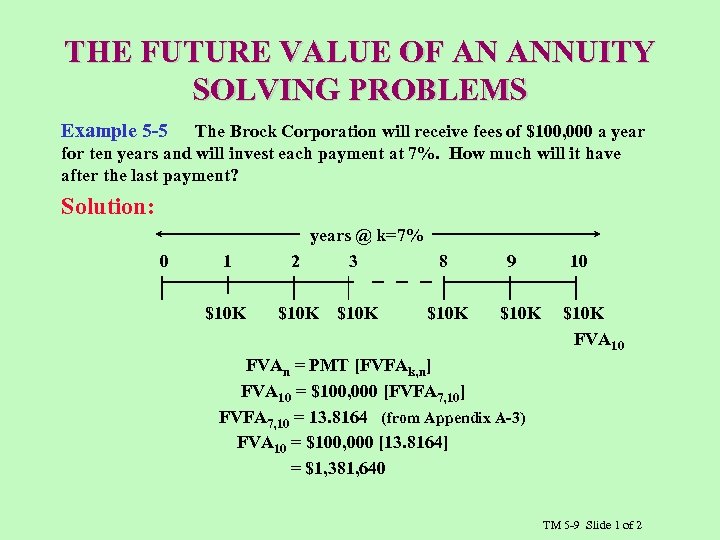THE FUTURE VALUE OF AN ANNUITY SOLVING PROBLEMS Example 5 -5 The Brock Corporation will receive fees of $100, 000 a year for ten years and will invest each payment at 7%. How much will it have after the last payment? Solution: 0 1 $10 K years @ k=7% 2 3 8 $10 K 9 $10 K 10 $10 K FVA 10 FVAn = PMT [FVFAk, n] FVA 10 = $100, 000 [FVFA 7, 10] FVFA 7, 10 = 13. 8164 (from Appendix A-3) FVA 10 = $100, 000 [13. 8164] = $1, 381, 640 TM 5 -9 Slide 1 of 2

Example 5 -6 The Sinking Fund Problem A sinking fund is a series of payments made into an account dedicated to paying off a bond's principal at maturity. Problem: How much must be deposited periodically given an interest rate and a term? Greenville Co. bonds - $15 million, 30 years, sinking fund after ten years, assume k = 6%, how much should be deposited each year? Solution: years @ k=6% 0 1 PMT 2 PMT 3 PMT 18 PMT 19 PMT 20 PMT FVA 20 = $15 M FVAn = PMT [FVFAk, n] $15, 000 = PMT [FVFA 6, 20] FVFA 6, 20 = 36. 7856 (from Appendix A-3) $15, 000 = PMT [36. 7856] PMT = $407, 768. 26 TM 5 -9 Slide 2 of 2

COMPOUND INTEREST AND NON-ANNUAL COMPOUNDING Compound Interest Earning interest on previously earned interest Bank Balance Time Figure 5 -5 The Effect of Compound Interest TM 5 -10 Slide 1 of 2

Compounding Periods Frequency with which interest is credited for calculating future interest, usually annually, semiannually, quarterly, or monthly. The shorter the period, the more interest is earned on interest Annually 12% $100 $112 Semiannually 6% 6% $100 $106 $112. 36 Quarterly 3% $100 3% $103 3% $106. 09 3% $109. 27 $112. 55 Quote the annual (nominal) rate (knom) stating the compounding period immediately afterward "12% compounded quarterly" TM 5 -10 Slide 2 of 2

The Effective Annual Rate (EAR) The rate of annually compounded interest equivalent to the nominal rate compounded more frequently Compounding Annual Semiannual Quarterly Monthly Table 5 -2 Final balance $112. 00 $112. 36 $112. 55 $112. 68 Year End Balances at Various Compounding Periods $100 Initial Deposit and knom = 12% In general: TM 5 -11 Slide 1 of 2

COMPOUNDING PERIODS AND THE TIME VALUE FORMULAS Time periods must be compounding periods and the interest rate must be the rate for a single compounding period Semiannually: k = knom / 2 Quarterly: k = knom / 4 Monthly: k = knom / 12 n = years 4 n = years 12 TM 5 -11 Slide 2 of 2

Example 5 -7 Save up to buy a $15, 000 car in 2 1/2 years. Bank pays 12% compounded monthly. How much must be deposited each month? Solution: k = knom/12 = 12%/12 = 1% n = 2. 5 yr 12 mo/yr = 30 months FVAn = PMT [FVFAk, n] $15, 000 = PMT [FVFA 1, 30] $15, 000 = PMT [34. 785] PMT = $431. 22 TM 5 -12

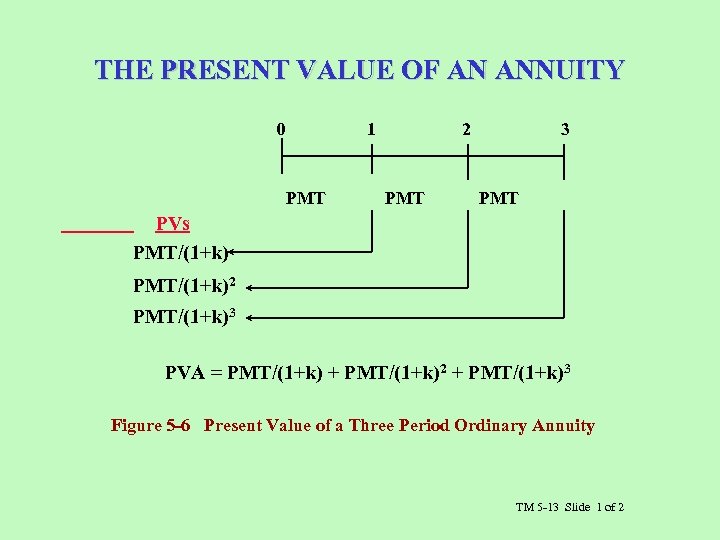THE PRESENT VALUE OF AN ANNUITY 0 1 PMT 2 PMT 3 PMT PVs PMT/(1+k)2 PMT/(1+k)3 PVA = PMT/(1+k) + PMT/(1+k)2 + PMT/(1+k)3 Figure 5 -6 Present Value of a Three Period Ordinary Annuity TM 5 -13 Slide 1 of 2

Generalizing: PVA = PMT(1+k)-1 + PMT(1+k)-2 +. . . + PMT(1+k)-n PVA = PMT [PVFAk, n] Appendix A-4 TM 5 -13 Slide 2 of 2

THE PRESENT VALUE OF AN ANNUITY SOLVING PROBLEMS Example 5 -9 The Shipson Company will receive payments of $5, 000 every six months (semiannually) for ten years on a sales contract which the bank will discount at 14% compounded semiannually. How much will Shipson receive? Solution: k = knom/2 = 14%/2 = 7% 0 n = 10 yrs 2 = 20 Half years @ k=7% 1 2 3 18 19 $5 K $5 K 20 $5 K $5 K PVA = PMT [PVFAk, n], PVA = $5, 000 [PVFA 7, 20] PVA = $5, 000 [10. 5940] PVA = $52, 970 TM 5 -14

AMORTIZED LOANS Principal is paid off gradually during loan's life Generally structured so that a constant payment is made periodically, usually monthly Each payment contains one month's interest and an amount to reduce principal Interest is charged on the month beginning loan balance As loan's principal is reduced interest charges become smaller Since monthly payments are constant successive payments contain larger proportions of principal repayment and smaller proportions of interest TM 5 -15 Slide 1 of 3

Example 5 -10 How much is the monthly payment on a $10, 000 loan to be repaid in monthly installments over four years at 18% (compounded monthly)? Solution: k = knom/12 = 18%/12 = 1. 5% n = 4 yrs 12 mo/yr = 48 months PVA = PMT [PVFAk, n] $10, 000 = PMT [PVFA 1. 5, 48] $10, 000 = PMT [34. 0426] PMT = $293. 75 TM 5 -15 Slide 2 of 3

Example 5 -11 How much can you borrow at 12% compounded monthly over three years if you can make payments of $500 per month? Solution: k = knom/12 = 12%/12 = 1% n = 3 yrs 12 mo/yr = 36 months PVA = PMT [PVFAk, n] PVA = $500 [PVFA 1, 36] PVA = $500 [30. 1075] PVA = $15, 053. 75 A loan is always a PVA problem Amount borrowed is always PVA Loan payment is always PMT TM 5 -15 Slide 3 of 3

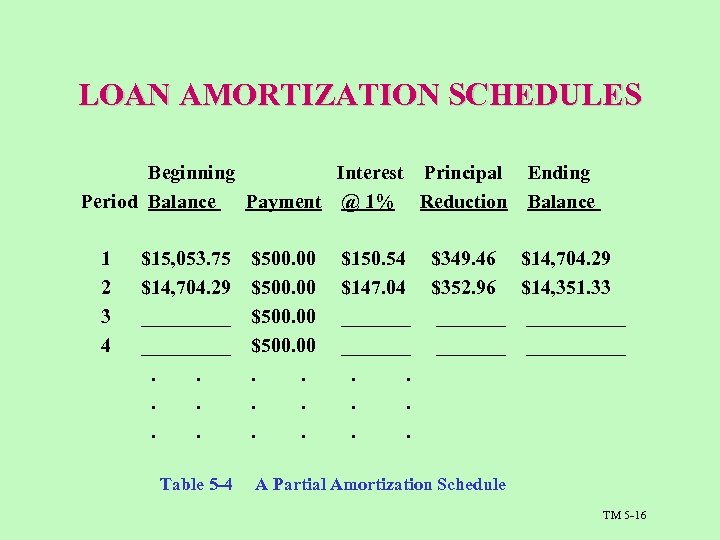LOAN AMORTIZATION SCHEDULES Beginning Interest Principal Period Balance Payment @ 1% Reduction 1 2 3 4 $15, 053. 75 $14, 704. 29 _________. . . Table 5 -4 $500. 00. . . $150. 54 $147. 04 _______. . . Ending Balance $349. 46 $14, 704. 29 $352. 96 $14, 351. 33 __________ A Partial Amortization Schedule TM 5 -16

MORTGAGE LOANS Early payments are nearly all interest Later Payments are nearly all principal Example A thirty year, $100, 000 mortgage at 12% (compounded monthly) has a monthly payment of $1, 028. 61 First month's interest is $1, 000 (1% of $100, 000) Only $28. 61 is applied to principal The first payment is 97. 2% interest Reverses in last months TM 5 -17 Slide 1 of 3

Tax Effect of Mortgage Payments Mortgage interest is tax deductible Effective first payment at 28%: Payment $1, 028. 61 Tax Savings 280. 00 Net $ 748. 61 Payoff Timing Halfway through a mortgage's life, it isn't half paid off: Present value of the second half of the payment stream The amount one could borrow making 180 payments of $1, 028. 61 PVA = PMT [PVFAk, n] = $1, 028. 61 [PVFA 1, 180] = $1, 028. 61 [83. 3217] = $85, 705. 53 TM 5 -17 Slide 2 of 3

Total Interest Paid Total payments = $1, 028. 61 360 = $370, 299. 60 Less original loan = 100, 000. 00 Total Interest = $270, 299. 60 Tax Savings @ 28% 75, 683. 89 Net Interest Cost $194, 615. 71 TM 5 -17 Slide 3 of 3

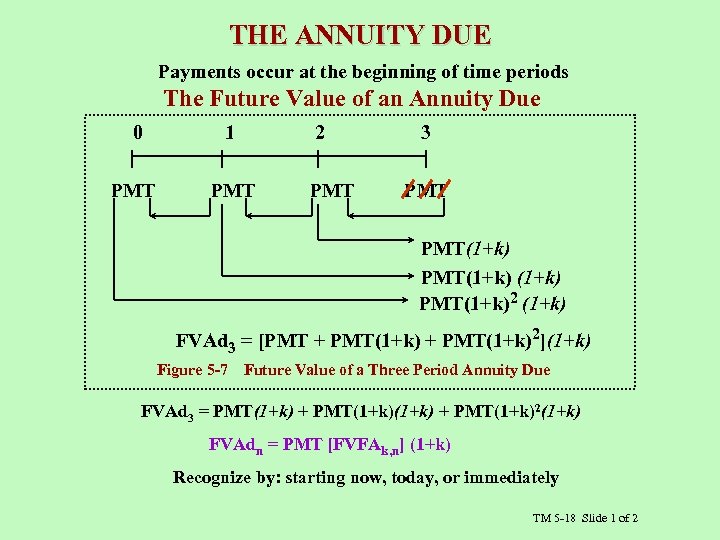THE ANNUITY DUE Payments occur at the beginning of time periods The Future Value of an Annuity Due 0 1 2 PMT PMT 3 PMT(1+k) PMT(1+k)2 (1+k) FVAd 3 = [PMT + PMT(1+k)2](1+k) Figure 5 -7 Future Value of a Three Period Annuity Due FVAd 3 = PMT(1+k) + PMT(1+k)2(1+k) FVAdn = PMT [FVFAk, n] (1+k) Recognize by: starting now, today, or immediately TM 5 -18 Slide 1 of 2

Example 5 -12 The Baxter Corporation began 10 years of quarterly $50, 000 sinking fund deposits today at 8% compounded quarterly. What will the fund be worth in 10 years? Solution: k = 8%/4 = 2% n = 10 yrs 4 qtrs/yr = 40 qtrs FVAdn = PMT [FVFAk, n] (1+k) FVAd 40 = $50, 000 [FVFA 2, 40] (1. 02) FVAd 40 = $50, 000 [60. 4020] (1. 02) = $3, 080, 502. 00 The Present Value of an Annuity Due PVAd = PMT [PVFAk, n] (1+k) TM 5 -18 Slide 2 of 2

RECOGNIZING TYPES OF ANNUITY PROBLEMS 0 1 PVA Transaction Here 2 n -1 n FVA Transaction Here A loan is always a present value of an annuity problem The annuity is the stream of loan payments The transaction is the transfer of the amount borrowed from the lender to the borrower Saving up is always a future value of an annuity problem TM 5 -19 Slide 1 of 3

PERPETUITIES A series of equal payments which occur at equal intervals and go on forever k = interest rate for the payment period Example 5 -13: Preferred Stock - Longhorn Corporation issues a security that pays $5 per quarter indefinitely. The interest rate is 8% compounded quarterly. What is the security's value? Solution: TM 5 -19 Slide 2 of 3

Example 5 -14: Capitalization of Earnings Ebertek is expected to earn $2. 5 million per year indefinitely. The interest rate is 10%. What is the company's value? Solution: TM 5 -19 Slide 3 of 3

CONTINUOUS COMPOUNDING FVn = PV (ekn) Where k = nominal rate in decimal form n = years e = 2. 71828. . . Example 5 -15: a. Future value of $5, 000 at 6 1/2% compounded continuously for 3 1/2 years b. The Equivalent Annual Rate (EAR) of 12% compounded continuously? TM 5 -20 Slide 1 of 2

Solution: a. FVn = PV (ekn) FV 3. 5 = $5, 000 (e(. 065)(3. 5)) = $5, 000 (e. 2275) = $5, 000 (1. 255457) FV 3. 5 = $6, 277. 29 b. Deposit $100 for one year: FVn = PV (ekn) FV 1 = $100 (e(. 12)(1)) = $100 (e. 12) = $100 (1. 1275) = $112. 75 Initial deposit = $100, Interest earned = $12. 75, EAR = $12. 75 / $100 = 12. 75% TM 5 -20 Slide 2 of 2

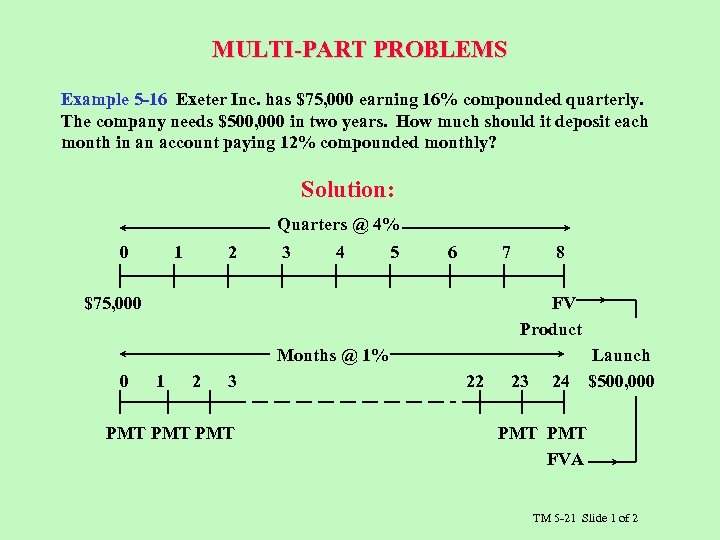MULTI-PART PROBLEMS Example 5 -16 Exeter Inc. has $75, 000 earning 16% compounded quarterly. The company needs $500, 000 in two years. How much should it deposit each month in an account paying 12% compounded monthly? Solution: Quarters @ 4% 0 1 2 3 4 5 6 7 $75, 000 8 FV Product Months @ 1% 0 1 2 3 PMT PMT 22 23 24 Launch $500, 000 PMT FVA TM 5 -21 Slide 1 of 2

First find the future value of the $75, 000 FVn = PV [FVFk, n] FV 8 = $75, 000 [FVF 4, 8] = $75, 000 [1. 3686] = $102, 645 Then the savings annuity must provide $500, 000 - $102, 645 = $397, 355 FVAn = PMT [FVFAk, n] $397, 355 = PMT [FVFA 1, 24] $397, 355 = PMT [26. 9735] PMT = $14, 731 TM 5 -21 Slide 2 of 2

Example 5 -17 The Smith family plans to buy a $200, 000 house using a traditional thirty year mortgage. Banks allow roughly 25% of income to be applied to mortgage payments. The Smiths expect their income will be $48, 000. and the mortgage interest rate will be 9% when they buy the house. They now have $10, 000 in a bank account which pays 6% compounded quarterly. How much will they have to add to the account each quarter to buy the house in three years? TM 5 -22 Slide 1 of 2

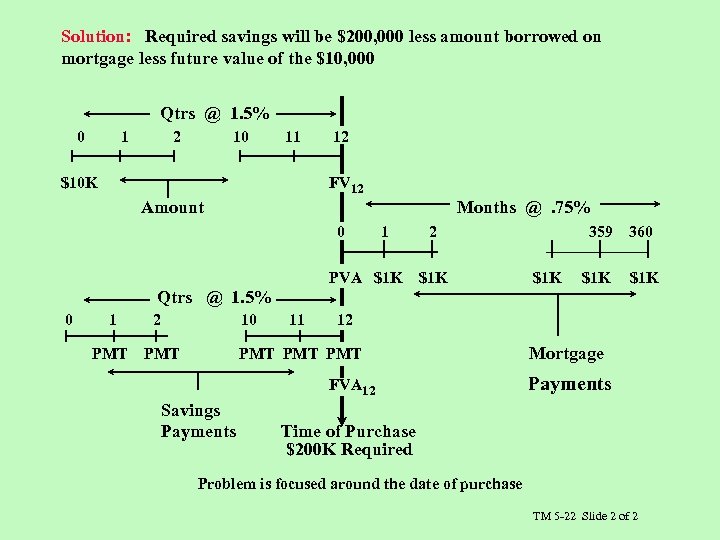Solution: Required savings will be $200, 000 less amount borrowed on mortgage less future value of the $10, 000 Qtrs @ 1. 5% 0 1 2 10 11 $10 K 12 FV 12 Amount Months @. 75% 0 1 PVA $1 K 2 $1 K 359 $1 K 360 $1 K Qtrs @ 1. 5% 0 1 2 10 PMT 11 12 PMT PMT FVA 12 Savings Payments Mortgage Payments Time of Purchase $200 K Required Problem is focused around the date of purchase TM 5 -22 Slide 2 of 2

Mortgage: k = 9%/12 =. 75%, n = 360 PMT = ($48, 000/12) x. 25 = $1, 000 PVA = PMT [PVFAk, n] = $1, 000 [PVFA. 75, 360] = $1, 000 [124. 2819] = $124, 282 Future value of the $10, 000 already in bank: k = 6%/4 = 1. 5%, n = 12 FV 12 = $10, 000 [FVF 1. 5, 12] = $10, 000 [1. 1956] = $11, 956 Savings requirement: $200, 000 - $124, 281. 90 - $11, 956. 00 = $63, 762. 10 = the FVA of savings deposits FVAn = PMT [FVFAk, n] $63, 762. 10 = PMT [FVFA 1. 5, 12] $63, 762. 10 = PMT [13. 0412] PMT = $4, 889 TM 5 -23

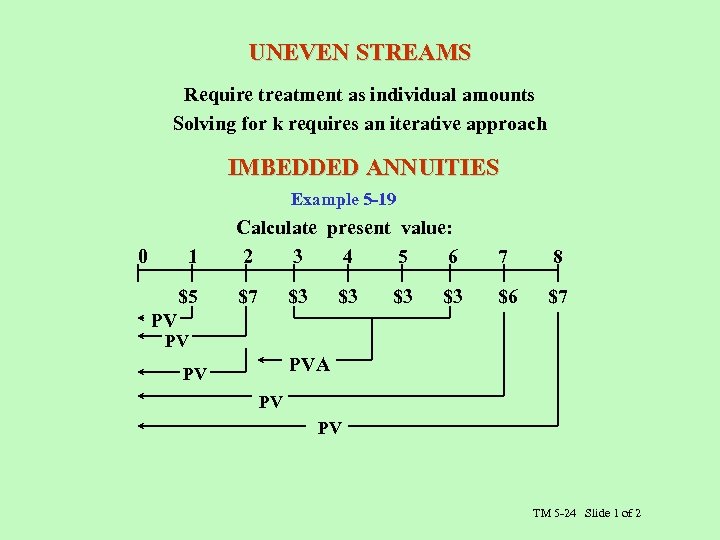UNEVEN STREAMS Require treatment as individual amounts Solving for k requires an iterative approach IMBEDDED ANNUITIES Example 5 -19 0 1 $5 Calculate present value: 2 3 4 5 6 7 8 $7 $6 $7 $3 $3 PV PV PVA PV PV PV TM 5 -24 Slide 1 of 2

Solution: Payment 1: PV = FV 1[PVF 12, 1] = $5(. 8929) = $4. 46 Payment 2: PV = FV 2[PVF 12, 2] = $7(. 7972) = $5. 58 Payment 7: PV = FV 1[PVF 12, 7] = $6(. 4523) = $2. 71 Payment 8: PV = FV 1[PVF 12, 8] = $7(. 4039) = $2. 83 Annuity: PVA = PMT [PVFA 12, 4] = $3(3. 0373) = $9. 11 and PV = FV 2[PVF 12, 2] = PVA(. 7972) = $9. 11(. 7972)= $7. 26 $22. 84 TM 5 -24 Slide 2 of 2