Chapter 5 The Firm And the Isoquant Map

Chapter 5 The Firm And the Isoquant Map

ISOQUANT- ISOCOST ANALYSIS • Isoquant • A line indicating the level of inputs required to produce a given level of output • Iso- meaning - ‘Equal’ – As in ‘Iso’-bars • -’Quant’ as in quantity • Isoquant – a line of equal quantity

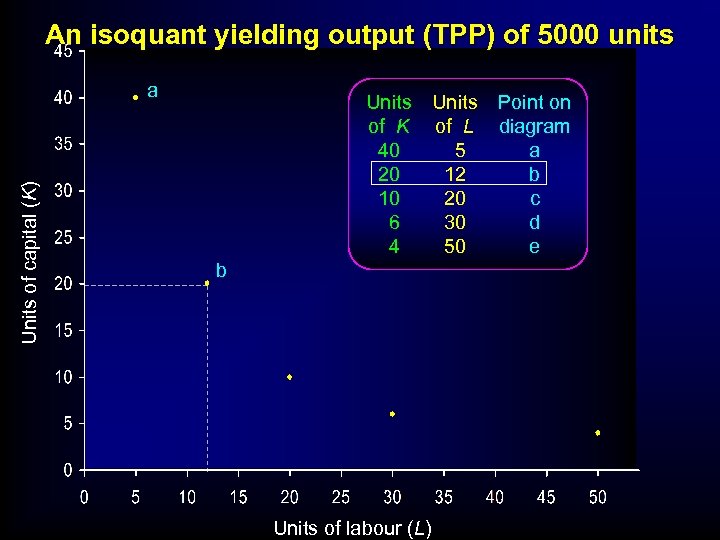An isoquant yielding output (TPP) of 5000 units Units of capital (K) a Units of K 40 20 10 6 4 b Units of labour (L) Units of L 5 12 20 30 50 Point on diagram a b c d e

ISOQUANT- ISOCOST ANALYSIS • Isoquants – their shape – diminishing marginal rate of substitution – Rate at which we can substitute capital for labour and still maintain output at the given level. MRS = DK / DL Sometimes called Marginal rate of Technical Substitution MRTS = DK / DL

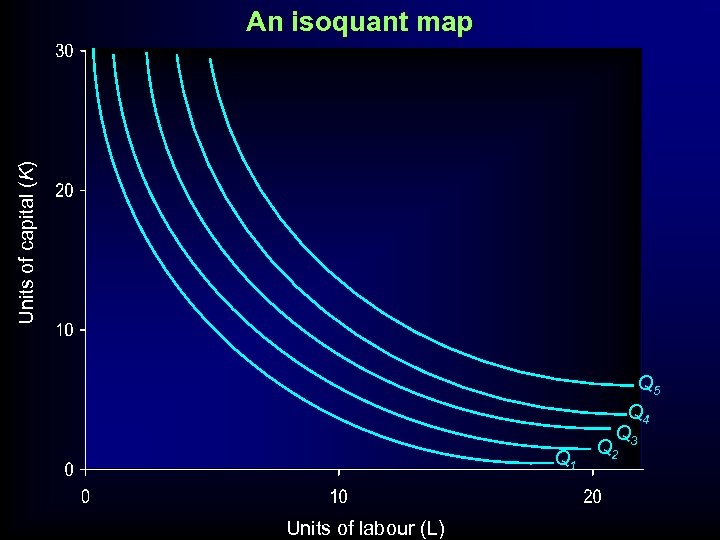Units of capital (K) An isoquant map Q 1 Units of labour (L) Q 5 Q 4 Q 3 Q 2

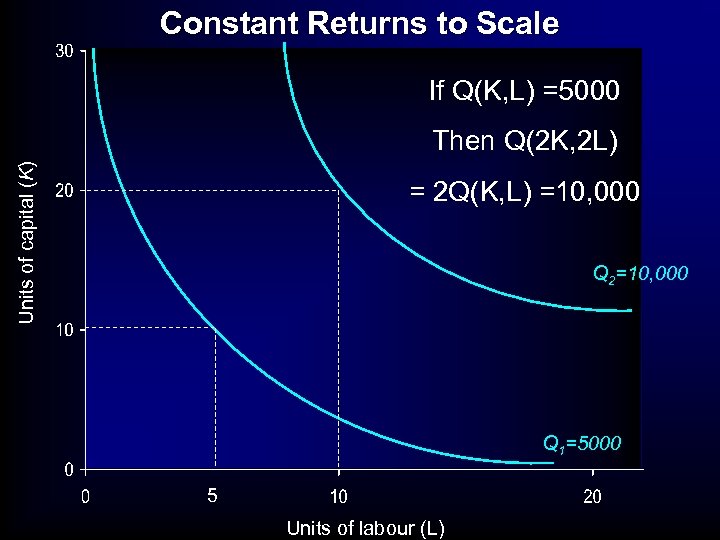Constant Returns to Scale If Q(K, L) =5000 Units of capital (K) Then Q(2 K, 2 L) = 2 Q(K, L) =10, 000 Q 2=10, 000 Q 1=5000 5 Units of labour (L)

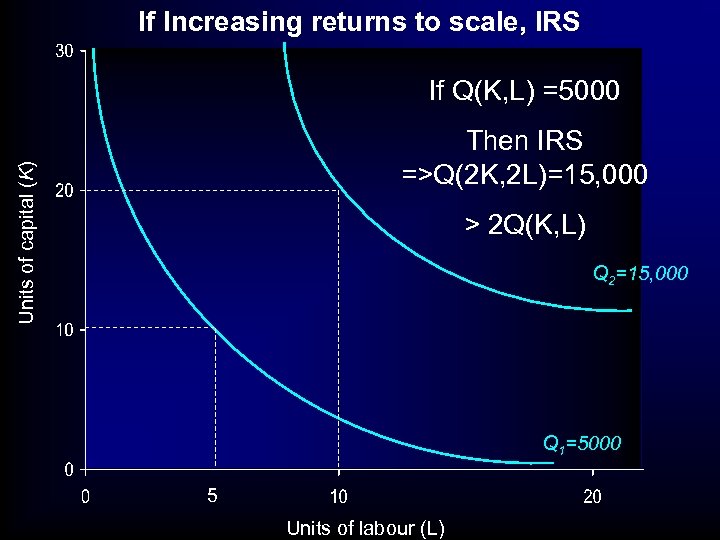If Increasing returns to scale, IRS If Q(K, L) =5000 Units of capital (K) Then IRS =>Q(2 K, 2 L)=15, 000 > 2 Q(K, L) Q 2=15, 000 Q 1=5000 5 Units of labour (L)

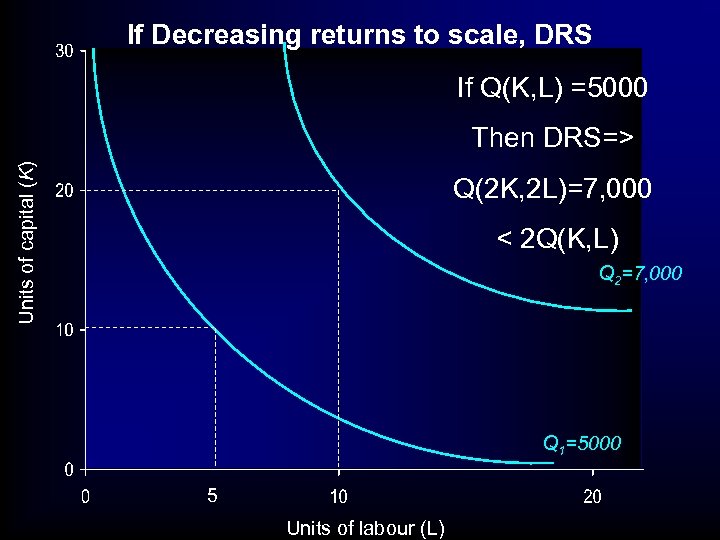If Decreasing returns to scale, DRS If Q(K, L) =5000 Units of capital (K) Then DRS=> Q(2 K, 2 L)=7, 000 < 2 Q(K, L) Q 2=7, 000 Q 1=5000 5 Units of labour (L)

ISOQUANT- ISOCOST ANALYSIS • Isoquants – isoquants and marginal returns: – Marginal Returns means changing one variable and keeping the other constant. – To see this, suppose we examine the CRS diagram again, this time with 3 isoquants, – 5000, 10, 000, and 15, 000

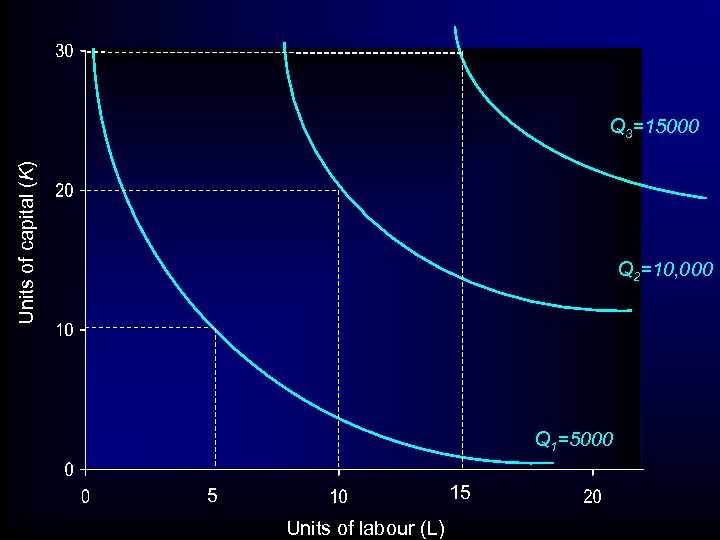Units of capital (K) Q 3=15000 Q 2=10, 000 Q 1=5000 15 5 Units of labour (L)

ISOQUANT- ISOCOST ANALYSIS • Isoquants – their shape – diminishing marginal rate of substitution – isoquants and returns to scale – isoquants and marginal returns • Isoquants- focussing on issue of efficient way to produce – E. g. Supply Tesco’s with Yogurt

ISOQUANT- ISOCOST ANALYSIS • Other focus might be on Costs: • Suppose bank or venture Capitalist will only lend you £ 300, 000 • What capital and labour will that buy you? • ISOCOST- Line of indicating set of inputs that give ‘equal’ Cost ‘

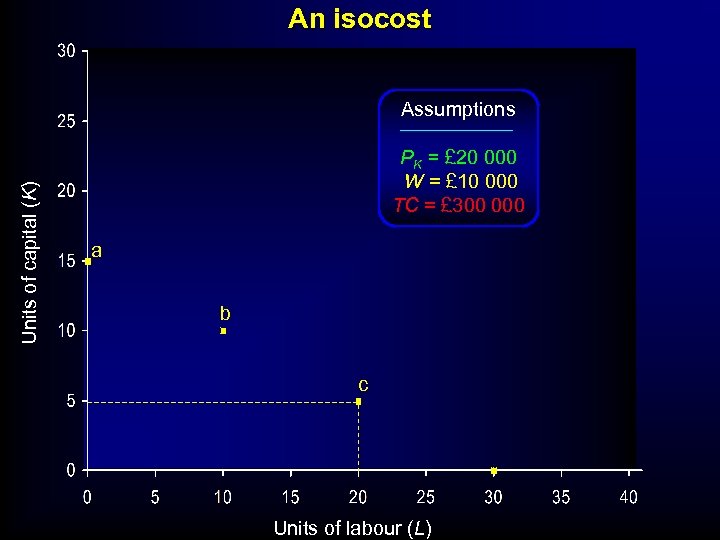An isocost Units of capital (K) Assumptions PK = £ 20 000 W = £ 10 000 TC = £ 300 000 a b c Units of labour (L)

Efficient production: • Effectively have two types of problem • 1. Least-cost combination of factors for a given output • E. g: The supplying Tesco’s problem

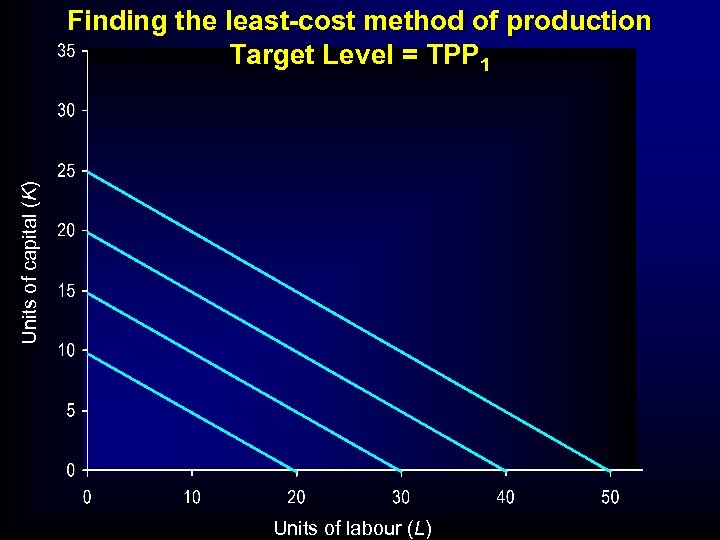Units of capital (K) Finding the least-cost method of production Target Level = TPP 1 Units of labour (L)

Efficient production: • Effectively have two types of problem • 1. Least-cost combination of factors for a given output • 2. Highest output for a given cost of production • . Here have Financial Constraint: • . E. g. : Venture Capital

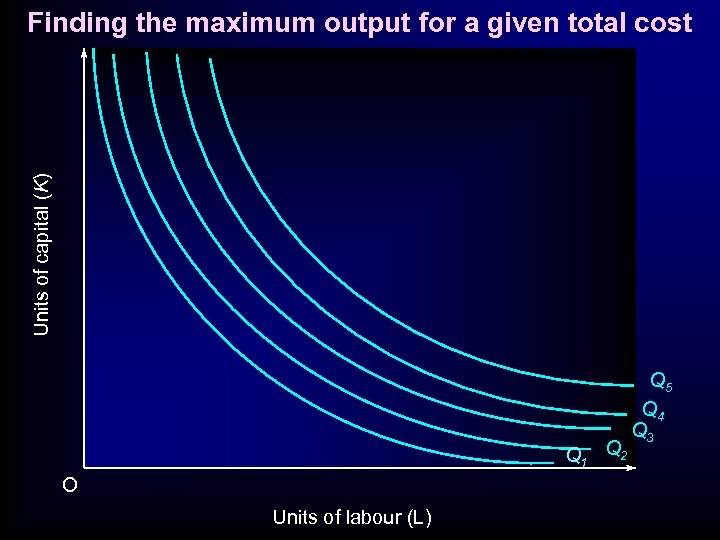Units of capital (K) Finding the maximum output for a given total cost Q 1 Q 2 O Units of labour (L) Q 5 Q 4 Q 3

Efficient production: • Effectively have two types of problem • 1. Least-cost combination of factors for a given output • 2. Highest output for a given cost of production • Comparison with Marginal Product Approach

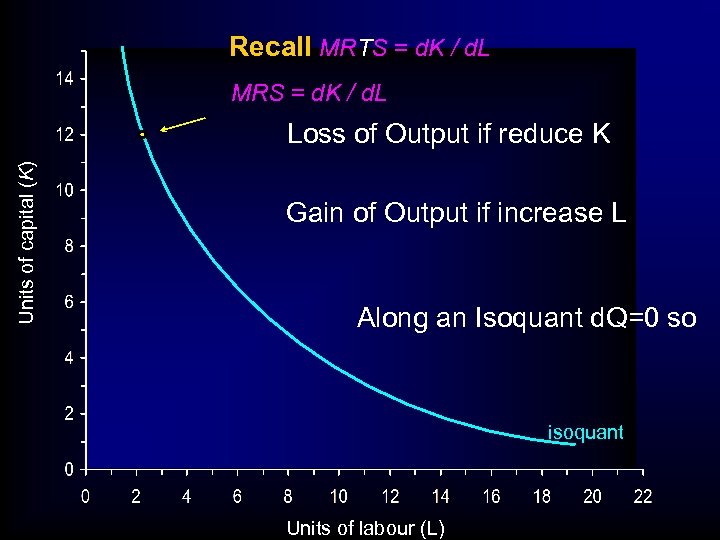Recall MRTS = d. K / d. L MRS = d. K / d. L Units of capital (K) Loss of Output if reduce K Gain of Output if increase L Along an Isoquant d. Q=0 so isoquant Units of labour (L)

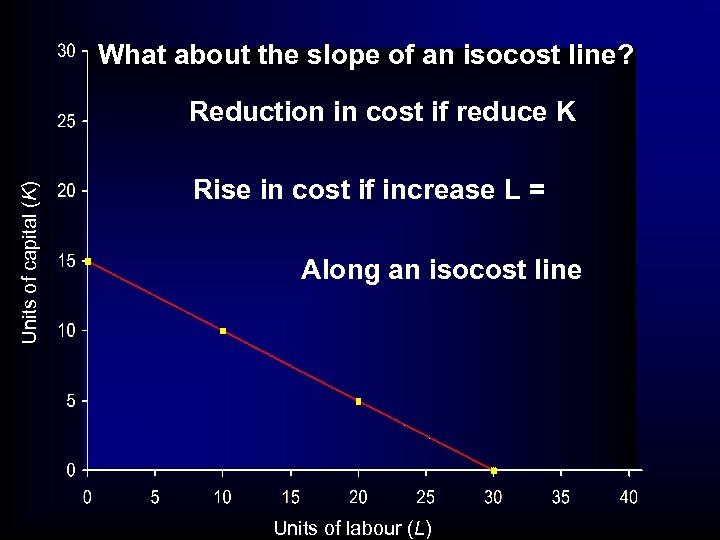What about the slope of an isocost line? Units of capital (K) Reduction in cost if reduce K Rise in cost if increase L = Along an isocost line Units of labour (L)

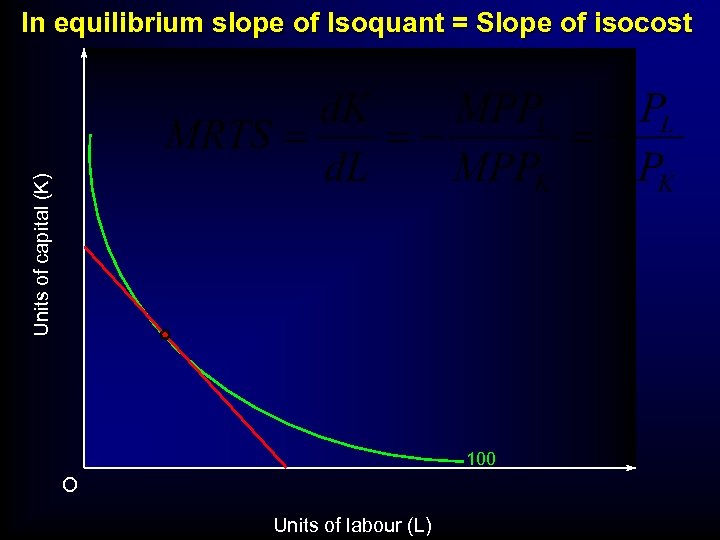Units of capital (K) In equilibrium slope of Isoquant = Slope of isocost 100 O Units of labour (L)

• Intuition is that money spent on each factor should, at the margin, yield the same additional output • Suppose not

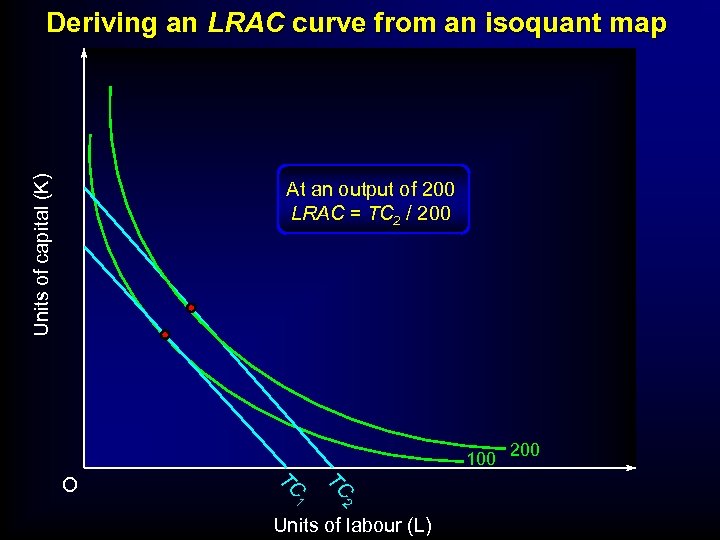Units of capital (K) Deriving an LRAC curve from an isoquant map At an output of 200 LRAC = TC 2 / 200 100 200 TC TC 1 2 O Units of labour (L)

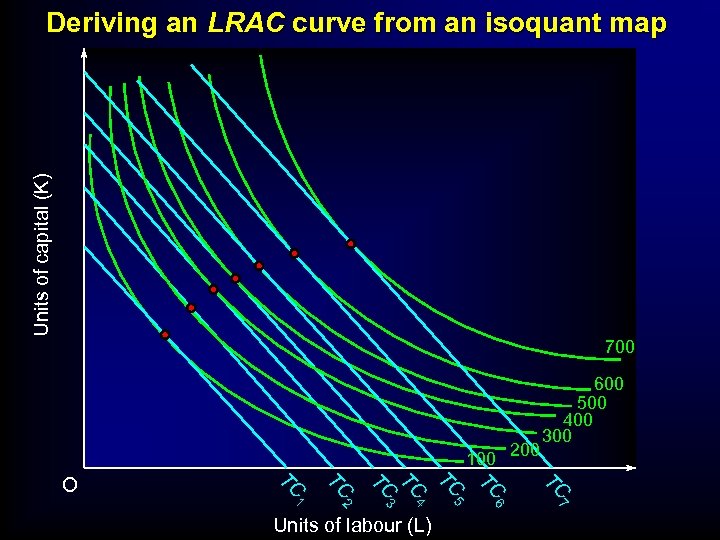Units of capital (K) Deriving an LRAC curve from an isoquant map 700 100 200 TC TC 5 6 7 Units of labour (L) TC 2 4 TC 1 TC 3 TC TC O 600 500 400 300

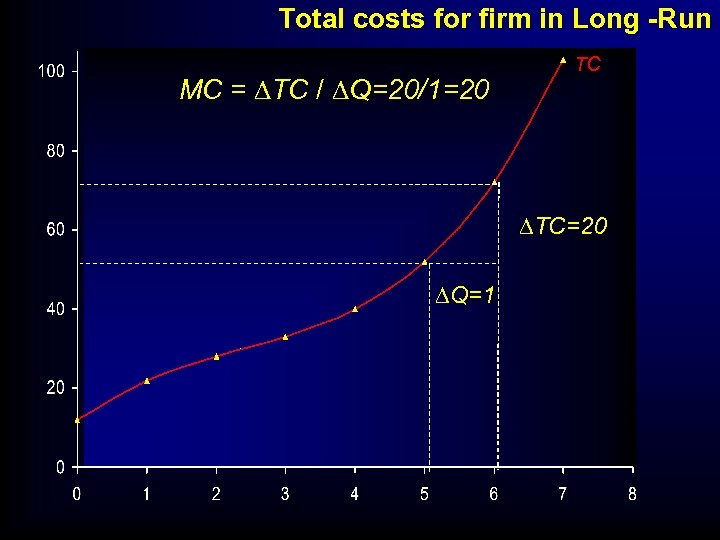Total costs for firm in Long -Run MC = DTC / DQ=20/1=20 TC DTC=20 DQ=1

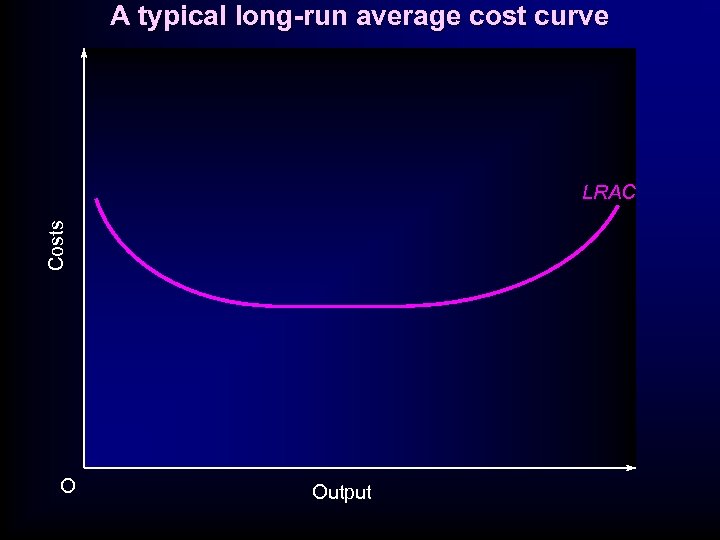A typical long-run average cost curve Costs LRAC O Output

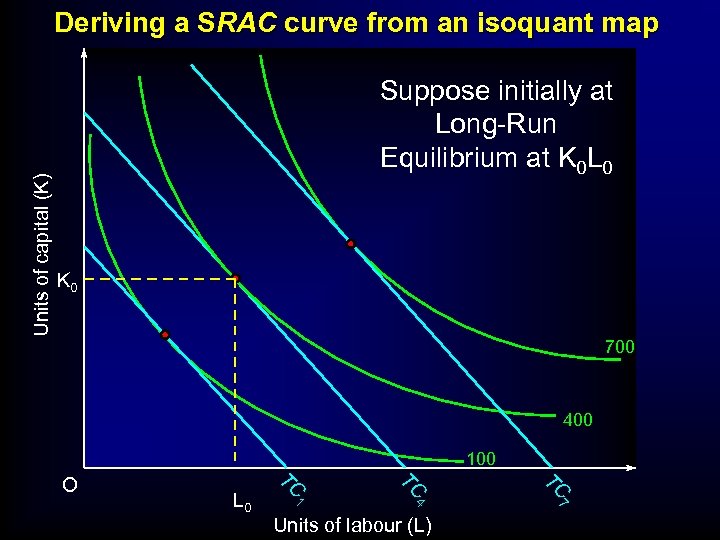Units of capital (K) Deriving a SRAC curve from an isoquant map Suppose initially at Long-Run Equilibrium at K 0 L 0 K 0 700 400 100 TC TC 1 4 7 L 0 TC O Units of labour (L)

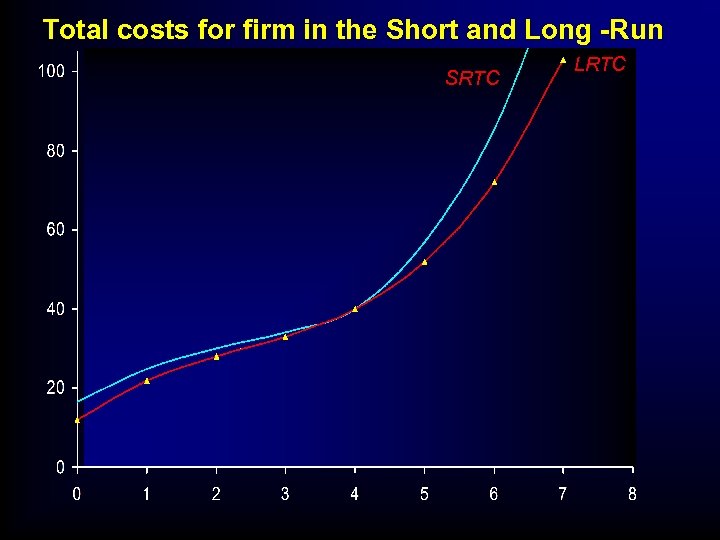Total costs for firm in the Short and Long -Run SRTC LRTC

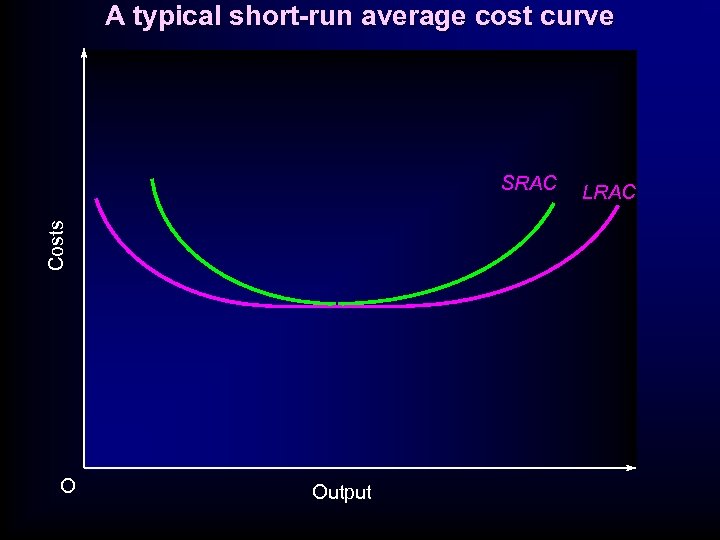A typical short-run average cost curve Costs SRAC O Output LRAC