29abd2934568f1978ff069af998c5f87.ppt
- Количество слайдов: 115
 CHAPTER 5 Ø GASES 1
CHAPTER 5 Ø GASES 1
 Characteristics of Gases Ø Ø Ø There are three phases for all substances: solid, liquid and gases. Gases are highly compressible and occupy the full volume of their containers. When a gas is subjected to pressure, its volume decreases. Gases always form homogeneous mixtures with other gases. Gases only occupy about 0. 1 % of the volume of their containers. 2
Characteristics of Gases Ø Ø Ø There are three phases for all substances: solid, liquid and gases. Gases are highly compressible and occupy the full volume of their containers. When a gas is subjected to pressure, its volume decreases. Gases always form homogeneous mixtures with other gases. Gases only occupy about 0. 1 % of the volume of their containers. 2
 Pressure Ø Pressure is the force acting on an object per unit area: Ø Units: psi pounds per square inch 3
Pressure Ø Pressure is the force acting on an object per unit area: Ø Units: psi pounds per square inch 3
 Pressure SI Units: 1 N = 1 kg. m/s 2; 1 Pa = 1 N/m 2. Ø Atmospheric pressure is measured with a barometer. Ø If a tube is inserted into a container of mercury open to the atmosphere, the mercury will rise 760 mm up the tube. Ø Standard atmospheric pressure is the pressure required to support 760 mm of Hg in a column. 4
Pressure SI Units: 1 N = 1 kg. m/s 2; 1 Pa = 1 N/m 2. Ø Atmospheric pressure is measured with a barometer. Ø If a tube is inserted into a container of mercury open to the atmosphere, the mercury will rise 760 mm up the tube. Ø Standard atmospheric pressure is the pressure required to support 760 mm of Hg in a column. 4
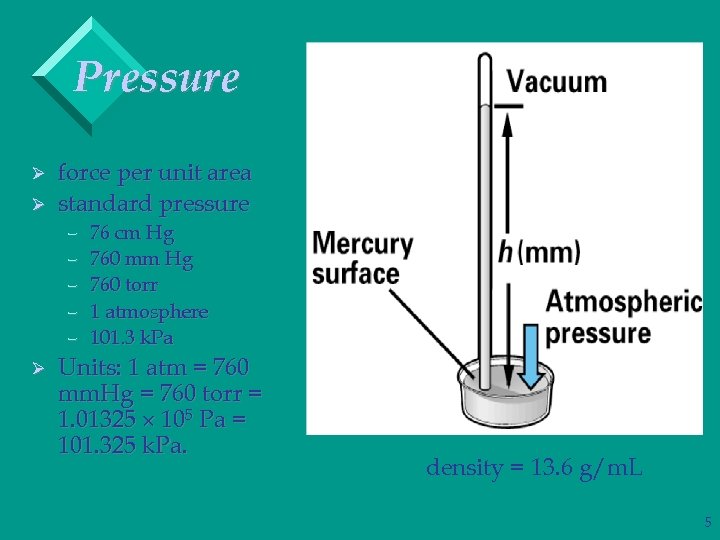 Pressure Ø Ø force per unit area standard pressure – – – Ø 76 cm Hg 760 mm Hg 760 torr 1 atmosphere 101. 3 k. Pa Units: 1 atm = 760 mm. Hg = 760 torr = 1. 01325 105 Pa = 101. 325 k. Pa. density = 13. 6 g/m. L 5
Pressure Ø Ø force per unit area standard pressure – – – Ø 76 cm Hg 760 mm Hg 760 torr 1 atmosphere 101. 3 k. Pa Units: 1 atm = 760 mm. Hg = 760 torr = 1. 01325 105 Pa = 101. 325 k. Pa. density = 13. 6 g/m. L 5
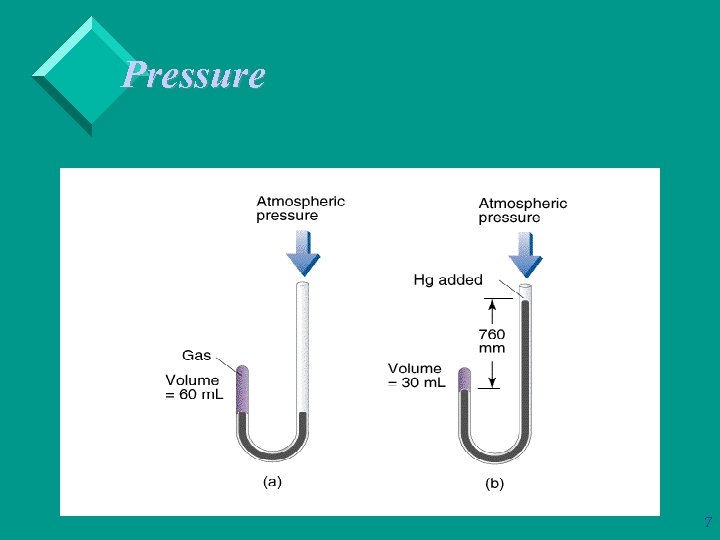
 Pressure Ø The pressures of gases not open to the atmosphere are measured in manometers. Ø A manometer consists of a bulb of gas attached to a U-tube containing Hg. 6
Pressure Ø The pressures of gases not open to the atmosphere are measured in manometers. Ø A manometer consists of a bulb of gas attached to a U-tube containing Hg. 6
 Pressure 7
Pressure 7
 Pressure If the U-tube is closed, then the pressure of the gas is the difference in height of the liquid (usually Hg). Ø If the U-tube is open to the atmosphere, a correction term needs to be added: – If Pgas < Patm then Pgas + Ph 2 = Patm. – If Pgas > Patm then Pgas = Patm + Ph 2. 8
Pressure If the U-tube is closed, then the pressure of the gas is the difference in height of the liquid (usually Hg). Ø If the U-tube is open to the atmosphere, a correction term needs to be added: – If Pgas < Patm then Pgas + Ph 2 = Patm. – If Pgas > Patm then Pgas = Patm + Ph 2. 8
 The Gas Laws Ø Ø Ø Weather balloons are used as a practical consequence to the relationship between pressure and volume of a gas. As the weather balloon ascends, the volume decreases. As the weather balloon gets further from the earth’s surface, the atmospheric pressure decreases. Boyle’s Law: the volume of a fixed quantity of gas is inversely proportional to its pressure. 9
The Gas Laws Ø Ø Ø Weather balloons are used as a practical consequence to the relationship between pressure and volume of a gas. As the weather balloon ascends, the volume decreases. As the weather balloon gets further from the earth’s surface, the atmospheric pressure decreases. Boyle’s Law: the volume of a fixed quantity of gas is inversely proportional to its pressure. 9
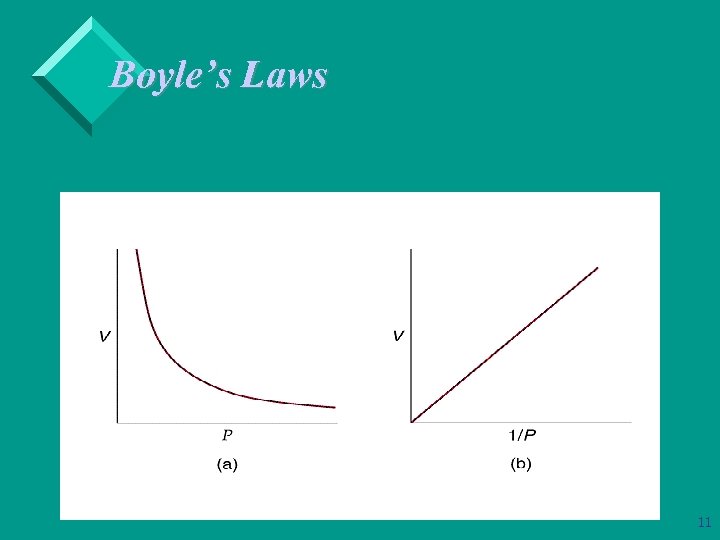
 Boyle’s Laws Ø Mathematically: Ø A plot of V versus P is a hyperbola. Ø Similarly, a plot of V versus 1/P must be a straight line passing through the origin. 10
Boyle’s Laws Ø Mathematically: Ø A plot of V versus P is a hyperbola. Ø Similarly, a plot of V versus 1/P must be a straight line passing through the origin. 10
 Boyle’s Laws 11
Boyle’s Laws 11
 Boyle’s Law Vµ 1/P Ø V= k (1/P) or PV = k Ø P 1 V 1 = k 1 P 2 V 2 = k 2 Ø k 1 = k 2 (for same sample of gas @ same T) Ø P 1 V 1 = P 2 V 2 Boyle’s Law (math form) Ø think in terms of balloons!!! Ø 12
Boyle’s Law Vµ 1/P Ø V= k (1/P) or PV = k Ø P 1 V 1 = k 1 P 2 V 2 = k 2 Ø k 1 = k 2 (for same sample of gas @ same T) Ø P 1 V 1 = P 2 V 2 Boyle’s Law (math form) Ø think in terms of balloons!!! Ø 12
 Boyle’s Law Ø Example At 250 C a sample of He has a volume of 400 m. L under a pressure of 760 torr. What volume would it occupy under a pressure of 2. 00 atm at the same T? 13
Boyle’s Law Ø Example At 250 C a sample of He has a volume of 400 m. L under a pressure of 760 torr. What volume would it occupy under a pressure of 2. 00 atm at the same T? 13
 Boyle’s Law Ø Example At 250 C a sample of He has a volume of 400 m. L under a pressure of 760 torr. What volume would it occupy under a pressure of 2. 00 atm at the same T? 14
Boyle’s Law Ø Example At 250 C a sample of He has a volume of 400 m. L under a pressure of 760 torr. What volume would it occupy under a pressure of 2. 00 atm at the same T? 14
 Boyle’s Law Ø Example At 250 C a sample of He has a volume of 400 m. L under a pressure of 760 torr. What volume would it occupy under a pressure of 2. 00 atm at the same T? 15
Boyle’s Law Ø Example At 250 C a sample of He has a volume of 400 m. L under a pressure of 760 torr. What volume would it occupy under a pressure of 2. 00 atm at the same T? 15
 The Gas Laws We know that hot air balloons expand when they are heated. Ø Charles’ Law: the volume of a fixed quantity of gas at constant pressure increases as the temperature increases. Ø Mathematically: 16
The Gas Laws We know that hot air balloons expand when they are heated. Ø Charles’ Law: the volume of a fixed quantity of gas at constant pressure increases as the temperature increases. Ø Mathematically: 16
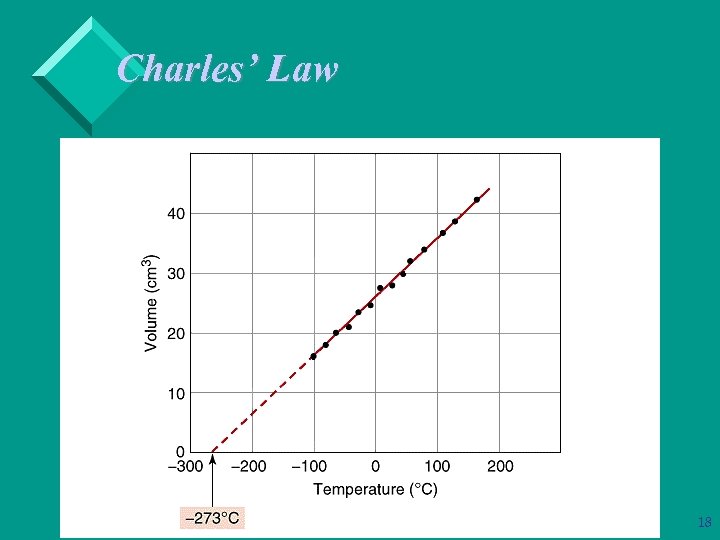
 Charles’ Law A plot of V versus T is a straight line. Ø When T is measured in C, the intercept on the temperature axis is -273. 15 C. Ø We define absolute zero, 0 K = -273. 15 C. Ø Note the value of the constant reflects the assumptions: amount of gas and pressure. 17
Charles’ Law A plot of V versus T is a straight line. Ø When T is measured in C, the intercept on the temperature axis is -273. 15 C. Ø We define absolute zero, 0 K = -273. 15 C. Ø Note the value of the constant reflects the assumptions: amount of gas and pressure. 17
 Charles’ Law 18
Charles’ Law 18
 Charles’ Law Ø volume of a gas is directly proportional to the absolute temperature at constant pressure 19
Charles’ Law Ø volume of a gas is directly proportional to the absolute temperature at constant pressure 19
 Charles’ Law Ø volume of a gas is directly proportional to the absolute temperature at constant pressure 20
Charles’ Law Ø volume of a gas is directly proportional to the absolute temperature at constant pressure 20
 Charles’ Law Ø volume of a gas is directly proportional to the absolute temperature at constant pressure 21
Charles’ Law Ø volume of a gas is directly proportional to the absolute temperature at constant pressure 21
 Charles’ Law Ø Example A sample of hydrogen, H 2, occupies 100 m. L at 250 C and 1. 00 atm. What volume would it occupy at 500 C under the same pressure? T 1 = 25 + 273 = 298 T 2 = 50 + 273 = 323 22
Charles’ Law Ø Example A sample of hydrogen, H 2, occupies 100 m. L at 250 C and 1. 00 atm. What volume would it occupy at 500 C under the same pressure? T 1 = 25 + 273 = 298 T 2 = 50 + 273 = 323 22
 Charles’ Law Ø Example: A sample of hydrogen, H 2, occupies 100 m. L at 250 C and 1. 00 atm. What volume would it occupy at 500 C under the same pressure? 23
Charles’ Law Ø Example: A sample of hydrogen, H 2, occupies 100 m. L at 250 C and 1. 00 atm. What volume would it occupy at 500 C under the same pressure? 23
 Standard Temperature & Pressure Ø STP – P = 1. 00000 atm or 101. 3 k. Pa – T = 273 K or 00 C 24
Standard Temperature & Pressure Ø STP – P = 1. 00000 atm or 101. 3 k. Pa – T = 273 K or 00 C 24
 The Gas Laws Ø Avogadro’s Hypothesis: equal volumes of gas at the same temperature and pressure will contain the same number of molecules. Ø Avogadro’s Law: the volume of gas at a given temperature and pressure is directly proportional to the number of moles of gas. 25
The Gas Laws Ø Avogadro’s Hypothesis: equal volumes of gas at the same temperature and pressure will contain the same number of molecules. Ø Avogadro’s Law: the volume of gas at a given temperature and pressure is directly proportional to the number of moles of gas. 25
 Avogadro’s Law Mathematically: V = constant n. Ø We can show that 22. 4 L of any gas at 0 C contain 6. 02 1023 gas molecules. 26
Avogadro’s Law Mathematically: V = constant n. Ø We can show that 22. 4 L of any gas at 0 C contain 6. 02 1023 gas molecules. 26
 The Ideal Gas Equation Ø Summarizing the Gas Laws Boyle: (constant n, T) Charles: V T (constant n, P) Avogadro: V n (constant P, T). Ø Combined: Ø Ideal gas equation: 27
The Ideal Gas Equation Ø Summarizing the Gas Laws Boyle: (constant n, T) Charles: V T (constant n, P) Avogadro: V n (constant P, T). Ø Combined: Ø Ideal gas equation: 27
 The Ideal Gas Equation Ø Ideal gas equation: PV = n. RT. Ø R = gas constant = 0. 08206 L • atm/mol-K. Ø We define STP (standard temperature and pressure) = 0 C, 273. 15 K, 1 atm. Ø Volume of 1 mol of gas at STP is 22. 4 L. 28
The Ideal Gas Equation Ø Ideal gas equation: PV = n. RT. Ø R = gas constant = 0. 08206 L • atm/mol-K. Ø We define STP (standard temperature and pressure) = 0 C, 273. 15 K, 1 atm. Ø Volume of 1 mol of gas at STP is 22. 4 L. 28
 Ideal Gas Law Ø R has several values depending upon the choice of units R = 8. 314 J/mol K R = 8. 314 kg m 2/s 2 K mol R = 8. 314 dm 3 k. Pa/K mol R = 1. 987 cal/K mol 29
Ideal Gas Law Ø R has several values depending upon the choice of units R = 8. 314 J/mol K R = 8. 314 kg m 2/s 2 K mol R = 8. 314 dm 3 k. Pa/K mol R = 1. 987 cal/K mol 29
 Ideal Gas Law Ø Example: What volume would 50. 0 g of ethane, C 2 H 6, occupy at 140 o. C under a pressure of 1820 torr? 30
Ideal Gas Law Ø Example: What volume would 50. 0 g of ethane, C 2 H 6, occupy at 140 o. C under a pressure of 1820 torr? 30
 Ideal Gas Law Ø Example: What volume would 50. 0 g of ethane, C 2 H 6, occupy at 140 o. C under a pressure of 1820 torr? T = 140 + 273 = 413 K P = 1820 torr (1 atm/760 torr) = 2. 39 atm 50 g (1 mol/30 g) = 1. 67 mol 31
Ideal Gas Law Ø Example: What volume would 50. 0 g of ethane, C 2 H 6, occupy at 140 o. C under a pressure of 1820 torr? T = 140 + 273 = 413 K P = 1820 torr (1 atm/760 torr) = 2. 39 atm 50 g (1 mol/30 g) = 1. 67 mol 31
 Ideal Gas Law 32
Ideal Gas Law 32
 Ideal Gas Law 33
Ideal Gas Law 33
 Ideal Gas Law Ø Example: Calculate the number of moles in, and the mass of, an 8. 96 L sample of methane, CH 4, measured at standard conditions. 34
Ideal Gas Law Ø Example: Calculate the number of moles in, and the mass of, an 8. 96 L sample of methane, CH 4, measured at standard conditions. 34
 Ideal Gas Law 35
Ideal Gas Law 35
 Ideal Gas Law Ø Example: Calculate the pressure exerted by 50. 0 g of ethane, C 2 H 6, in a 25. 0 L container at 25 o. C. 36
Ideal Gas Law Ø Example: Calculate the pressure exerted by 50. 0 g of ethane, C 2 H 6, in a 25. 0 L container at 25 o. C. 36
 Ideal Gas Law 37
Ideal Gas Law 37
 The Ideal Gas Law If PV = n. RT and n and T are constant, then PV = constant and we have Boyle’s law. Ø Other laws can be generated similarly. Ø In general, if we have a gas under two sets of conditions, then 38
The Ideal Gas Law If PV = n. RT and n and T are constant, then PV = constant and we have Boyle’s law. Ø Other laws can be generated similarly. Ø In general, if we have a gas under two sets of conditions, then 38
 Ideal Gas Law Ø Example: A sample of nitrogen gas, N 2, occupies 750 m. L at 750 C under a pressure of 810 torr. What volume would it occupy at standard conditions? 39
Ideal Gas Law Ø Example: A sample of nitrogen gas, N 2, occupies 750 m. L at 750 C under a pressure of 810 torr. What volume would it occupy at standard conditions? 39
 Ø Example: A sample of nitrogen gas, N 2, occupies 750 m. L at 750 C under a pressure of 810 torr. What volume would it occupy at standard conditions? 40
Ø Example: A sample of nitrogen gas, N 2, occupies 750 m. L at 750 C under a pressure of 810 torr. What volume would it occupy at standard conditions? 40
 Ideal Gas Laws Ø A sample of methane, CH 4, occupies 260 m. L at 32 o. C under a pressure of 0. 500 atm. At what temperature would it occupy 500 m. L under a pressure of 1200 torr? 41
Ideal Gas Laws Ø A sample of methane, CH 4, occupies 260 m. L at 32 o. C under a pressure of 0. 500 atm. At what temperature would it occupy 500 m. L under a pressure of 1200 torr? 41
 Ideal Gas Laws 42
Ideal Gas Laws 42
 Molar Mass and Density Ø Density has units of mass over volume. Ø Rearranging the ideal-gas equation with M as molar mass we get 43
Molar Mass and Density Ø Density has units of mass over volume. Ø Rearranging the ideal-gas equation with M as molar mass we get 43
 Molar Mass and Density The molar mass of a gas can be determined as follows: Volumes of Gases in Chemical Reactions Ø The ideal-gas equation relates P, V, and T to number of moles of gas. Ø The n can then be used in stoichiometric calculations. 44
Molar Mass and Density The molar mass of a gas can be determined as follows: Volumes of Gases in Chemical Reactions Ø The ideal-gas equation relates P, V, and T to number of moles of gas. Ø The n can then be used in stoichiometric calculations. 44
 Molar Mass and Density Ø Example: One mole of a gas occupies 36. 5 L and its density is 1. 36 g/L at a given T & P. (a) What is its molar mass? (b) What is its density at STP? 45
Molar Mass and Density Ø Example: One mole of a gas occupies 36. 5 L and its density is 1. 36 g/L at a given T & P. (a) What is its molar mass? (b) What is its density at STP? 45
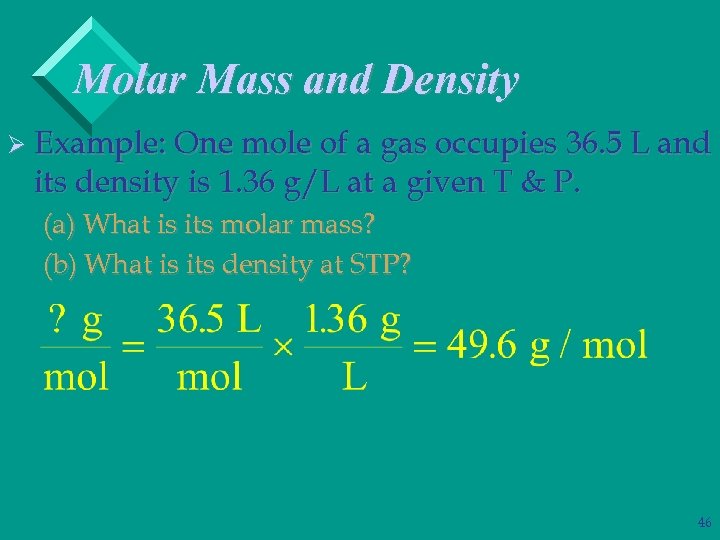 Molar Mass and Density Ø Example: One mole of a gas occupies 36. 5 L and its density is 1. 36 g/L at a given T & P. (a) What is its molar mass? (b) What is its density at STP? 46
Molar Mass and Density Ø Example: One mole of a gas occupies 36. 5 L and its density is 1. 36 g/L at a given T & P. (a) What is its molar mass? (b) What is its density at STP? 46
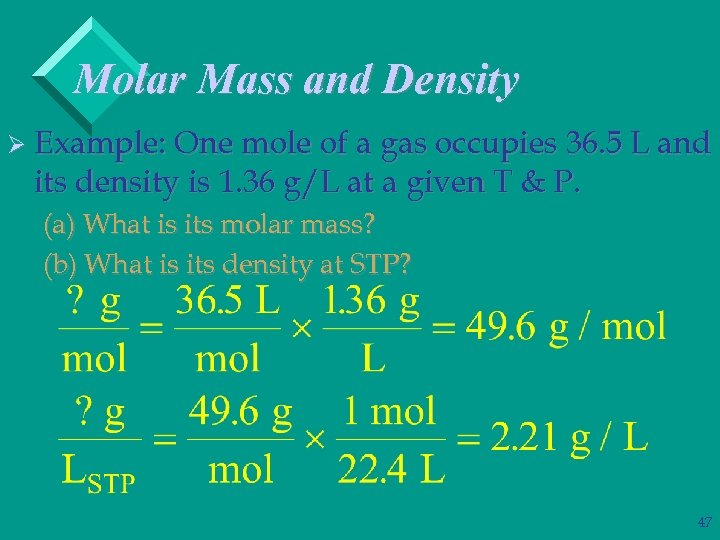 Molar Mass and Density Ø Example: One mole of a gas occupies 36. 5 L and its density is 1. 36 g/L at a given T & P. (a) What is its molar mass? (b) What is its density at STP? 47
Molar Mass and Density Ø Example: One mole of a gas occupies 36. 5 L and its density is 1. 36 g/L at a given T & P. (a) What is its molar mass? (b) What is its density at STP? 47
 Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A compound that contains only carbon & hydrogen is 80. 0% C and 20. 0% H by mass. At STP 546 m. L of the gas has a mass of 0. 732 g. What is the molecular (true) formula for the compound? 100 g of compound contains: 80 g of C & 20 g of H 48
Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A compound that contains only carbon & hydrogen is 80. 0% C and 20. 0% H by mass. At STP 546 m. L of the gas has a mass of 0. 732 g. What is the molecular (true) formula for the compound? 100 g of compound contains: 80 g of C & 20 g of H 48
 Determination of Molar Mass & Formulas of Gaseous Compounds 49
Determination of Molar Mass & Formulas of Gaseous Compounds 49
 Determination of Molar Mass & Formulas of Gaseous Compounds 50
Determination of Molar Mass & Formulas of Gaseous Compounds 50
 Determination of Molar Mass & Formulas of Gaseous Compounds 51
Determination of Molar Mass & Formulas of Gaseous Compounds 51
 Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A 1. 74 g sample of a compound that contains only carbon & hydrogen contains 1. 44 g of C and 0. 300 g of H. At STP 101 m. L of the gas has a mass of 0. 262 gram. What is its molecular (true) formula? 52
Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A 1. 74 g sample of a compound that contains only carbon & hydrogen contains 1. 44 g of C and 0. 300 g of H. At STP 101 m. L of the gas has a mass of 0. 262 gram. What is its molecular (true) formula? 52
 Determination of Molar Mass & Formulas of Gaseous Compounds 53
Determination of Molar Mass & Formulas of Gaseous Compounds 53
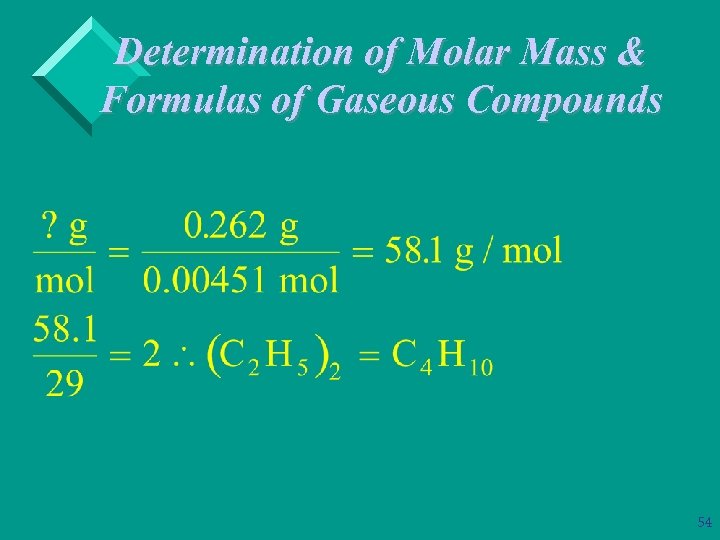 Determination of Molar Mass & Formulas of Gaseous Compounds 54
Determination of Molar Mass & Formulas of Gaseous Compounds 54
 Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A 250 m. L flask contains 0. 423 g of vapor at 1000 C and 746 torr. What is molar mass of compound? 55
Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A 250 m. L flask contains 0. 423 g of vapor at 1000 C and 746 torr. What is molar mass of compound? 55
 Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A 250 m. L flask contains 0. 423 g of vapor at 1000 C and 746 torr. What is molar mass of compound? 56
Determination of Molar Mass & Formulas of Gaseous Compounds Ø Example: A 250 m. L flask contains 0. 423 g of vapor at 1000 C and 746 torr. What is molar mass of compound? 56
 Gas Mixtures and Partial Pressures Ø Since gas molecules are so far apart, we can assume they behave independently. Ø Dalton’s Law: in a gas mixture the total pressure is given by the sum of partial pressures of each component: Pt = P 1 + P 2 + P 3 + … 57
Gas Mixtures and Partial Pressures Ø Since gas molecules are so far apart, we can assume they behave independently. Ø Dalton’s Law: in a gas mixture the total pressure is given by the sum of partial pressures of each component: Pt = P 1 + P 2 + P 3 + … 57
 Gas Mixtures and Partial Pressures Each gas obeys the ideal gas equation: Ø Combining equations: 58
Gas Mixtures and Partial Pressures Each gas obeys the ideal gas equation: Ø Combining equations: 58
 Mole Fractions Let ni be the number of moles of gas i exerting a partial pressure Pi, then P i = i. P t where i is the mole fraction (ni/nt). 59
Mole Fractions Let ni be the number of moles of gas i exerting a partial pressure Pi, then P i = i. P t where i is the mole fraction (ni/nt). 59
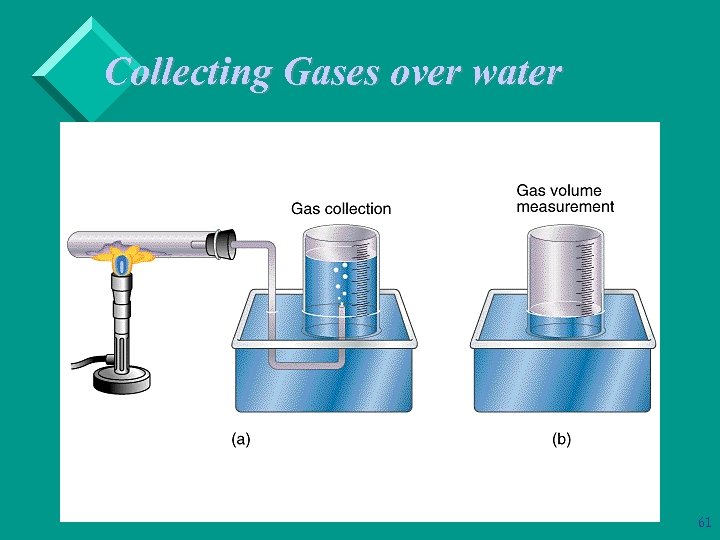
 Collecting Gases over water Ø It is common to synthesize gases and collect them by displacing a volume of water. Ø To calculate the amount of gas produced, we need to correct for the partial pressure of the water: Ptotal = Pgas + Pwater 60
Collecting Gases over water Ø It is common to synthesize gases and collect them by displacing a volume of water. Ø To calculate the amount of gas produced, we need to correct for the partial pressure of the water: Ptotal = Pgas + Pwater 60
 Collecting Gases over water 61
Collecting Gases over water 61
 Dalton’s Law of Partial Pressures Ø Example: If 100 m. L of hydrogen, measured at 250 C & 3. 00 atm pressure, and 100 m. L of oxygen, measured at 250 C & 2. 00 atm pressure, were forced into one of the containers at 250 C, what would be the pressure of the mixture of gases? 62
Dalton’s Law of Partial Pressures Ø Example: If 100 m. L of hydrogen, measured at 250 C & 3. 00 atm pressure, and 100 m. L of oxygen, measured at 250 C & 2. 00 atm pressure, were forced into one of the containers at 250 C, what would be the pressure of the mixture of gases? 62
 Dalton’s Law of Partial Pressures Ø Example: If 100 m. L of hydrogen, measured at 250 C & 3. 00 atm pressure, and 100 m. L of oxygen, measured at 250 C & 2. 00 atm pressure, were forced into one of the containers at 250 C, what would be the pressure of the mixture of gases? 63
Dalton’s Law of Partial Pressures Ø Example: If 100 m. L of hydrogen, measured at 250 C & 3. 00 atm pressure, and 100 m. L of oxygen, measured at 250 C & 2. 00 atm pressure, were forced into one of the containers at 250 C, what would be the pressure of the mixture of gases? 63
 Vapor Pressure Ø Pressure exerted by gas over the liquid at equilibrium. 64
Vapor Pressure Ø Pressure exerted by gas over the liquid at equilibrium. 64
 Vapor Pressure Ø Example: A sample of hydrogen was collected by displacement of water at 250 C. The atmospheric pressure was 748 torr. What pressure would the dry hydrogen exert in the same container? 65
Vapor Pressure Ø Example: A sample of hydrogen was collected by displacement of water at 250 C. The atmospheric pressure was 748 torr. What pressure would the dry hydrogen exert in the same container? 65
 Vapor Pressure Ø Example: A sample of hydrogen was collected by displacement of water at 250 C. The atmospheric pressure was 748 torr. What pressure would the dry hydrogen exert in the same container? 66
Vapor Pressure Ø Example: A sample of hydrogen was collected by displacement of water at 250 C. The atmospheric pressure was 748 torr. What pressure would the dry hydrogen exert in the same container? 66
 Vapor Pressure Ø Example: A sample of oxygen was collected by displacement of water. The oxygen occupied 742 m. L at 27 o. C. The barometric pressure was 753 torr. What volume would the dry oxygen occupy at STP? 67
Vapor Pressure Ø Example: A sample of oxygen was collected by displacement of water. The oxygen occupied 742 m. L at 27 o. C. The barometric pressure was 753 torr. What volume would the dry oxygen occupy at STP? 67
 Vapor Pressure 68
Vapor Pressure 68
 Kinetic-Molecular Theory Ø Ø Ø Theory developed to explain gas behavior. Theory of moving molecules. Assumptions: – – Gases consist of a large number of molecules in constant random motion. Volume of individual molecules negligible compared to volume of container. Intermolecular forces (forces between gas molecules) negligible. Energy can be transferred between molecules, but total kinetic energy is constant at constant temperature. – Average kinetic energy of molecules is proportional to temperature. 69
Kinetic-Molecular Theory Ø Ø Ø Theory developed to explain gas behavior. Theory of moving molecules. Assumptions: – – Gases consist of a large number of molecules in constant random motion. Volume of individual molecules negligible compared to volume of container. Intermolecular forces (forces between gas molecules) negligible. Energy can be transferred between molecules, but total kinetic energy is constant at constant temperature. – Average kinetic energy of molecules is proportional to temperature. 69
 Kinetic Molecular Theory Ø Postulate 1 – gases are discrete molecules that are far apart – have few intermolecular attractions – molecular volume small compared to gas’s volume Ø Proof - Gases are easily compressible. 70
Kinetic Molecular Theory Ø Postulate 1 – gases are discrete molecules that are far apart – have few intermolecular attractions – molecular volume small compared to gas’s volume Ø Proof - Gases are easily compressible. 70
 Kinetic Molecular Theory Ø Postulate 2 – molecules are in constant straight line motion – varying velocities – molecules have elastic collisions Ø Proof - A sealed, confined gas exhibits no pressure drop over time. 71
Kinetic Molecular Theory Ø Postulate 2 – molecules are in constant straight line motion – varying velocities – molecules have elastic collisions Ø Proof - A sealed, confined gas exhibits no pressure drop over time. 71
 Kinetic Molecular Theory Ø Postulate 3 – kinetic energy is proportional to absolute T – average kinetic energies of molecules of different gases are equal at a given T Ø Proof - Motion increases as temperature increases. 72
Kinetic Molecular Theory Ø Postulate 3 – kinetic energy is proportional to absolute T – average kinetic energies of molecules of different gases are equal at a given T Ø Proof - Motion increases as temperature increases. 72
 Kinetic Molecular Theory Ø Boyle’s & Dalton’s Law – P µ 1/V as V increases collisions decrease so P drops – Ptotal = PA + PB + PC +. . . because few intermolecular attractions Ø Charles’ Law – V µ T increased T raises molecular velocities, V increases to keep P constant 73
Kinetic Molecular Theory Ø Boyle’s & Dalton’s Law – P µ 1/V as V increases collisions decrease so P drops – Ptotal = PA + PB + PC +. . . because few intermolecular attractions Ø Charles’ Law – V µ T increased T raises molecular velocities, V increases to keep P constant 73
 Kinetic-Molecular Theory Ø Ø Kinetic molecular theory gives us an understanding of pressure and temperature on the molecular level. Pressure of a gas results from the number of collisions per unit time on the walls of container. 74
Kinetic-Molecular Theory Ø Ø Kinetic molecular theory gives us an understanding of pressure and temperature on the molecular level. Pressure of a gas results from the number of collisions per unit time on the walls of container. 74
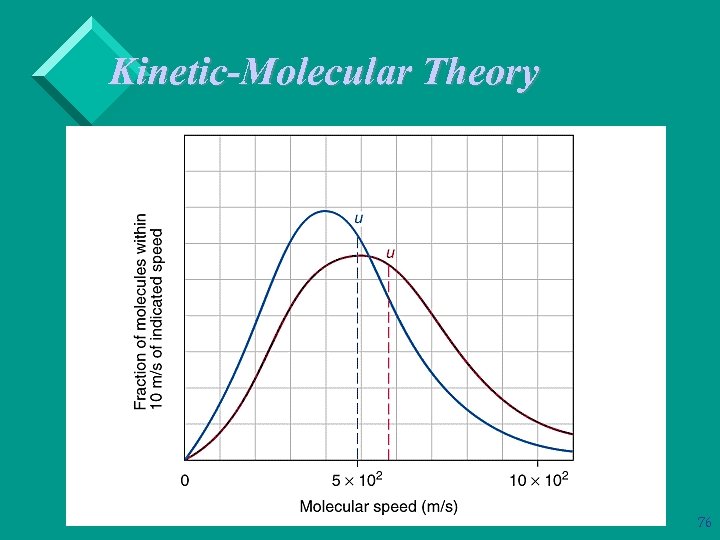
 Kinetic-Molecular Theory Ø Ø Ø Magnitude of pressure given by how often and how hard the molecules strike. Gas molecules have an average kinetic energy. Each molecule has a different energy. There is a spread of individual energies of gas molecules in any sample of gas. As the temperature increases, the average kinetic energy of the gas molecules increases. 75
Kinetic-Molecular Theory Ø Ø Ø Magnitude of pressure given by how often and how hard the molecules strike. Gas molecules have an average kinetic energy. Each molecule has a different energy. There is a spread of individual energies of gas molecules in any sample of gas. As the temperature increases, the average kinetic energy of the gas molecules increases. 75
 Kinetic-Molecular Theory 76
Kinetic-Molecular Theory 76
 Kinetic-Molecular Theory Ø As kinetic energy increases, the velocity of the gas molecules increases. Ø Root mean square speed, u, is the speed of a gas molecule having average kinetic energy. Ø Average kinetic energy, , is related to root mean square speed: = ½mu 2 77
Kinetic-Molecular Theory Ø As kinetic energy increases, the velocity of the gas molecules increases. Ø Root mean square speed, u, is the speed of a gas molecule having average kinetic energy. Ø Average kinetic energy, , is related to root mean square speed: = ½mu 2 77
 Kinetic-Molecular Theory As volume increases at constant temperature, the average kinetic of the gas remains constant. Therefore, u is constant. However, volume increases so the gas molecules have to travel further to hit the walls of the container. Therefore, pressure decreases. Ø If temperature increases at constant volume, the average kinetic energy of the gas molecules increases. Therefore, there are more collisions with the container walls and the pressure increases. 78
Kinetic-Molecular Theory As volume increases at constant temperature, the average kinetic of the gas remains constant. Therefore, u is constant. However, volume increases so the gas molecules have to travel further to hit the walls of the container. Therefore, pressure decreases. Ø If temperature increases at constant volume, the average kinetic energy of the gas molecules increases. Therefore, there are more collisions with the container walls and the pressure increases. 78
 Effusion & Diffusion Ø diffusion - intermingling of gases Ø effusion - gases pass through porous containers Ø rates are inversely proportional to square roots of molecular weights or densities 79
Effusion & Diffusion Ø diffusion - intermingling of gases Ø effusion - gases pass through porous containers Ø rates are inversely proportional to square roots of molecular weights or densities 79
 Effusion & Diffusion effusion - gases pass through porous containers – Effusion is the escape of a gas through a tiny hole (a balloon will deflate over time due to effusion). Ø rates are inversely proportional to square roots of molecular weights or densities 80
Effusion & Diffusion effusion - gases pass through porous containers – Effusion is the escape of a gas through a tiny hole (a balloon will deflate over time due to effusion). Ø rates are inversely proportional to square roots of molecular weights or densities 80
 Effusion & Diffusion Ø Ø Diffusion of a gas is the spread of the gas through space. Diffusion is faster for light gas molecules. Diffusion is significantly slower than rms speed (consider someone opening a perfume bottle: it takes while to detect the odor but rms speed at 25 C is about 1150 mi/hr). Diffusion is slowed by gas molecules colliding with each other. Average distance of a gas molecule between collisions is called mean free path. 81
Effusion & Diffusion Ø Ø Diffusion of a gas is the spread of the gas through space. Diffusion is faster for light gas molecules. Diffusion is significantly slower than rms speed (consider someone opening a perfume bottle: it takes while to detect the odor but rms speed at 25 C is about 1150 mi/hr). Diffusion is slowed by gas molecules colliding with each other. Average distance of a gas molecule between collisions is called mean free path. 81
 Effusion & Diffusion At sea level, mean free path is about 6 10 -6 cm. 82
Effusion & Diffusion At sea level, mean free path is about 6 10 -6 cm. 82
 Effusion & Diffusion Ø Calculate the ratio of the rate of effusion of He to that of sulfur dioxide, SO 2, at the same T & P. 83
Effusion & Diffusion Ø Calculate the ratio of the rate of effusion of He to that of sulfur dioxide, SO 2, at the same T & P. 83
 Effusion & Diffusion Ø Calculate the ratio of the rate of effusion of He to that of sulfur dioxide, SO 2, at the same T & P. 84
Effusion & Diffusion Ø Calculate the ratio of the rate of effusion of He to that of sulfur dioxide, SO 2, at the same T & P. 84
 Effusion & Diffusion Ø Example: A sample of hydrogen, H 2, was found to effuse through a pinhole 5. 2 times as rapidly as the same volume of unkown gas ( at the same T & P). What is the molecular weight of the unknown gas? 85
Effusion & Diffusion Ø Example: A sample of hydrogen, H 2, was found to effuse through a pinhole 5. 2 times as rapidly as the same volume of unkown gas ( at the same T & P). What is the molecular weight of the unknown gas? 85
 Effusion & Diffusion 86
Effusion & Diffusion 86
 Average Speed Ø Ø As kinetic energy increases, the velocity of the gas molecules increases. Average kinetic energy of a gas is related to its mass: Ø = ½mu 2 87
Average Speed Ø Ø As kinetic energy increases, the velocity of the gas molecules increases. Average kinetic energy of a gas is related to its mass: Ø = ½mu 2 87
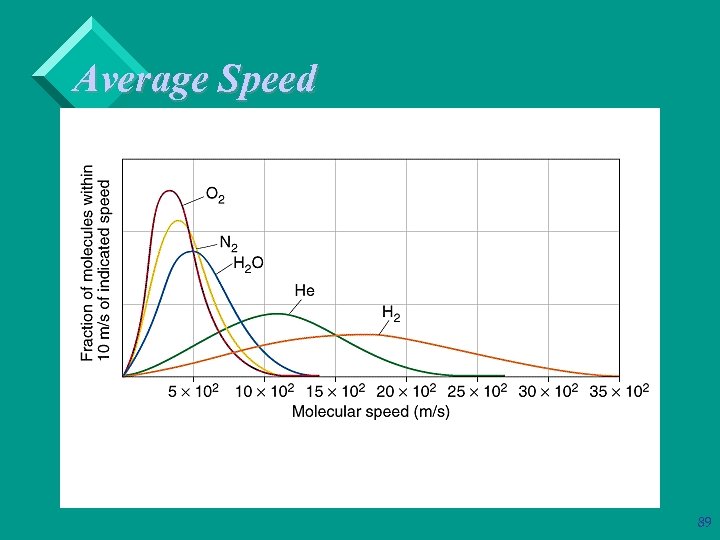
 Average Speed Ø Ø Ø Consider two gases at the same temperature: the lighter gas has a higher rms than the heavier gas. Mathematically: The lower the molar mass, M, the higher the rms for that gas at a constant temperature. 88
Average Speed Ø Ø Ø Consider two gases at the same temperature: the lighter gas has a higher rms than the heavier gas. Mathematically: The lower the molar mass, M, the higher the rms for that gas at a constant temperature. 88
 Average Speed 89
Average Speed 89
 Average Speed Ø R = 8. 314 kg m 2/s 2 K mol Ø M must be in kg/mol 90
Average Speed Ø R = 8. 314 kg m 2/s 2 K mol Ø M must be in kg/mol 90
 Average Speed Ø What is velocity of N 2 molecules at room T, 250 C? 91
Average Speed Ø What is velocity of N 2 molecules at room T, 250 C? 91
 Average Speed Ø What is the velocity of He at room T, 250 C? 92
Average Speed Ø What is the velocity of He at room T, 250 C? 92
 Average Speed Ø What is the velocity of He at room T, 250 C? 93
Average Speed Ø What is the velocity of He at room T, 250 C? 93
 Real Gases Ø real gases behave ideally at ordinary T’s & P’s Ø at low T and high P - large deviations – molecules are on top of one another – molecular interactions become important 94
Real Gases Ø real gases behave ideally at ordinary T’s & P’s Ø at low T and high P - large deviations – molecules are on top of one another – molecular interactions become important 94
 Real Gases Ø Ø Ø As the pressure on a gas increases, the molecules are forced closer together. As the molecules get closer together, the volume of the container gets smaller. The smaller the container, the more space the gas molecules begin to occupy. Therefore, the higher the pressure, the less the gas resembles an ideal gas. As the gas molecules get closer together, the smaller the intermolecular distance. 95
Real Gases Ø Ø Ø As the pressure on a gas increases, the molecules are forced closer together. As the molecules get closer together, the volume of the container gets smaller. The smaller the container, the more space the gas molecules begin to occupy. Therefore, the higher the pressure, the less the gas resembles an ideal gas. As the gas molecules get closer together, the smaller the intermolecular distance. 95
 Real Gases 96
Real Gases 96
 Real Gases 97
Real Gases 97
 Real Gases Ø Ø Ø The smaller the distance between gas molecules, the more likely attractive forces will develop between the molecules. Therefore, the less the gas resembles and ideal gas. As temperature increases, the gas molecules move faster and further apart. Also, higher temperatures mean more energy available to break intermolecular forces. Therefore, the higher the temperature, the more ideal the gas. 98
Real Gases Ø Ø Ø The smaller the distance between gas molecules, the more likely attractive forces will develop between the molecules. Therefore, the less the gas resembles and ideal gas. As temperature increases, the gas molecules move faster and further apart. Also, higher temperatures mean more energy available to break intermolecular forces. Therefore, the higher the temperature, the more ideal the gas. 98
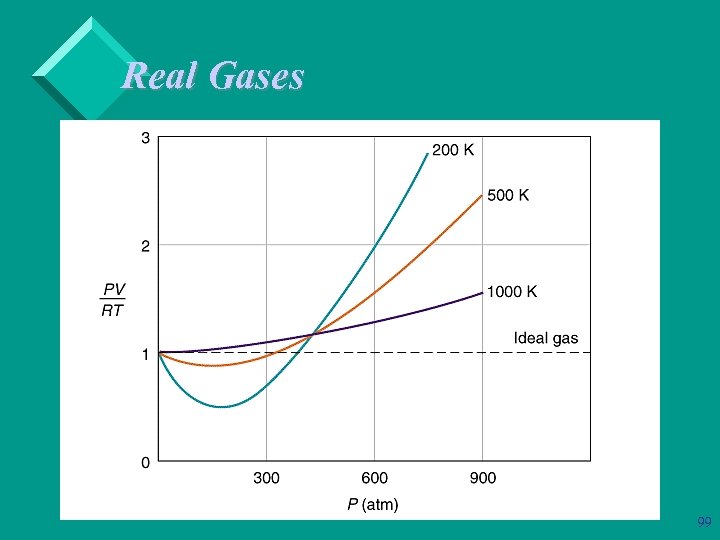 Real Gases 99
Real Gases 99
 Real Gases Ø van der Waals’s equation a & b are van der Waal’s constants different values for each gas 100
Real Gases Ø van der Waals’s equation a & b are van der Waal’s constants different values for each gas 100
 Real Gases Ø van der Waals’s equation – a accounts for intermolecular attractions – b accounts for volume of gas molecules – large V’s a & b reduce to small quantities Ø van der Waal’s equation reduces to ideal gas law at high temperatures and low pressures 101
Real Gases Ø van der Waals’s equation – a accounts for intermolecular attractions – b accounts for volume of gas molecules – large V’s a & b reduce to small quantities Ø van der Waal’s equation reduces to ideal gas law at high temperatures and low pressures 101
 Real Gases Ø attractive forces in nonpolar gases – London Forces • • noble gases- instantaneous induced dipole moments Chapter 9 Ø attractive forces in polar gases – dipole-dipole or H-bonds • • water molecules can H-bond why ice floats - Chapter 9 102
Real Gases Ø attractive forces in nonpolar gases – London Forces • • noble gases- instantaneous induced dipole moments Chapter 9 Ø attractive forces in polar gases – dipole-dipole or H-bonds • • water molecules can H-bond why ice floats - Chapter 9 102
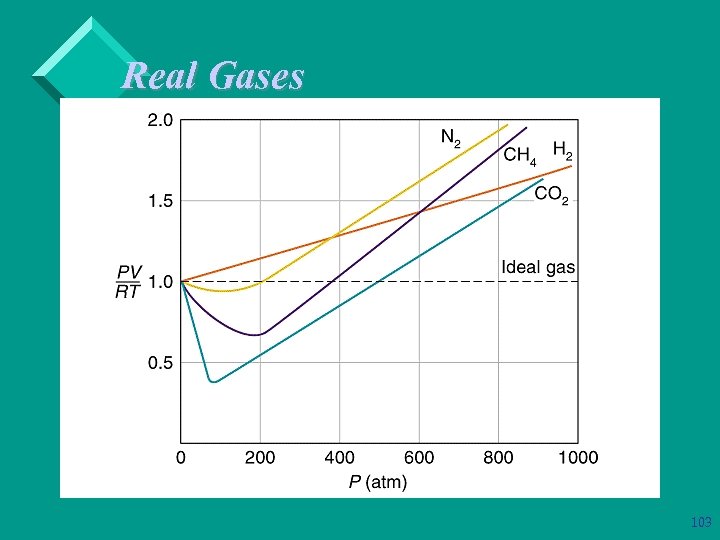 Real Gases 103
Real Gases 103
 Real Gases Ø Example: Calculate the pressure exerted by 84. 0 g of ammonia, NH 3, in a 5. 00 L at 2000 C using the ideal gas law. 104
Real Gases Ø Example: Calculate the pressure exerted by 84. 0 g of ammonia, NH 3, in a 5. 00 L at 2000 C using the ideal gas law. 104
 Real Gases 105
Real Gases 105
 Real Gases Ø Example: Solve previous example using the van der Waal’s equation. 106
Real Gases Ø Example: Solve previous example using the van der Waal’s equation. 106
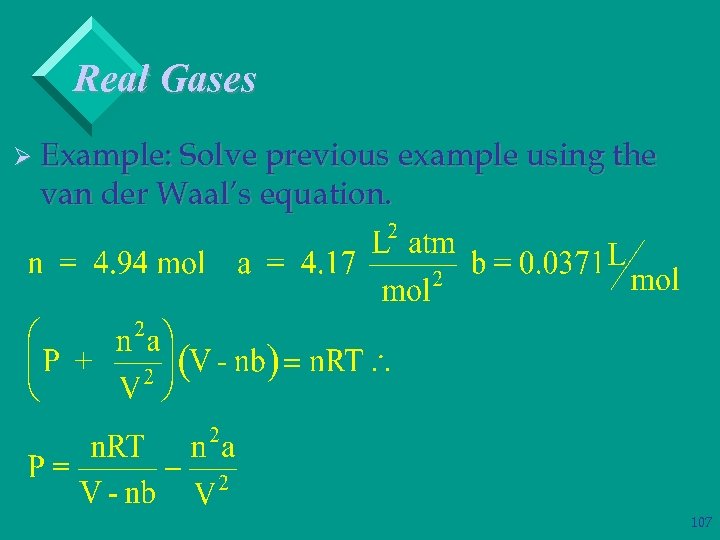 Real Gases Ø Example: Solve previous example using the van der Waal’s equation. 107
Real Gases Ø Example: Solve previous example using the van der Waal’s equation. 107
 Real Gases 108
Real Gases 108
 We can’t forget about moles! Ø Example: What volume of oxygen measured at STP, can be produced by thermal decomposition of 120 g of KCl. O 3? 109
We can’t forget about moles! Ø Example: What volume of oxygen measured at STP, can be produced by thermal decomposition of 120 g of KCl. O 3? 109
 Mass-Volume Relationships in Reactions Involving Gases Ø 2 mol 3 mol Ø 2(122. 6 g) 2(74. 6 g) 3(32 g) 3 moles of oxygen equal to 3(22. 4 L) or 67. 2 L at STP 110
Mass-Volume Relationships in Reactions Involving Gases Ø 2 mol 3 mol Ø 2(122. 6 g) 2(74. 6 g) 3(32 g) 3 moles of oxygen equal to 3(22. 4 L) or 67. 2 L at STP 110
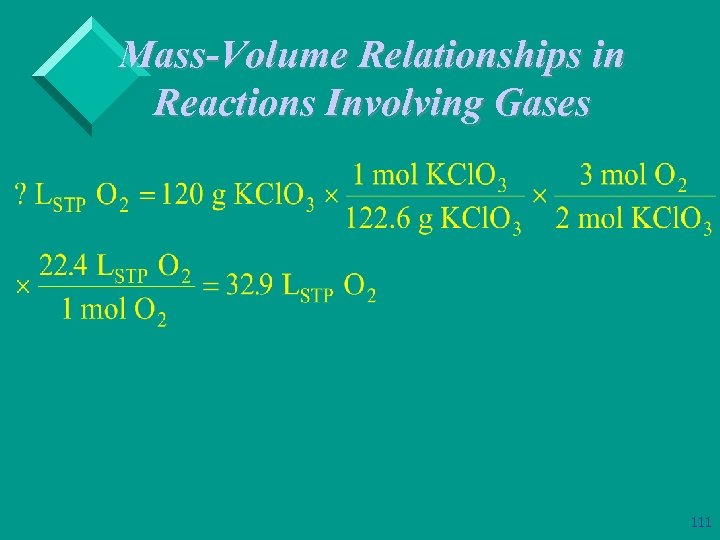 Mass-Volume Relationships in Reactions Involving Gases 111
Mass-Volume Relationships in Reactions Involving Gases 111
 Synthesis Question Ø The lethal dose for hydrogen sulfide is 6 ppm. In other words, if in 1 million molecules of air there are six hydrogen sulfide molecules then that air would be deadly to breathe. How many hydrogen sulfide molecules would be required to reach the lethal dose in a room that is 77 feet long, 62 feet wide and 50 feet tall at 1. 0 atm and 25. 0 o C? 112
Synthesis Question Ø The lethal dose for hydrogen sulfide is 6 ppm. In other words, if in 1 million molecules of air there are six hydrogen sulfide molecules then that air would be deadly to breathe. How many hydrogen sulfide molecules would be required to reach the lethal dose in a room that is 77 feet long, 62 feet wide and 50 feet tall at 1. 0 atm and 25. 0 o C? 112
 Synthesis Question 113
Synthesis Question 113
 Synthesis Question 114
Synthesis Question 114
 Group Question Ø Tires on a car are typically filled to a pressure of 35 psi at 300 K. A tire is 16 inches in radius and 8. 0 inches in thickness. The wheel that the tire is mounted on is 6. 0 inches in radius. What is the mass of the air in a tire? 115
Group Question Ø Tires on a car are typically filled to a pressure of 35 psi at 300 K. A tire is 16 inches in radius and 8. 0 inches in thickness. The wheel that the tire is mounted on is 6. 0 inches in radius. What is the mass of the air in a tire? 115


