7994ecb31055b1ef32b7f76387a879f9.ppt
- Количество слайдов: 91
 Chapter 5 – Force and Motion I I. Newton’s first law. II. Newton’s second law. III. Particular forces: - Gravitational - Weight - Normal - Friction - Tension IV. Newton’s third law.
Chapter 5 – Force and Motion I I. Newton’s first law. II. Newton’s second law. III. Particular forces: - Gravitational - Weight - Normal - Friction - Tension IV. Newton’s third law.
 Force • Forces are what cause any change in the velocity of an object – A force is that which causes an acceleration • The net force is the vector sum of all the forces acting on an object – Also called total force, resultant force, or unbalanced force
Force • Forces are what cause any change in the velocity of an object – A force is that which causes an acceleration • The net force is the vector sum of all the forces acting on an object – Also called total force, resultant force, or unbalanced force
 Zero Net Force • When the net force is equal to zero: – The acceleration is equal to zero – The velocity is constant • Equilibrium occurs when the net force is equal to zero – The object, if at rest, will remain at rest – If the object is moving, it will continue to move at a constant velocity
Zero Net Force • When the net force is equal to zero: – The acceleration is equal to zero – The velocity is constant • Equilibrium occurs when the net force is equal to zero – The object, if at rest, will remain at rest – If the object is moving, it will continue to move at a constant velocity
 Classes of Forces • Contact forces involve physical contact between two objects • Field forces act through empty space – No physical contact is required
Classes of Forces • Contact forces involve physical contact between two objects • Field forces act through empty space – No physical contact is required
 Fundamental Forces • Gravitational force – Between two objects • Electromagnetic forces – Between two charges • Nuclear (strong) force – Between subatomic particles • Weak forces – Arise in certain radioactive decay processes
Fundamental Forces • Gravitational force – Between two objects • Electromagnetic forces – Between two charges • Nuclear (strong) force – Between subatomic particles • Weak forces – Arise in certain radioactive decay processes
 • A spring can be used to calibrate the magnitude of a force • Forces are vectors, so you must use the rules for vector addition to find the net force acting on an object
• A spring can be used to calibrate the magnitude of a force • Forces are vectors, so you must use the rules for vector addition to find the net force acting on an object
 Newton mechanics laws cannot be applied when: 1) The speed of the interacting bodies are a fraction of the speed of light Einstein’s special theory of relativity. 2) The interacting bodies are on the scale of the atomic structure Quantum mechanics I. Newton’s first law: If no net force acts on a body, then the body’s velocity cannot change; the body cannot accelerate v = constant in magnitude and direction. Principle of superposition: when two or more forces act on a body, the net force can be obtained by adding the individual forces as vectors.
Newton mechanics laws cannot be applied when: 1) The speed of the interacting bodies are a fraction of the speed of light Einstein’s special theory of relativity. 2) The interacting bodies are on the scale of the atomic structure Quantum mechanics I. Newton’s first law: If no net force acts on a body, then the body’s velocity cannot change; the body cannot accelerate v = constant in magnitude and direction. Principle of superposition: when two or more forces act on a body, the net force can be obtained by adding the individual forces as vectors.
 Newton’s First Law • If an object does not interact with other objects, it is possible to identify a reference frame in which the object has zero acceleration – This is also called the law of inertia – It defines a special set of reference frames called inertial frames, • We call this an inertial frame of reference Inertial reference frame: where Newton’s laws hold.
Newton’s First Law • If an object does not interact with other objects, it is possible to identify a reference frame in which the object has zero acceleration – This is also called the law of inertia – It defines a special set of reference frames called inertial frames, • We call this an inertial frame of reference Inertial reference frame: where Newton’s laws hold.
 Inertial Frames • Any reference frame that moves with constant velocity relative to an inertial frame is itself an inertial frame • A reference frame that moves with constant velocity relative to the distant stars is the best approximation of an inertial frame – We can consider the Earth to be such an inertial frame although it has a small centripetal acceleration associated with its motion
Inertial Frames • Any reference frame that moves with constant velocity relative to an inertial frame is itself an inertial frame • A reference frame that moves with constant velocity relative to the distant stars is the best approximation of an inertial frame – We can consider the Earth to be such an inertial frame although it has a small centripetal acceleration associated with its motion
 Newton’s First Law – Alternative Statement • In the absence of external forces, when viewed from an inertial reference frame, an object at rest remains at rest and an object in motion continues in motion with a constant velocity – Newton’s First Law describes what happens in the absence of a force – Also tells us that when no force acts on an object, the acceleration of the object is zero
Newton’s First Law – Alternative Statement • In the absence of external forces, when viewed from an inertial reference frame, an object at rest remains at rest and an object in motion continues in motion with a constant velocity – Newton’s First Law describes what happens in the absence of a force – Also tells us that when no force acts on an object, the acceleration of the object is zero
 Inertia and Mass • The tendency of an object to resist any attempt to change its velocity is called inertia • Mass is that property of an object that specifies how much resistance an object exhibits to changes in its velocity
Inertia and Mass • The tendency of an object to resist any attempt to change its velocity is called inertia • Mass is that property of an object that specifies how much resistance an object exhibits to changes in its velocity
 • Mass is an inherent property of an object • Mass is independent of the object’s surroundings • Mass is independent of the method used to measure it • Mass is a scalar quantity • The SI unit of mass is kg
• Mass is an inherent property of an object • Mass is independent of the object’s surroundings • Mass is independent of the method used to measure it • Mass is a scalar quantity • The SI unit of mass is kg
 Mass vs. Weight • Mass and weight are two different quantities • Weight is equal to the magnitude of the gravitational force exerted on the object – Weight will vary with location
Mass vs. Weight • Mass and weight are two different quantities • Weight is equal to the magnitude of the gravitational force exerted on the object – Weight will vary with location
 Newton’s Second Law • When viewed from an inertial frame, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass – Force is the cause of change in motion, as measured by the acceleration • Algebraically, F = m a
Newton’s Second Law • When viewed from an inertial frame, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass – Force is the cause of change in motion, as measured by the acceleration • Algebraically, F = m a
 II. Newton’s second law: The net force on a body is equal to the product of the body’s mass and its acceleration. The acceleration component along a given axis is caused only by the sum of the force components along the same axis, and not by force components along any other axis.
II. Newton’s second law: The net force on a body is equal to the product of the body’s mass and its acceleration. The acceleration component along a given axis is caused only by the sum of the force components along the same axis, and not by force components along any other axis.
 Units of Force
Units of Force
 System: collection of bodies. External force: any force on the bodies inside the system. III. Particular forces: Gravitational: pull directed towards a second body, normally the Earth Weight: magnitude of the upward force needed to balance the gravitational force on the body due to an astronomical body
System: collection of bodies. External force: any force on the bodies inside the system. III. Particular forces: Gravitational: pull directed towards a second body, normally the Earth Weight: magnitude of the upward force needed to balance the gravitational force on the body due to an astronomical body
 Normal force: perpendicular force on a body from a surface against which the body presses. Frictional force: force on a body when the body attempts to slide along a surface. It is parallel to the surface and opposite to the motion.
Normal force: perpendicular force on a body from a surface against which the body presses. Frictional force: force on a body when the body attempts to slide along a surface. It is parallel to the surface and opposite to the motion.
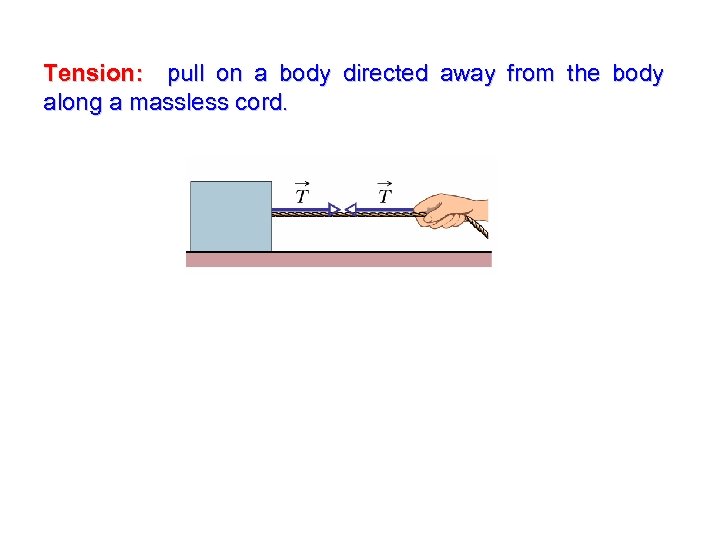 Tension: pull on a body directed away from the body along a massless cord.
Tension: pull on a body directed away from the body along a massless cord.
 Newton’s Third Law • If two objects interact, the force F 12 exerted by object 1 on object 2 is equal in magnitude and opposite in direction to the force F 21 exerted by object 2 on object 1 • F 12 = - F 21 – Note on notation: FAB is the force exerted by A on B
Newton’s Third Law • If two objects interact, the force F 12 exerted by object 1 on object 2 is equal in magnitude and opposite in direction to the force F 21 exerted by object 2 on object 1 • F 12 = - F 21 – Note on notation: FAB is the force exerted by A on B
 Newton’s Third Law, Alternative Statements • • • Forces always occur in pairs A single isolated force cannot exist The action force is equal in magnitude to the reaction force and opposite in direction – One of the forces is the action force, the other is the reaction force – It doesn’t matter which is considered the action and which the reaction – The action and reaction forces must act on different objects and be of the same type
Newton’s Third Law, Alternative Statements • • • Forces always occur in pairs A single isolated force cannot exist The action force is equal in magnitude to the reaction force and opposite in direction – One of the forces is the action force, the other is the reaction force – It doesn’t matter which is considered the action and which the reaction – The action and reaction forces must act on different objects and be of the same type
 Action-Reaction Examples • The force F 12 exerted by object 1 on object 2 is equal in magnitude and opposite in direction to F 21 exerted by object 2 on object 1 • F 12 = - F 21
Action-Reaction Examples • The force F 12 exerted by object 1 on object 2 is equal in magnitude and opposite in direction to F 21 exerted by object 2 on object 1 • F 12 = - F 21
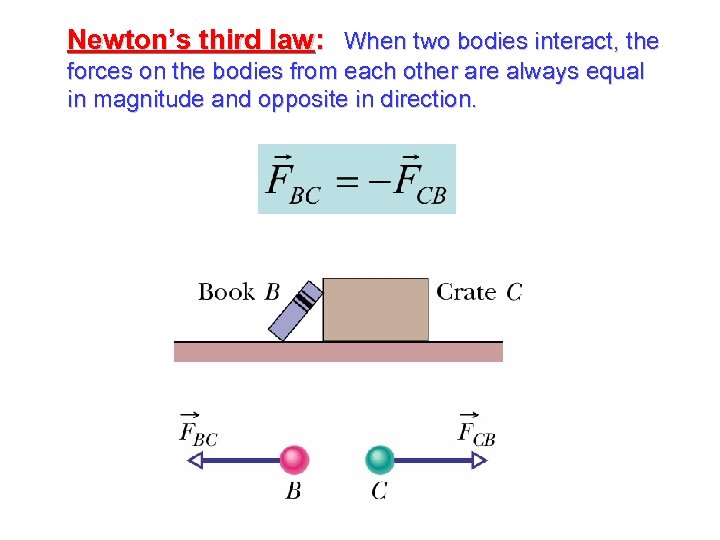 Newton’s third law: When two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction.
Newton’s third law: When two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction.
 QUESTIONS Q 2. Two horizontal forces, pull a banana split across a frictionless counter. Without using a calculator, determine which of the vectors in the free body diagram below best represent: a) F 1, F 2; b) What is the net force component along (c) the x-axis, (d) the y-axis? Into which quadrant do (e) the net-force vector and (f) the split’s acceleration vector point?
QUESTIONS Q 2. Two horizontal forces, pull a banana split across a frictionless counter. Without using a calculator, determine which of the vectors in the free body diagram below best represent: a) F 1, F 2; b) What is the net force component along (c) the x-axis, (d) the y-axis? Into which quadrant do (e) the net-force vector and (f) the split’s acceleration vector point?
 QUESTIONS Q 2. Two horizontal forces, pull a banana split across a frictionless counter. Without using a calculator, determine which of the vectors in the free body diagram below best represent: a) F 1, F 2; b) What is the net force component along (c) the x-axis, (d) the y-axis? Into which quadrant do (e) the net-force vector and (f) the split’s acceleration vector point? Same quadrant, 4
QUESTIONS Q 2. Two horizontal forces, pull a banana split across a frictionless counter. Without using a calculator, determine which of the vectors in the free body diagram below best represent: a) F 1, F 2; b) What is the net force component along (c) the x-axis, (d) the y-axis? Into which quadrant do (e) the net-force vector and (f) the split’s acceleration vector point? Same quadrant, 4
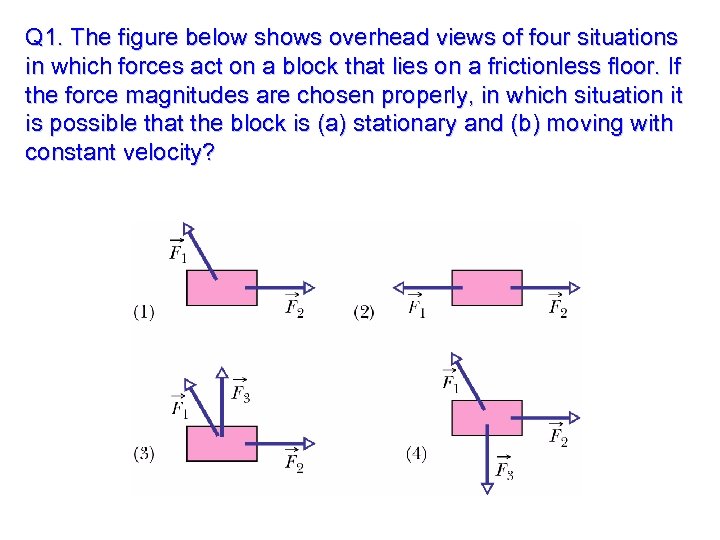 Q 1. The figure below shows overhead views of four situations in which forces act on a block that lies on a frictionless floor. If the force magnitudes are chosen properly, in which situation it is possible that the block is (a) stationary and (b) moving with constant velocity?
Q 1. The figure below shows overhead views of four situations in which forces act on a block that lies on a frictionless floor. If the force magnitudes are chosen properly, in which situation it is possible that the block is (a) stationary and (b) moving with constant velocity?
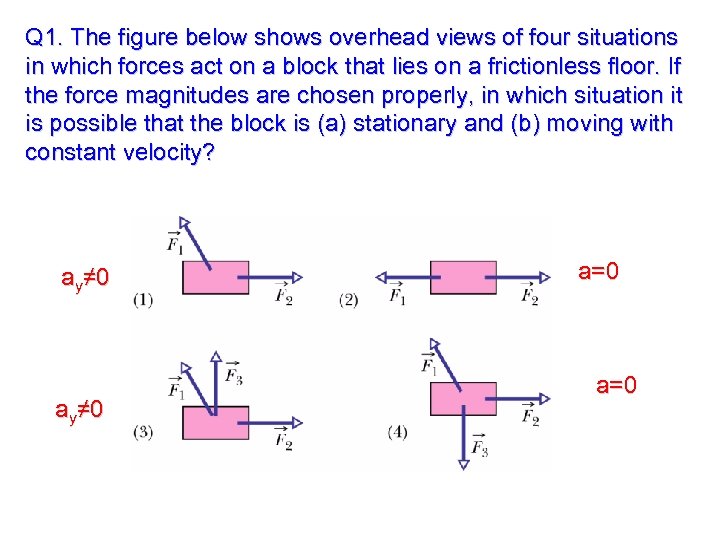 Q 1. The figure below shows overhead views of four situations in which forces act on a block that lies on a frictionless floor. If the force magnitudes are chosen properly, in which situation it is possible that the block is (a) stationary and (b) moving with constant velocity? ay≠ 0 a=0
Q 1. The figure below shows overhead views of four situations in which forces act on a block that lies on a frictionless floor. If the force magnitudes are chosen properly, in which situation it is possible that the block is (a) stationary and (b) moving with constant velocity? ay≠ 0 a=0
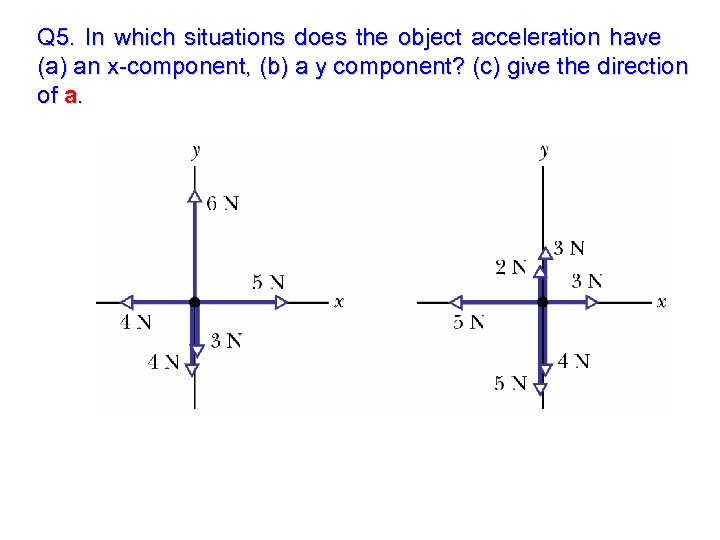 Q 5. In which situations does the object acceleration have (a) an x-component, (b) a y component? (c) give the direction of a.
Q 5. In which situations does the object acceleration have (a) an x-component, (b) a y component? (c) give the direction of a.
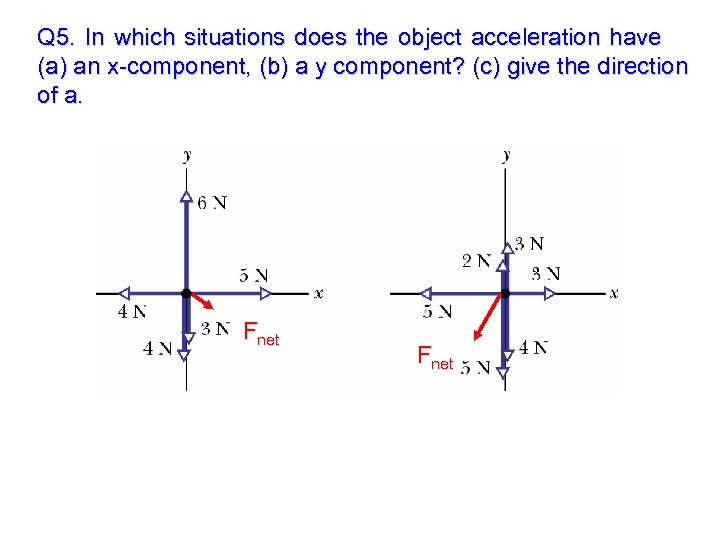 Q 5. In which situations does the object acceleration have (a) an x-component, (b) a y component? (c) give the direction of a. Fnet
Q 5. In which situations does the object acceleration have (a) an x-component, (b) a y component? (c) give the direction of a. Fnet
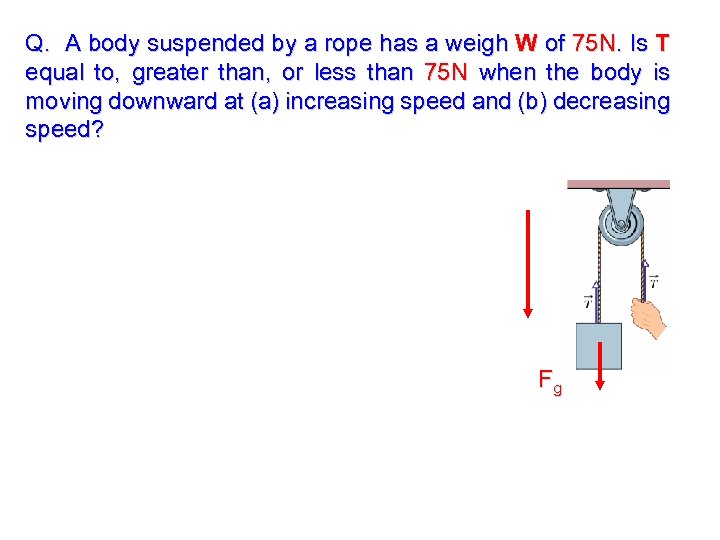 Q. A body suspended by a rope has a weigh W of 75 N. Is T equal to, greater than, or less than 75 N when the body is moving downward at (a) increasing speed and (b) decreasing speed? Fg
Q. A body suspended by a rope has a weigh W of 75 N. Is T equal to, greater than, or less than 75 N when the body is moving downward at (a) increasing speed and (b) decreasing speed? Fg
 Q. A body suspended by a rope has a weigh W of 75 N. Is T equal to, greater than, or less than 75 N when the body is moving downward at (a) increasing speed and (b) decreasing speed? (a) Increasing speed: vf >v 0 a>0 T < Fg (b) Decreasing speed: vf < v 0 a<0 T > Fg Fg
Q. A body suspended by a rope has a weigh W of 75 N. Is T equal to, greater than, or less than 75 N when the body is moving downward at (a) increasing speed and (b) decreasing speed? (a) Increasing speed: vf >v 0 a>0 T < Fg (b) Decreasing speed: vf < v 0 a<0 T > Fg Fg
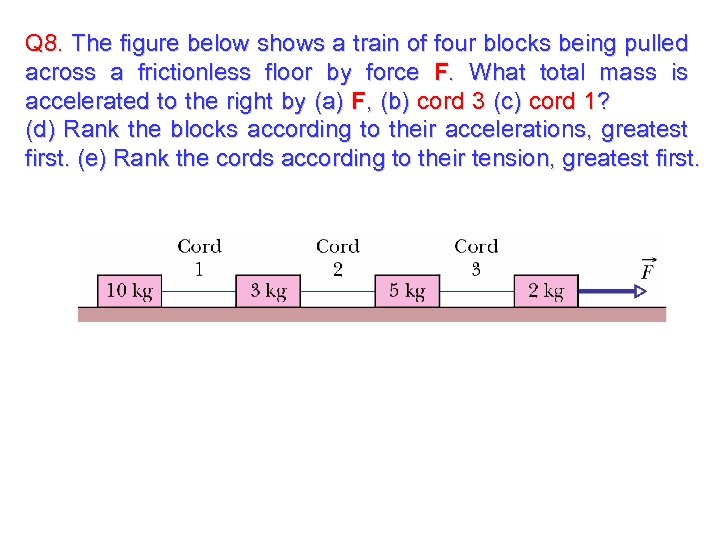 Q 8. The figure below shows a train of four blocks being pulled across a frictionless floor by force F. What total mass is accelerated to the right by (a) F, (b) cord 3 (c) cord 1? (d) Rank the blocks according to their accelerations, greatest first. (e) Rank the cords according to their tension, greatest first.
Q 8. The figure below shows a train of four blocks being pulled across a frictionless floor by force F. What total mass is accelerated to the right by (a) F, (b) cord 3 (c) cord 1? (d) Rank the blocks according to their accelerations, greatest first. (e) Rank the cords according to their tension, greatest first.
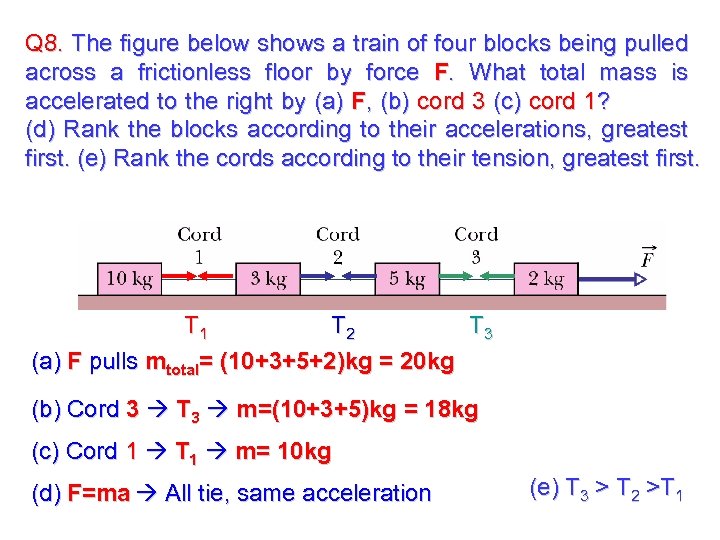 Q 8. The figure below shows a train of four blocks being pulled across a frictionless floor by force F. What total mass is accelerated to the right by (a) F, (b) cord 3 (c) cord 1? (d) Rank the blocks according to their accelerations, greatest first. (e) Rank the cords according to their tension, greatest first. T 2 T 3 T 1 (a) F pulls mtotal= (10+3+5+2)kg = 20 kg (b) Cord 3 T 3 m=(10+3+5)kg = 18 kg (c) Cord 1 T 1 m= 10 kg (d) F=ma All tie, same acceleration (e) T 3 > T 2 >T 1
Q 8. The figure below shows a train of four blocks being pulled across a frictionless floor by force F. What total mass is accelerated to the right by (a) F, (b) cord 3 (c) cord 1? (d) Rank the blocks according to their accelerations, greatest first. (e) Rank the cords according to their tension, greatest first. T 2 T 3 T 1 (a) F pulls mtotal= (10+3+5+2)kg = 20 kg (b) Cord 3 T 3 m=(10+3+5)kg = 18 kg (c) Cord 1 T 1 m= 10 kg (d) F=ma All tie, same acceleration (e) T 3 > T 2 >T 1
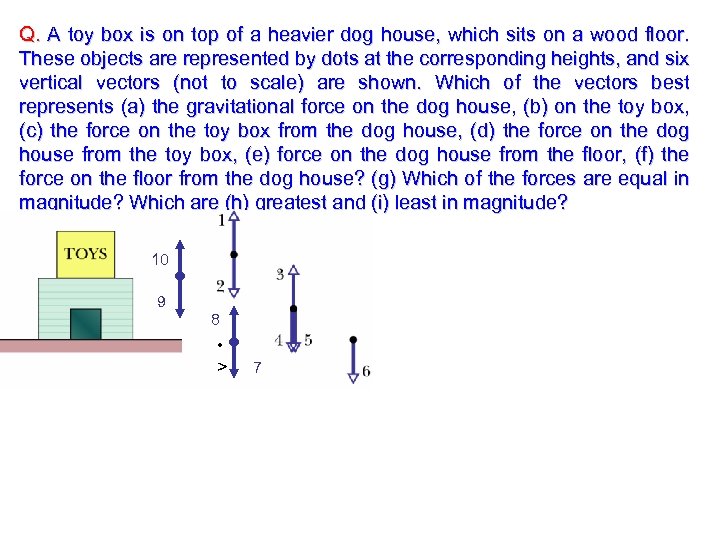 Q. A toy box is on top of a heavier dog house, which sits on a wood floor. These objects are represented by dots at the corresponding heights, and six vertical vectors (not to scale) are shown. Which of the vectors best represents (a) the gravitational force on the dog house, (b) on the toy box, (c) the force on the toy box from the dog house, (d) the force on the dog house from the toy box, (e) force on the dog house from the floor, (f) the force on the floor from the dog house? (g) Which of the forces are equal in magnitude? Which are (h) greatest and (i) least in magnitude? 10 9 8 • > 7
Q. A toy box is on top of a heavier dog house, which sits on a wood floor. These objects are represented by dots at the corresponding heights, and six vertical vectors (not to scale) are shown. Which of the vectors best represents (a) the gravitational force on the dog house, (b) on the toy box, (c) the force on the toy box from the dog house, (d) the force on the dog house from the toy box, (e) force on the dog house from the floor, (f) the force on the floor from the dog house? (g) Which of the forces are equal in magnitude? Which are (h) greatest and (i) least in magnitude? 10 9 8 • > 7
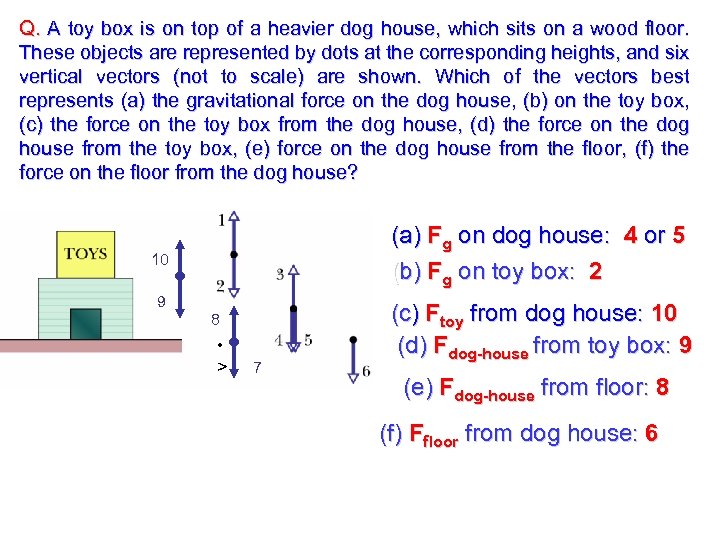 Q. A toy box is on top of a heavier dog house, which sits on a wood floor. These objects are represented by dots at the corresponding heights, and six vertical vectors (not to scale) are shown. Which of the vectors best represents (a) the gravitational force on the dog house, (b) on the toy box, (c) the force on the toy box from the dog house, (d) the force on the dog house from the toy box, (e) force on the dog house from the floor, (f) the force on the floor from the dog house? (a) Fg on dog house: 4 or 5 (b) Fg on toy box: 2 10 9 8 • > 7 (c) Ftoy from dog house: 10 (d) Fdog-house from toy box: 9 (e) Fdog-house from floor: 8 (f) Ffloor from dog house: 6
Q. A toy box is on top of a heavier dog house, which sits on a wood floor. These objects are represented by dots at the corresponding heights, and six vertical vectors (not to scale) are shown. Which of the vectors best represents (a) the gravitational force on the dog house, (b) on the toy box, (c) the force on the toy box from the dog house, (d) the force on the dog house from the toy box, (e) force on the dog house from the floor, (f) the force on the floor from the dog house? (a) Fg on dog house: 4 or 5 (b) Fg on toy box: 2 10 9 8 • > 7 (c) Ftoy from dog house: 10 (d) Fdog-house from toy box: 9 (e) Fdog-house from floor: 8 (f) Ffloor from dog house: 6
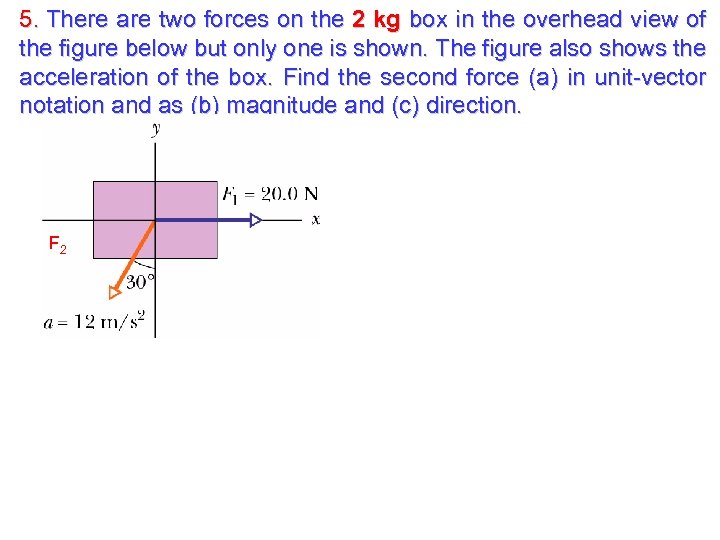 5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
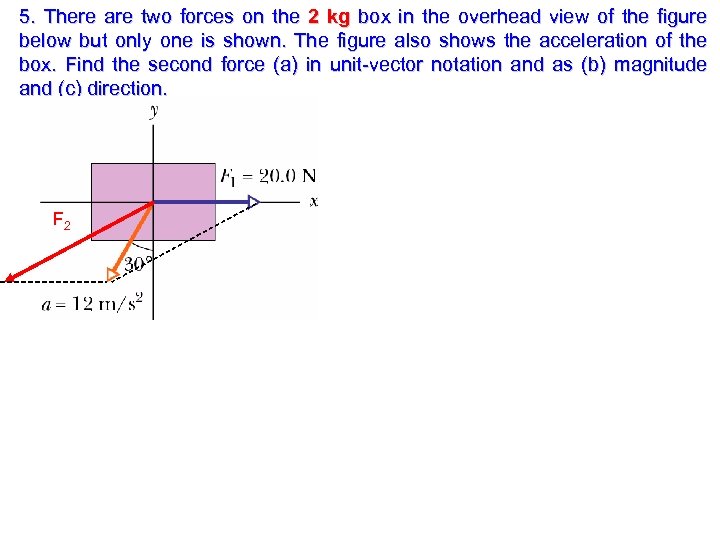 5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
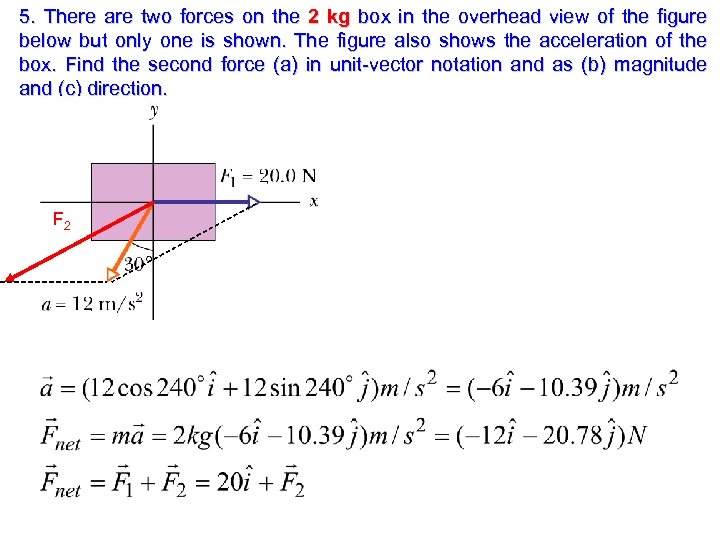 5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
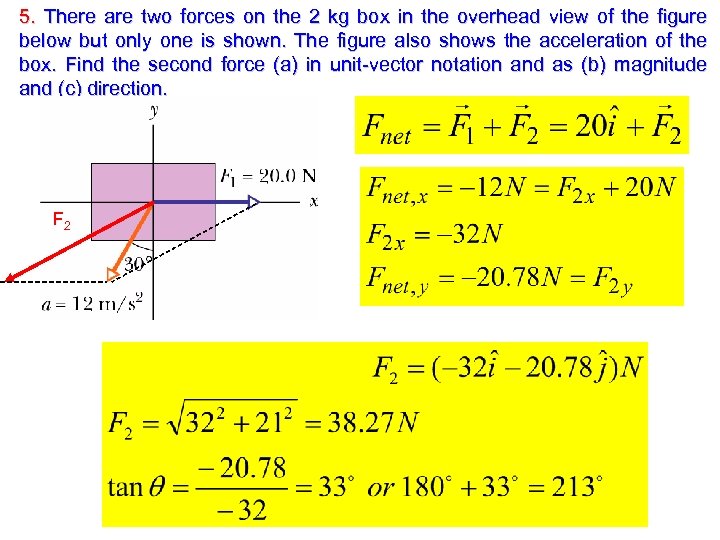 5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
5. There are two forces on the 2 kg box in the overhead view of the figure below but only one is shown. The figure also shows the acceleration of the box. Find the second force (a) in unit-vector notation and as (b) magnitude and (c) direction. F 2
 Rules to solve Dynamic problems - Select a reference system. - Make a drawing of the particle system. - Isolate the particles within the system. - Draw the forces that act on each of the isolated bodies. - Find the components of the forces present. - Apply Newton’s second law (F=ma) to each isolated particle.
Rules to solve Dynamic problems - Select a reference system. - Make a drawing of the particle system. - Isolate the particles within the system. - Draw the forces that act on each of the isolated bodies. - Find the components of the forces present. - Apply Newton’s second law (F=ma) to each isolated particle.
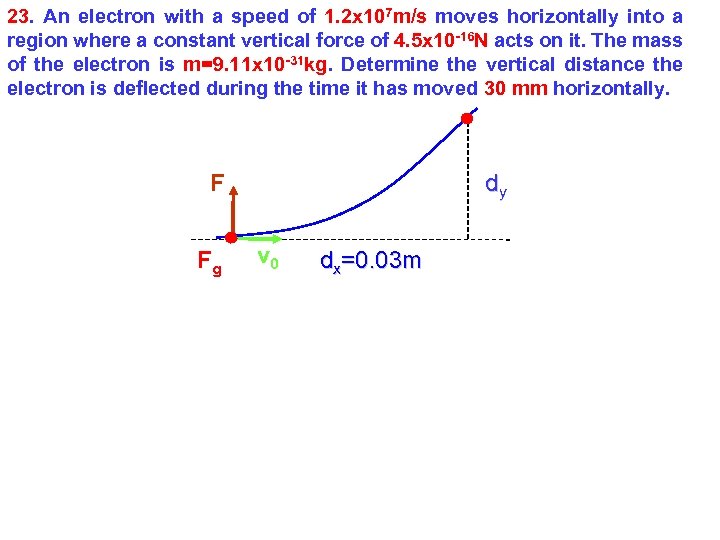 23. An electron with a speed of 1. 2 x 107 m/s moves horizontally into a region where a constant vertical force of 4. 5 x 10 -16 N acts on it. The mass of the electron is m=9. 11 x 10 -31 kg. Determine the vertical distance the electron is deflected during the time it has moved 30 mm horizontally. F Fg dy v 0 dx=0. 03 m
23. An electron with a speed of 1. 2 x 107 m/s moves horizontally into a region where a constant vertical force of 4. 5 x 10 -16 N acts on it. The mass of the electron is m=9. 11 x 10 -31 kg. Determine the vertical distance the electron is deflected during the time it has moved 30 mm horizontally. F Fg dy v 0 dx=0. 03 m
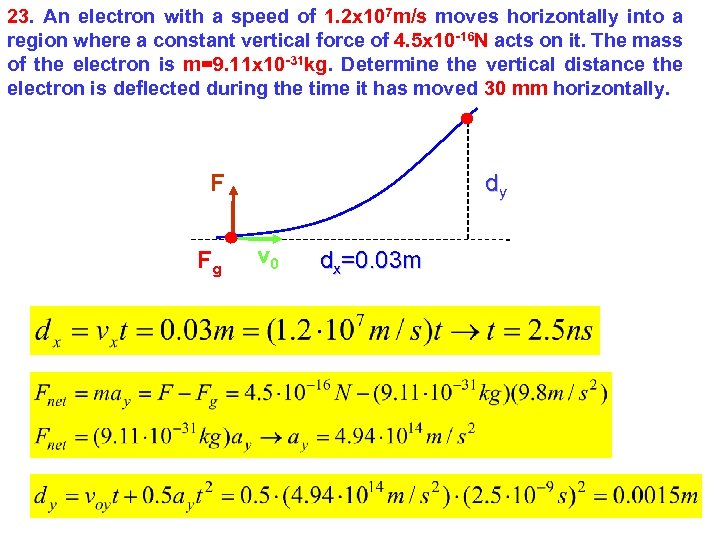 23. An electron with a speed of 1. 2 x 107 m/s moves horizontally into a region where a constant vertical force of 4. 5 x 10 -16 N acts on it. The mass of the electron is m=9. 11 x 10 -31 kg. Determine the vertical distance the electron is deflected during the time it has moved 30 mm horizontally. F Fg dy v 0 dx=0. 03 m
23. An electron with a speed of 1. 2 x 107 m/s moves horizontally into a region where a constant vertical force of 4. 5 x 10 -16 N acts on it. The mass of the electron is m=9. 11 x 10 -31 kg. Determine the vertical distance the electron is deflected during the time it has moved 30 mm horizontally. F Fg dy v 0 dx=0. 03 m
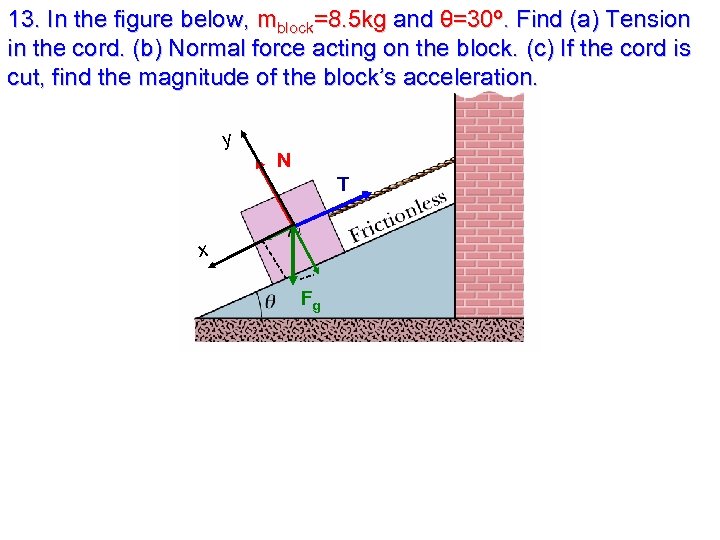 13. In the figure below, mblock=8. 5 kg and θ=30º. Find (a) Tension in the cord. (b) Normal force acting on the block. (c) If the cord is cut, find the magnitude of the block’s acceleration. y N T x Fg
13. In the figure below, mblock=8. 5 kg and θ=30º. Find (a) Tension in the cord. (b) Normal force acting on the block. (c) If the cord is cut, find the magnitude of the block’s acceleration. y N T x Fg
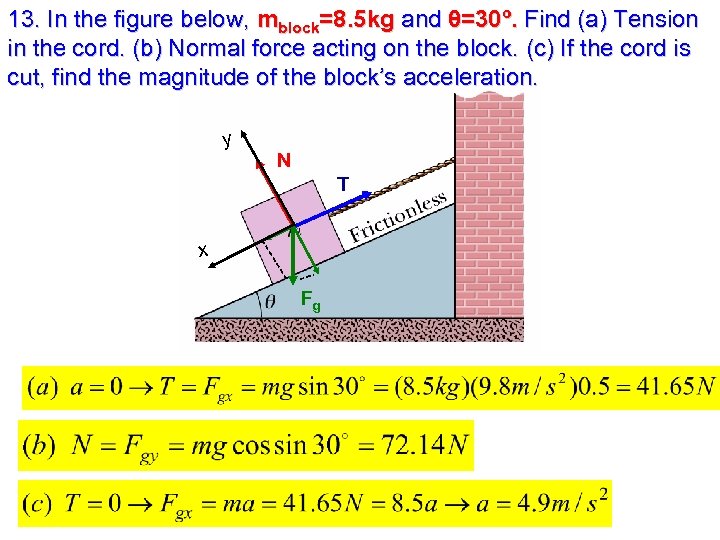 13. In the figure below, mblock=8. 5 kg and θ=30º. Find (a) Tension in the cord. (b) Normal force acting on the block. (c) If the cord is cut, find the magnitude of the block’s acceleration. y N T x Fg
13. In the figure below, mblock=8. 5 kg and θ=30º. Find (a) Tension in the cord. (b) Normal force acting on the block. (c) If the cord is cut, find the magnitude of the block’s acceleration. y N T x Fg
 Friction • Related to microscopic interactions of surfaces • Friction is related to force holding surfaces together • Frictional forces are different depending on whether surfaces are static or moving
Friction • Related to microscopic interactions of surfaces • Friction is related to force holding surfaces together • Frictional forces are different depending on whether surfaces are static or moving
 Kinetic Friction • When a body slides over a surface there is a force exerted by the surface on the body in the opposite direction to the motion of the body • This force is called kinetic friction • The magnitude of the force depends on the nature of the two touching surfaces • For a given pair of surfaces, the magnitude of the kinetic frictional force is proportional to the normal force exerted by the surface on the body.
Kinetic Friction • When a body slides over a surface there is a force exerted by the surface on the body in the opposite direction to the motion of the body • This force is called kinetic friction • The magnitude of the force depends on the nature of the two touching surfaces • For a given pair of surfaces, the magnitude of the kinetic frictional force is proportional to the normal force exerted by the surface on the body.
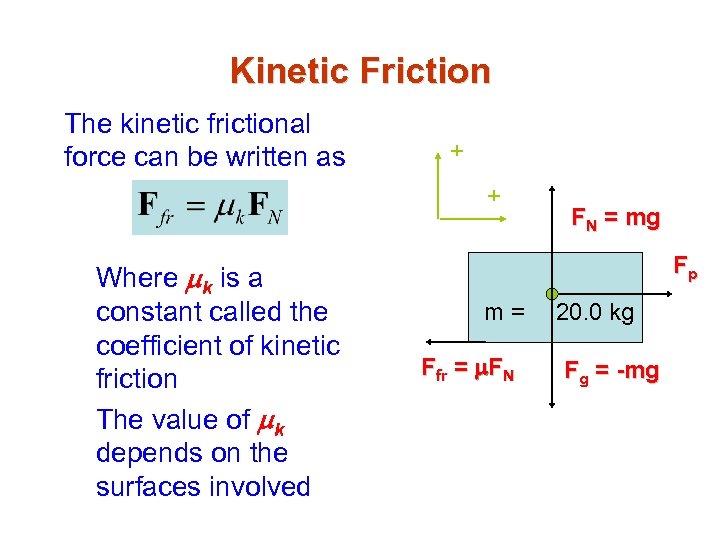 Kinetic Friction The kinetic frictional force can be written as + + Where mk is a constant called the coefficient of kinetic friction The value of mk depends on the surfaces involved FN = mg Fp m= Ffr = m. FN 20. 0 kg Fg = -mg
Kinetic Friction The kinetic frictional force can be written as + + Where mk is a constant called the coefficient of kinetic friction The value of mk depends on the surfaces involved FN = mg Fp m= Ffr = m. FN 20. 0 kg Fg = -mg
 Static Friction A frictional force can arise even if the body remains stationary – A block on the floor - no frictional force FN = -mg m Fg = mg
Static Friction A frictional force can arise even if the body remains stationary – A block on the floor - no frictional force FN = -mg m Fg = mg
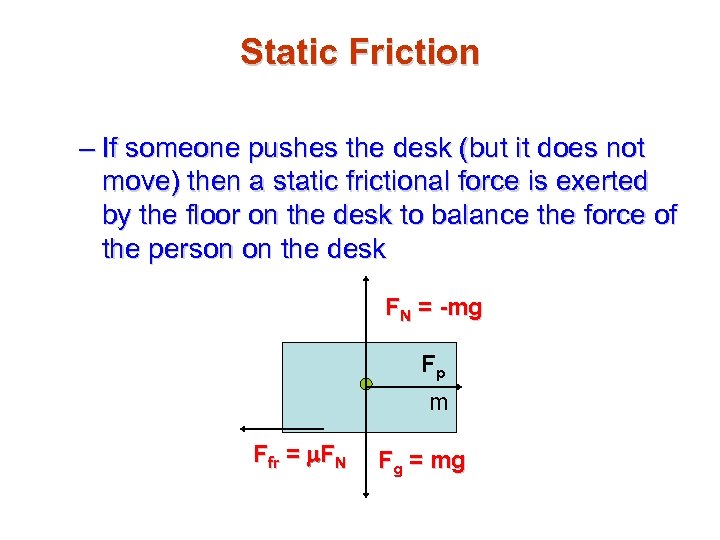 Static Friction – If someone pushes the desk (but it does not move) then a static frictional force is exerted by the floor on the desk to balance the force of the person on the desk FN = -mg Fp m Ffr = m. FN Fg = mg
Static Friction – If someone pushes the desk (but it does not move) then a static frictional force is exerted by the floor on the desk to balance the force of the person on the desk FN = -mg Fp m Ffr = m. FN Fg = mg
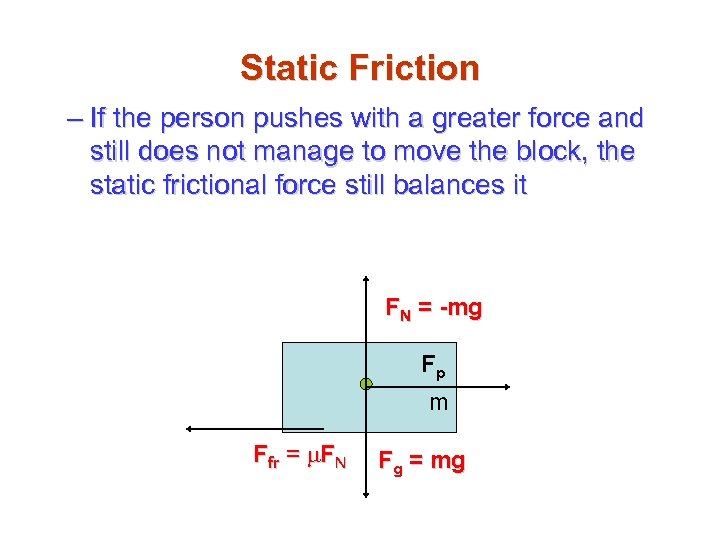 Static Friction – If the person pushes with a greater force and still does not manage to move the block, the static frictional force still balances it FN = -mg Fp m Ffr = m. FN Fg = mg
Static Friction – If the person pushes with a greater force and still does not manage to move the block, the static frictional force still balances it FN = -mg Fp m Ffr = m. FN Fg = mg
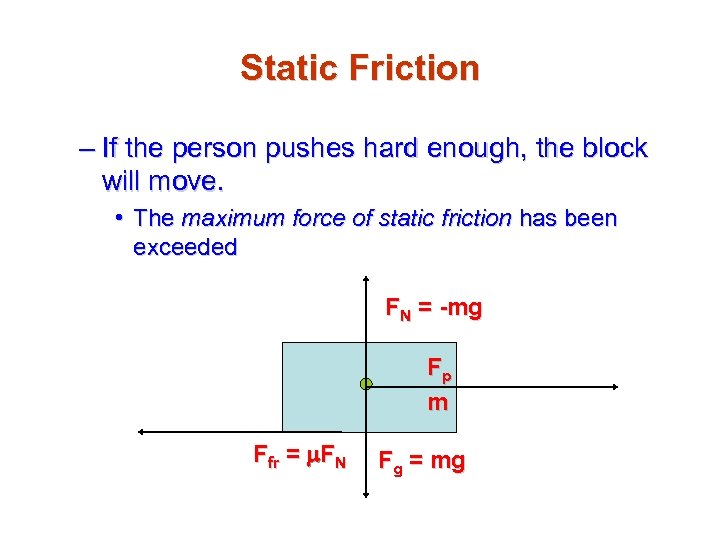 Static Friction – If the person pushes hard enough, the block will move. • The maximum force of static friction has been exceeded FN = -mg Fp m Ffr = m. FN Fg = mg
Static Friction – If the person pushes hard enough, the block will move. • The maximum force of static friction has been exceeded FN = -mg Fp m Ffr = m. FN Fg = mg
 Static Friction • The maximum force of static friction is given by • Static friction can take any value from zero to ms. FN – In other words
Static Friction • The maximum force of static friction is given by • Static friction can take any value from zero to ms. FN – In other words
 Forces on an incline • Often when solving problems involving Newton’s laws we will need to deal with resolving acceleration due to gravity on an inclined surface
Forces on an incline • Often when solving problems involving Newton’s laws we will need to deal with resolving acceleration due to gravity on an inclined surface
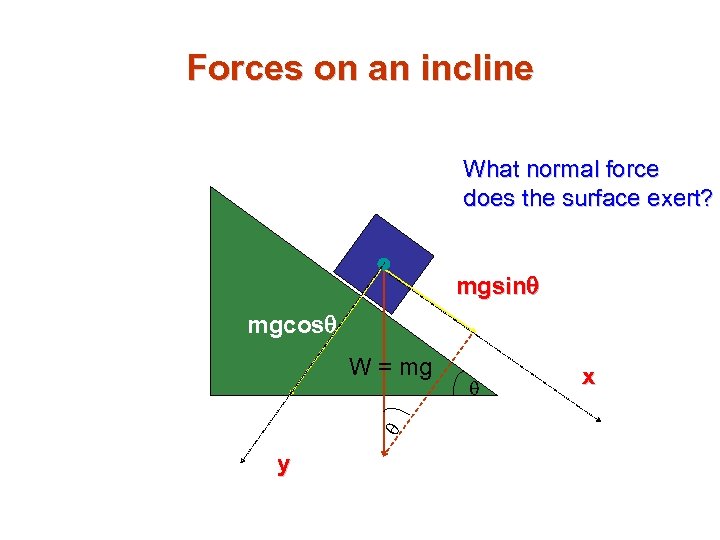 Forces on an incline What normal force does the surface exert? mgsinq mgcosq q W = mg y q x
Forces on an incline What normal force does the surface exert? mgsinq mgcosq q W = mg y q x
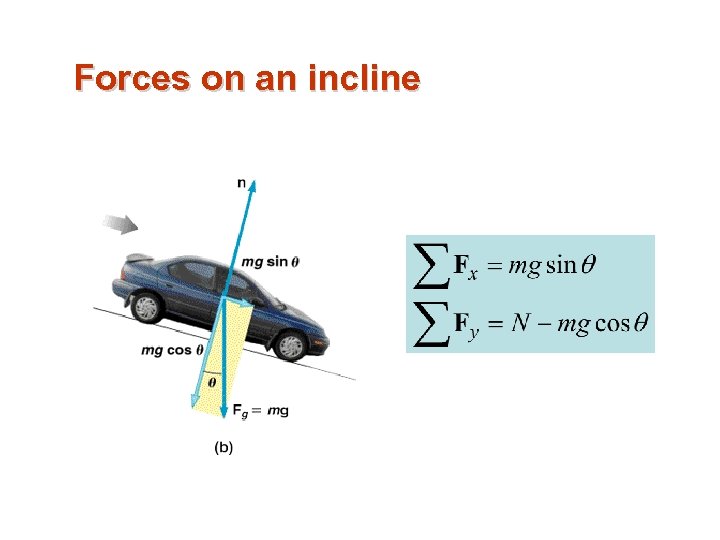 Forces on an incline
Forces on an incline
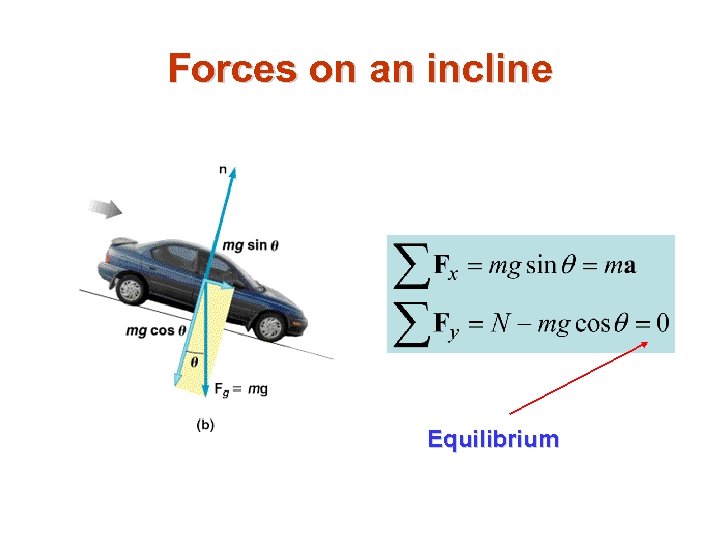 Forces on an incline Equilibrium
Forces on an incline Equilibrium
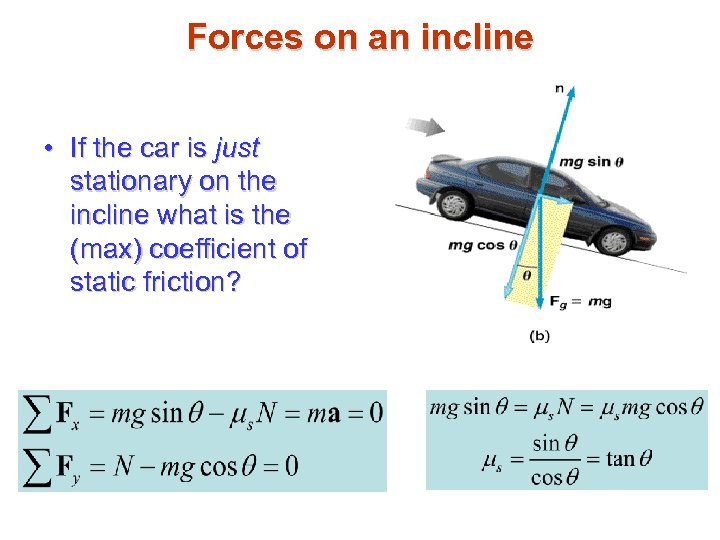 Forces on an incline • If the car is just stationary on the incline what is the (max) coefficient of static friction?
Forces on an incline • If the car is just stationary on the incline what is the (max) coefficient of static friction?
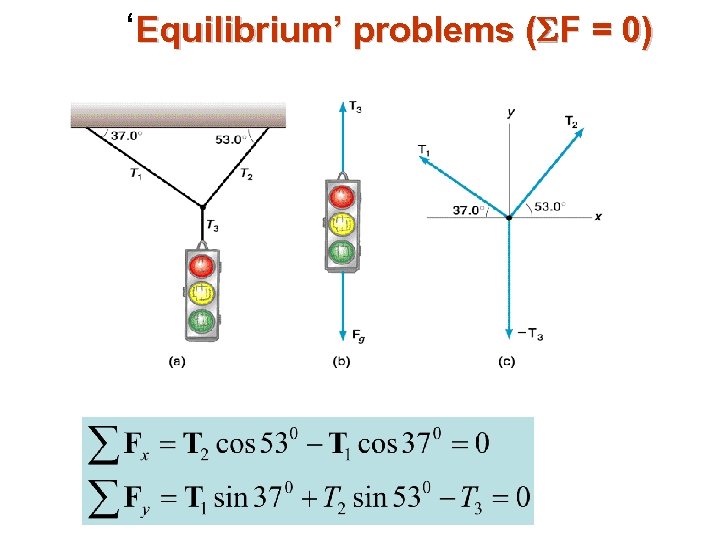 ‘Equilibrium’ problems ( F = 0)
‘Equilibrium’ problems ( F = 0)
 Connected Object problems • One problem often posed is how to work out acceleration of a system of masses connected via strings and/or pulleys – for example - Two blocks are fastened to the ceiling of an elevator.
Connected Object problems • One problem often posed is how to work out acceleration of a system of masses connected via strings and/or pulleys – for example - Two blocks are fastened to the ceiling of an elevator.
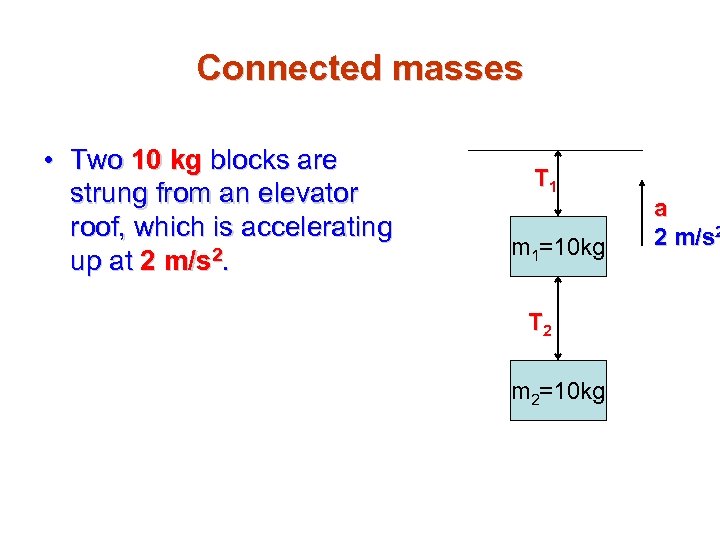 Connected masses • Two 10 kg blocks are strung from an elevator roof, which is accelerating up at 2 m/s 2. T 1 m 1=10 kg T 2 m 2=10 kg a 2 m/s 2
Connected masses • Two 10 kg blocks are strung from an elevator roof, which is accelerating up at 2 m/s 2. T 1 m 1=10 kg T 2 m 2=10 kg a 2 m/s 2
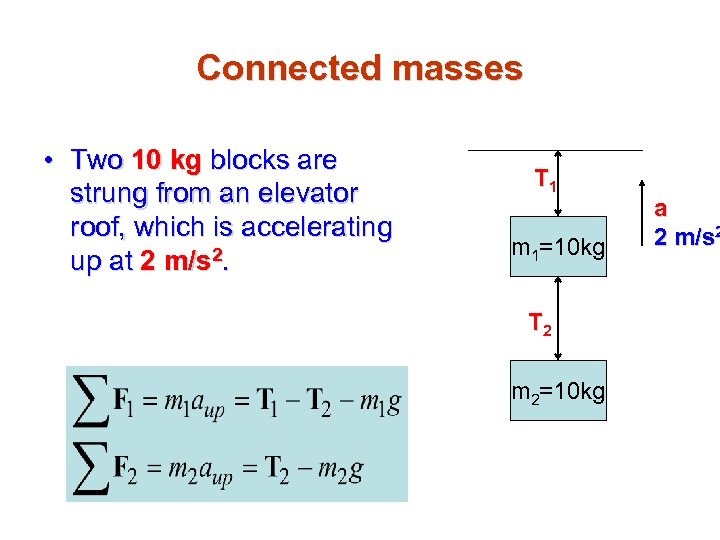 Connected masses • Two 10 kg blocks are strung from an elevator roof, which is accelerating up at 2 m/s 2. T 1 m 1=10 kg T 2 m 2=10 kg a 2 m/s 2
Connected masses • Two 10 kg blocks are strung from an elevator roof, which is accelerating up at 2 m/s 2. T 1 m 1=10 kg T 2 m 2=10 kg a 2 m/s 2
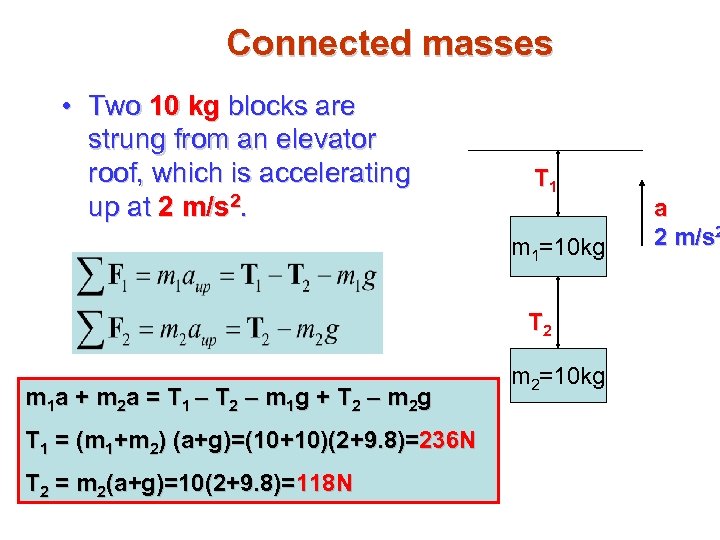 Connected masses • Two 10 kg blocks are strung from an elevator roof, which is accelerating up at 2 m/s 2. T 1 m 1=10 kg T 2 m 1 a + m 2 a = T 1 – T 2 – m 1 g + T 2 – m 2 g T 1 = (m 1+m 2) (a+g)=(10+10)(2+9. 8)=236 N T 2 = m 2(a+g)=10(2+9. 8)=118 N m 2=10 kg a 2 m/s 2
Connected masses • Two 10 kg blocks are strung from an elevator roof, which is accelerating up at 2 m/s 2. T 1 m 1=10 kg T 2 m 1 a + m 2 a = T 1 – T 2 – m 1 g + T 2 – m 2 g T 1 = (m 1+m 2) (a+g)=(10+10)(2+9. 8)=236 N T 2 = m 2(a+g)=10(2+9. 8)=118 N m 2=10 kg a 2 m/s 2
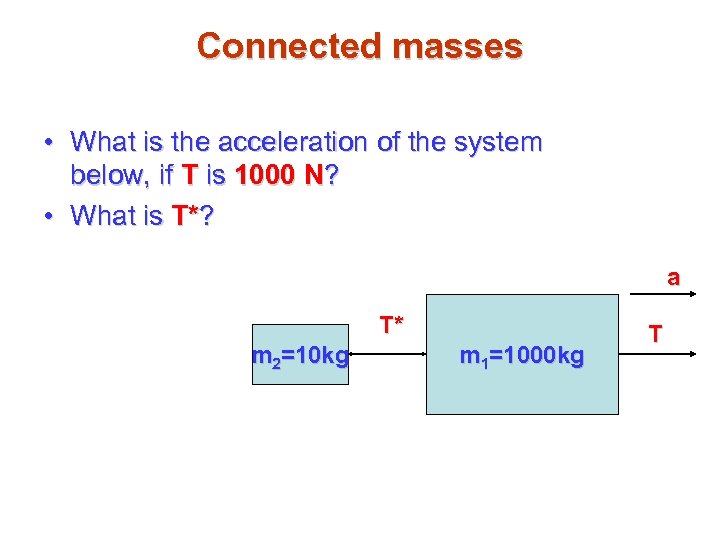 Connected masses • What is the acceleration of the system below, if T is 1000 N? • What is T*? a T* m 2=10 kg m 1=1000 kg T
Connected masses • What is the acceleration of the system below, if T is 1000 N? • What is T*? a T* m 2=10 kg m 1=1000 kg T
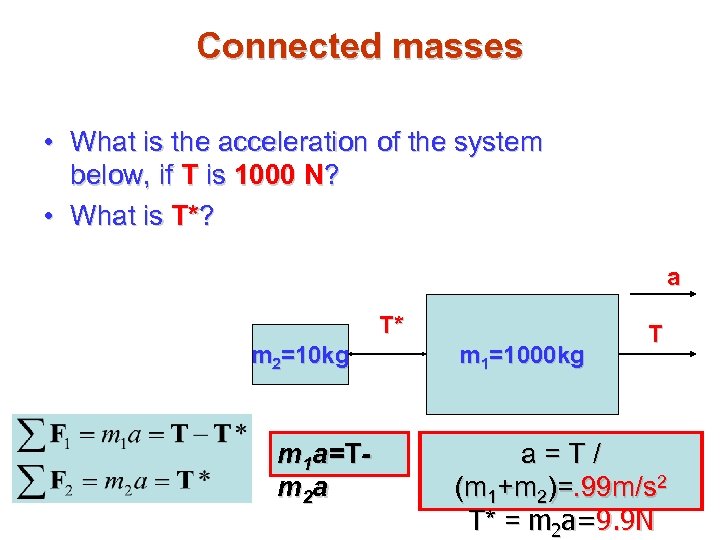 Connected masses • What is the acceleration of the system below, if T is 1000 N? • What is T*? a T* m 2=10 kg m 1 a=Tm 2 a m 1=1000 kg T a=T/ (m 1+m 2)=. 99 m/s 2 T* = m 2 a=9. 9 N
Connected masses • What is the acceleration of the system below, if T is 1000 N? • What is T*? a T* m 2=10 kg m 1 a=Tm 2 a m 1=1000 kg T a=T/ (m 1+m 2)=. 99 m/s 2 T* = m 2 a=9. 9 N
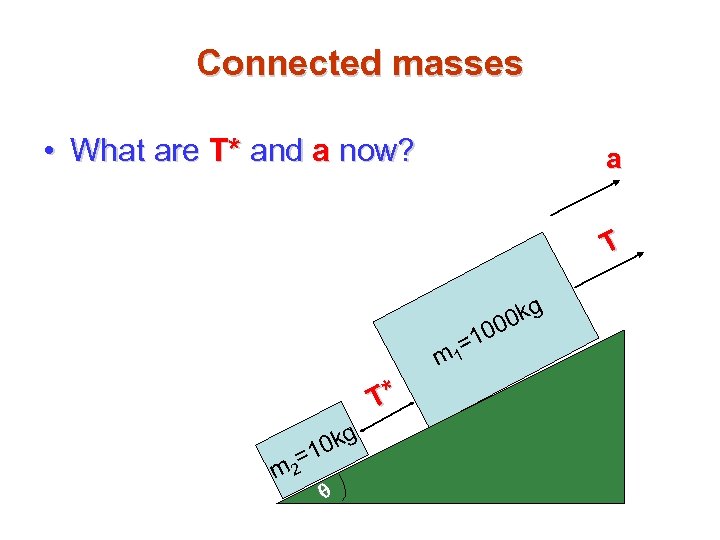 Connected masses • What are T* and a now? a T m T* q q = m 2 0 kg 1 =1 1 0 0 kg 0
Connected masses • What are T* and a now? a T m T* q q = m 2 0 kg 1 =1 1 0 0 kg 0
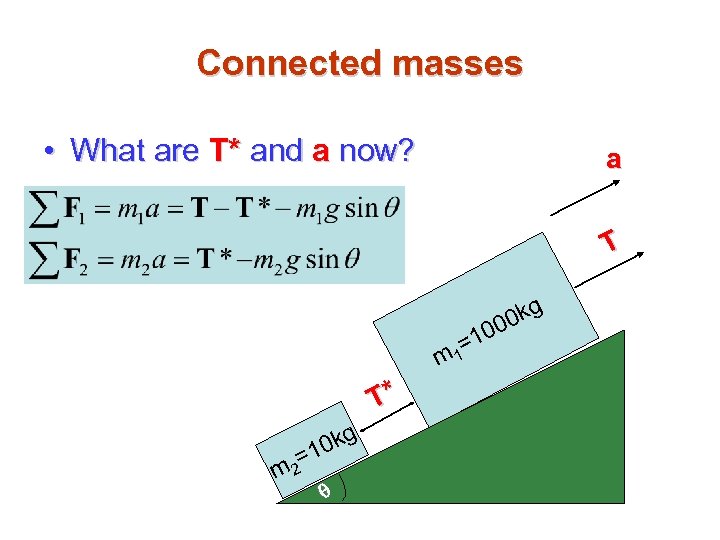 Connected masses • What are T* and a now? a T m T* q q = m 2 0 kg 1 =1 1 0 0 kg 0
Connected masses • What are T* and a now? a T m T* q q = m 2 0 kg 1 =1 1 0 0 kg 0
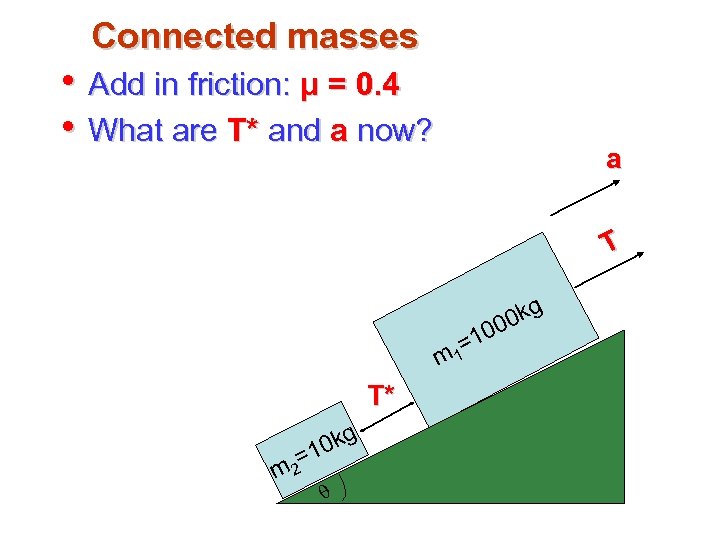 Connected masses • Add in friction: μ = 0. 4 • What are T* and a now? a T m T* q = m 2 0 kg 1 =1 1 0 0 kg 0
Connected masses • Add in friction: μ = 0. 4 • What are T* and a now? a T m T* q = m 2 0 kg 1 =1 1 0 0 kg 0
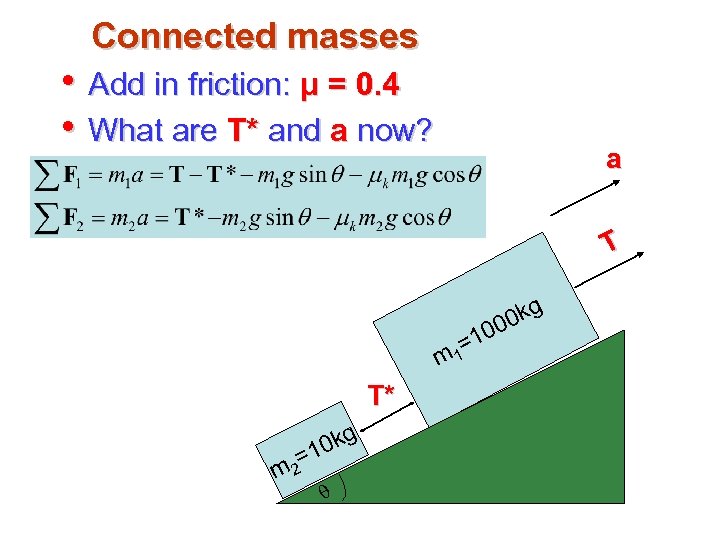 Connected masses • Add in friction: μ = 0. 4 • What are T* and a now? a T m T* q = m 2 0 kg 1 =1 1 0 0 kg 0
Connected masses • Add in friction: μ = 0. 4 • What are T* and a now? a T m T* q = m 2 0 kg 1 =1 1 0 0 kg 0
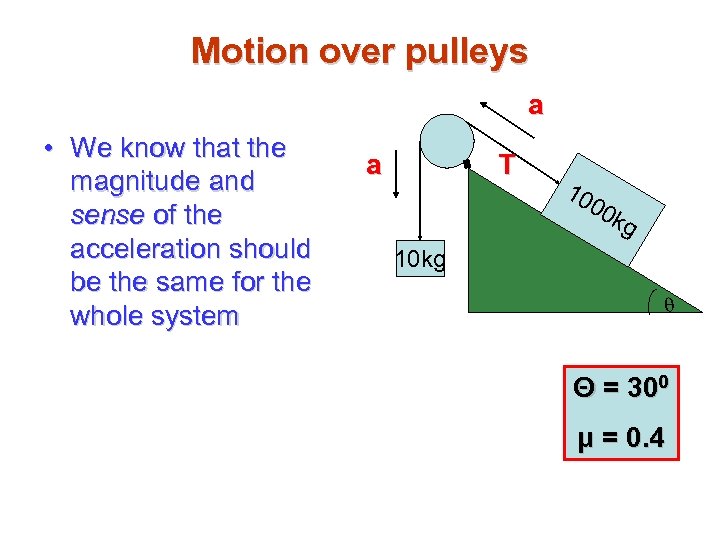 Motion over pulleys a • We know that the magnitude and sense of the acceleration should be the same for the whole system T a 10 00 kg 10 kg q Θ = 300 μ = 0. 4
Motion over pulleys a • We know that the magnitude and sense of the acceleration should be the same for the whole system T a 10 00 kg 10 kg q Θ = 300 μ = 0. 4
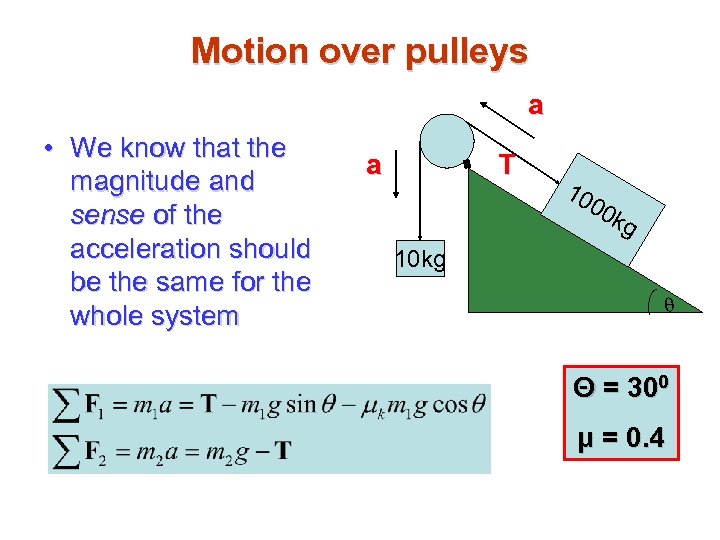 Motion over pulleys a • We know that the magnitude and sense of the acceleration should be the same for the whole system T a 10 00 kg 10 kg q Θ = 300 μ = 0. 4
Motion over pulleys a • We know that the magnitude and sense of the acceleration should be the same for the whole system T a 10 00 kg 10 kg q Θ = 300 μ = 0. 4
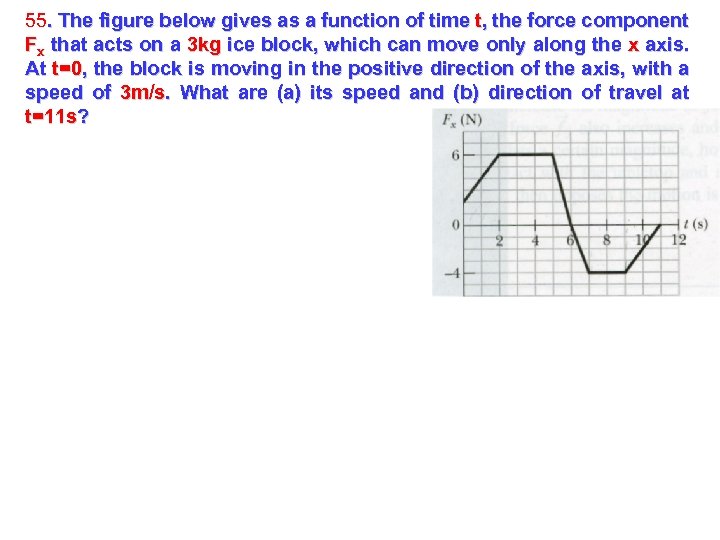 55. The figure below gives as a function of time t, the force component Fx that acts on a 3 kg ice block, which can move only along the x axis. At t=0, the block is moving in the positive direction of the axis, with a speed of 3 m/s. What are (a) its speed and (b) direction of travel at t=11 s?
55. The figure below gives as a function of time t, the force component Fx that acts on a 3 kg ice block, which can move only along the x axis. At t=0, the block is moving in the positive direction of the axis, with a speed of 3 m/s. What are (a) its speed and (b) direction of travel at t=11 s?
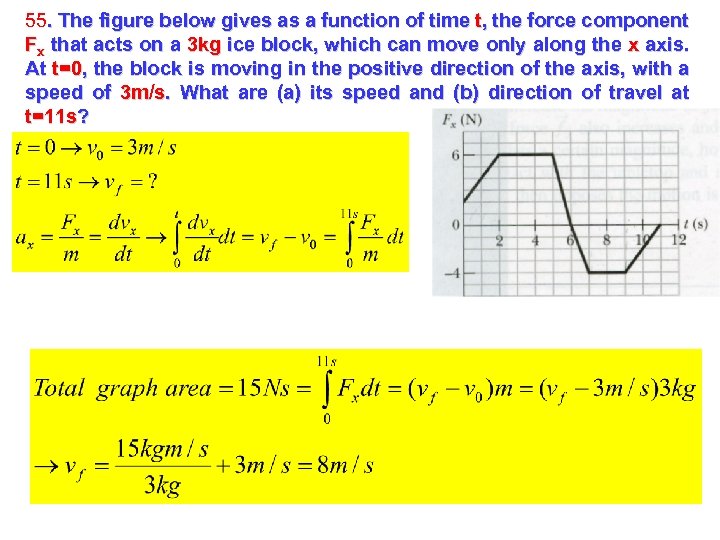 55. The figure below gives as a function of time t, the force component Fx that acts on a 3 kg ice block, which can move only along the x axis. At t=0, the block is moving in the positive direction of the axis, with a speed of 3 m/s. What are (a) its speed and (b) direction of travel at t=11 s?
55. The figure below gives as a function of time t, the force component Fx that acts on a 3 kg ice block, which can move only along the x axis. At t=0, the block is moving in the positive direction of the axis, with a speed of 3 m/s. What are (a) its speed and (b) direction of travel at t=11 s?
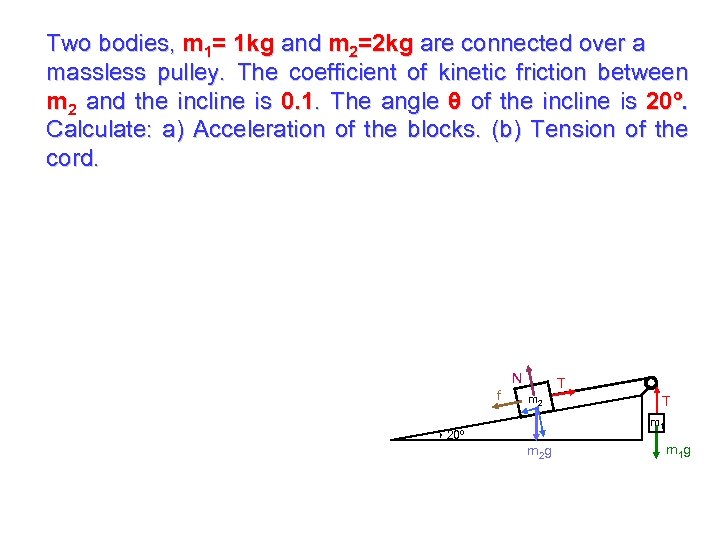 Two bodies, m 1= 1 kg and m 2=2 kg are connected over a massless pulley. The coefficient of kinetic friction between m 2 and the incline is 0. 1. The angle θ of the incline is 20º. Calculate: a) Acceleration of the blocks. (b) Tension of the cord. N f T m 2 T m 1 20º m 2 g m 1 g
Two bodies, m 1= 1 kg and m 2=2 kg are connected over a massless pulley. The coefficient of kinetic friction between m 2 and the incline is 0. 1. The angle θ of the incline is 20º. Calculate: a) Acceleration of the blocks. (b) Tension of the cord. N f T m 2 T m 1 20º m 2 g m 1 g
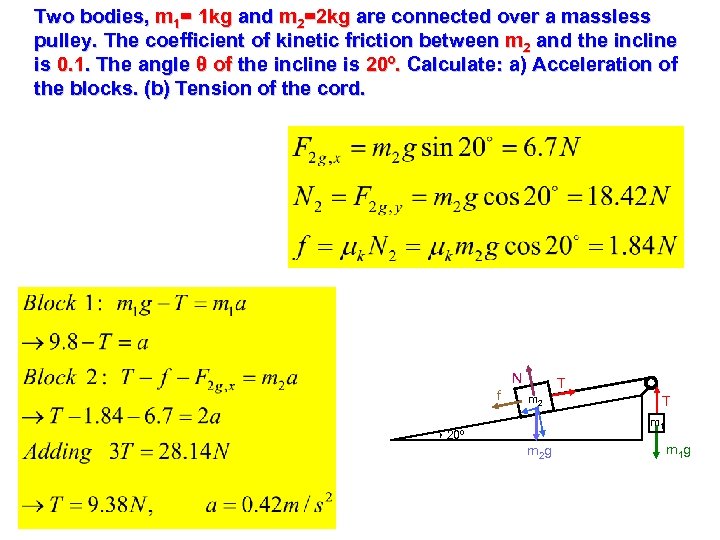 Two bodies, m 1= 1 kg and m 2=2 kg are connected over a massless pulley. The coefficient of kinetic friction between m 2 and the incline is 0. 1. The angle θ of the incline is 20º. Calculate: a) Acceleration of the blocks. (b) Tension of the cord. N f T m 2 T m 1 20º m 2 g m 1 g
Two bodies, m 1= 1 kg and m 2=2 kg are connected over a massless pulley. The coefficient of kinetic friction between m 2 and the incline is 0. 1. The angle θ of the incline is 20º. Calculate: a) Acceleration of the blocks. (b) Tension of the cord. N f T m 2 T m 1 20º m 2 g m 1 g
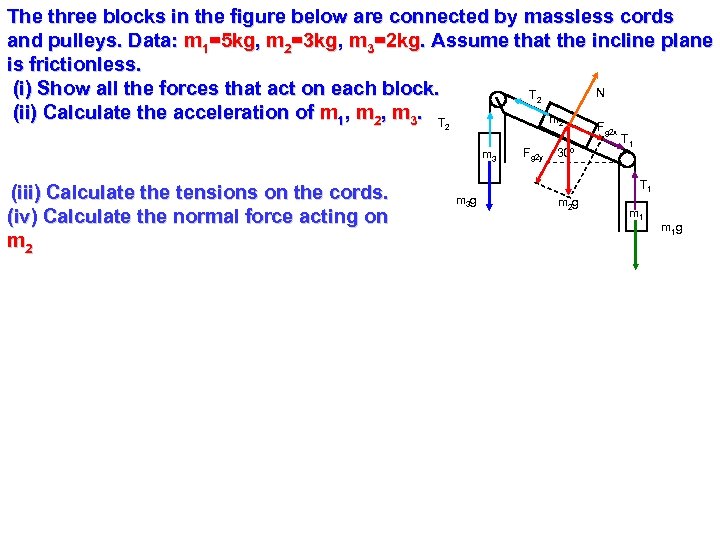 The three blocks in the figure below are connected by massless cords and pulleys. Data: m 1=5 kg, m 2=3 kg, m 3=2 kg. Assume that the incline plane is frictionless. (i) Show all the forces that act on each block. N T (ii) Calculate the acceleration of m 1, m 2, m 3. T m 2 2 2 m 3 (iii) Calculate the tensions on the cords. (iv) Calculate the normal force acting on m 2 m 3 g Fg 2 y 30º Fg 2 x T 1 m 2 g m 1 g
The three blocks in the figure below are connected by massless cords and pulleys. Data: m 1=5 kg, m 2=3 kg, m 3=2 kg. Assume that the incline plane is frictionless. (i) Show all the forces that act on each block. N T (ii) Calculate the acceleration of m 1, m 2, m 3. T m 2 2 2 m 3 (iii) Calculate the tensions on the cords. (iv) Calculate the normal force acting on m 2 m 3 g Fg 2 y 30º Fg 2 x T 1 m 2 g m 1 g
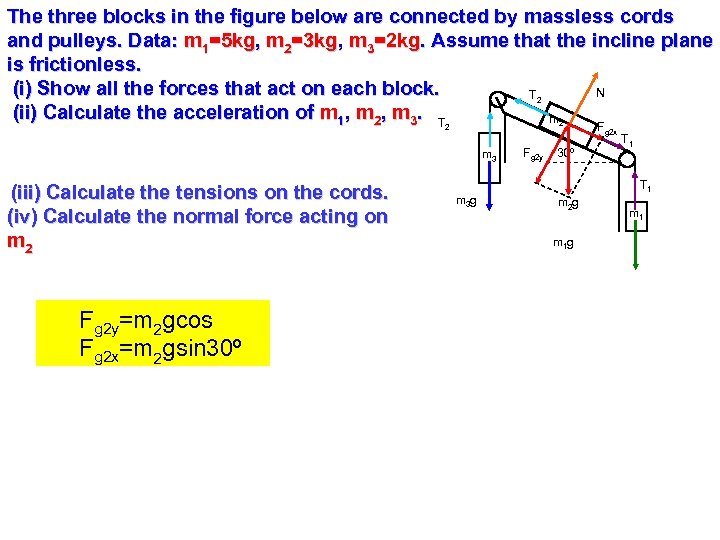 The three blocks in the figure below are connected by massless cords and pulleys. Data: m 1=5 kg, m 2=3 kg, m 3=2 kg. Assume that the incline plane is frictionless. (i) Show all the forces that act on each block. N T (ii) Calculate the acceleration of m 1, m 2, m 3. T m 2 2 2 m 3 (iii) Calculate the tensions on the cords. (iv) Calculate the normal force acting on m 2 Fg 2 y=m 2 gcos Fg 2 x=m 2 gsin 30º m 3 g Fg 2 y 30º Fg 2 x T 1 m 2 g m 1
The three blocks in the figure below are connected by massless cords and pulleys. Data: m 1=5 kg, m 2=3 kg, m 3=2 kg. Assume that the incline plane is frictionless. (i) Show all the forces that act on each block. N T (ii) Calculate the acceleration of m 1, m 2, m 3. T m 2 2 2 m 3 (iii) Calculate the tensions on the cords. (iv) Calculate the normal force acting on m 2 Fg 2 y=m 2 gcos Fg 2 x=m 2 gsin 30º m 3 g Fg 2 y 30º Fg 2 x T 1 m 2 g m 1
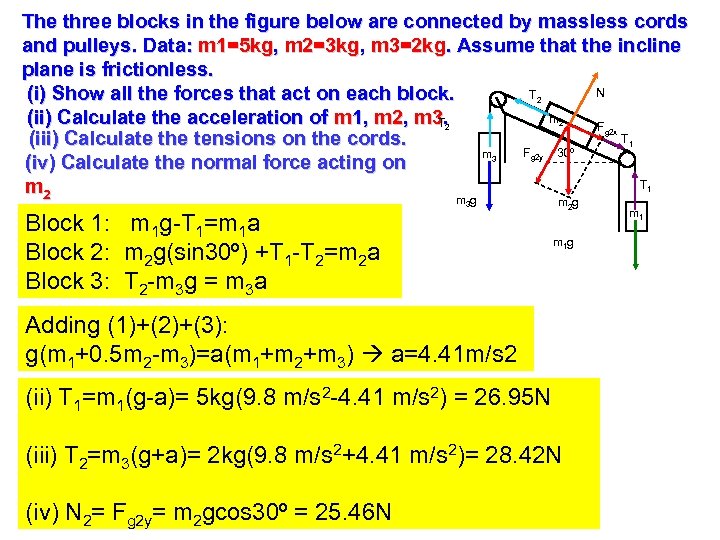 The three blocks in the figure below are connected by massless cords and pulleys. Data: m 1=5 kg, m 2=3 kg, m 3=2 kg. Assume that the incline plane is frictionless. N T (i) Show all the forces that act on each block. m (ii) Calculate the acceleration of m 1, m 2, m 3. T F T (iii) Calculate the tensions on the cords. 30º F m (iv) Calculate the normal force acting on T m 2 mg 2 2 2 g 2 x 1 3 g 2 y 1 3 Block 1: m 1 g-T 1=m 1 a Block 2: m 2 g(sin 30º) +T 1 -T 2=m 2 a Block 3: T 2 -m 3 g = m 3 a m 2 g m 1 g Adding (1)+(2)+(3): g(m 1+0. 5 m 2 -m 3)=a(m 1+m 2+m 3) a=4. 41 m/s 2 (ii) T 1=m 1(g-a)= 5 kg(9. 8 m/s 2 -4. 41 m/s 2) = 26. 95 N (iii) T 2=m 3(g+a)= 2 kg(9. 8 m/s 2+4. 41 m/s 2)= 28. 42 N (iv) N 2= Fg 2 y= m 2 gcos 30º = 25. 46 N m 1
The three blocks in the figure below are connected by massless cords and pulleys. Data: m 1=5 kg, m 2=3 kg, m 3=2 kg. Assume that the incline plane is frictionless. N T (i) Show all the forces that act on each block. m (ii) Calculate the acceleration of m 1, m 2, m 3. T F T (iii) Calculate the tensions on the cords. 30º F m (iv) Calculate the normal force acting on T m 2 mg 2 2 2 g 2 x 1 3 g 2 y 1 3 Block 1: m 1 g-T 1=m 1 a Block 2: m 2 g(sin 30º) +T 1 -T 2=m 2 a Block 3: T 2 -m 3 g = m 3 a m 2 g m 1 g Adding (1)+(2)+(3): g(m 1+0. 5 m 2 -m 3)=a(m 1+m 2+m 3) a=4. 41 m/s 2 (ii) T 1=m 1(g-a)= 5 kg(9. 8 m/s 2 -4. 41 m/s 2) = 26. 95 N (iii) T 2=m 3(g+a)= 2 kg(9. 8 m/s 2+4. 41 m/s 2)= 28. 42 N (iv) N 2= Fg 2 y= m 2 gcos 30º = 25. 46 N m 1
 1 B. (a) What should be the magnitude of F in the figure below if the body of mass m=10 kg is to slide up along a frictionless incline plane with constant y acceleration a=1. 98 m/s 2? (b) What is the magnitude of the Normal force? N x 20º F 30º Fg
1 B. (a) What should be the magnitude of F in the figure below if the body of mass m=10 kg is to slide up along a frictionless incline plane with constant y acceleration a=1. 98 m/s 2? (b) What is the magnitude of the Normal force? N x 20º F 30º Fg
 1 B. (a) What should be the magnitude of F in the figure below if the body of mass m=10 kg is to slide up along a frictionless incline plane with constant y acceleration a=1. 98 m/s 2? (b) What is the magnitude of the Normal force? N x 20º F 30º Fg
1 B. (a) What should be the magnitude of F in the figure below if the body of mass m=10 kg is to slide up along a frictionless incline plane with constant y acceleration a=1. 98 m/s 2? (b) What is the magnitude of the Normal force? N x 20º F 30º Fg
 Three forces, given by , , and , act on an object to give it an acceleration of magnitude 3. 75 m/s 2. (a) What is the direction of the acceleration? (b) What is the mass of the object? (c) If the object is initially at rest, what is its speed after 10. 0 s? (d) What are the velocity components of the object after 10. 0 s?
Three forces, given by , , and , act on an object to give it an acceleration of magnitude 3. 75 m/s 2. (a) What is the direction of the acceleration? (b) What is the mass of the object? (c) If the object is initially at rest, what is its speed after 10. 0 s? (d) What are the velocity components of the object after 10. 0 s?
 Three forces, given by , , and , act on an object to give it an acceleration of magnitude 3. 75 m/s 2. (a) What is the direction of the acceleration? (b) What is the mass of the object? (c) If the object is initially at rest, what is its speed after 10. 0 s? (d) What are the velocity components of the object after 10. 0 s? where represents the direction of a at
Three forces, given by , , and , act on an object to give it an acceleration of magnitude 3. 75 m/s 2. (a) What is the direction of the acceleration? (b) What is the mass of the object? (c) If the object is initially at rest, what is its speed after 10. 0 s? (d) What are the velocity components of the object after 10. 0 s? where represents the direction of a at
 Three forces, given by , , and , act on an object to give it an acceleration of magnitude 3. 75 m/s 2. (a) What is the direction of the acceleration? (b) What is the mass of the object? (c) If the object is initially at rest, what is its speed after 10. 0 s? (d) What are the velocity components of the object after 10. 0 s? (a) (b) (d) (c) counterclockwise from the x-axis
Three forces, given by , , and , act on an object to give it an acceleration of magnitude 3. 75 m/s 2. (a) What is the direction of the acceleration? (b) What is the mass of the object? (c) If the object is initially at rest, what is its speed after 10. 0 s? (d) What are the velocity components of the object after 10. 0 s? (a) (b) (d) (c) counterclockwise from the x-axis
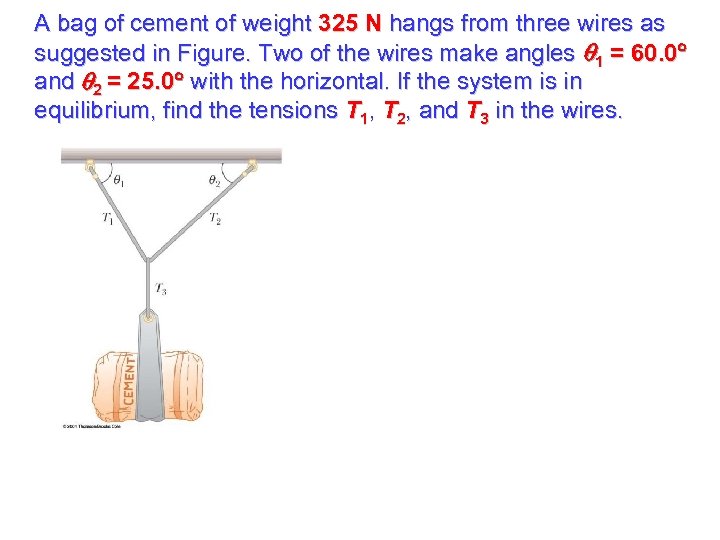 A bag of cement of weight 325 N hangs from three wires as suggested in Figure. Two of the wires make angles 1 = 60. 0 and 2 = 25. 0 with the horizontal. If the system is in equilibrium, find the tensions T 1, T 2, and T 3 in the wires.
A bag of cement of weight 325 N hangs from three wires as suggested in Figure. Two of the wires make angles 1 = 60. 0 and 2 = 25. 0 with the horizontal. If the system is in equilibrium, find the tensions T 1, T 2, and T 3 in the wires.
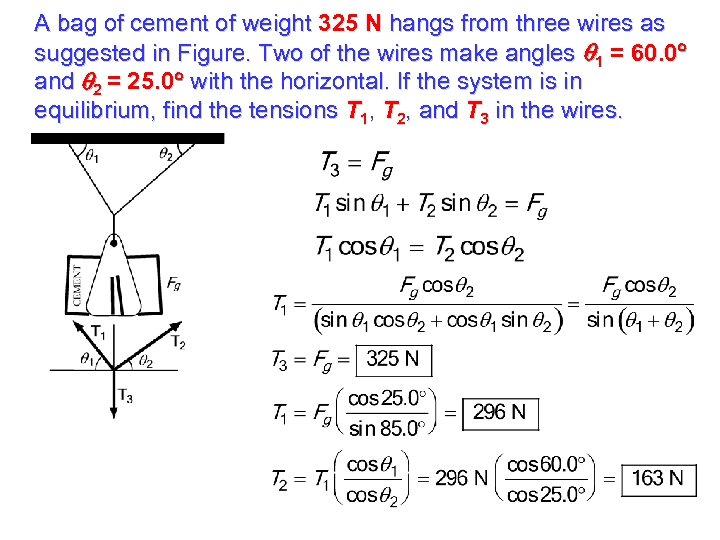 A bag of cement of weight 325 N hangs from three wires as suggested in Figure. Two of the wires make angles 1 = 60. 0 and 2 = 25. 0 with the horizontal. If the system is in equilibrium, find the tensions T 1, T 2, and T 3 in the wires.
A bag of cement of weight 325 N hangs from three wires as suggested in Figure. Two of the wires make angles 1 = 60. 0 and 2 = 25. 0 with the horizontal. If the system is in equilibrium, find the tensions T 1, T 2, and T 3 in the wires.
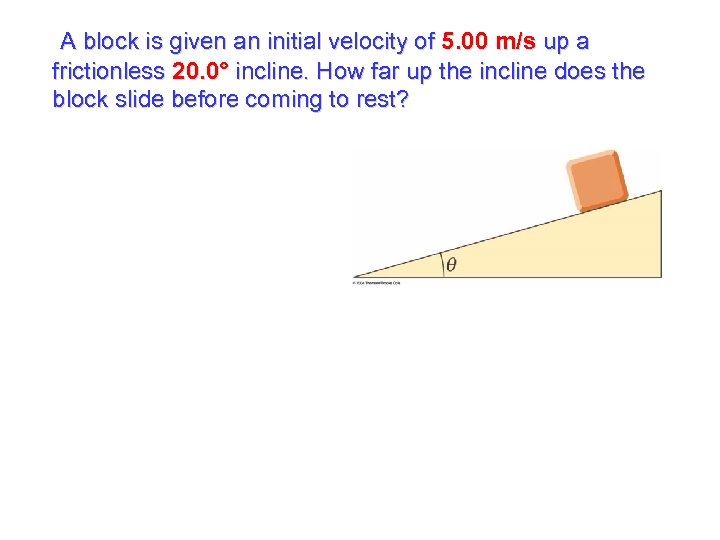 A block is given an initial velocity of 5. 00 m/s up a frictionless 20. 0° incline. How far up the incline does the block slide before coming to rest?
A block is given an initial velocity of 5. 00 m/s up a frictionless 20. 0° incline. How far up the incline does the block slide before coming to rest?
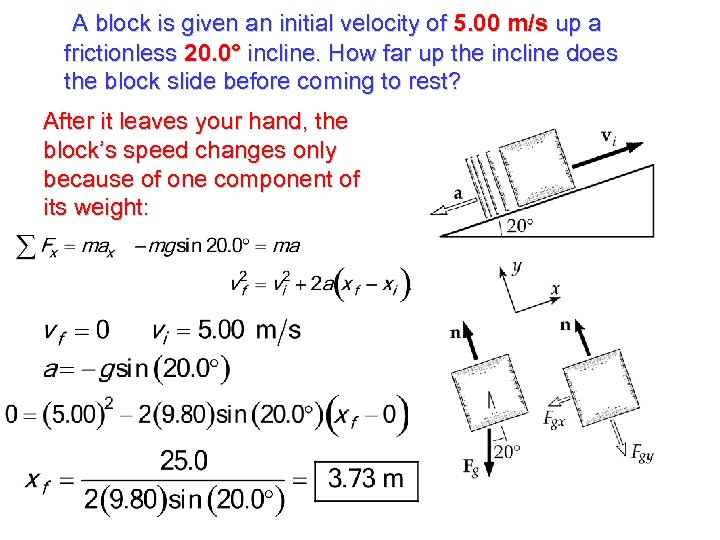 A block is given an initial velocity of 5. 00 m/s up a frictionless 20. 0° incline. How far up the incline does the block slide before coming to rest? After it leaves your hand, the block’s speed changes only because of one component of its weight:
A block is given an initial velocity of 5. 00 m/s up a frictionless 20. 0° incline. How far up the incline does the block slide before coming to rest? After it leaves your hand, the block’s speed changes only because of one component of its weight:
 A woman at an airport is towing her 20. 0 -kg suitcase at constant speed by pulling on a strap at an angle above the horizontal. She pulls on the strap with a 35. 0 -N force, and the friction force on the suitcase is 20. 0 N. Draw a free -body diagram of the suitcase. (a) What angle does the strap make with the horizontal? (b) What normal force does the ground exert on the suitcase?
A woman at an airport is towing her 20. 0 -kg suitcase at constant speed by pulling on a strap at an angle above the horizontal. She pulls on the strap with a 35. 0 -N force, and the friction force on the suitcase is 20. 0 N. Draw a free -body diagram of the suitcase. (a) What angle does the strap make with the horizontal? (b) What normal force does the ground exert on the suitcase?
 A woman at an airport is towing her 20. 0 -kg suitcase at constant speed by pulling on a strap at an angle above the horizontal. She pulls on the strap with a 35. 0 -N force, and the friction force on the suitcase is 20. 0 N. Draw a free -body diagram of the suitcase. (a) What angle does the strap make with the horizontal? (b) What normal force does the ground exert on the suitcase? (a)
A woman at an airport is towing her 20. 0 -kg suitcase at constant speed by pulling on a strap at an angle above the horizontal. She pulls on the strap with a 35. 0 -N force, and the friction force on the suitcase is 20. 0 N. Draw a free -body diagram of the suitcase. (a) What angle does the strap make with the horizontal? (b) What normal force does the ground exert on the suitcase? (a)
 A woman at an airport is towing her 20. 0 -kg suitcase at constant speed by pulling on a strap at an angle above the horizontal. She pulls on the strap with a 35. 0 -N force, and the friction force on the suitcase is 20. 0 N. Draw a free -body diagram of the suitcase. (a) What angle does the strap make with the horizontal? (b) What normal force does the ground exert on the suitcase? (b)
A woman at an airport is towing her 20. 0 -kg suitcase at constant speed by pulling on a strap at an angle above the horizontal. She pulls on the strap with a 35. 0 -N force, and the friction force on the suitcase is 20. 0 N. Draw a free -body diagram of the suitcase. (a) What angle does the strap make with the horizontal? (b) What normal force does the ground exert on the suitcase? (b)
 Three objects are connected on the table as shown in Figure. The table is rough and has a coefficient of kinetic friction of 0. 350. The objects have masses 4. 00 kg, 1. 00 kg and 2. 00 kg, as shown, and the pulleys are frictionless. Draw free-body diagrams of each of the objects. (a) Determine the acceleration of each object and their directions. (b) Determine the tensions in the two cords.
Three objects are connected on the table as shown in Figure. The table is rough and has a coefficient of kinetic friction of 0. 350. The objects have masses 4. 00 kg, 1. 00 kg and 2. 00 kg, as shown, and the pulleys are frictionless. Draw free-body diagrams of each of the objects. (a) Determine the acceleration of each object and their directions. (b) Determine the tensions in the two cords.
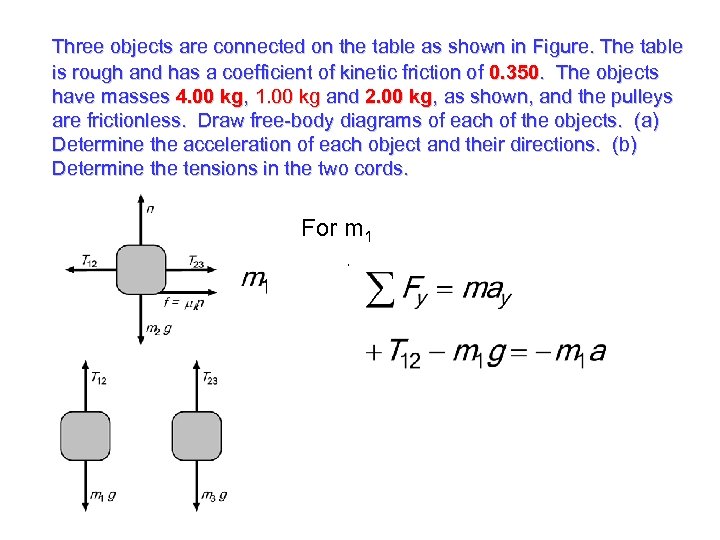 Three objects are connected on the table as shown in Figure. The table is rough and has a coefficient of kinetic friction of 0. 350. The objects have masses 4. 00 kg, 1. 00 kg and 2. 00 kg, as shown, and the pulleys are frictionless. Draw free-body diagrams of each of the objects. (a) Determine the acceleration of each object and their directions. (b) Determine the tensions in the two cords. For m 1 ,
Three objects are connected on the table as shown in Figure. The table is rough and has a coefficient of kinetic friction of 0. 350. The objects have masses 4. 00 kg, 1. 00 kg and 2. 00 kg, as shown, and the pulleys are frictionless. Draw free-body diagrams of each of the objects. (a) Determine the acceleration of each object and their directions. (b) Determine the tensions in the two cords. For m 1 ,


