Chapter 5 Demand Food A B Budget line

Chapter 5: Demand Food A B Budget line Clothes Question: Given that a person can consume a combination of food and clothes at any point on the budget line, which point would satisfy the person the most? A or B or any other point? 1

Demand • People allocate their limited income among different goods and services to maximize their satisfaction. – Utility: the satisfaction people derive from consumption • Subjective • Not comparable between people • Individuals’ goal is to maximize their utility – Revisit the cost-benefit principle • People would consume one more unit of food only if the marginal utility of doing so is at least as large as its cost, which is the utility lost from the reduction in the consumption of clothes. 2

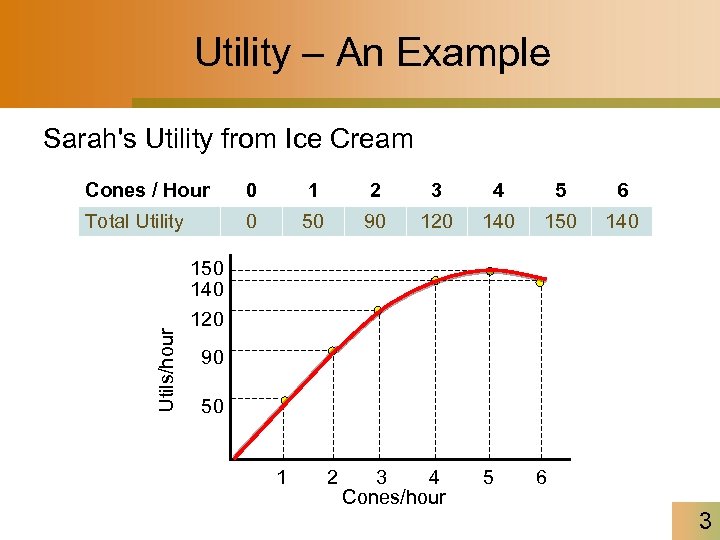
Utility – An Example Sarah's Utility from Ice Cream 0 1 2 3 4 5 6 Total Utility 0 50 90 120 140 150 140 Utils/hour Cones / Hour 150 140 120 90 50 1 2 3 4 Cones/hour 5 6 3

Utility – An Example (Cont. ) Sarah's Marginal Utility from Ice Cream Cones / Hour 0 1 2 3 4 5 6 Total Utility 0 50 90 120 140 150 140 Marginal Utility 50 40 30 20 10 -10 §Marginal utility: the additional utility from consuming one more Change in utility Marginal utility = Change in consumption 4

Diminishing Marginal Utility As consumption increases beyond some point , the marginal utility gained from consuming additional unit of a good tends to decrease. 5

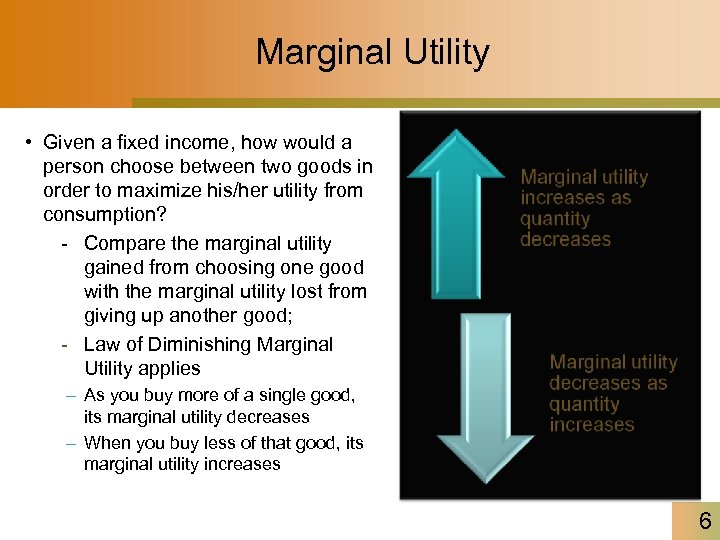
Marginal Utility • Given a fixed income, how would a person choose between two goods in order to maximize his/her utility from consumption? - Compare the marginal utility gained from choosing one good with the marginal utility lost from giving up another good; - Law of Diminishing Marginal Utility applies 1 – As you buy P more of a single good, x ε =marginal utility decreases its Q slope – When you buy less of that good, its marginal utility increases 6

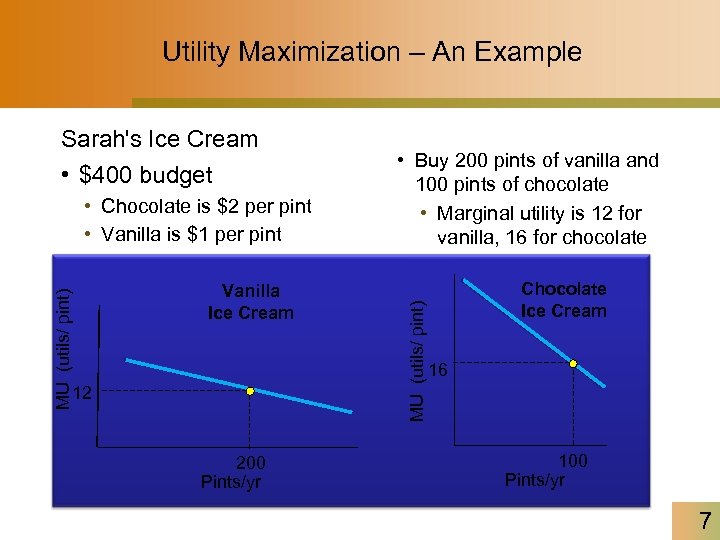
Utility Maximization – An Example • $400 budget ε = MU (utils/ pint) • Chocolate is $2 per pint • Vanilla is $1 per pint Vanilla Ice Cream 12 200 Pints/yr P Q • Buy 1 200 pints of vanilla and x 100 pints of chocolate slope • Marginal utility is 12 for vanilla, 16 for chocolate MU (utils/ pint) Sarah's Ice Cream Chocolate Ice Cream 16 100 Pints/yr 7

Utility Maximization – An Example • Susan can increase her utility by consuming less Chocolate and more Vanilla – Reduce one pint of chocolate saves her $2, with which Susan can buy two more pints of vanilla ($1 per pint); – Marginal utility lost from giving up one pint of chocolate = 16 utils; – Marginal utility gained from two more pints of vanilla = 2 x 12=24 utils; – Gain > Loss, Susan should buy more vanilla and less chocolate; – So, under what conditions would Susan maximizes her total utility? In other words, what is the optimal combination of chocolate and vanilla that gratifies Susan the most? 8

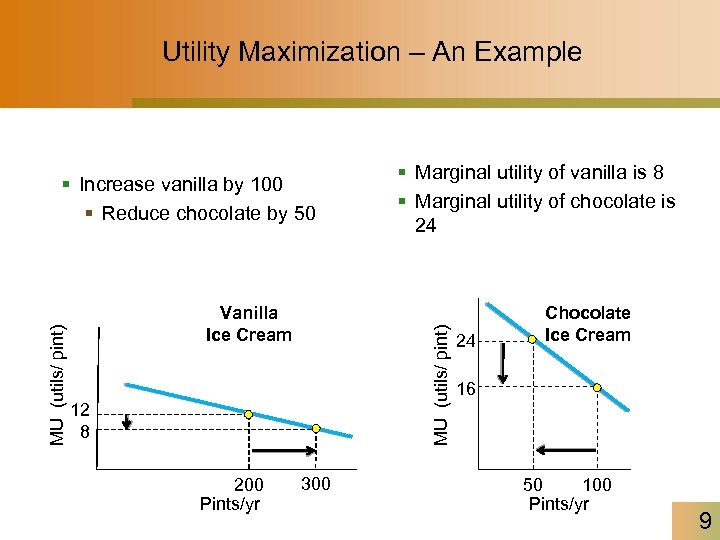
Utility Maximization – An Example Vanilla Ice Cream 12 8 200 Pints/yr § Marginal utility of vanilla is 8 § Marginal utility of chocolate is 24 MU (utils/ pint) § Increase vanilla by 100 § Reduce chocolate by 50 300 24 Chocolate Ice Cream 16 50 100 Pints/yr 9

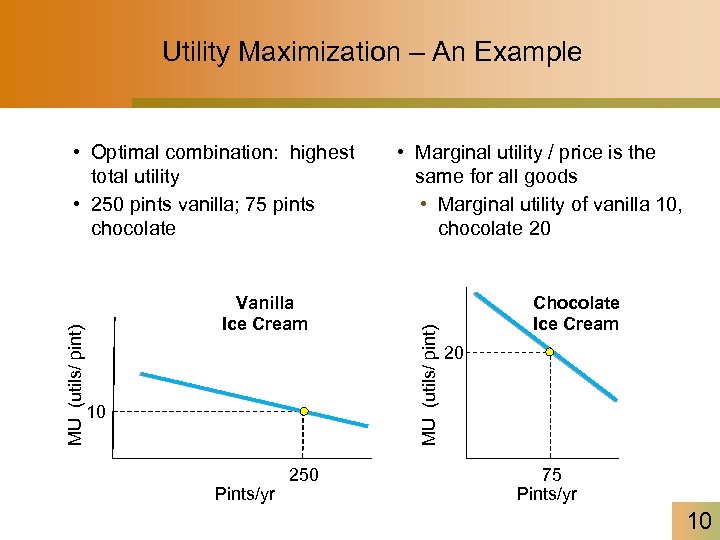
Utility Maximization – An Example Vanilla Ice Cream 10 Pints/yr 250 • Marginal utility / price is the same for all goods • Marginal utility of vanilla 10, chocolate 20 MU (utils/ pint) • Optimal combination: highest total utility • 250 pints vanilla; 75 pints chocolate Chocolate Ice Cream 20 75 Pints/yr 10

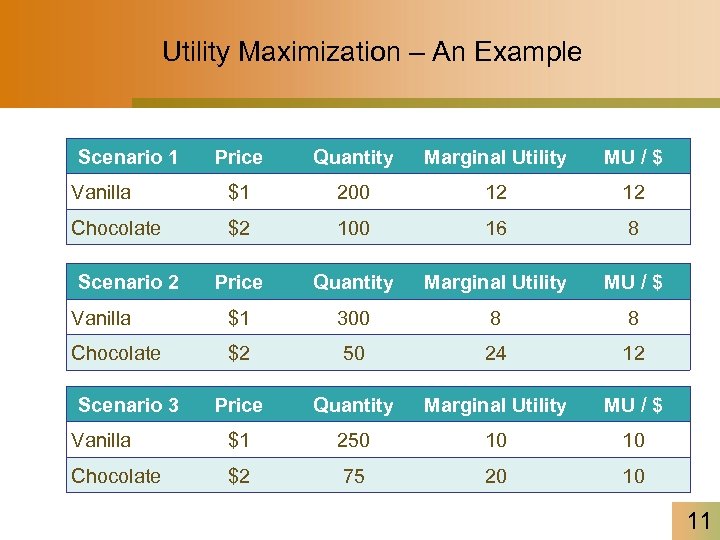
Utility Maximization – An Example Scenario 1 Price Quantity Marginal Utility MU / $ Vanilla $1 200 12 12 Chocolate $2 100 16 8 Price Quantity Marginal Utility MU / $ Vanilla $1 300 8 8 Chocolate $2 50 24 12 Price Quantity Marginal Utility MU / $ Vanilla $1 250 10 10 Chocolate $2 75 20 10 Scenario 2 Scenario 3 11

Rational Spending Rule The Rational Spending Rule Spending should be allocated across goods so that the marginal utility per dollar is the same for each good MU 1 / P 1 = MU 2 / P 2 12

Rational Spending Rule • Substitution effect – Suppose, one starts with MU 1/P 1=MU 2/ P 2; – When P 1 increases, MU 1/P 1<MU 2/ P 2; – According to the rational spending rule, one should increase spending on good 2 and reduce spending on good 1 until MU 1/P 1=MU 2/ P 2 again; – So explained is the substitution effect. 13

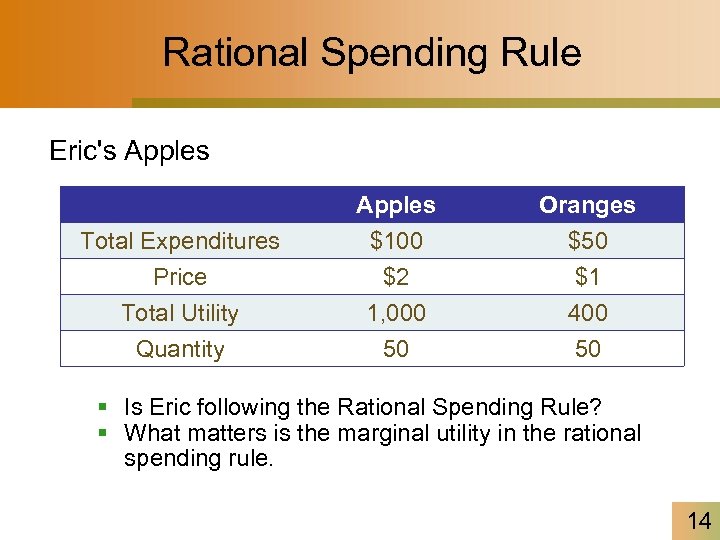
Rational Spending Rule Eric's Apples Total Expenditures Price Total Utility Apples $100 $2 1, 000 Oranges $50 $1 400 Quantity 50 50 § Is Eric following the Rational Spending Rule? § What matters is the marginal utility in the rational spending rule. 14

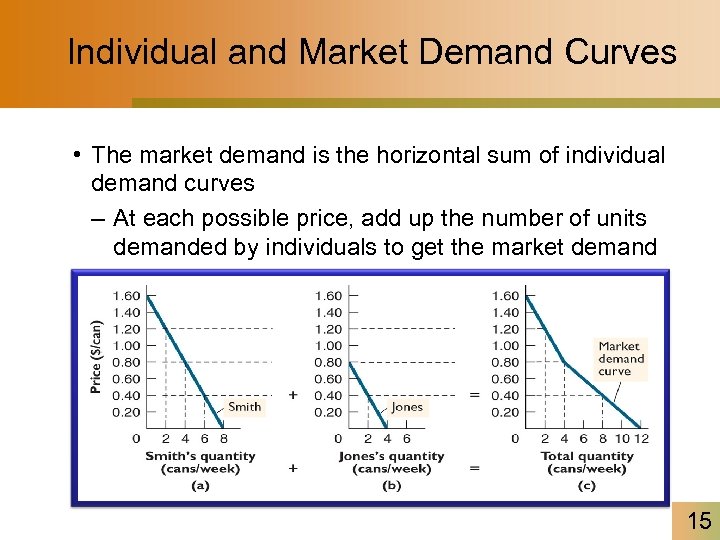
Individual and Market Demand Curves • The market demand is the horizontal sum of individual demand curves – At each possible price, add up the number of units demanded by individuals to get the market demand 15

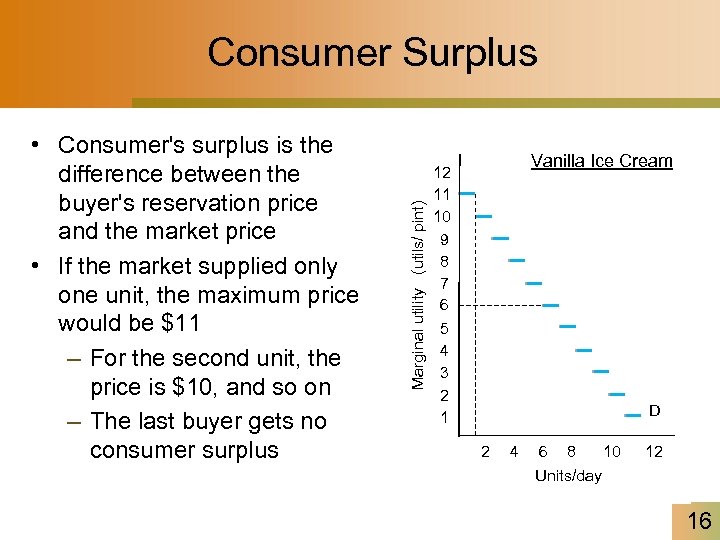
• Consumer's surplus is the difference between the buyer's reservation price and the market price • If the market supplied only one unit, the maximum price would be $11 – For the second unit, the price is $10, and so on – The last buyer gets no consumer surplus Marginal utility (utils/ pint) Consumer Surplus Vanilla Ice Cream 12 11 10 9 8 7 6 5 4 3 2 1 D 2 4 6 8 10 Units/day 12 16

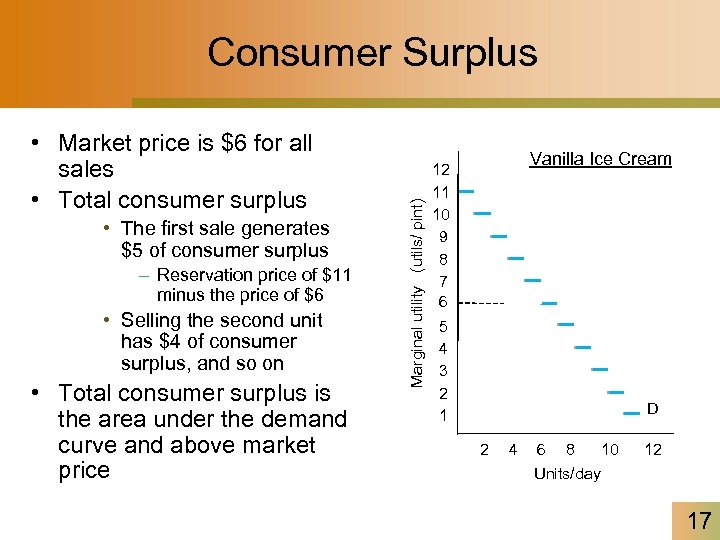
• Market price is $6 for all sales • Total consumer surplus • The first sale generates $5 of consumer surplus – Reservation price of $11 minus the price of $6 • Selling the second unit has $4 of consumer surplus, and so on • Total consumer surplus is the area under the demand curve and above market price Marginal utility (utils/ pint) Consumer Surplus Vanilla Ice Cream 12 11 10 9 8 7 6 5 4 3 2 1 D 2 4 6 8 10 Units/day 12 17

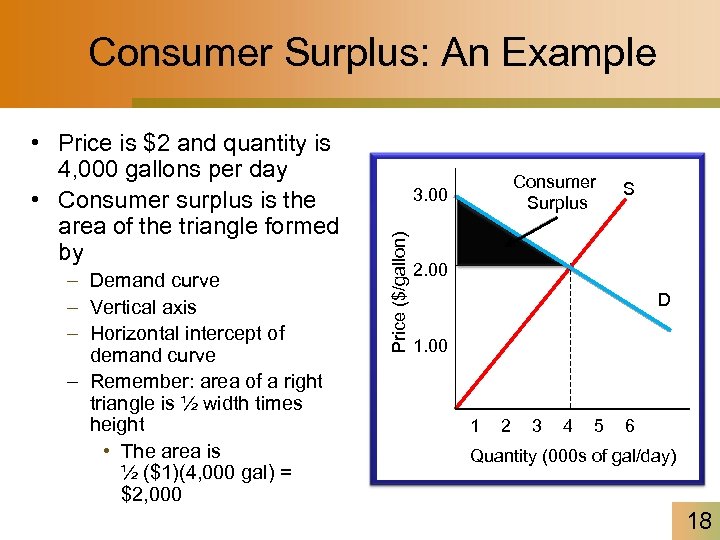
Consumer Surplus: An Example – Demand curve – Vertical axis – Horizontal intercept of demand curve – Remember: area of a right triangle is ½ width times height • The area is ½ ($1)(4, 000 gal) = $2, 000 Consumer Surplus 3. 00 Price ($/gallon) • Price is $2 and quantity is 4, 000 gallons per day • Consumer surplus is the area of the triangle formed by S 2. 00 D 1. 00 1 2 3 4 5 6 Quantity (000 s of gal/day) 18