6d0fce661fc7a9c76be6979dab647c5e.ppt
- Количество слайдов: 92

Chapter 4: The Building Blocks: Binary Numbers, Boolean Logic, and Gates Invitation to Computer Science, C++ Version, Third Edition

Objectives In this chapter, you will learn about: n Boolean logic and gates n The binary numbering system n Building computer circuits n Control circuits Invitation to Computer Science, C++ Version, Third Edition 2

Introduction n Chapter 4 focuses on hardware design (also called logic design) q q q How to represent and store information inside a computer How to use the principles of symbolic logic to design gates How to use gates to construct circuits that perform operations such as adding and comparing numbers, and fetching instructions Invitation to Computer Science, C++ Version, Third Edition 3

The Reliability of Binary Representation Sec 4. 2. 3 n Electronic devices are most reliable in a bistable environment n Bistable environment q Distinguishes only two electronic states n n n Current flowing or not Direction of flow Easiest way to make computers reliable was to use a two-state design. Hence they are designed to store and process binary information. Invitation to Computer Science, C++ Version, Third Edition 4

Binary Storage Devices n Sec 4. 2. 4 Magnetic core q q q Historic device for computer memory Tiny magnetized rings: flow of current sets the direction of magnetic field Binary values 0 and 1 are represented using the direction of the magnetic field Invitation to Computer Science, C++ Version, Third Edition 5
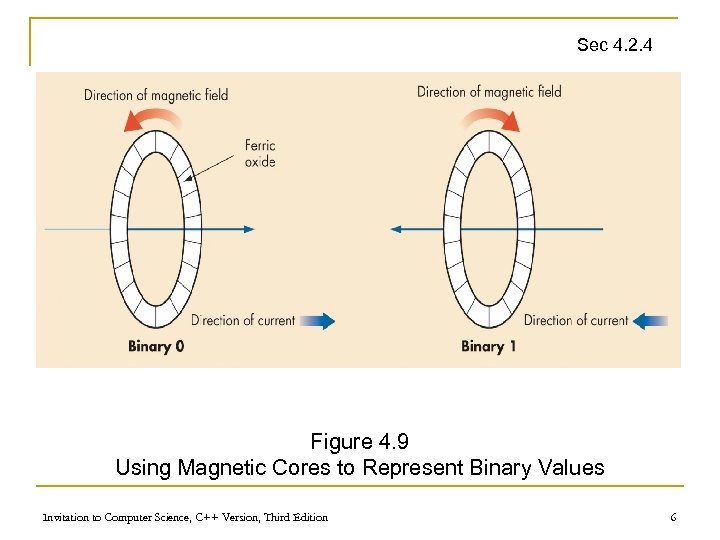
Sec 4. 2. 4 Figure 4. 9 Using Magnetic Cores to Represent Binary Values Invitation to Computer Science, C++ Version, Third Edition 6

Binary Storage Devices (continued) Sec 4. 2. 4 n Transistors q Solid-state switches: either permits or blocks current flow q A control input causes state change q Constructed from semiconductors Invitation to Computer Science, C++ Version, Third Edition 7
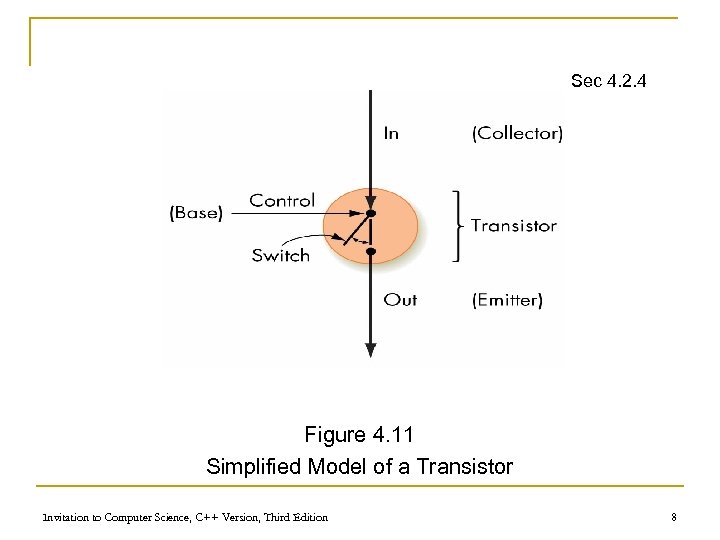
Sec 4. 2. 4 Figure 4. 11 Simplified Model of a Transistor Invitation to Computer Science, C++ Version, Third Edition 8
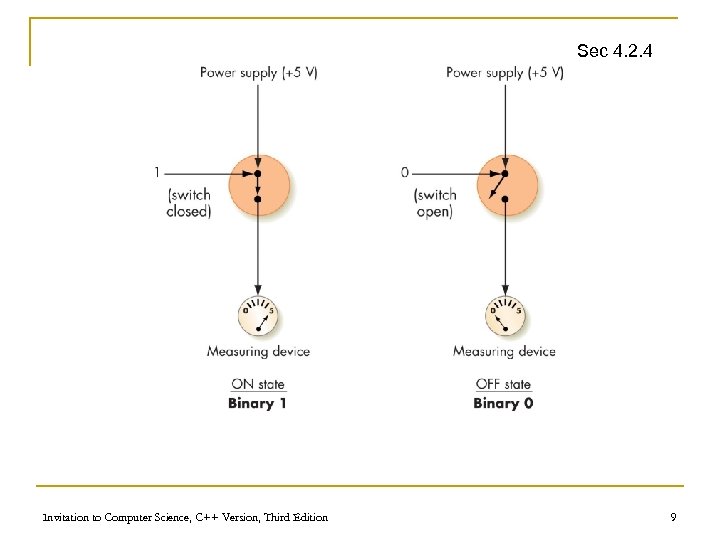
Sec 4. 2. 4 Invitation to Computer Science, C++ Version, Third Edition 9
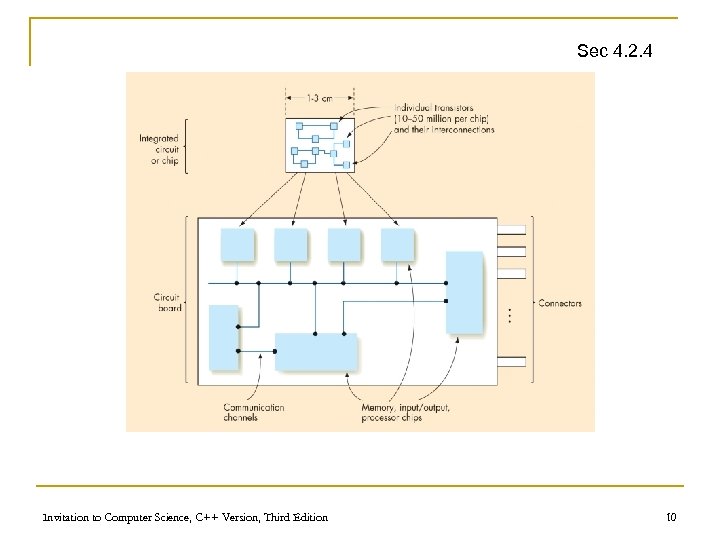
Sec 4. 2. 4 Invitation to Computer Science, C++ Version, Third Edition 10

Boolean Logic and Gates: Boolean Logic Sec 4. 3. 1 n Boolean logic is a branch of mathematics which describes operations on objects with two possible values, True or False n True/False values map easily onto a two-state electronic environment. n Boolean logic operations may be performed on electronic signals using devices built out of transistors and other electronic devices. Invitation to Computer Science, C++ Version, Third Edition 11

Boolean Logic (continued) Sec 4. 3. 1 n Let a and b represent objects with two possible values, true and false n Boolean logic operations q a AND b n q a OR b n q True only when a is true and b is true True when either a is true or b is true, or both are true NOT a n True when a is false, and vice versa Invitation to Computer Science, C++ Version, Third Edition 12

Boolean Logic (continued) n Boolean expressions q Constructed by combining together Boolean operations n n Sec 4. 3. 1 Example: (a AND b) OR ((NOT b) AND (NOT a)) Truth tables capture the output/value of a Boolean expression q A column for each input plus the output q A row for each combination of input values Invitation to Computer Science, C++ Version, Third Edition 13
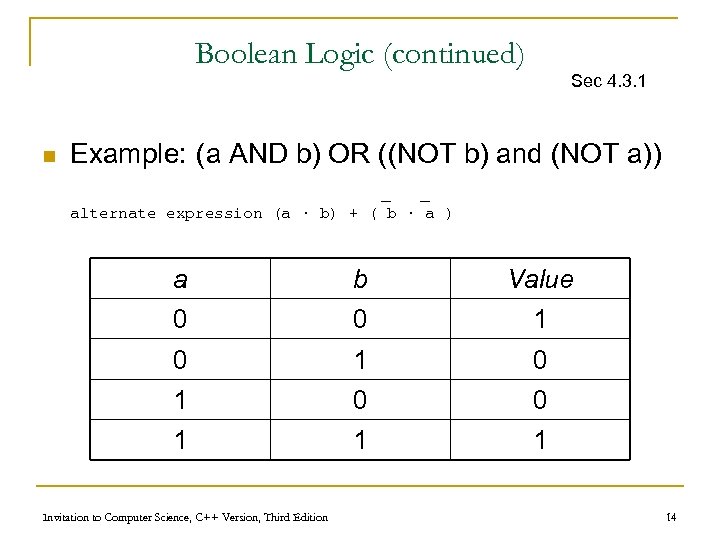
Boolean Logic (continued) n Sec 4. 3. 1 Example: (a AND b) OR ((NOT b) and (NOT a)) _ _ alternate expression (a ∙ b) + ( b ∙ a ) a b Value 0 0 1 0 1 0 0 1 1 1 Invitation to Computer Science, C++ Version, Third Edition 14

Gates n Gates q n Sec 4. 3. 2 Hardware devices built from transistors to mimic Boolean logical operations on digital electrical signals AND gate q Two input lines, one output line q Outputs a 1 when both inputs are 1 Invitation to Computer Science, C++ Version, Third Edition 15

Gates (continued) Sec 4. 3. 2 n OR gate q q n Two input lines, one output line Outputs a 1 when either input is 1 NOT gate q One input line, one output line q Outputs a 1 when input is 0 and vice versa Invitation to Computer Science, C++ Version, Third Edition 16
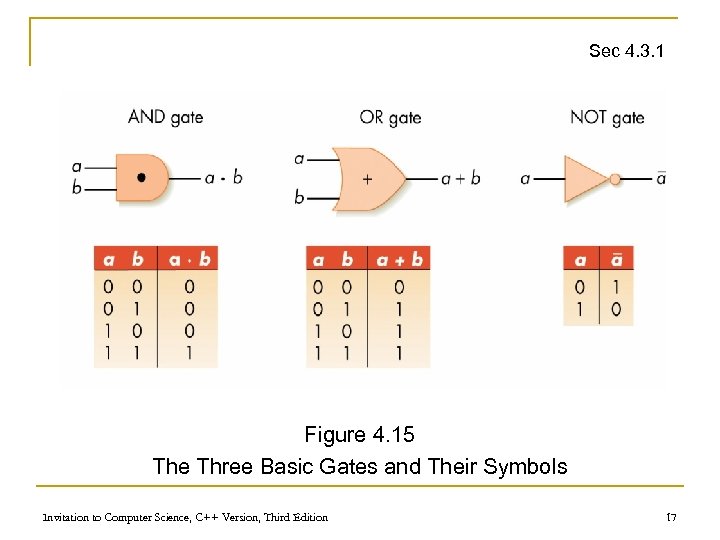
Sec 4. 3. 1 Figure 4. 15 The Three Basic Gates and Their Symbols Invitation to Computer Science, C++ Version, Third Edition 17
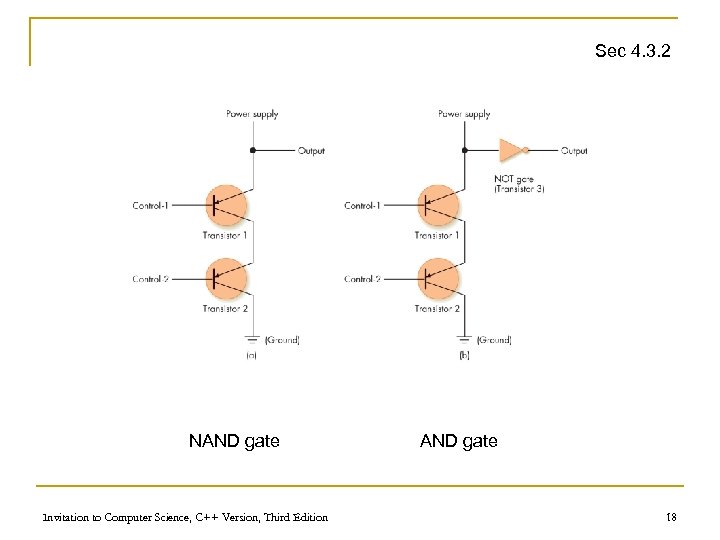
Sec 4. 3. 2 NAND gate Invitation to Computer Science, C++ Version, Third Edition AND gate 18
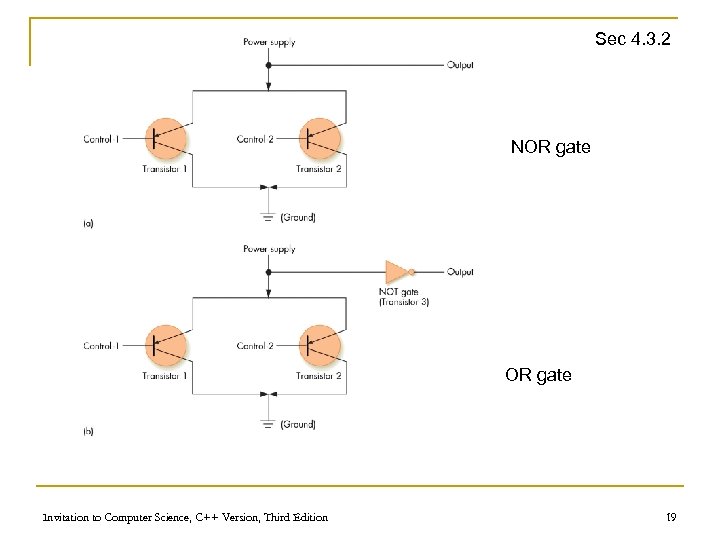
Sec 4. 3. 2 NOR gate Invitation to Computer Science, C++ Version, Third Edition 19
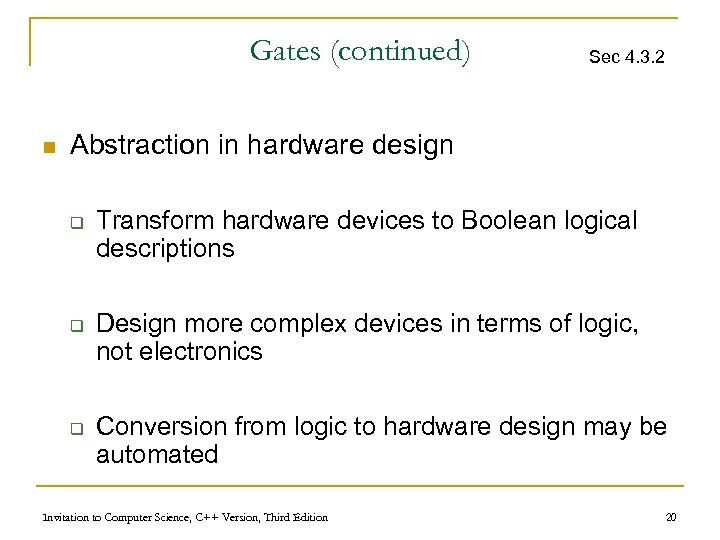
Gates (continued) n Sec 4. 3. 2 Abstraction in hardware design q q q Transform hardware devices to Boolean logical descriptions Design more complex devices in terms of logic, not electronics Conversion from logic to hardware design may be automated Invitation to Computer Science, C++ Version, Third Edition 20
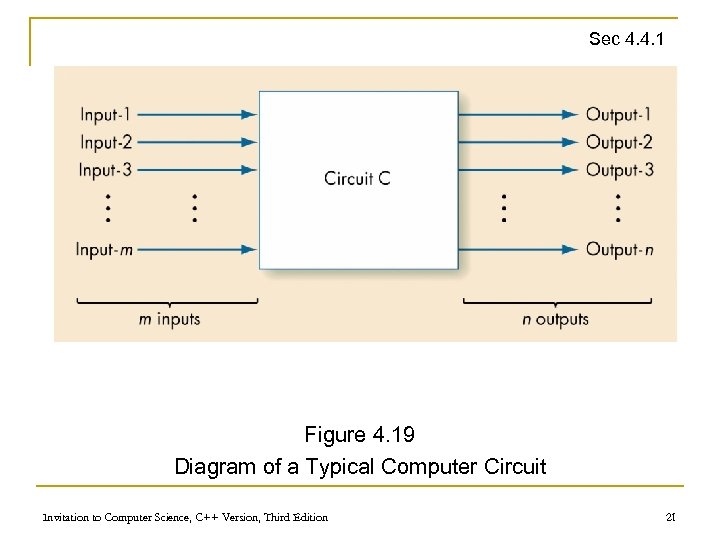
Sec 4. 4. 1 Figure 4. 19 Diagram of a Typical Computer Circuit Invitation to Computer Science, C++ Version, Third Edition 21

Building Computer Circuits: Introduction Sec 4. 4. 1 n A circuit is a collection of logic gates: q q n Transforms a set of binary inputs into a set of binary outputs Values of the outputs depend only on the current values of the inputs Combinational circuits have no cycles in them (no outputs feed back into their own inputs) Invitation to Computer Science, C++ Version, Third Edition 22
Invitation to Computer Science, C++ Version, Third Edition 23
Invitation to Computer Science, C++ Version, Third Edition 24

Building Computer Circuits: Intro Cont’d. Sec 4. 4. 1 inputs a 0 0 1 1 b 0 1 output c 1 0 0 0 We want a 1 only when both inputs are 0. Is there a gate which will do this? An AND gate gives a 1 only when both inputs are 1. An OR gate gives a 1 whenever at least one input is 1 Could we use an AND gate or an OR gate somehow? Invitation to Computer Science, C++ Version, Third Edition 25

A Circuit Construction Algorithm n Sec 4. 4. 2 Sum-of-products algorithm is one way to design circuits: q Truth table to Boolean expression to gate layout Invitation to Computer Science, C++ Version, Third Edition 26

Sec 4. 4. 2 Figure 4. 21 The Sum-of-Products Circuit Construction Algorithm Invitation to Computer Science, C++ Version, Third Edition 27

A Circuit Construction Algorithm (continued) Sec 4. 4. 2 n Sum-of-products algorithm q q Truth table captures every input/output possible for circuit Repeat process for each output line n Build a Boolean expression using AND and NOT for each 1 of the output line n Combine together all the expressions with ORs n Build circuit from whole Boolean expression Invitation to Computer Science, C++ Version, Third Edition 28

The Binary Numbering System n A computer’s internal storage techniques are different from the way people represent information in daily lives n Information inside a digital computer is stored as a collection of binary data Invitation to Computer Science, C++ Version, Third Edition 29

Binary Representation of Numeric and Textual Information n Binary numbering system q q q Base-2 Built from ones and zeros Each position is a power of 2 1101 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 n Decimal numbering system q q Base-10 Each position is a power of 10 3052 = 3 x 103 + 0 x 102 + 5 x 101 + 2 x 100 Invitation to Computer Science, C++ Version, Third Edition 30
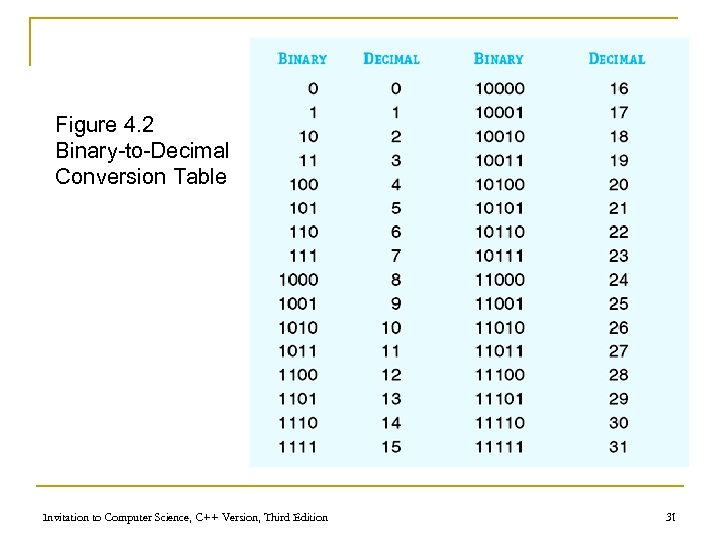
Figure 4. 2 Binary-to-Decimal Conversion Table Invitation to Computer Science, C++ Version, Third Edition 31

Taxonomy of Integers Invitation to Computer Science, C++ Version, Third Edition 32

Binary Representation of Numeric and Textual Information (continued) n Representing integers q q Decimal integers are converted to binary integers Given k bits, the largest unsigned integer is 2 k - 1 n q Given 4 bits, the largest is 24 -1 = 15 Signed integers must also represent the sign (positive or negative) Invitation to Computer Science, C++ Version, Third Edition 33

Binary to Decimal Conversion Invitation to Computer Science, C++ Version, Third Edition 34
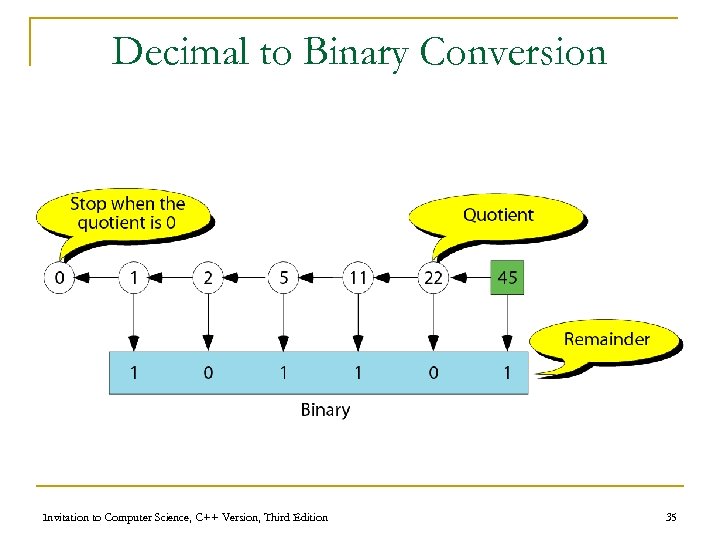
Decimal to Binary Conversion Invitation to Computer Science, C++ Version, Third Edition 35

Two’s Complement Representation of Signed Integers n n Used by almost all computers today All places hold the value they would in binary except for the leftmost place which is negative q q n If last bit (leftmost) q q n 8 bit integer: -128 64 32 16 8 4 2 1 Range: [-128, 127] is 0, then positive looks just as before is 1, then negative add values for first 7 digits and then subtract 128 1000 1101 = 1+4+8 -128 = -115 Invitation to Computer Science, C++ Version, Third Edition 36

Two’s Complement Representation of Signed Integers n Converting from decimal to 2’s complement q For positive numbers: find the binary representation q For negative numbers: n n Find the binary representation for its positive equivalent Flip all bits Add a 1 43 43 = 0010 1011 -43 q 43 = 0010 1011 1101 0100 1101 0101 q 1101 0101 = -128+64+16+4+1 = -43 We can use the usual laws of binary addition q n n Invitation to Computer Science, C++ Version, Third Edition 37

Two’s Complement Representation n 125 - 19 = 106 0111 1101 1110 1101 ------0110 1010 = 106 ! What happened to the one that we carried at the end? q Got lost but still we got the right answer! n We carried into and carried out of the leftmost column Invitation to Computer Science, C++ Version, Third Edition 38

Binary Representation of Numeric and Textual Information (continued) n Representing real numbers q Real numbers may be put into binary scientific notation: a x 2 b n q Number then normalized so that first significant digit is immediately to the right of the binary point n q Example: 101. 11 x 20 Example: . 10111 x 23 Mantissa and exponent then stored Invitation to Computer Science, C++ Version, Third Edition 39
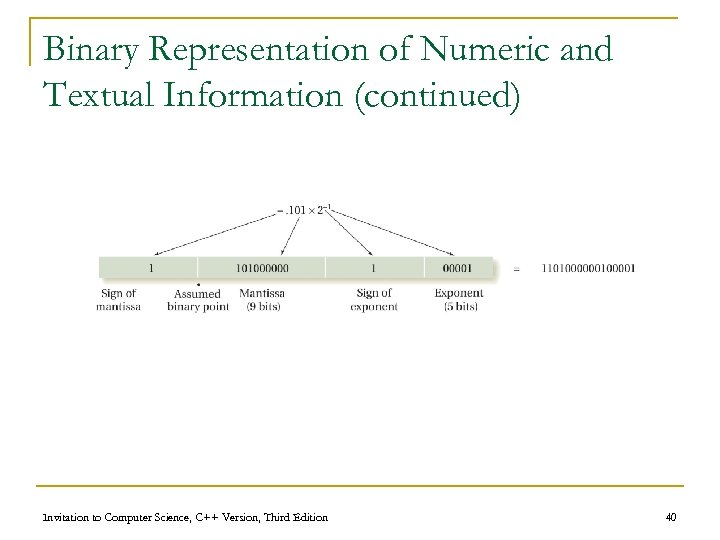
Binary Representation of Numeric and Textual Information (continued) Invitation to Computer Science, C++ Version, Third Edition 40
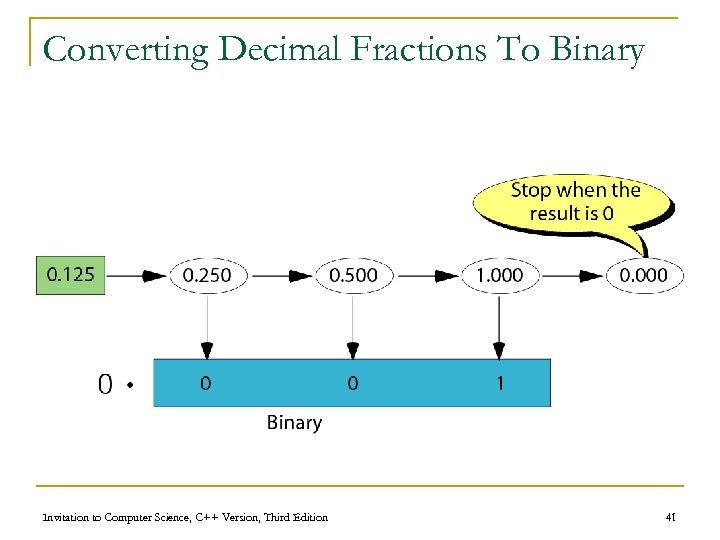
Converting Decimal Fractions To Binary Invitation to Computer Science, C++ Version, Third Edition 41

Converting Decimal Fractions To Binary • Note that the binary representation of 0. 410 is a repeating base two fraction, . 01102 This just says that 0. 4 cannot be exactly represented as a sum of inverse powers of two. . 875 = • . 400 = • • Invitation to Computer Science, C++ Version, Third Edition 42

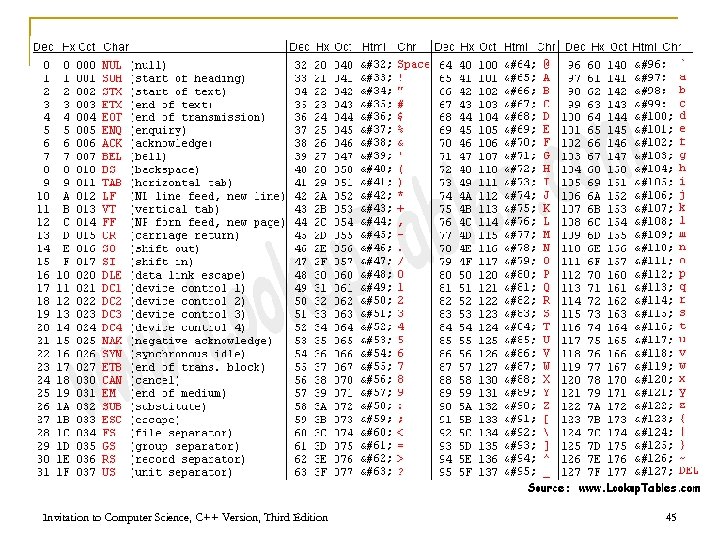
Binary Representation of Textual Information § § Many transformations exist and all are arbitrary Two popular § § EBCDIC (Extended Binary Coded Decimal Interchange Code) by IBM ASCII (American Standard Code for Information Interchange) by American National Standards Institute (ANSI) § § § Most widely used § Every letter/symbol is represented by 7 bits § How many letters/symbols do we have in total? A-Z (26) , a-z (26) , 0 -9 (10), symbols (33), control characters (33) If using 1 byte/character we have one extra bit § Extended ASCII-8 (more mathematical and graphical symbols or phonetic marks) --- 256 Invitation to Computer Science, C++ Version, Third Edition 43

Binary Representation of Numeric and Textual Information (continued) n Characters are mapped onto binary numbers q ASCII code set n q UNICODE code set n n 8 bits per character; 256 character codes 16 bits per character; 65, 536 character codes Text strings are sequences of characters in some encoding Invitation to Computer Science, C++ Version, Third Edition 44
Invitation to Computer Science, C++ Version, Third Edition 45

Binary Representation of Images n Representing image data q q q Images are sampled by reading color and intensity values at even intervals across the image Each sampled point is a pixel Image quality depends on number of bits at each pixel Invitation to Computer Science, C++ Version, Third Edition 46

Binary Representation of Images Divide the screen into a grid of cells each referred to as a pixel 512*256 image grid has 512 columns and 256 rows Pixel values and sizes depend on the type of the image For black & white images, we can use 1 bit for every pixel such that 1 black and 0 white For grayscale images, we use 1 byte where 255 black and 0 white and anything in between is gray (higher/lower values are closer to black/white) For color images, we need three values per pixel (depends on the color scheme used): Red/Green/Blue We need 1 byte per value 3 bytes per pixel For an 512 x 256 image 512 x 256 x 3 = 384 K bytes Invitation to Computer Science, C++ Version, Third Edition 47
Invitation to Computer Science, C++ Version, Third Edition 48

Invitation to Computer Science, C++ Version, Third Edition 49

Invitation to Computer Science, C++ Version, Third Edition 50

Binary Representation of Movies q Image movies are built from a number of images (or frames) that are displayed in a certain sequence at high speeds n n 30 frames per second 2 -hr movie needs (assume previous image used) q n 384 K * 30 * 60 * 120 = 83 GB (billion) bytes! People use compression to reduce large movie sizes Usually the change between two consecutive images is small store only difference between frames (Temporal compression) q Large areas with the same color can be stored by saving the boundary pixels only (everything within the boundaries has the same value) (Spatial compression) q Invitation to Computer Science, C++ Version, Third Edition 51
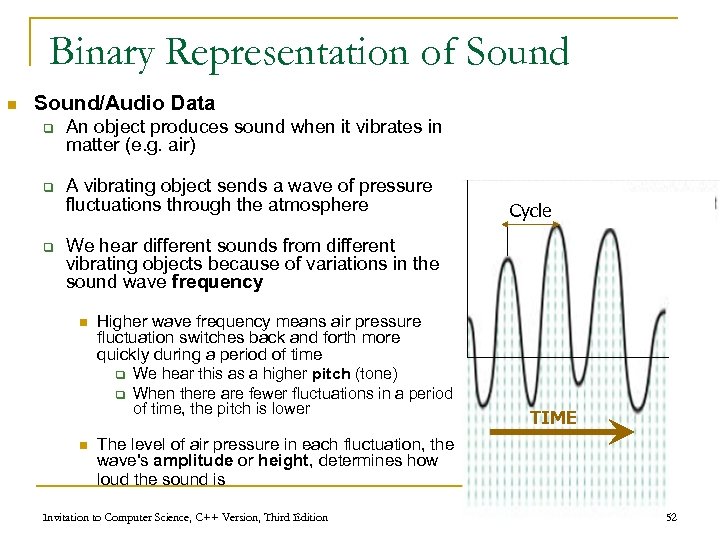
Binary Representation of Sound n Sound/Audio Data q q q An object produces sound when it vibrates in matter (e. g. air) A vibrating object sends a wave of pressure fluctuations through the atmosphere Cycle We hear different sounds from different vibrating objects because of variations in the sound wave frequency n Higher wave frequency means air pressure fluctuation switches back and forth more quickly during a period of time q q n We hear this as a higher pitch (tone) When there are fewer fluctuations in a period of time, the pitch is lower TIME The level of air pressure in each fluctuation, the wave's amplitude or height, determines how loud the sound is Invitation to Computer Science, C++ Version, Third Edition 52

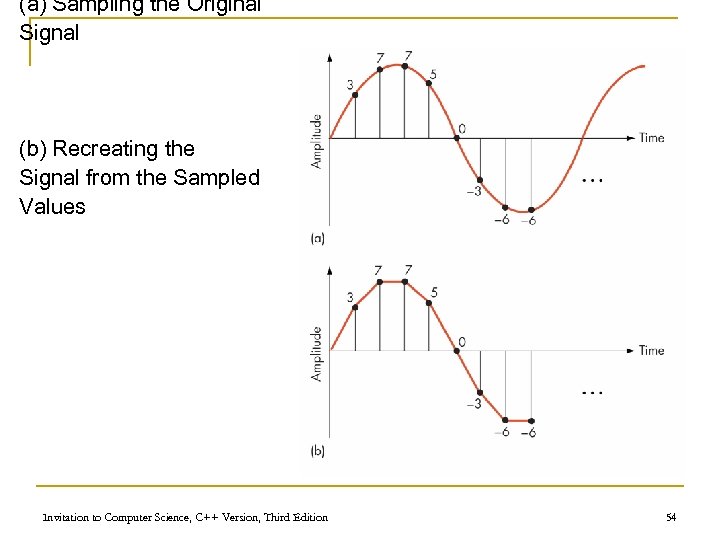
Binary Representation of Sound q q Numbers used to represent the amplitude of sound wave Analog is continuous and we need digital n n n q q Digitize the sound signal Measure the voltage of the signal at certain intervals (40, 000 per sec) Reconstruct wave Digitizing a sound wave Compression can also be used for audio files MP 3: reduces size to 1/10 th n faster transfer over the Internet Invitation to Computer Science, C++ Version, Third Edition 53
(a) Sampling the Original Signal (b) Recreating the Signal from the Sampled Values Invitation to Computer Science, C++ Version, Third Edition 54

Binary Representation of Sound and Images n Storage required n Text – 300 page novel q n Music – WAV q q n 100, 000 words x 5 char/word x 8 bits/char = 4 million bits 44, 100 samp/sec x 16 bits/samp x 60 sec/min = 42 Mbits / min For stereo there are left and right channels => 84 Mbits / min Digital Photo – 3 Megapixel camera, 24 bit color q ≈ 3, 000 pixels/photo x 24 bits/pixel = 72 Mbits = 7 Mbytes Invitation to Computer Science, C++ Version, Third Edition 55

Binary Representation of Sound and Images n Data Compression q Lossless n n q Run-length Encoding (RLE) http: //en. wikipedia. org/wiki/Run-length_encoding Variable length code sets (Huffman code) http: //en. wikipedia. org/wiki/Huffman_coding Lossy n n JPEG – pictures http: //en. wikipedia. org/wiki/JPEG MP 3, ATRAC – audio http: //en. wikipedia. org/wiki/MP 3 Invitation to Computer Science, C++ Version, Third Edition 56

Binary Representation of Sound and Images n Digital image and audio have a lot of advantages over non-digital ones q Can easily be modified by changing the bit pattern n q q q Image enhancement, noise/distortion removal, etc … Superimpose one sound on another or image on another results in newer ones http: //en. wikipedia. org/wiki/Digital_audio_editor http: //en. wikipedia. org/wiki/Video_editing_software Invitation to Computer Science, C++ Version, Third Edition 57

Back To Circuit Design And Construction n Compare-for-equality circuit n Addition circuit n Both circuits can be built using the sum-ofproducts algorithm Invitation to Computer Science, C++ Version, Third Edition 58

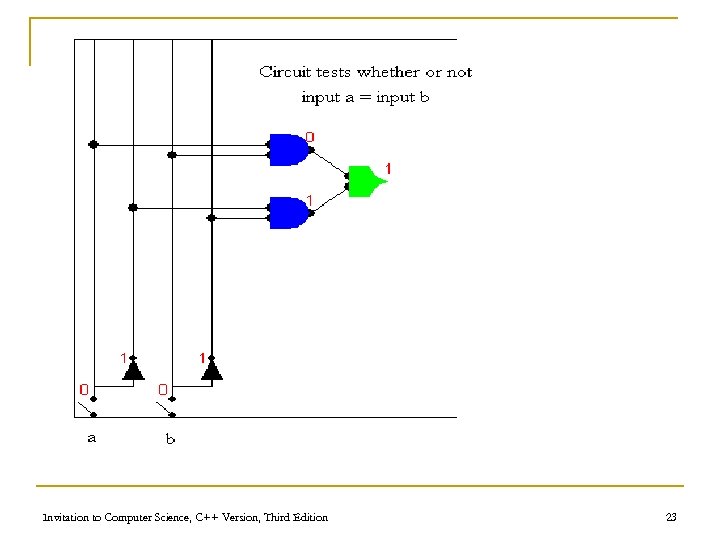
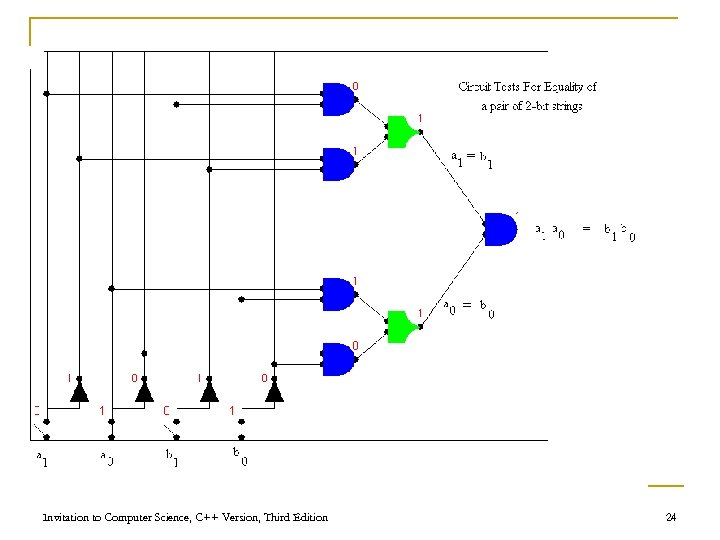
A Compare-for-equality Circuit n Compare-for-equality circuit q q q CE compares two unsigned binary integers for equality Built by combining together 1 -bit comparison circuits (1 -CE) Integers are equal if corresponding bits are equal (AND together 1 -CE circuits for each pair of bits) Invitation to Computer Science, C++ Version, Third Edition 59
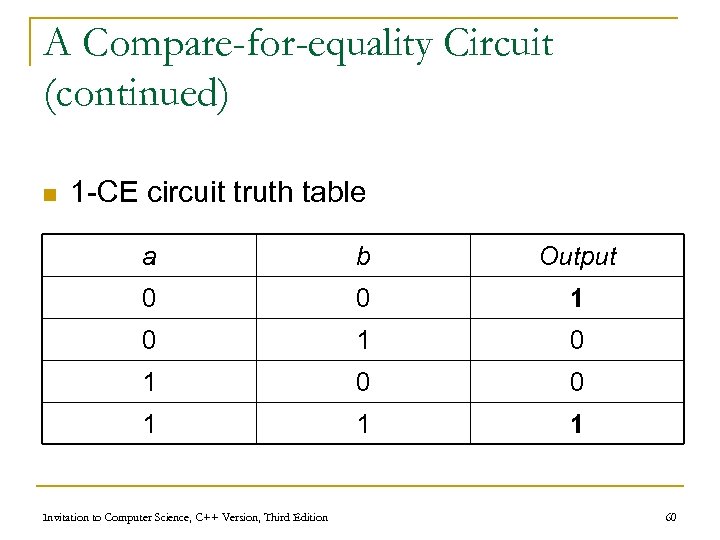
A Compare-for-equality Circuit (continued) n 1 -CE circuit truth table a b Output 0 0 1 0 1 0 0 1 1 1 Invitation to Computer Science, C++ Version, Third Edition 60

A Compare-for-equality Circuit (continued) n 1 -CE Boolean expression q First case: (NOT a) AND (NOT b) q Second case: a AND b q Combined: ((NOT a) AND (NOT b)) OR (a AND b) Invitation to Computer Science, C++ Version, Third Edition 61
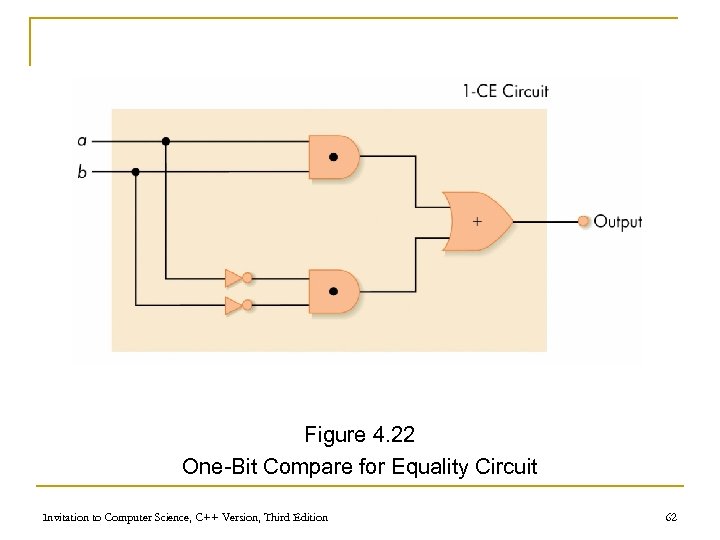
Figure 4. 22 One-Bit Compare for Equality Circuit Invitation to Computer Science, C++ Version, Third Edition 62
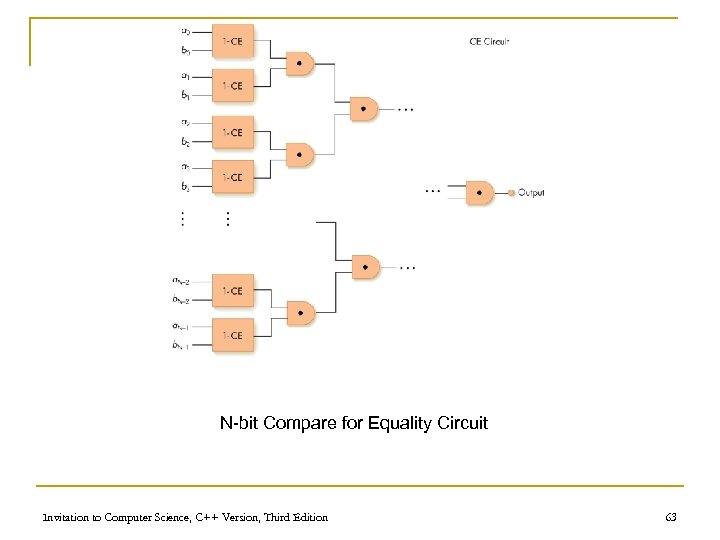
N-bit Compare for Equality Circuit Invitation to Computer Science, C++ Version, Third Edition 63

Binary Addition Invitation to Computer Science, C++ Version, Third Edition 64

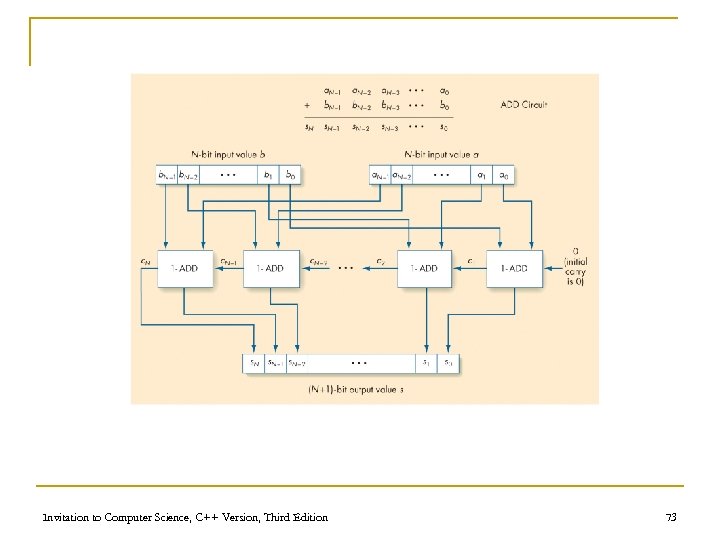
An Addition Circuit n Addition circuit q Adds two unsigned binary integers, setting output bits and an overflow q Built from 1 -bit adders (1 -ADD) q Starting with rightmost bits, each pair produces n A value for that order n A carry bit for next place to the left Invitation to Computer Science, C++ Version, Third Edition 65
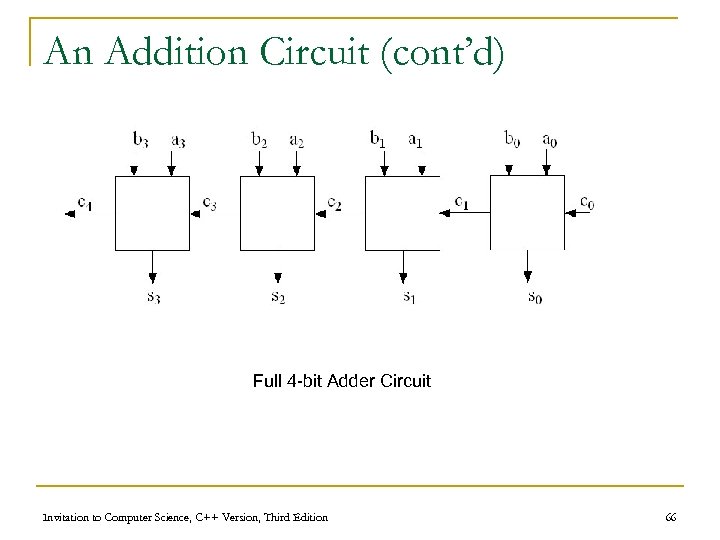
An Addition Circuit (cont’d) Full 4 -bit Adder Circuit Invitation to Computer Science, C++ Version, Third Edition 66

An Addition Circuit (continued) n 1 -ADD truth table q Input n n q One bit from each input integer One carry bit (always zero for rightmost bit) Output n One bit for output place value n One “carry” bit Invitation to Computer Science, C++ Version, Third Edition 67
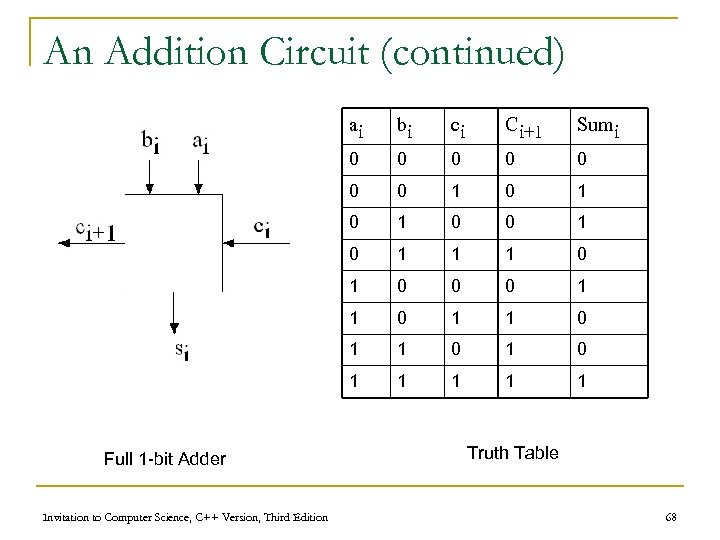
An Addition Circuit (continued) ai Ci+1 Sumi 0 0 0 1 0 1 0 0 1 1 1 0 0 0 1 1 0 1 Invitation to Computer Science, C++ Version, Third Edition ci 0 Full 1 -bit Adder bi 1 1 Truth Table 68
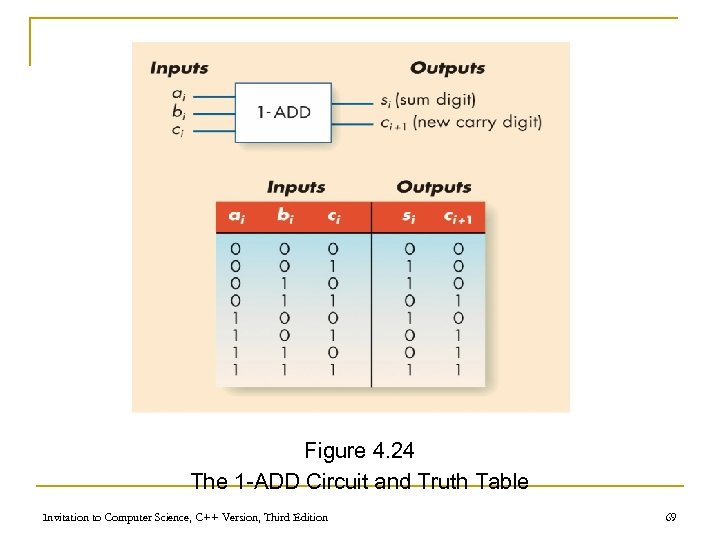
Figure 4. 24 The 1 -ADD Circuit and Truth Table Invitation to Computer Science, C++ Version, Third Edition 69
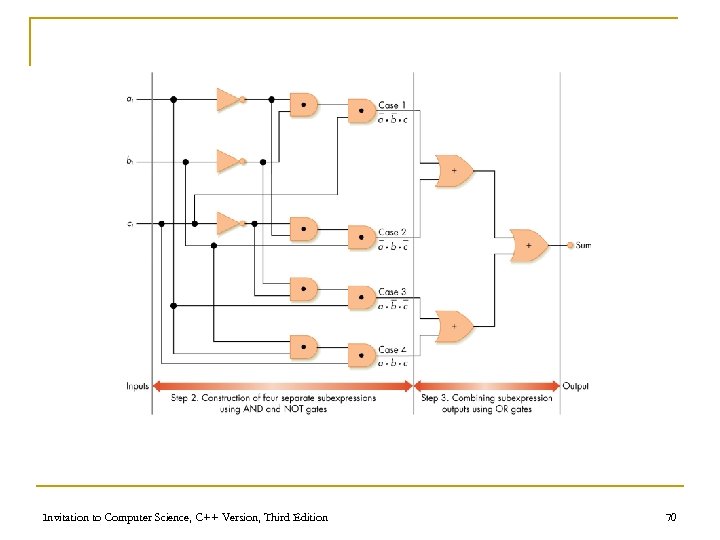
Invitation to Computer Science, C++ Version, Third Edition 70
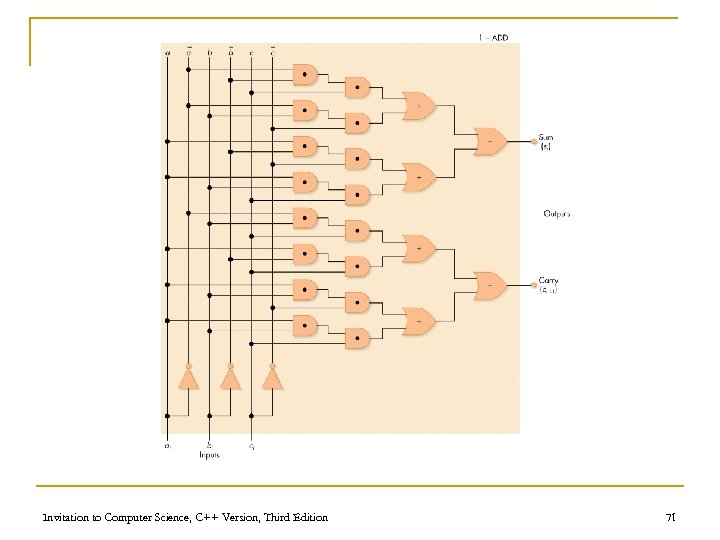
Invitation to Computer Science, C++ Version, Third Edition 71

An Addition Circuit (continued) n Building the full adder q q q Put rightmost bits into 1 -ADD, with zero for the input carry Send 1 -ADD’s output value to output, and put its carry value as input to 1 -ADD for next bits to left Repeat process for all bits Invitation to Computer Science, C++ Version, Third Edition 72
Invitation to Computer Science, C++ Version, Third Edition 73
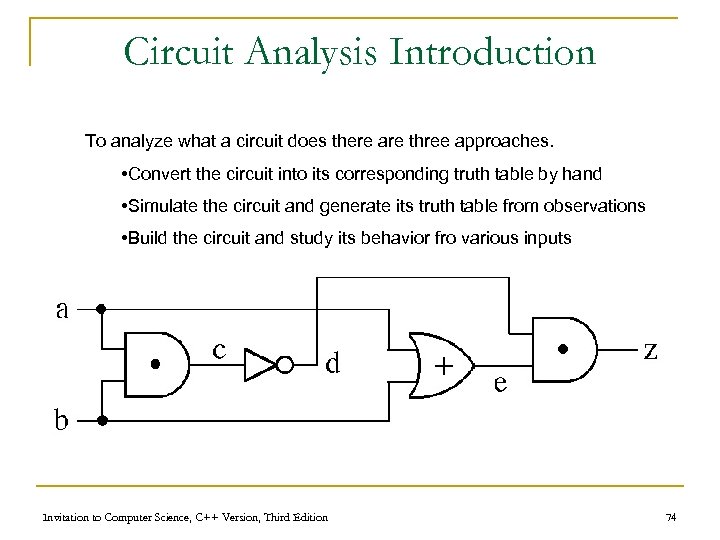
Circuit Analysis Introduction To analyze what a circuit does there are three approaches. • Convert the circuit into its corresponding truth table by hand • Simulate the circuit and generate its truth table from observations • Build the circuit and study its behavior fro various inputs Invitation to Computer Science, C++ Version, Third Edition 74

Circuit Analysis Intro. Cont’d. Generate truth table by hand inputs internal lines Remove Internal Lines Output a b c d e z 0 0 0 1 0 1 1 0 0 1 1 1 0 1 0 Invitation to Computer Science, C++ Version, Third Edition inputs a 0 0 1 1 output b 0 1 z 0 1 1 0 75

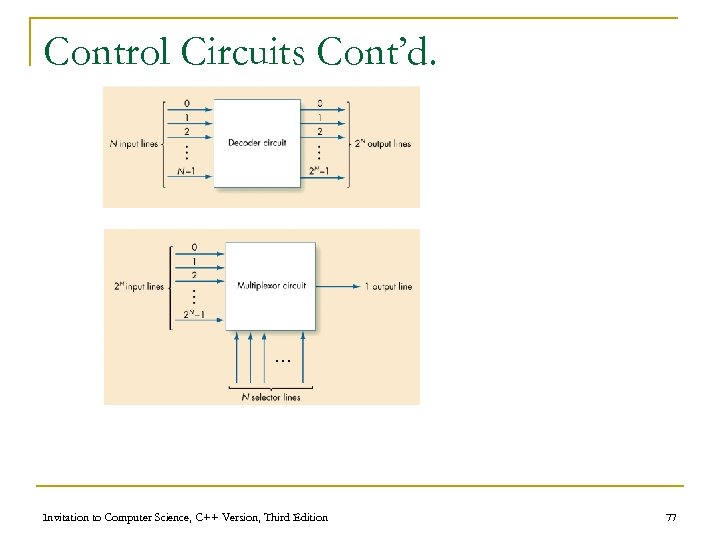
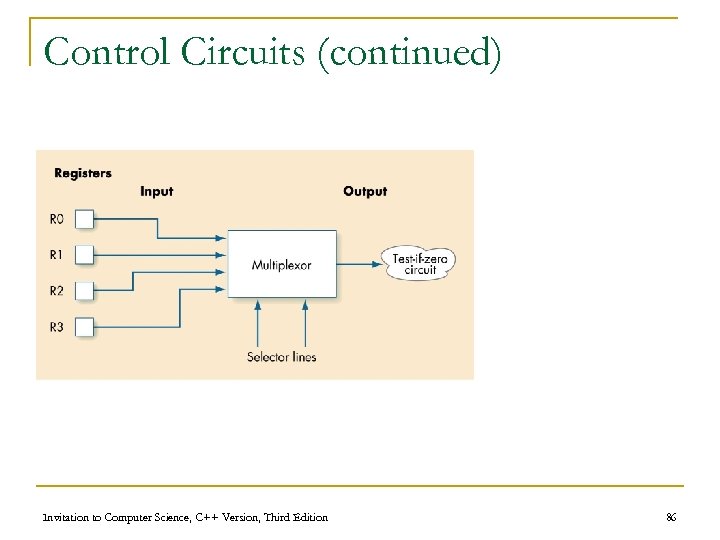
Control Circuits n Do not perform computations n Choose order of operations or select among data values n Major types of controls circuits q Multiplexors n q Select one of inputs to send to output Decoders n Sends a 1 on one output line, based on what input line indicates Invitation to Computer Science, C++ Version, Third Edition 76
Control Circuits Cont’d. Invitation to Computer Science, C++ Version, Third Edition 77

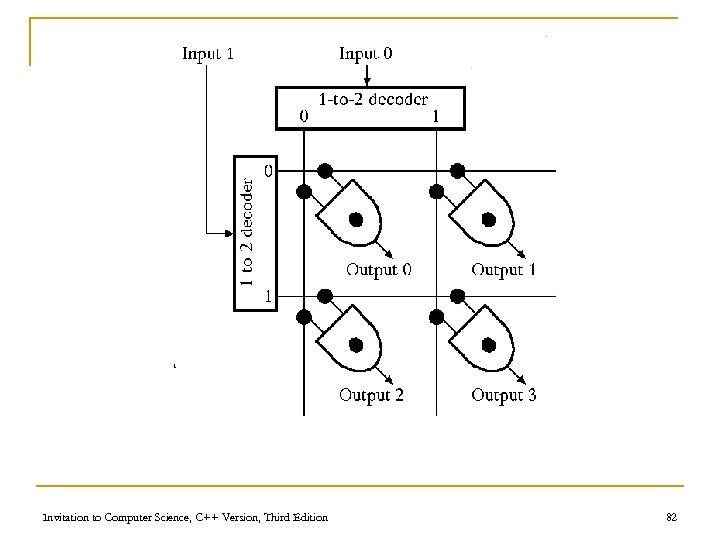
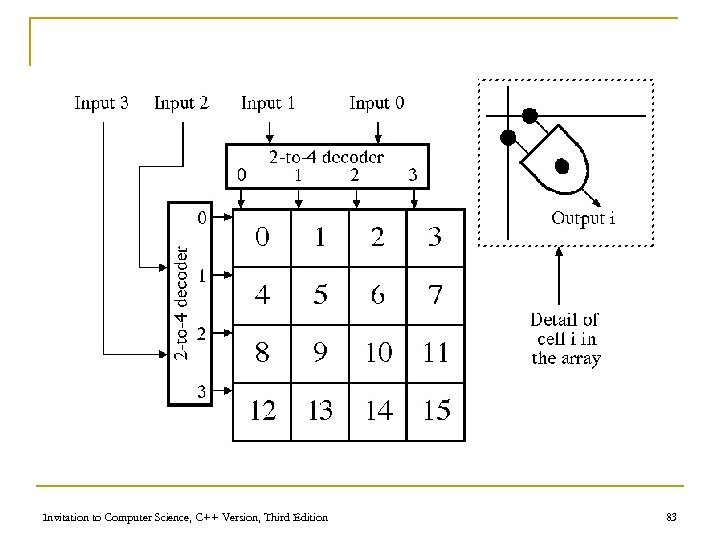
Control Circuits (continued) n Decoder q Form n n q q N input lines 2 N output lines N input lines indicate a binary number, which is used to select one of the output lines Selected output sends a 1, all others send 0 Invitation to Computer Science, C++ Version, Third Edition 78
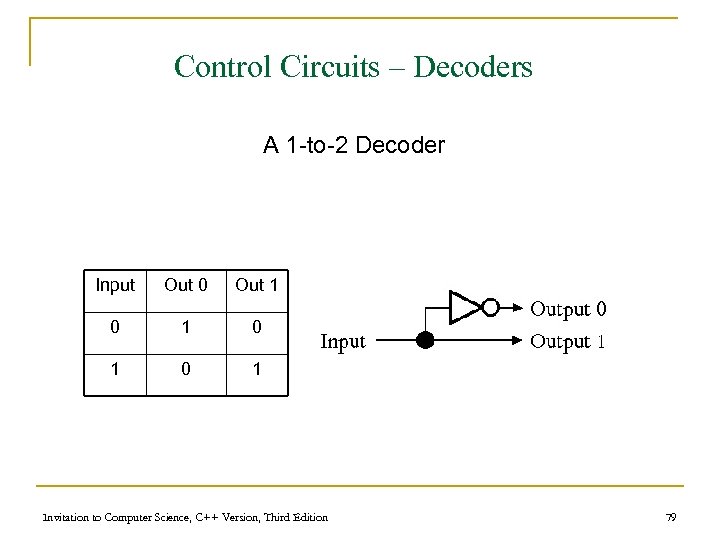
Control Circuits – Decoders A 1 -to-2 Decoder Input Out 0 Out 1 0 1 0 1 Invitation to Computer Science, C++ Version, Third Edition 79

Control Circuits – Decoders Input Lines Output Lines in 1 in 2 out 0 out 1 out 2 out 3 0 0 1 0 0 1 0 0 0 1 A 2 -to-4 Decoder Invitation to Computer Science, C++ Version, Third Edition 80
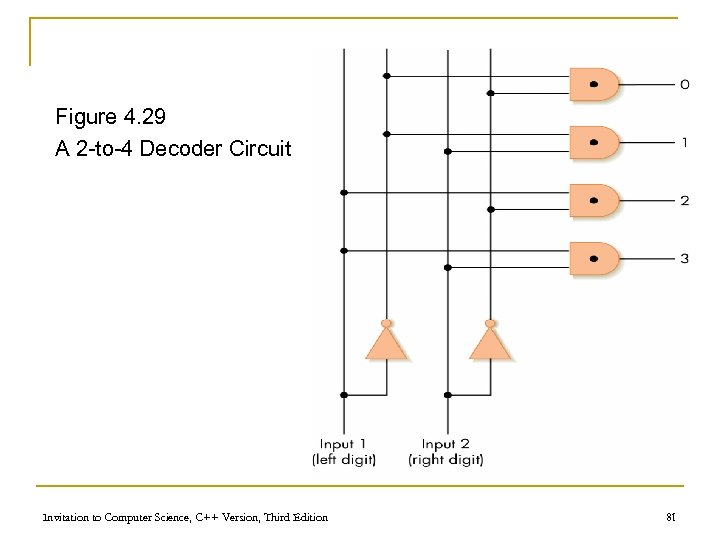
Figure 4. 29 A 2 -to-4 Decoder Circuit Invitation to Computer Science, C++ Version, Third Edition 81
Invitation to Computer Science, C++ Version, Third Edition 82
Invitation to Computer Science, C++ Version, Third Edition 83

Control Circuits (continued) n Decoder purpose q q q Given a number code for some operation, trigger just that operation to take place Numbers might be codes for arithmetic: add, subtract, etc. Decoder signals which operation takes place next Invitation to Computer Science, C++ Version, Third Edition 84

Control Circuits (continued) n Multiplexor form q q N selector input lines q n 2 N regular input lines 1 output line Multiplexor purpose q q Given a code number for some input, selects that input to pass along to its output Used to choose the right input value to send to a computational circuit Invitation to Computer Science, C++ Version, Third Edition 85
Control Circuits (continued) Invitation to Computer Science, C++ Version, Third Edition 86
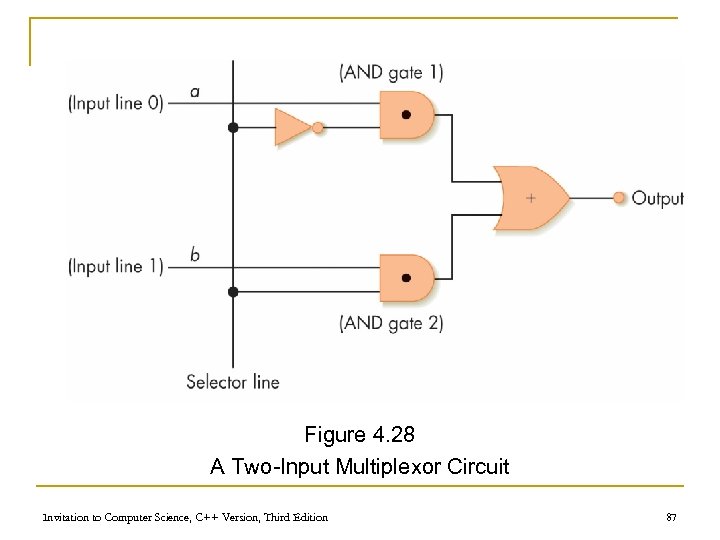
Figure 4. 28 A Two-Input Multiplexor Circuit Invitation to Computer Science, C++ Version, Third Edition 87
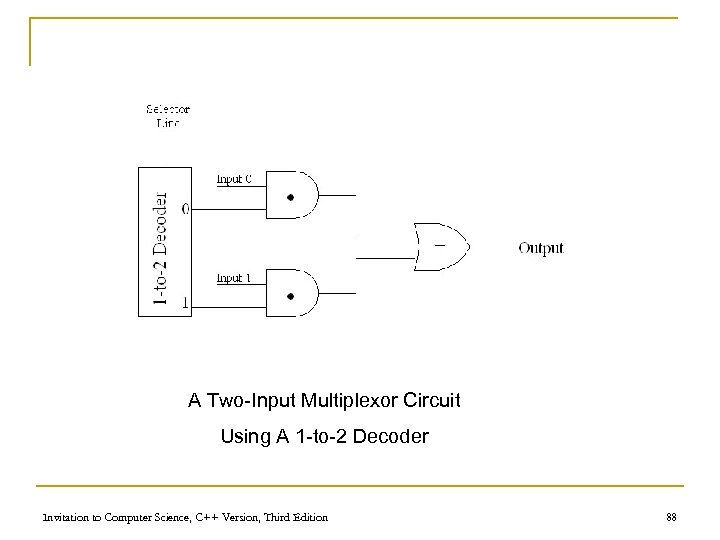
A Two-Input Multiplexor Circuit Using A 1 -to-2 Decoder Invitation to Computer Science, C++ Version, Third Edition 88
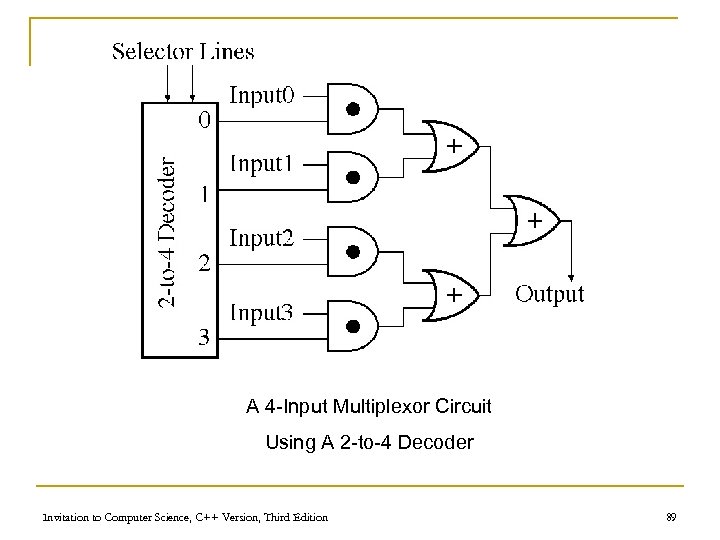
A 4 -Input Multiplexor Circuit Using A 2 -to-4 Decoder Invitation to Computer Science, C++ Version, Third Edition 89
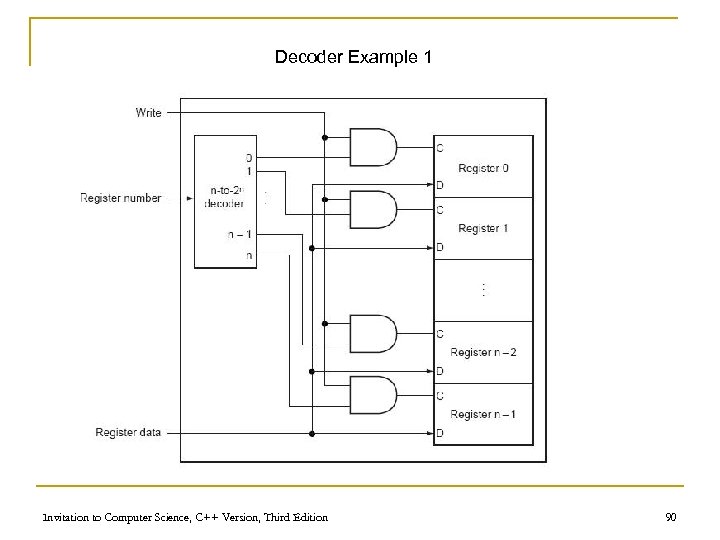
Decoder Example 1 Invitation to Computer Science, C++ Version, Third Edition 90
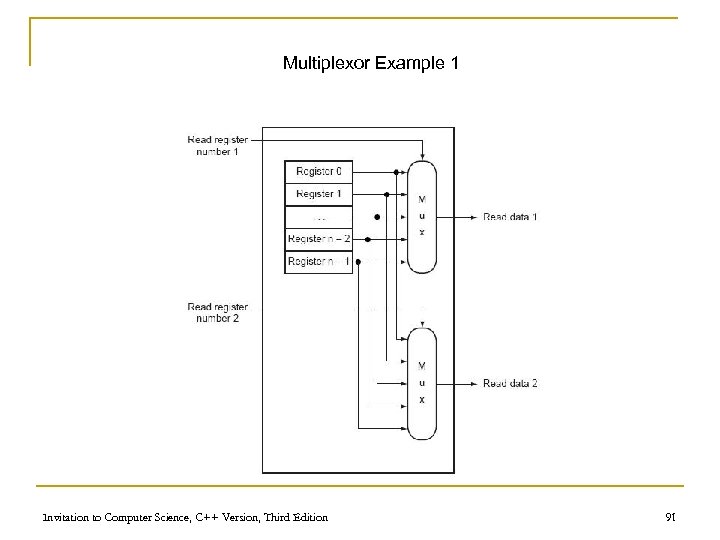
Multiplexor Example 1 Invitation to Computer Science, C++ Version, Third Edition 91

Summary n n n Digital computers use binary representations of data: numbers, text, multimedia Binary values create a bistable environment, making computers reliable Boolean logic maps easily onto electronic hardware Circuits are constructed using Boolean expressions as an abstraction Computational and control circuits may be built from Boolean gates Invitation to Computer Science, C++ Version, Third Edition 92
6d0fce661fc7a9c76be6979dab647c5e.ppt