dadf6a5dd69d009bd899573142a50538.ppt
- Количество слайдов: 56

Chapter 4 Relational Algebra Chapter 5 in Textbook
Database Design Steps in building a database for an application: Real-world domain Relational Algebra Conceptual model DBMS data model Create Schema (DDL) Modify data (DML) 2

Relational Algebra Theoretical expressions where both operands are relations. The output from one operation can become the input to another operation (nested relational algebra). Eight fundamental operations in relational algebra: - Unary operations work on one relation: Selection Projection - Binary operations work on pairs of relations: Cartesian product Join Union Intersection Set difference Division Relational Algebra 3
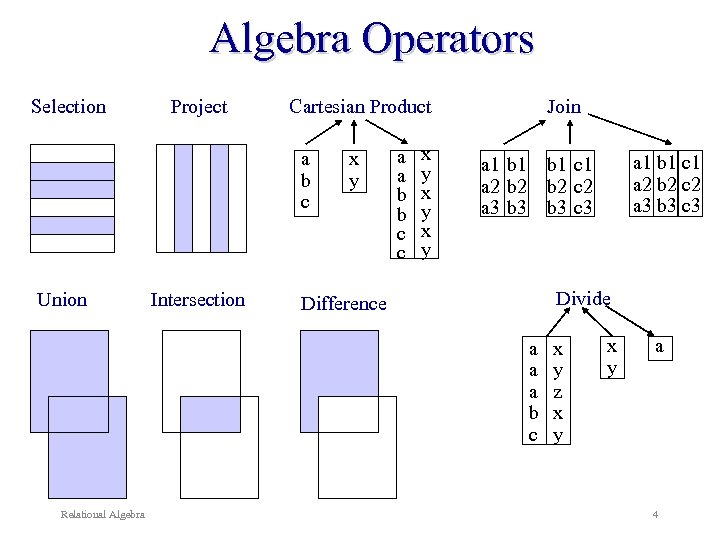
Algebra Operators Selection Project Cartesian Product a b c Union Intersection x y a a b b c c x y x y Join a 1 b 1 a 2 b 2 a 3 b 3 Divide Difference a a a b c Relational Algebra a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 b 1 c 1 b 2 c 2 b 3 c 3 x y z x y a 4

Algebra Operators (Join) T AB a 1 b 2 U B 1 1 3 C x y z Cartesian Product Theta Join A T. B U. B C a 1 1 x a 1 1 y a 1 3 z b 2 1 x b 2 1 y b 2 3 z A T. B U. B C b 2 1 x b 2 1 y Equi. Join Natural Join Outer Join A T. B U. B C a 1 1 x a 1 1 y A B C a 1 x a 1 y A a a b Relational Algebra B C 1 x 1 y 2 Semi. Join A B a 1 5

Selection Operation Return the tuples of R that satisfy a selection condition. Denoted by: <selection condition> (R) Example: Select all staff with a salary greater than 10, 000. salary > 10000 (STAFF) Relational Algebra 6
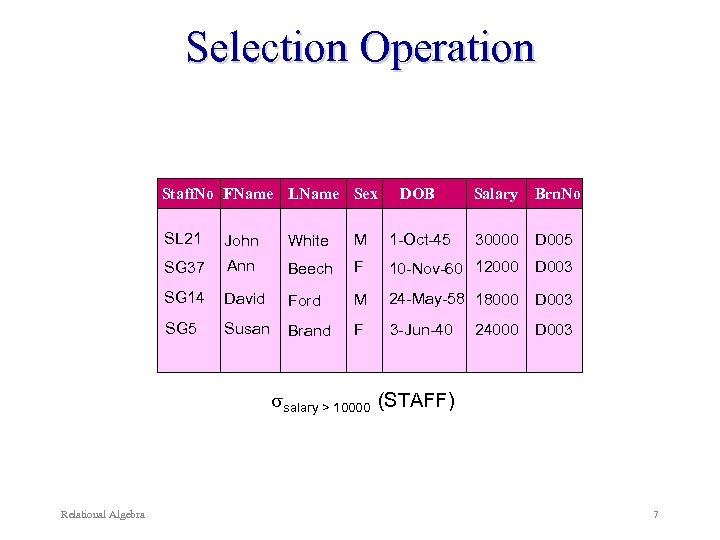
Selection Operation Staff. No FName LName Sex DOB Salary Brn. No SL 21 John White M 1 -Oct-45 SG 37 Ann Beech F 10 -Nov-60 12000 D 003 SG 14 David Ford M 24 -May-58 18000 D 003 SG 5 Susan Brand F 3 -Jun-40 30000 D 005 24000 D 003 salary > 10000 (STAFF) Relational Algebra 7

Projection Operation Return the attributes of R. Denoted by: <attribute list> (R) Example: Produce a list of salaries for all staff, showing only the staff number, first name, last name, and salary. sno, fname, lname, salary(STAFF) Relational Algebra 8
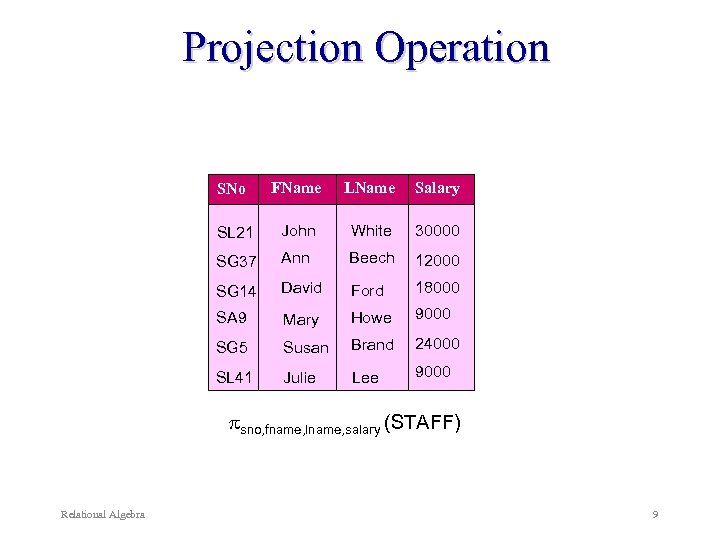
Projection Operation SNo FName LName Salary SL 21 John White 30000 SG 37 Ann Beech 12000 SG 14 David Ford 18000 SA 9 Mary Howe 9000 SG 5 Susan Brand 24000 SL 41 Julie Lee 9000 sno, fname, lname, salary (STAFF) Relational Algebra 9

Question Produce a list of salaries for all staff greater than 10, 000, showing only the staff number, first name, last name, and salary. Relational Algebra 10

Union Operation Return a relation that includes all tuples that are either in R or in S, or in both R and S. Eliminate duplicate tuples. R & S must be union-compatible. Denoted by: R S R a b c Relational Algebra S a d f R S a b c d f 11

Union Operation Example: List all cities where there is either a property for rent. branch office or a city(BRANCH) city(PROPERTY) Relational Algebra 12
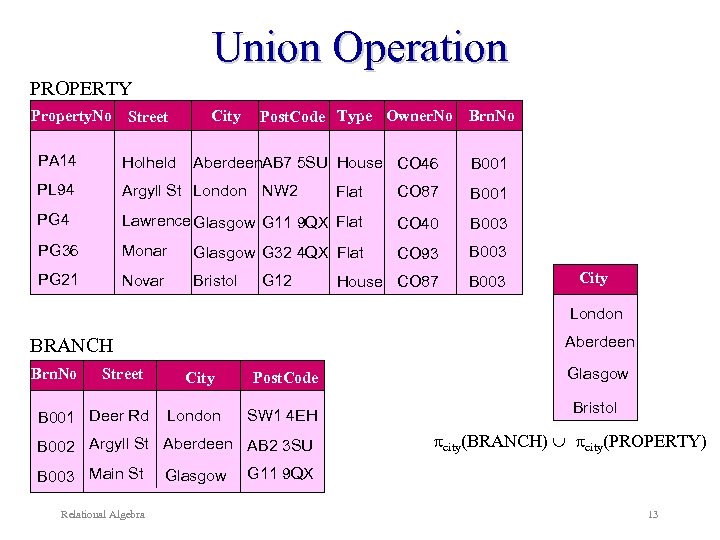
Union Operation PROPERTY Property. No Street City Post. Code Type Owner. No Brn. No PA 14 Holheld PL 94 Argyll St London NW 2 Flat CO 87 B 001 PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 B 003 PG 36 Monar Glasgow G 32 4 QX Flat CO 93 B 003 PG 21 Novar Bristol House CO 87 B 003 Aberdeen. AB 7 5 SU House CO 46 G 12 B 001 City London Aberdeen BRANCH Brn. No Street B 001 Deer Rd City London Post. Code SW 1 4 EH B 002 Argyll St Aberdeen AB 2 3 SU B 003 Main St Relational Algebra Glasgow Bristol city(BRANCH) city(PROPERTY) G 11 9 QX 13

Question List all addresses where there is a branch office or a property for rent in Glasgow city. Relational Algebra 14

Difference Operation Return a relation that includes all tuples that are in R but NOT in S. R & S must be union-compatible. Denoted by: R-S R R-S a b c Relational Algebra S a d f b c 15

Difference Operation Example: List all cities where there is a property for rent but no branch office. city(PROPERTY) - city(BRANCH) Relational Algebra 16
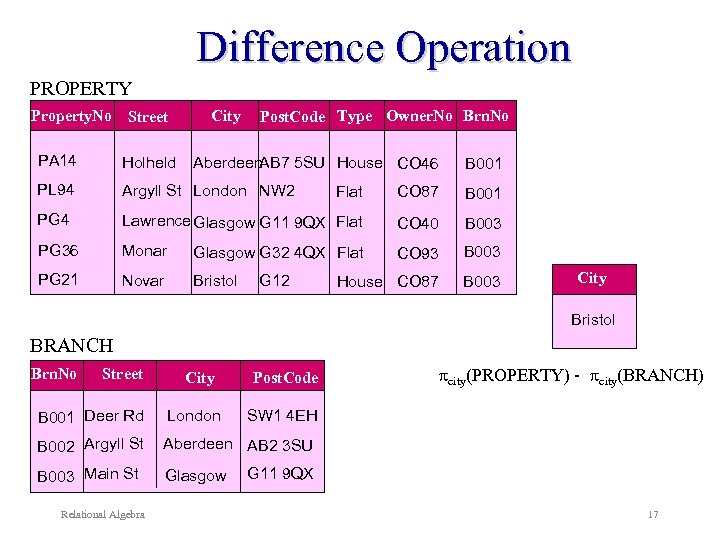
Difference Operation PROPERTY Property. No Street City Post. Code Type Owner. No Brn. No PA 14 Holheld PL 94 Argyll St London NW 2 Flat CO 87 B 001 PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 B 003 PG 36 Monar Glasgow G 32 4 QX Flat CO 93 B 003 PG 21 Novar Bristol House CO 87 B 003 Aberdeen AB 7 5 SU House CO 46 G 12 B 001 City Bristol BRANCH Brn. No Street City Post. Code B 001 Deer Rd London B 002 Argyll St Aberdeen AB 2 3 SU B 003 Main St Glasgow city(PROPERTY) - city(BRANCH) Relational Algebra SW 1 4 EH G 11 9 QX 17

Intersection Operation Return a relation that includes all tuples that are in both R and S. R & S must be union-compatible. Denoted by: R S R R S a b c Relational Algebra S a d f a 18

Intersection Operation Example: List all cities where there is a branch office and at least one property for rent. city(BRANCH) city(PROPERTY) Relational Algebra 19
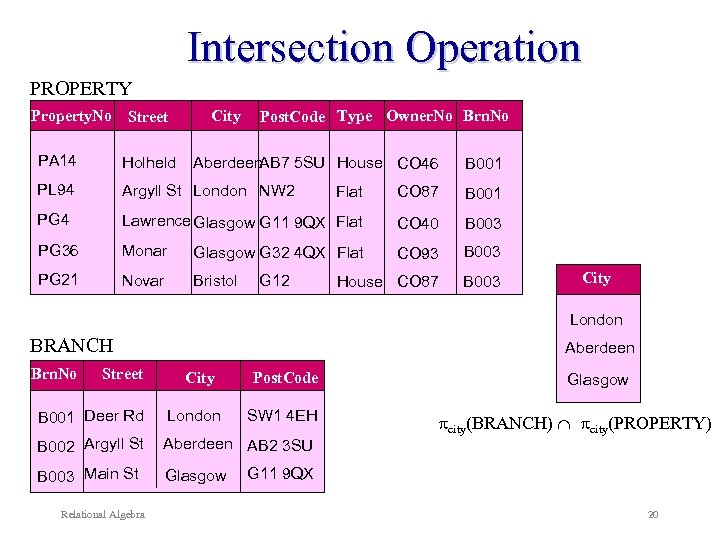
Intersection Operation PROPERTY Property. No Street City Post. Code Type Owner. No Brn. No PA 14 Holheld PL 94 Argyll St London NW 2 Flat CO 87 B 001 PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 B 003 PG 36 Monar Glasgow G 32 4 QX Flat CO 93 B 003 PG 21 Novar Bristol House CO 87 B 003 Aberdeen AB 7 5 SU House CO 46 G 12 B 001 City London BRANCH Brn. No Street Aberdeen City Post. Code B 001 Deer Rd London B 002 Argyll St Aberdeen AB 2 3 SU B 003 Main St Glasgow Relational Algebra SW 1 4 EH Glasgow city(BRANCH) city(PROPERTY) G 11 9 QX 20

Cartesian Product Operation Return a relation that is the concatenation of tuples from two relations R & S. Denoted by: RXS {a, b} X {1, 2, 3} = { (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) } Relational Algebra 21

Cartesian Product Operation Example: List the names and comments of all client who viewed a property. Step 1: Cartesian product Client. No, Fname, Lname (CLIENT) X Client. No, Prprty. No, Comment(VIEW) Client. No, Fname, Lname, View. Client. No, Prprty. No, Comment (CLIENT X VIEW) Step 2: Selection Client. No=View. Client. No( Client. No, Fname, Lname (CLIENT) X Client. No, Prprty. No, Comment(VIEW) ) Relational Algebra 22
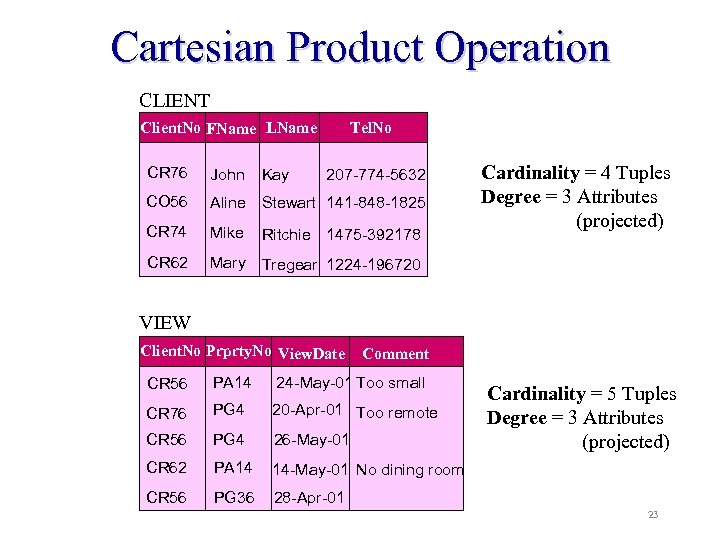
Cartesian Product Operation CLIENT Client. No FName LName Tel. No CR 76 John Kay CO 56 Aline Stewart 141 -848 -1825 CR 74 Mike Ritchie 1475 -392178 CR 62 Mary Cardinality = 4 Tuples Degree = 3 Attributes (projected) Tregear 1224 -196720 207 -774 -5632 VIEW Client. No Prprty. No View. Date Comment CR 56 PA 14 24 -May-01 Too small CR 76 PG 4 20 -Apr-01 Too remote CR 56 PG 4 26 -May-01 CR 62 PA 14 14 -May-01 No dining room CR 56 PG 36 28 -Apr-01 Cardinality = 5 Tuples Degree = 3 Attributes (projected) 23
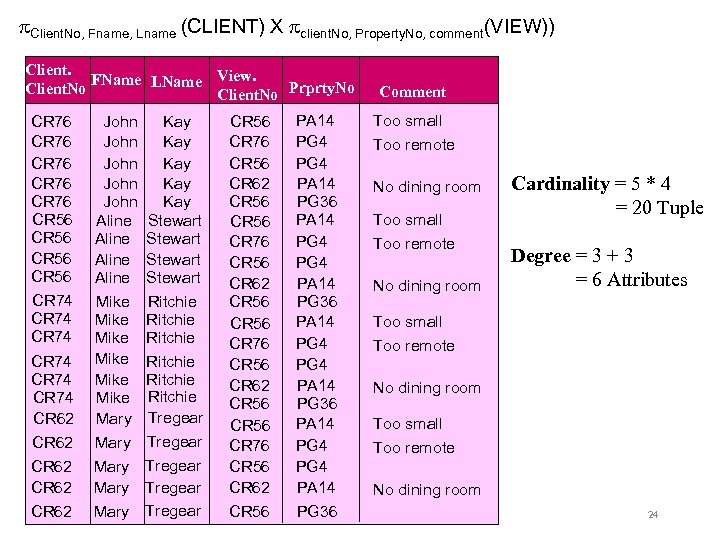
Client. No, Fname, Lname (CLIENT) X client. No, Property. No, comment(VIEW)) Client. FName LName View. Client. No Prprty. No CR 76 CR 76 CR 56 CR 74 CR 74 CR 62 CR 62 John John Aline Mike Mike Mary Mary Kay Kay Kay Stewart Ritchie Ritchie Tregear Tregear CR 56 CR 76 CR 56 CR 62 CR 56 PA 14 PG 4 PG 4 PA 14 PG 36 Comment Too small Too remote No dining room Cardinality = 5 * 4 = 20 Tuple Degree = 3 + 3 = 6 Attributes Too small Too remote No dining room 24
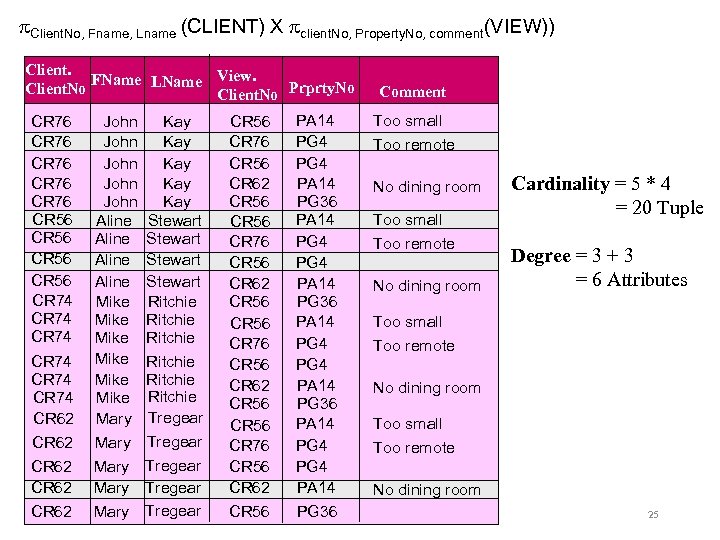
Client. No, Fname, Lname (CLIENT) X client. No, Property. No, comment(VIEW)) Client. FName LName View. Client. No Prprty. No CR 76 CR 76 CR 56 CR 74 CR 74 CR 62 CR 62 John John Aline Mike Mike Mary Mary Kay Kay Kay Stewart Ritchie Ritchie Tregear Tregear CR 56 CR 76 CR 56 CR 62 CR 56 PA 14 PG 4 PG 4 PA 14 PG 36 Comment Too small Too remote No dining room Cardinality = 5 * 4 = 20 Tuple Degree = 3 + 3 = 6 Attributes Too small Too remote No dining room 25
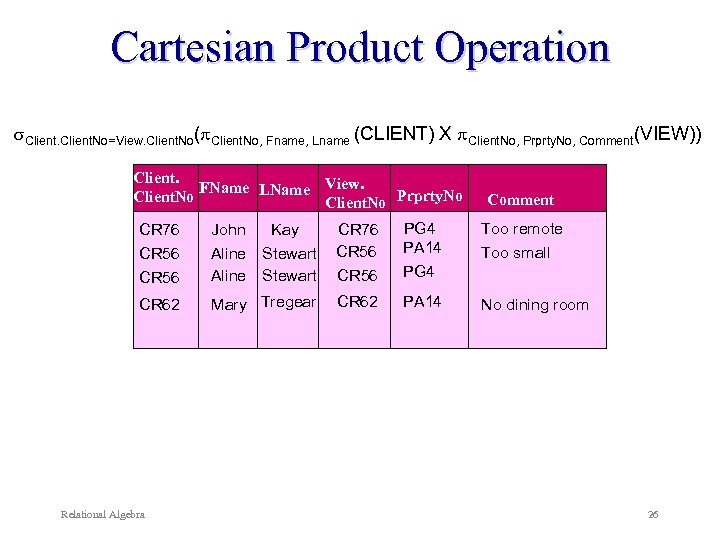
Cartesian Product Operation Client. No=View. Client. No( Client. No, Fname, Lname (CLIENT) X Client. No, Prprty. No, Comment(VIEW)) Client. FName LName View. Client. No Prprty. No CR 76 John Kay CR 56 Aline Stewart CR 62 Mary Tregear Relational Algebra CR 76 CR 56 PG 4 PA 14 CR 56 PG 4 CR 62 PA 14 Comment Too remote Too small No dining room 26

Join Operation Return a relation that is the concatenation of tuples from two relations R & S that satisfy a certain condition. Form of join operation: - Theta join - Equijoin - Natural join - Outer join - Semijoin Relational Algebra 27

Theta join Operation Return a relation that includes all tuples that satisfy the logical condition F from the Cartesian product of R & S. Logical operators ( ) Denoted by: Relational Algebra R F S = F(R X S) 28

Theta join Operation CLIENT(Client. No, FName, Lname, Tel. No) VIEW(Client. No, Property. No, View. Date, Comment) Example: List the names and comments of all renters who have viewed a property. Client. No, Fname, Lname, View. Client. No, Prprty. No, Comment (CLIENT client. Client. No=View. Client. No VIEW) Alternative: Client. No=View. Client. No( Client. No, Fname, Lname (CLIENT) X Client. No, Prprty. No, Comment(VIEW) ) Relational Algebra 29

Equijoin Operation A Theta join where the logical condition is equality (=). Example: List the names and comments of all renters who have viewed a property. Client. No, Fname, Lname, View. Client. No, Prprty. No, Comment (CLIENT Client. No=View. Client. No VIEW) Relational Algebra 30
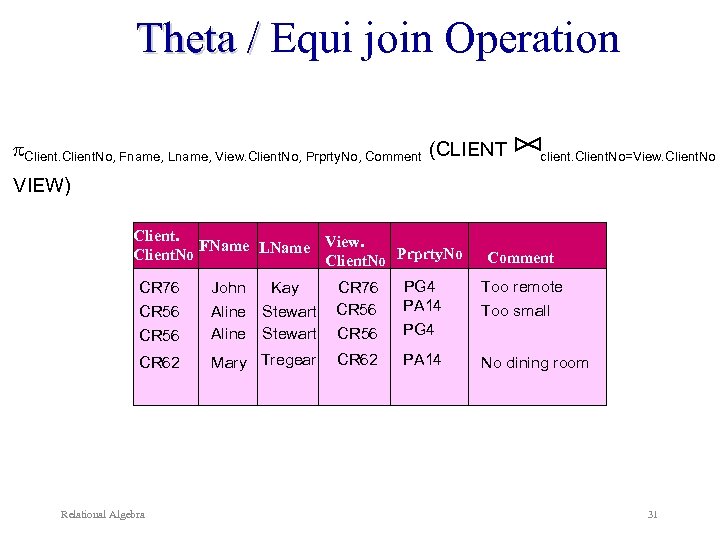
Theta / Equi join Operation Client. No, Fname, Lname, View. Client. No, Prprty. No, Comment (CLIENT client. Client. No=View. Client. No VIEW) Client. FName LName View. Client. No Prprty. No PG 4 PA 14 PG 4 Too remote Stewart CR 76 CR 56 Mary Tregear CR 62 PA 14 No dining room CR 76 John Kay CR 56 Aline CR 62 Relational Algebra Comment Too small 31

Natural join Operation Equijoin of two relation R & S over all common attributes and values. One occurrence of each common attribute is eliminated from the result. Denoted by: R S Example: List the names and comments of all renters who have viewed a property. Client. No, Fname, Lname (CLIENT) Relational Algebra Client. No, Prprty. No, Comment(VIEW) 32
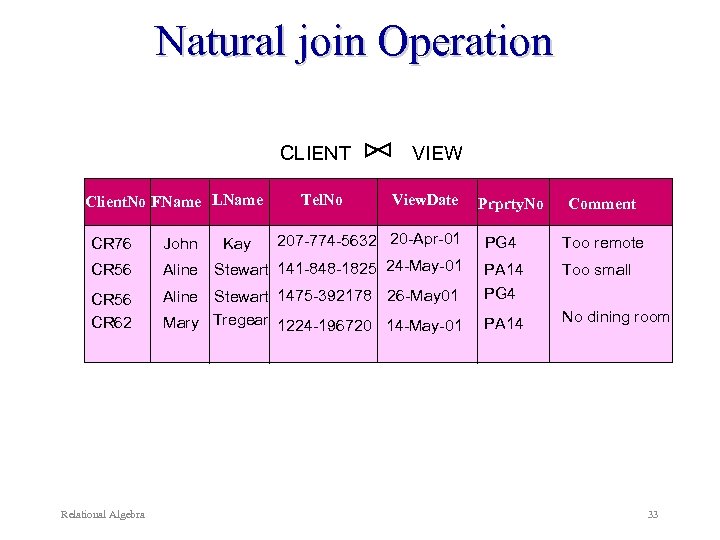
Natural join Operation CLIENT Client. No FName LName CR 76 John CR 56 Aline CR 56 CR 62 Aline Relational Algebra Kay Tel. No VIEW View. Date 207 -774 -5632 20 -Apr-01 Stewart 141 -848 -1825 24 -May-01 Stewart 1475 -392178 26 -May 01 Mary Tregear 1224 -196720 14 -May-01 Prprty. No Comment PG 4 Too remote PA 14 PG 4 Too small PA 14 No dining room 33

Natural join Operation Client. No, Fname, Lname (CLIENT) Client. No, Prprty. No, Comment(VIEW) Client. No FName LName Prprty. No PG 4 Stewart PA 14 Stewart PG 4 CR 76 CR 56 Aline CR 62 Relational Algebra John Kay Mary Tregear PA 14 Comment Too remote Too small No dining room 34

Outer join Operation A natural join in which tuples from R that do not have matching values in the common attributes of S are included in the result relation. Missing values in S are set to null. Denoted by: R S Example: Produce a status report on property viewings. Property. No, Street, City, CLient. No, View. Date, Comment ( PROPERTY Relational Algebra VIEW) 35
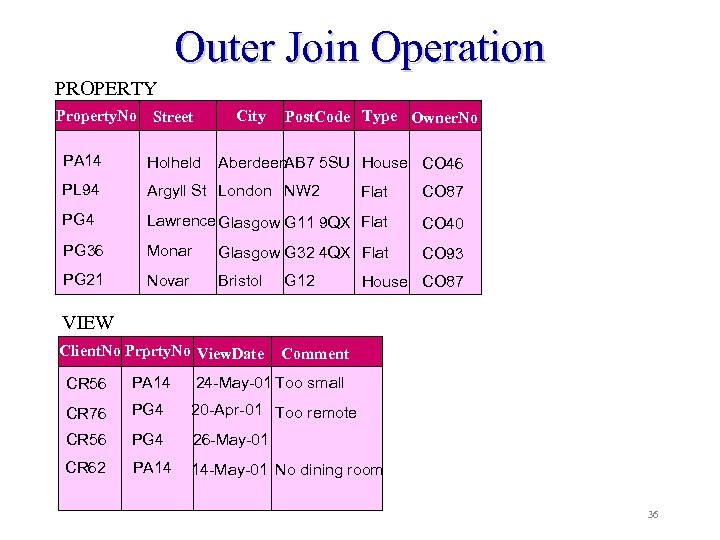
Outer Join Operation PROPERTY Property. No Street City Post. Code Type Owner. No PA 14 Holheld PL 94 Argyll St London NW 2 Flat CO 87 PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 PG 36 Monar Glasgow G 32 4 QX Flat CO 93 PG 21 Novar Bristol Aberdeen AB 7 5 SU House CO 46 G 12 House CO 87 VIEW Client. No Prprty. No View. Date Comment CR 56 PA 14 24 -May-01 Too small CR 76 PG 4 20 -Apr-01 Too remote CR 56 PG 4 26 -May-01 CR 62 PA 14 14 -May-01 No dining room 36
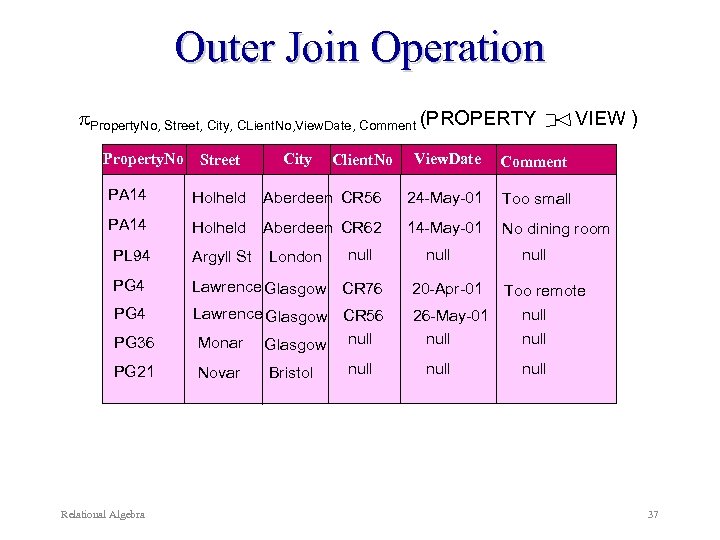
Outer Join Operation Property. No, Street, City, CLient. No, View. Date, Comment (PROPERTY Property. No Street City Client. No View. Date VIEW ) Comment PA 14 Holheld Aberdeen CR 56 24 -May-01 Too small PA 14 Holheld Aberdeen CR 62 14 -May-01 No dining room PL 94 Argyll St PG 4 Lawrence Glasgow CR 76 PG 4 PG 36 Lawrence Glasgow CR 56 Monar Glasgow null PG 21 Novar Relational Algebra London Bristol null 20 -Apr-01 Too remote null 26 -May-01 null 37

Semijoin Operation Defines a relation that contains the tuples of R that participate in the join of R with S. Denoted by: R F S = A (R F S) A is the set of attributes for R Relational Algebra 38

Semijoin Operation Example: List the complete details of all properties who belong at the branch in Glasgow. PROPERTY BRANCH Property. Brn. No=Branch. Brn. No and Branch. city=‘Glasgow’ Alternative: Property. No, Property. Street, Property. City, Property. Postcode, Type, Owner. No, Property. Brn. No (PROPERTY Property. Brn. No=Branch. Brn. No and Branch. city=‘Glasgow’ BRANCH) Relational Algebra 39
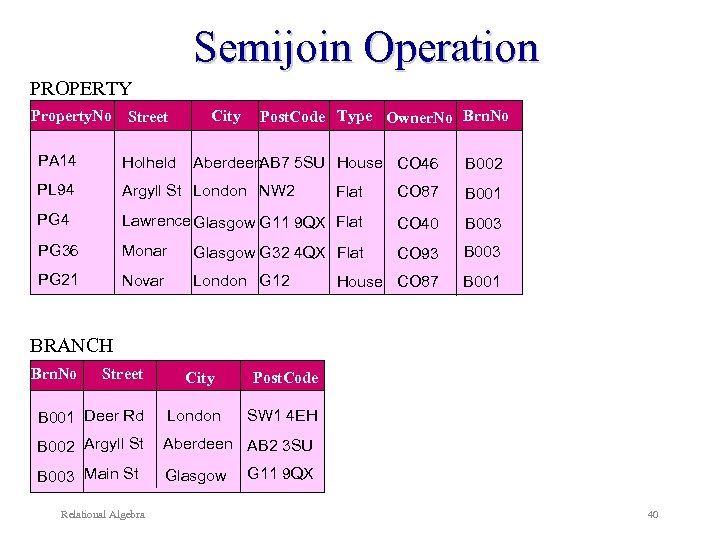
Semijoin Operation PROPERTY Property. No Street City Post. Code Type Owner. No Brn. No PA 14 Holheld PL 94 Argyll St London NW 2 Flat CO 87 B 001 PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 B 003 PG 36 Monar Glasgow G 32 4 QX Flat CO 93 B 003 PG 21 Novar London G 12 House CO 87 B 001 Aberdeen AB 7 5 SU House CO 46 B 002 BRANCH Brn. No Street City Post. Code B 001 Deer Rd London B 002 Argyll St Aberdeen AB 2 3 SU B 003 Main St Glasgow Relational Algebra SW 1 4 EH G 11 9 QX 40
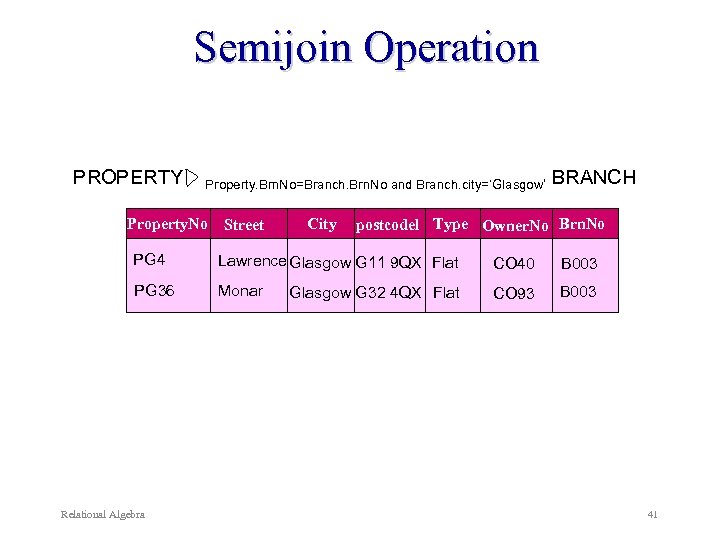
Semijoin Operation PROPERTY Property. Brn. No=Branch. Brn. No and Branch. city=‘Glasgow’ Property. No Street City BRANCH postcodel Type Owner. No Brn. No PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 B 003 PG 36 Monar CO 93 B 003 Relational Algebra Glasgow G 32 4 QX Flat 41

Question List details of branches managing properties of flat type. Relational Algebra 42

Division Operation Assume Relation R defined over attribute set A. Relation S is defined over the attribute set B. B A C = A - B (attributes of R that are not of S) The division operation consists of the set of tuples from R defined over the attributes C that match the combination of every tuple in S. Denoted by: Relational Algebra R S 43

Division Operation Example: Identify all clients who have viewed all properties with three rooms. ( Client. No, Property. No (VIEW)) Relational Algebra ( Property. No ( room=3 (PROPERTY)) ) 44
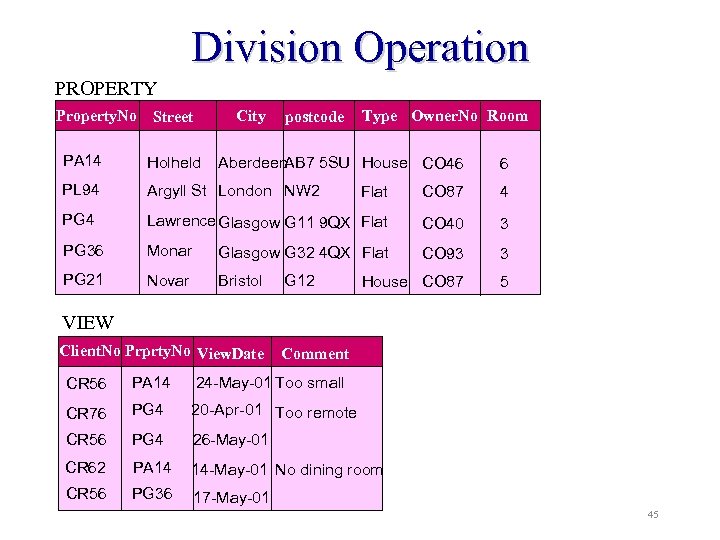
Division Operation PROPERTY Property. No Street City postcode Type Owner. No Room PA 14 Holheld PL 94 Argyll St London NW 2 Flat CO 87 4 PG 4 Lawrence Glasgow G 11 9 QX Flat CO 40 3 PG 36 Monar Glasgow G 32 4 QX Flat CO 93 3 PG 21 Novar Bristol House CO 87 5 Aberdeen AB 7 5 SU House CO 46 G 12 6 VIEW Client. No Prprty. No View. Date Comment CR 56 PA 14 24 -May-01 Too small CR 76 PG 4 20 -Apr-01 Too remote CR 56 PG 4 26 -May-01 CR 62 PA 14 14 -May-01 No dining room CR 56 PG 36 17 -May-01 45
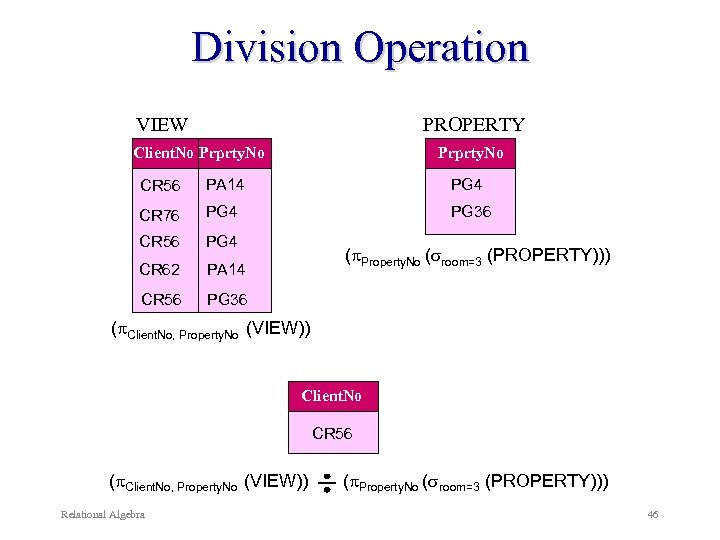
Division Operation VIEW PROPERTY Client. No Prprty. No CR 56 PA 14 PG 4 CR 76 PG 4 PG 36 CR 56 PG 4 CR 62 PA 14 CR 56 PG 36 ( Property. No ( room=3 (PROPERTY))) ( Client. No, Property. No (VIEW)) Client. No CR 56 ( Client. No, Property. No (VIEW)) Relational Algebra ( Property. No ( room=3 (PROPERTY))) 46

Question Identify the clients that has been viewing all properties in Glasgow. Relational Algebra 47

Summary of Relational Algebra Operations Operation Selection Projection Union Difference Intersection Cartesian Product Theta join Equijoin Natural join Outer join Semijoin Division Notation <selection condition>(R) <attribute list>(R) R S R-S R S RXS R FS R S

Review Questions

Review Questions List all employees who works in department number 5. Relational Algebra 50

Review Questions Retrieve the birth date and address of the employee(s) whose name is ‘John B. Smith’. Relational Algebra 51

Review Questions Retrieve all female employees SSN and department name. Relational Algebra 52

Review Questions Retrieve the name and address of all employees who work for the ‘Research’ department. Relational Algebra 53

Review Questions Retrieve the names of employees who have no dependents. Relational Algebra 54

Review Questions List the names of managers who have at least one dependent. Relational Algebra 55

Review Questions Find the names of employees who work on all the projects controlled by department number 5. Relational Algebra 56
dadf6a5dd69d009bd899573142a50538.ppt