Chapter 4 Product and Pricing Strategies for the

Chapter 4 Product and Pricing Strategies for the Multiproduct Monopolist Industrial Organization: Chapter 4 1

Introduction • A monopolist can offer goods of different varieties – multiproduct firms • The “big” issues: – pricing – product variety: how many? – product bundling: • how to bundle • how to price • whether to tie the sales of one product to sales of another • Price discrimination Industrial Organization: Chapter 4 2 4 -1

Price Discrimination • This is a natural phenomenon with multiproduct firms – restaurant meals: table d’hôte or à la carte – different varieties of the same car – airline travel • “goods” of different quality are offered at very different prices • Note the constraints – arbitrage • ensuring that consumers buy the “appropriate” good – identification • How to price goods of different quality? Industrial Organization: Chapter 4 3

Price discrimination and quality • Extract all consumer surplus from the low quality good • Use screening devices – Set the prices of higher quality goods • to meet incentive compatibility constraint • to meet the constraint that higher price is justified by higher quality • One interesting type of screening: crimping the product – offer a product of reasonably high quality – produce lower quality by damaging the higher quality good • student version of Mathematica • different versions of Matlab • the “slow” 486 SX produced by damaging the higher speed 486 DX – why? • for cost reasons Industrial Organization: Chapter 4 4

A Spatial Approach to Product Variety • Approach to product quality in Chapter 3 is an example of vertical product differentiation – products differ in quality – consumers have similar attitudes to quality: value high quality • An alternative approach – consumers differ in their tastes – firm has to decide how best to serve different types of consumer – offer products with different characteristics but similar qualities • This is horizontal product differentiation Industrial Organization: Chapter 4 5

A Spatial Approach to Product Variety (cont. ) • The spatial model (Hotelling) is useful to consider – pricing – design – variety • Has a much richer application as a model of product differentiation – “location” can be thought of in • space (geography) • time (departure times of planes, buses, trains) • product characteristics (design and variety) Industrial Organization: Chapter 4 6

A Spatial Approach to Product Variety (cont. ) • Assume N consumers living equally spaced along Main Street – 1 mile long. • Monopolist must decide how best to supply these consumers • Consumers buy exactly one unit provided that price plus transport costs is less than V. • Consumers incur there-and-back transport costs of t per unit • The monopolist operates one shop – reasonable to expect that this is located at the center of Main Street Industrial Organization: Chapter 4 7

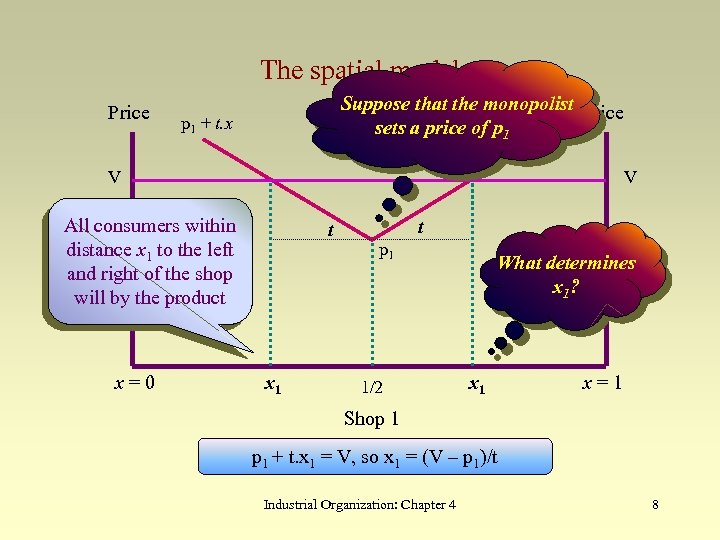The spatial model Price Suppose that the monopolist Price p sets a price of p 1 + t. x 1 p 1 + t. x V V All consumers within distance x 1 to the left and right of the shop will by the product x=0 t x 1 t p 1 1/2 What determines x 1? x 1 x=1 Shop 1 + t. x 1 = V, so x 1 = (V – p 1)/t Industrial Organization: Chapter 4 8

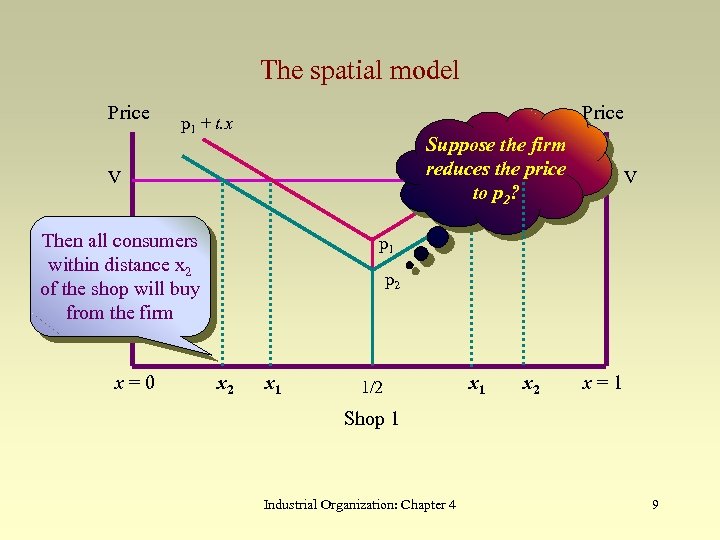The spatial model Price p 1 + t. x Suppose the firm reduces the price to p 2? V Then all consumers within distance x 2 of the shop will buy from the firm x=0 Price V p 1 p 2 x 1 1/2 x 1 x 2 x=1 Shop 1 Industrial Organization: Chapter 4 9

The spatial model • Suppose that all consumers are to be served at price p. – The highest price is that charged to the consumers at the ends of the market – Their transport costs are t/2 : since they travel ½ mile to the shop – So they pay p + t/2 which must be no greater than V. – So p = V – t/2. • Suppose that marginal costs are c per unit. • Suppose also that a shop has set-up costs of F. • Then profit is p(N, 1) = N(V – t/2 – c) – F. Industrial Organization: Chapter 4 10

Monopoly Pricing in the Spatial Model • What if there are two shops? • The monopolist will coordinate prices at the two shops • With identical costs and symmetric locations, these prices will be equal: p 1 = p 2 = p – Where should they be located? – What is the optimal price p*? Industrial Organization: Chapter 4 11

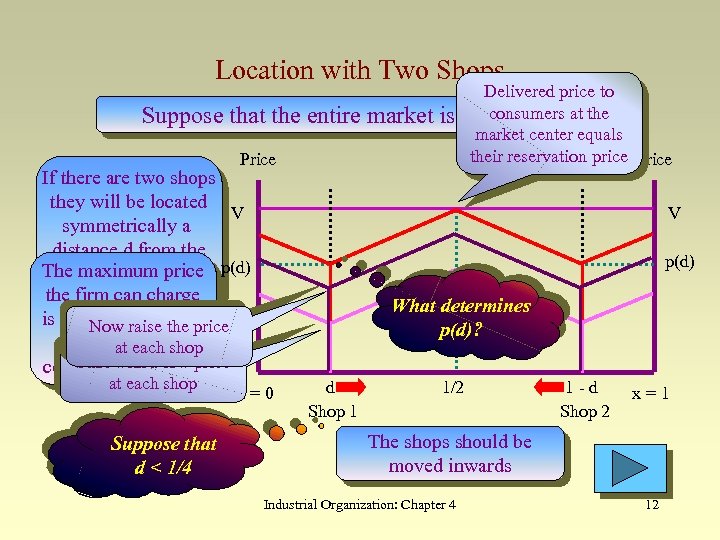Location with Two Shops Suppose that the entire market is Price If there are two shops they will be located V symmetrically a distance d from the The maximum price p(d) end-points of the firm can charge market is determined by the Now raise the price consumers at the at each shop Start with market center of the a low price at each shop Suppose that d < 1/4 Delivered price to consumers at to be served the market center equals their reservation price Price V p(d) What determines p(d)? x=0 d Shop 1 1/2 1 -d Shop 2 x=1 The shops should be moved inwards Industrial Organization: Chapter 4 12

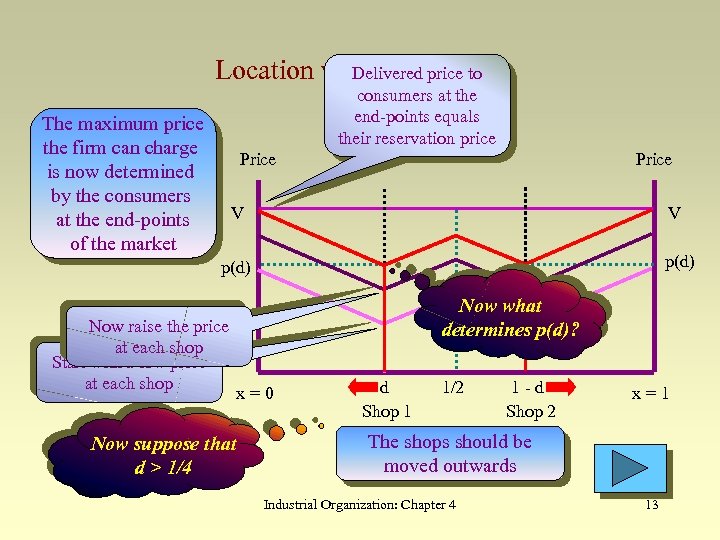Delivered Shops Location with Twoprice to consumers at the end-points equals their reservation price The maximum price the firm can charge is now determined by the consumers at the end-points of the market Price V V p(d) Now raise the price at each shop Start with a low price at each shop Now what determines p(d)? x=0 Now suppose that d > 1/4 d Shop 1 1/2 1 -d Shop 2 x=1 The shops should be moved outwards Industrial Organization: Chapter 4 13

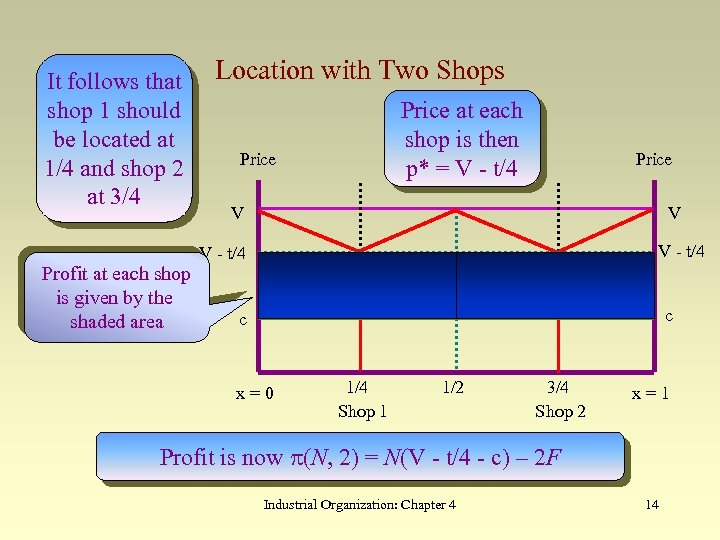It follows that shop 1 should be located at 1/4 and shop 2 at 3/4 Location with Two Shops Price at each shop is then p* = V - t/4 Price V V V - t/4 Profit at each shop is given by the shaded area c c x=0 1/4 Shop 1 1/2 3/4 Shop 2 x=1 Profit is now p(N, 2) = N(V - t/4 - c) – 2 F Industrial Organization: Chapter 4 14

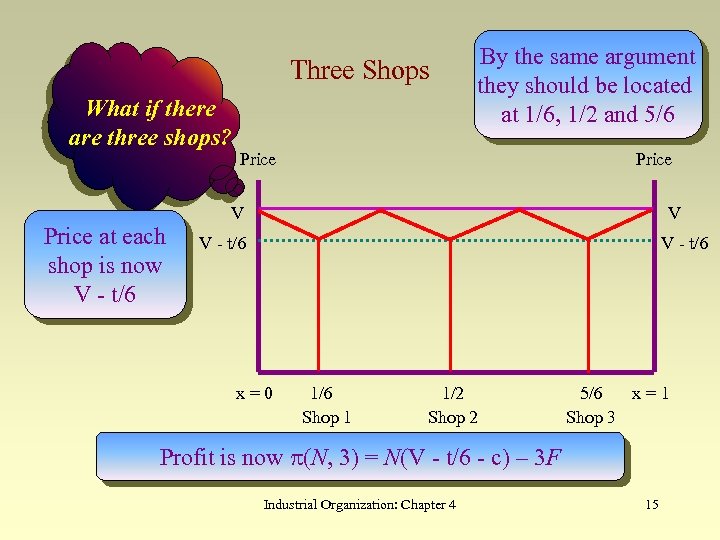Three Shops What if there are three shops? Price at each shop is now V - t/6 By the same argument they should be located at 1/6, 1/2 and 5/6 Price V V V - t/6 x=0 1/6 Shop 1 1/2 Shop 2 5/6 x=1 Shop 3 Profit is now p(N, 3) = N(V - t/6 - c) – 3 F Industrial Organization: Chapter 4 15

Optimal Number of Shops • A consistent pattern is emerging. Assume that there are n shops. They will be symmetrically located distance 1/n apart. We have already considered n = 2 and n = 3. How many shops should When n = 2 we have p(N, 2) = V - t/4 there be? When n = 3 we have p(N, 3) = V - t/6 It follows that p(N, n) = V - t/2 n Aggregate profit is then p(N, n) = N(V - t/2 n - c) – n. F Industrial Organization: Chapter 4 16

Optimal number of shops (cont. ) Profit from n shops is p(N, n) = (V - t/2 n - c)N - n. F and the profit from having n + 1 shops is: p*(N, n+1) = (V - t/2(n + 1)-c)N - (n + 1)F Adding the (n +1)th shop is profitable if p(N, n+1) - p(N, n) > 0 This requires t. N/2 n - t. N/2(n + 1) > F which requires that n(n + 1) < t. N/2 F. Industrial Organization: Chapter 4 17

An example Suppose that F = $50, 000 , N = 5 million and t = $1 Then t. N/2 F = 50 So we need n(n + 1) < 50. This gives n = 6 There should be no more than seven shops in this case: if n = 6 then adding one more shop is profitable. But if n = 7 then adding another shop is unprofitable. Industrial Organization: Chapter 4 18

Some Intuition • What does the condition on n tell us? • Simply, we should expect to find greater product variety when: • there are many consumers. • set-up costs of increasing product variety are low. • consumers have strong preferences over product characteristics and differ in these. Industrial Organization: Chapter 4 19

How Much of the Market to Supply • Should the whole market be served? – Suppose not. Then each shop has a local monopoly – Each shop sells to consumers within distance r – How is r determined? • • • it must be that p + tr = V so r = (V – p)/t so total demand is 2 N(V – p)/t profit to each shop is then p = 2 N(p – c)(V – p)/t – F differentiate with respect to p and set to zero: dp/dp = 2 N(V – 2 p + c)/t = 0 – So the optimal price at each shop is p* = (V + c)/2 – If all consumers are to be served then price is p(N, n) = V – t/2 n • Only part of the market should be served if p(N, n) > p* • This implies that V > c + t/n. Industrial Organization: Chapter 4 20

Partial Market Supply • If c + t/n > V supply only part of the market and set price p* = (V + c)/2 • If c + t/n < V supply the whole market and set price p(N, n) = V – t/2 n • Supply only part of the market: – if the consumer reservation price is low relative to marginal production costs and transport costs – if there are very few outlets Industrial Organization: Chapter 4 21

Are there too many shops or What number of shops maximizes total surplus? too few? Social Optimum Total surplus is consumer surplus profit Consumer surplus is total willingness to pay minus total revenue Profit is total revenue minus total cost Total surplus is then total willingness to pay minus total costs Total willingness to pay by consumers is N. V Total surplus is therefore N. V - Total Cost So what is Total Cost? Industrial Organization: Chapter 4 22

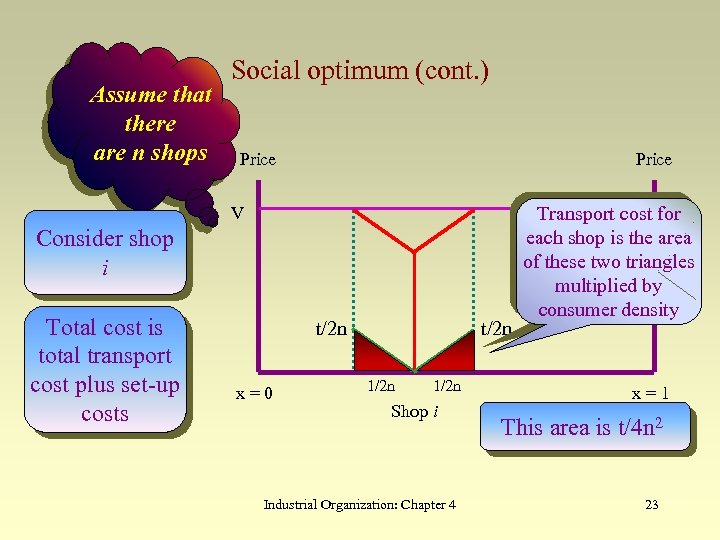Assume that there are n shops Social optimum (cont. ) Price V Consider shop i Total cost is total transport cost plus set-up costs t/2 n x=0 t/2 n 1/2 n Shop i Industrial Organization: Chapter 4 V Transport cost for each shop is the area of these two triangles multiplied by consumer density x=1 This area is t/4 n 2 23

Social optimum (cont. ) Total cost with n shops is, therefore: C(N, n) = n(t/4 n 2)N + n. F = t. N/4 n + n. F If t = $1, F = $50, 000, Total cost with n + 1 shops is: C(N, n+1) = t. N/4(n+1)+fivethis There 5 should be (n+1). F N = million then shops: with. C(N, n adding us n = 4 + tells another Adding another shop is socially efficient ifcondition 1) < C(N, n) shop is efficient that n(n+1) < 25 This requires that t. N/4 n - t. N/4(n+1) > F which implies that n(n + 1) < t. N/4 F The monopolist operates too many shops and, more generally, provides too much product variety Industrial Organization: Chapter 4 24

Monopoly, Product Variety and Price Discrimination • Suppose that the monopolist delivers the product. – then it is possible to price discriminate • What pricing policy to adopt? – – charge every consumer his reservation price V the firm pays the transport costs this is uniform delivered pricing it is discriminatory because price does not reflect costs • Should every consumer be supplied? – – – suppose that there are n shops evenly spaced on Main Street cost to the most distant consumer is c + t/2 n supply this consumer so long as V (revenue) > c + t/2 n This is a weaker condition than without price discrimination. Price discrimination allows more consumers to be served. Industrial Organization: Chapter 4 25

Price Discrimination and Product Variety • How many shops should the monopolist operate now? Suppose that the monopolist has n shops and is supplying the entire market. Total revenue minus production costs is N. V – N. c Total transport costs plus set-up costs is C(N, n)=t. N/4 n + n. F So profit is p(N, n) = N. V – N. c – C(N, n) But then maximizing profit means minimizing C(N, n) The discriminating monopolist operates the socially optimal number of shops. Industrial Organization: Chapter 4 26

Bundling • Firms sell goods as bundles – selling two or more goods in a single package – complete stereo systems – fixed-price meals in restaurants • Firms also use tie-in sales: less restrictive than bundling – tie the sale of one good to the purchase of another – computer printers and printer cartridges – constraining the use of spare parts • Why? • Because it is profitable to do so! Industrial Organization: Chapter 4 27

Bundling: an example How much can • Two television stations offered two old Hollywood films How much can be charged for – Casablanca and Son of Godzilla be If the films are sold charged for • Arbitrage is possible between the stations. Godzilla? separately total Casablanca? • Willingness revenue is $19, 000 to pay is: $7, 000 Willingness to pay for Casablanca Godzilla Station A $8, 000 $2, 500 Station B $7, 000 $2, 500 $3, 000 Industrial Organization: Chapter 4 28

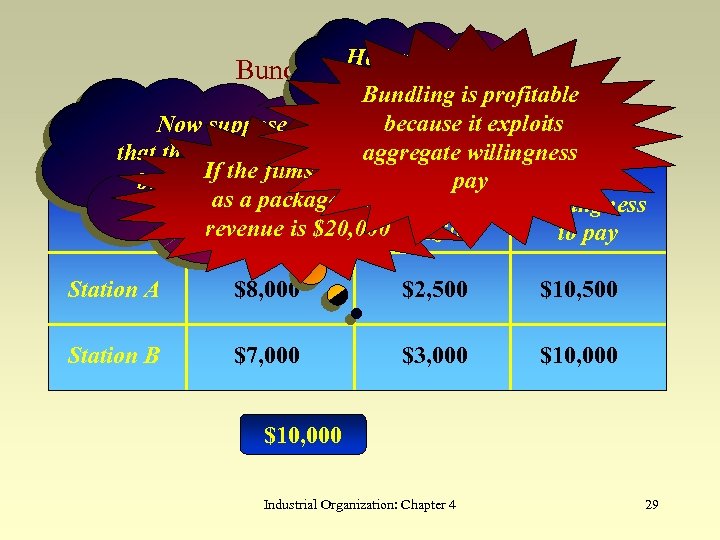How much can be charged is profitable Bundling for thebecause it exploits package? Bundling: an example Now suppose aggregate willingness that the two films are If the sold Willingness to Total pay bundled and films are sold as pay for a package total pay for Willingness as a package revenue is $20, 000 Godzilla Casablanca to pay Station A $8, 000 $2, 500 $10, 500 Station B $7, 000 $3, 000 $10, 000 Industrial Organization: Chapter 4 29

Bundling (cont. ) • Extend this example to allow for – costs – mixed bundling: offering products in a bundle and separately Industrial Organization: Chapter 4 30

Consumer y Each consumer has Bundling: another example py 1 reservation price the firm Supposebuys exactly one that Suppose that there. All consumers in are for good 1 and consumers in sets All py 2 1 for price p region B buy two goods and that unit of p for good and price a good region A buy good 1 2 R 2 only good 2 2 consumers differ in Consumer x has good 2 that price provided for both goods reservation price px 1 less than her their reservation prices A B is for good 1 and px 2 for these goods reservation price for good Allyconsumers in 2 All consumers in py 2 region C buy region D buy p 2 Consumers x neither good only good 1 px 2 split into four groups D C px 1 py 1 Industrial Organization: Chapter 4 R 1 31

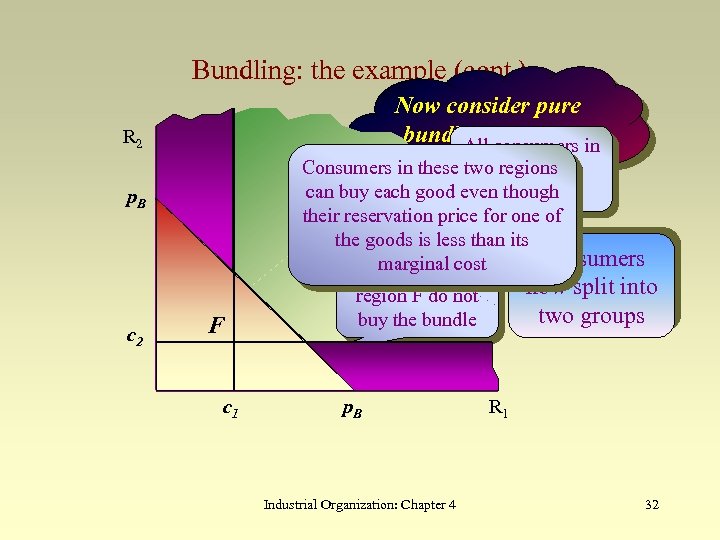Bundling: the example (cont. ) Now consider pure bundling consumers in at some All price p. B E buy Consumers in these two regions region R 2 can buy each good even though the bundle their reservation price for one of Ethe goods is less than its Consumers All marginal cost consumers in p. B c 2 F c 1 now split into two groups region F do not buy the bundle p. B Industrial Organization: Chapter 4 R 1 32

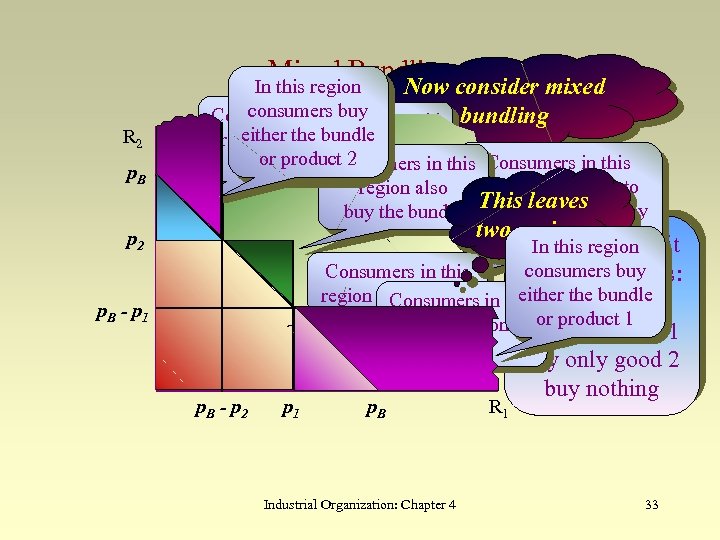Mixed Bundling In this region R 2 p. B p 2 p. B - p 1 Now consider mixed consumers buy Consumers in Good 1 is sold bundling this either the bundle region buy only price p at 1 or product 2 good 2 Consumers in this 2 is sold Good Consumers in this region also at price p are willing to This 2 leaves buy the bundle buy both goods. They two regions buy the bundle Consumers split In this region consumers buy Consumers in this into four groups: either the bundle region buy nothing in thisbuy the bundle Consumers The bundle is sold region < p only or product 1 at price p. Bbuy 1 + pbuy only good 1 2 good 1 p. B - p 2 p 1 p. B Industrial Organization: Chapter 4 R 1 buy only good 2 buy nothing 33

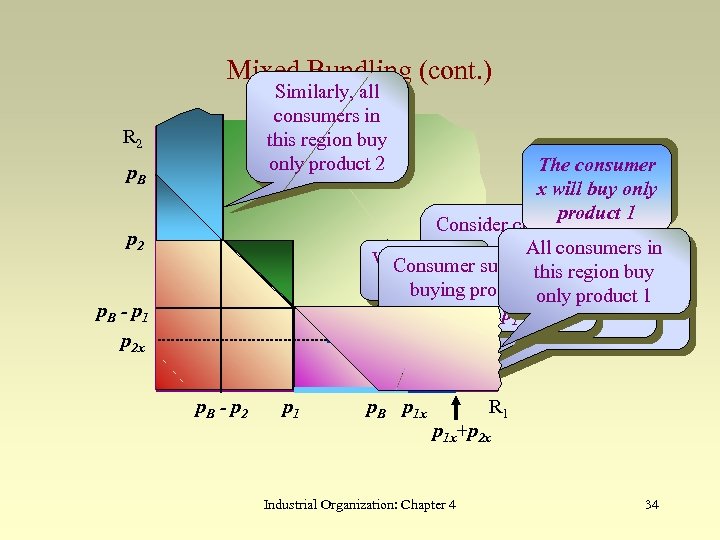Mixed Bundling (cont. ) Similarly, all consumers in this region buy only product 2 R 2 The consumer x will buy only product 1 Consider consumer x with All consumers reservation prices p for in Which is this surplus from 1 x Consumerthis region buy surplus from product 1 and p 2 x for measure Her aggregate willingness buying theis 2 product 1 product only 1 bundle is product to pay for bundle is p 1 x -pp 1 + p thep - B 1 x 2 x p 1 x + p 2 x x p. B p 2 p. B - p 1 p 2 x p. B - p 2 p 1 p. B p 1 x R 1 p 1 x+p 2 x Industrial Organization: Chapter 4 34

Mixed Bundling (cont. ) • What should a firm actually do? • There is no simple answer – mixed bundling is generally better than pure bundling – but bundling is not always the best strategy • Each case needs to be worked out on its merits Industrial Organization: Chapter 4 35

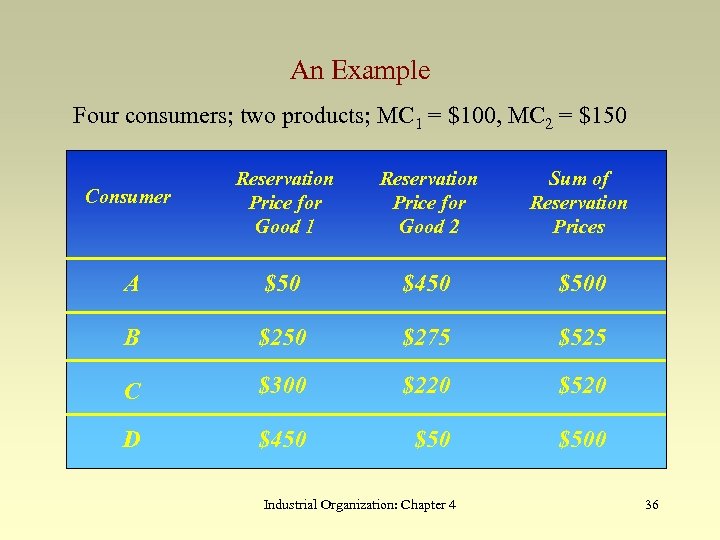An Example Four consumers; two products; MC 1 = $100, MC 2 = $150 Consumer Reservation Price for Good 1 Reservation Price for Good 2 Sum of Reservation Prices A $50 $450 $500 B $250 $275 $525 C $300 $220 $520 D $450 $500 Industrial Organization: Chapter 4 36

The example (cont. ) Good 1: Marginal Cost $100 Price $450 $300 $250 $50 Price $450 $275 $220 $50 Consider Quantity Total revenue simple Profit monopoly pricing 1 $450 $350 2 $400 $600 Good 1 should be sold 3 $750 $450 at $250 and good 2 at 4 $200 -$200 $450. Total profit Good 2: Marginal Cost + $300 is $450 $150 Quantity =Total revenue $750 1 2 3 4 $450 $550 $660 $200 Industrial Organization: Chapter 4 Profit $300 $210 -$400 37

The example (cont. ) Now consider pure bundling Consumer A B C D Reservation Price for. The highest for Price bundle Good 1 price that can be Good 2 considered is $500 All four consumers$450 buy will $50 the bundle and profit is 4 x$500 - 4 x($150 + $100) $250 $275 = $1, 000 $300 $220 $450 $50 Industrial Organization: Chapter 4 Sum of Reservation Prices $500 $525 $520 $500 38

The example (cont. ) Now consider mixed Take the monopoly prices p 1 = $250; p 2 = $450 and a bundle price p. B = $500 bundling All four consumers buy something and profit is Reservation Sum of Consumer Price for Reservation $250 x 2 + $150 x 2 Can the seller improve Price for Good 1 Good 2 Prices = $800 on this? A $50 $450 $500 B $250 $275 $500 $525 C $250 $300 $220 $520 D $250 $450 $500 Industrial Organization: Chapter 4 39

The example (cont. ) Try instead the prices p 1 = $450; p 2 = $450 and a bundle price p. B = $520 This is actually the that the Reservation All four consumers buy best Reservation Consumer Price for Price and profit is $300 + firm can do for Good 1 $270 x 2 + $350 = $1, 190 A $50 Good 2 Sum of Reservation Prices $450 $500 B $250 $275 $520 $525 C $300 $220 $520 D $450 $500 Industrial Organization: Chapter 4 40

Bundling (cont. ) • Bundling does not always work • Requires that there are reasonably large differences in consumer valuations of the goods • What about tie-in sales? – “like” bundling but proportions vary – allows the monopolist to make supernormal profits on the tied good – different users charged different effective prices depending upon usage – facilitates price discrimination by making buyers reveal their demands Industrial Organization: Chapter 4 41

Tie-in Sales • Suppose that a firm offers a specialized product – a camera? – that uses highly specialized film cartridges • Then it has effectively tied the sales of film cartridges to the purchase of the camera – this is actually what has happened with computer printers and ink cartridges • How should it price the camera and film? – suppose that marginal costs of the film and of making the camera are zero (to keep things simple) – suppose also that there are two types of consumer: high-demand low-demand Industrial Organization: Chapter 4 42

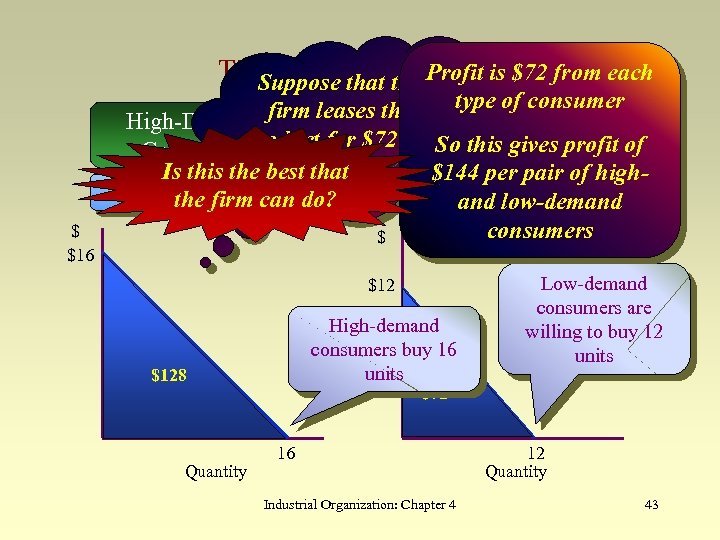Tie-In Sales: anthe Profit is $72 from each Suppose that Example $ $16 type of consumer firm leases the Low-Demand High-Demand product for $72 per. So this gives profit of Consumers Is this the best period that $144 per pair of high. Demand: P firm-can do? Demand: low-demand the = 16 Q and P = 12 - Q consumers $ $12 High-demand consumers buy 16 units $128 Quantity Low-demand consumers are willing to buy 12 units $72 16 Industrial Organization: Chapter 4 12 Quantity 43

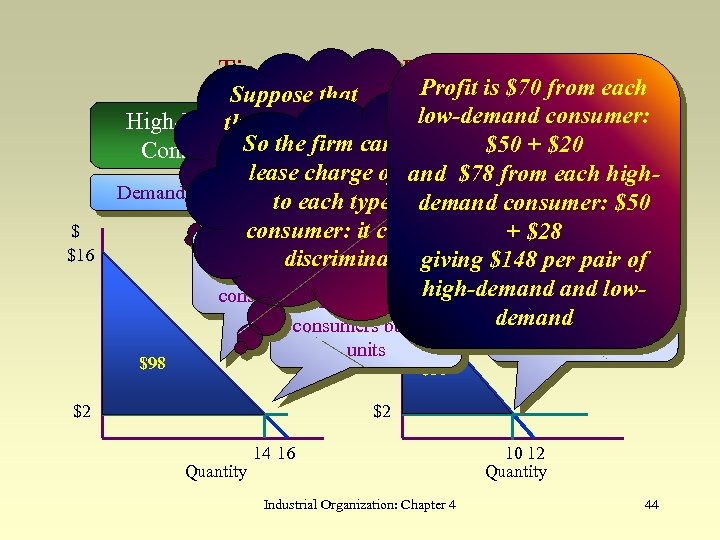Tie-In Sales: an Example $ $16 Profit is $70 from each Suppose that low-demand consumer: High-Demandfirm sets a Low-Demand the So $50 + $20 Consumers the$2 per price of firm can set a Consumers lease charge of $50 $78 from each highand unit Demand: P = 16 - Q each type of Demand: P = 12 - Q Consumer surplus to demand consumer: $50 consumer: it cannot for low-demand + $28 $ Consumer surplus consumers is $50 discriminate giving $148 per pair of for high-demand $12 high-demand lowconsumers is $98 Low-demand High-demand buy 10 consumers buy 14 units $98 $2 units $50 $2 Quantity 14 16 Industrial Organization: Chapter 4 10 12 Quantity 44

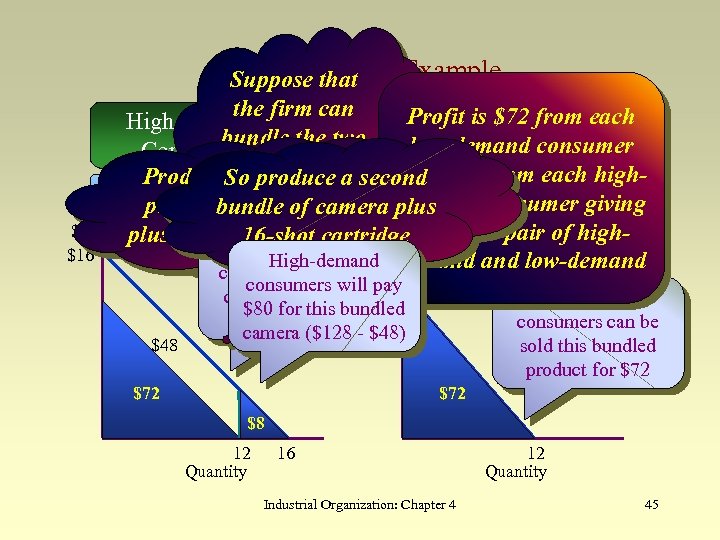Tie-In Sales: an Example Suppose that $ $16 the firm can Profit is $72 from each High-Demand Low-Demand bundle the two low-demand consumer Consumers goods instead and Produce. Sobundled a second $80 from each higha produce Demand: P = 16 - Q them Demand: P = 12 of tieof camera plus demand consumer. Q giving product of camera bundle plus 12 -shot cartridge $ $150 per pair of high 16 -shot cartridge High-demand low-demand consumers get $48 consumers will$12 pay consumer surplus $80 for this bundled from buying it camera ($128 - $48) $72 Low-demand consumers can be sold this bundled product for $72 $8 12 Quantity 16 Industrial Organization: Chapter 4 12 Quantity 45

Complementary Goods • Complementary goods are goods that are consumed together – nuts and bolts – PC monitors and computer processors • How should these goods be produced? • How should they be priced? • Take the example of nuts and bolts – these are perfect complements: need one of each! • Assume that demand for nut/bolt pairs is: Q = A - (PB + PN) Industrial Organization: Chapter 4 46

Complementary goods (cont. ) This demand curve can be written individually for nuts and bolts For bolts: QB = A - (PB + PN) For nuts: QN = A - (PB + PN) These give the inverse demands: PB = (A - PN) - QB PN = (A - PB) - QN These allow us to calculate profit maximizing prices Assume that nuts and bolts are produced by independent firms Each sets MR = MC to maximize profits MRB = (A - PN) - 2 QB MRN = (A - PB) - 2 QN Assume MCB = MCN = 0 Industrial Organization: Chapter 4 47

Complementary goods (cont. ) Therefore QB = (A - PN)/2 and PB = (A - PN) - QB = (A - PN)/2 by a symmetric argument PN = (A - PB)/2 The price set by each firm is affected by the price set by the other firm In equilibrium the price set by the two firms must be consistent Industrial Organization: Chapter 4 48

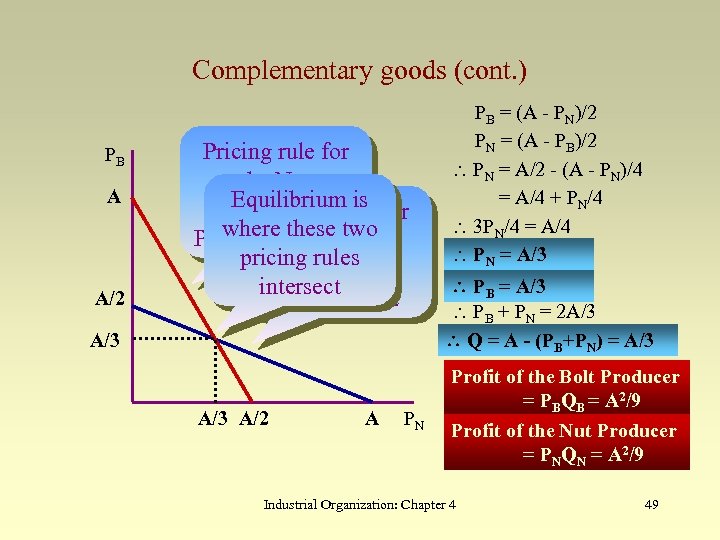Complementary goods (cont. ) PB A A/2 Pricing rule for the Nut Equilibrium is Producer: rule for Pricing PN where these. Bolt = (A - PB)/2 two the pricing rules Producer: intersect PB = (A - PN)/2 A/3 A/2 A PN PB = (A - PN)/2 PN = (A - PB)/2 PN = A/2 - (A - PN)/4 = A/4 + PN/4 3 PN/4 = A/4 PN = A/3 PB + PN = 2 A/3 Q = A - (PB+PN) = A/3 Profit of the Bolt Producer = PBQB = A 2/9 Profit of the Nut Producer = PNQN = A 2/9 Industrial Organization: Chapter 4 49

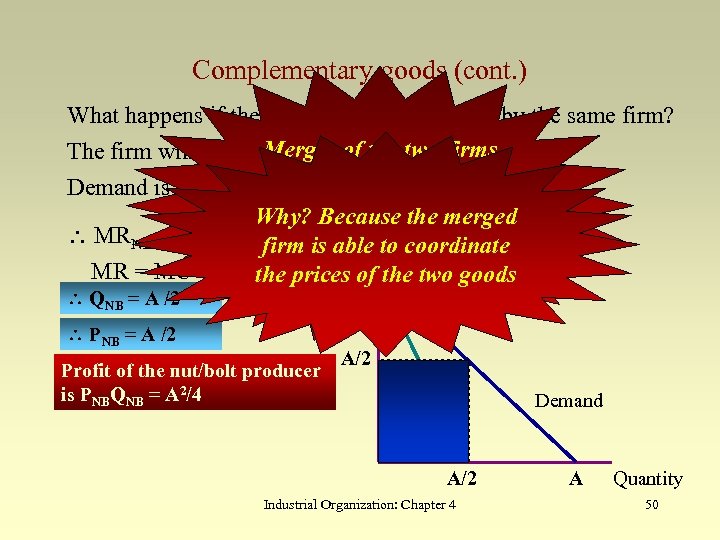Complementary goods (cont. ) What happens if the two goods are produced by the same firm? Merger for a two firms The firm will set a price PNB of thenut/bolt pair. Demand is now QNB =results. NB so that PNB = A - QNB A - P in consumers Why? being charged Because the merged $ MRNB = A - 2 QNB loweris able to coordinate firm prices and the firm making of the profits MR = MC = 0 the pricesgreatertwo goods A QNB = A /2 PNB = A /2 Profit of the nut/bolt producer is PNBQNB = A 2/4 A/2 Demand MR A/2 Industrial Organization: Chapter 4 A Quantity 50

Industrial Organization: Chapter 4 51

Product variety (cont. ) d < 1/4 We know that p(d) satisfies the following constraint: p(d) + t(1/2 - d) = V This gives: p(d) = V - t/2 + t. d Aggregate profit is then: p(d) = (p(d) - c)N = (V - t/2 + t. d - c)N This is increasing in d so if d < 1/4 then d should be increased. Industrial Organization: Chapter 4 52

Product variety (cont. ) d > 1/4 We now know that p(d) satisfies the following constraint: p(d) + t. d = V This gives: p(d) = V - t. d Aggregate profit is then: p(d) = (p(d) - c)N = (V - t. d - c)N This is decreasing in d so if d > 1/4 then d should be decreased. Industrial Organization: Chapter 4 53