Скачать презентацию Chapter 4 Multiple Degree of Freedom Systems The Скачать презентацию Chapter 4 Multiple Degree of Freedom Systems The

1669860efa66520391e0172bfefcc692.ppt

  • Количество слайдов: 58

Chapter 4 Multiple Degree of Freedom Systems The Millennium bridge required many degrees of Chapter 4 Multiple Degree of Freedom Systems The Millennium bridge required many degrees of freedom to model and design with. Extending the first 3 chapters to more then one degree of freedom © D. J. Inman /58 Mechanical Engineering at Virginia Tech

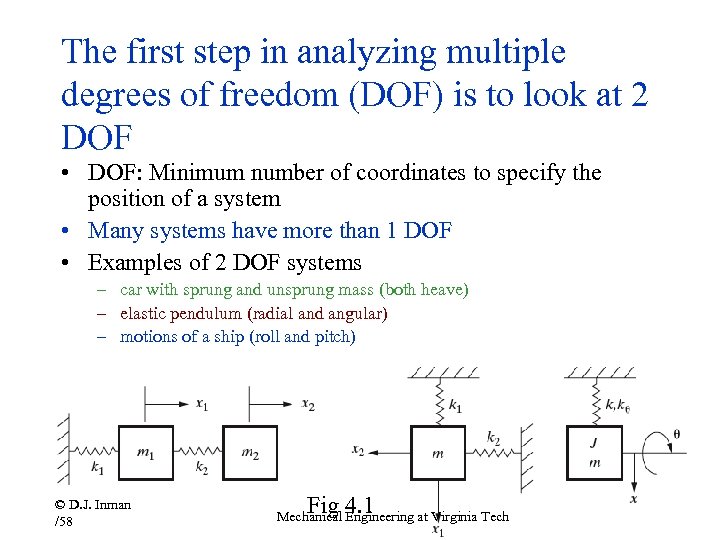The first step in analyzing multiple degrees of freedom (DOF) is to look at The first step in analyzing multiple degrees of freedom (DOF) is to look at 2 DOF • DOF: Minimum number of coordinates to specify the position of a system • Many systems have more than 1 DOF • Examples of 2 DOF systems – car with sprung and unsprung mass (both heave) – elastic pendulum (radial and angular) – motions of a ship (roll and pitch) © D. J. Inman /58 Fig 4. 1 Mechanical Engineering at Virginia Tech

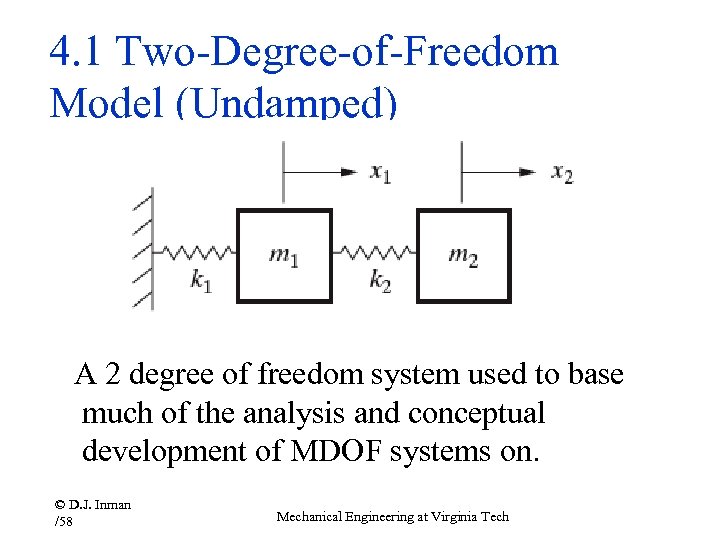4. 1 Two-Degree-of-Freedom Model (Undamped) A 2 degree of freedom system used to base 4. 1 Two-Degree-of-Freedom Model (Undamped) A 2 degree of freedom system used to base much of the analysis and conceptual development of MDOF systems on. © D. J. Inman /58 Mechanical Engineering at Virginia Tech

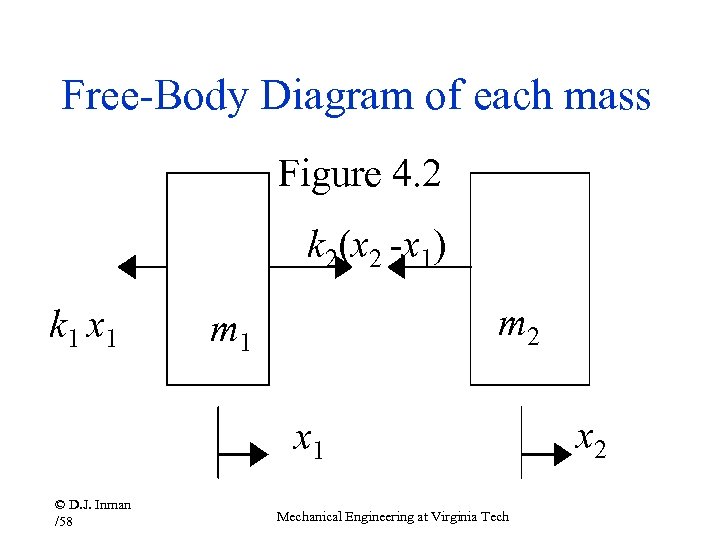Free-Body Diagram of each mass Figure 4. 2 k 2(x 2 -x 1) k Free-Body Diagram of each mass Figure 4. 2 k 2(x 2 -x 1) k 1 x 1 m 2 m 1 x 1 © D. J. Inman /58 Mechanical Engineering at Virginia Tech x 2

Summing forces yields the equations of motion: © D. J. Inman /58 Mechanical Engineering Summing forces yields the equations of motion: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Note that it is always the case that • A 2 Degree-of-Freedom system has Note that it is always the case that • A 2 Degree-of-Freedom system has – Two equations of motion! – Two natural frequencies (as we shall see)! © D. J. Inman /58 Mechanical Engineering at Virginia Tech

The dynamics of a 2 DOF system consists of 2 homogeneous and coupled equations The dynamics of a 2 DOF system consists of 2 homogeneous and coupled equations • Free vibrations, so homogeneous eqs. • Equations are coupled: – Both have x 1 and x 2. – If only one mass moves, the other follows – Example: pitch and heave of a car model • In this case the coupling is due to k 2. – Mathematically and Physically – If k 2 = 0, no coupling occurs and can be solved as two independent SDOF systems © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Initial Conditions • Two coupled, second -order, ordinary differential equations with constant coefficients • Initial Conditions • Two coupled, second -order, ordinary differential equations with constant coefficients • Needs 4 constants of integration to solve • Thus 4 initial conditions on positions and velocities © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Solution by Matrix Methods The two equations can be written in the form of Solution by Matrix Methods The two equations can be written in the form of a single matrix equation (see pages 272 -275 if matrices and vectors are a struggle for you) : (4. 4), (4. 5) (4. 6), (4. 9) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Initial Conditions IC’s can also be written in vector form © D. J. Inman Initial Conditions IC’s can also be written in vector form © D. J. Inman /58 Mechanical Engineering at Virginia Tech

The approach to a Solution: For 1 DOF we assumed the scalar solution aelt The approach to a Solution: For 1 DOF we assumed the scalar solution aelt Similarly, now we assume the vector form: (4. 15) (4. 16) (4. 17) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

This changes the differential equation of motion into algebraic vector equation: © D. J. This changes the differential equation of motion into algebraic vector equation: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

The condition for solution of this matrix equation requires that the matrix inverse does The condition for solution of this matrix equation requires that the matrix inverse does not exist: The determinant results in 1 equation in one unknown (called the characteristic equation) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Back to our specific system: the characteristic equation is defined as (4. 20) (4. Back to our specific system: the characteristic equation is defined as (4. 20) (4. 21) Eq. (4. 21) is quadratic in 2 so four solutions result: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Once is known, use equation (4. 17) again to calculate the corresponding vectors u Once is known, use equation (4. 17) again to calculate the corresponding vectors u 1 and u 2 This yields vector equation for each squared frequency: Each of these matrix equations represents 2 equations in the 2 unknowns components of the vector, but the coefficient matrix is singular so each matrix equation results in only 1 independent equation. The following examples clarify this. © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Examples 4. 1. 5 & 4. 1. 6: calculating u and • m 1=9 Examples 4. 1. 5 & 4. 1. 6: calculating u and • m 1=9 kg, m 2=1 kg, k 1=24 N/m and k 2=3 N/m • The characteristic equation becomes 4 -6 2+8=( 2 -2)( 2 -4)=0 2 = 2 and 2 =4 or Each value of 2 yields an expression or u: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Computing the vectors u 2 equations, 2 unknowns but DEPENDENT! (the 2 nd equation Computing the vectors u 2 equations, 2 unknowns but DEPENDENT! (the 2 nd equation is -3 times the first) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Only the direction of vectors u can be determined, not the magnitude as it Only the direction of vectors u can be determined, not the magnitude as it remains arbitrary © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Likewise for the second value of © D. J. Inman /58 Note that the Likewise for the second value of © D. J. Inman /58 Note that the other equation is the same Mechanical Engineering at Virginia Tech 2:

What to do about the magnitude! Several possibilities, here we just fix one element: What to do about the magnitude! Several possibilities, here we just fix one element: Choose: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Thus the solution to the algebraic matrix equation is: Here we have introduce the Thus the solution to the algebraic matrix equation is: Here we have introduce the name mode shape to describe the vectors u 1 and u 2. The origin of this name comes later © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Return now to the time response: We have computed four solutions: (4. 24) Since Return now to the time response: We have computed four solutions: (4. 24) Since linear, we can combine as: (4. 26) determined by initial conditions. © D. J. Inman /58 Note that to go from the exponential form to to sine requires Euler’s formula for trig functions and uses up the +/- sign on omega Mechanical Engineering at Virginia Tech

Physical interpretation of all that math! • Each of the TWO masses is oscillating Physical interpretation of all that math! • Each of the TWO masses is oscillating at TWO natural frequencies 1 and 2 • The relative magnitude of each sine term, and hence of the magnitude of oscillation of m 1 and m 2 is determined by the value of A 1 u 1 and A 2 u 2 • The vectors u 1 and u 2 are called mode shapes because the describe the relative magnitude of oscillation between the two masses © D. J. Inman /58 Mechanical Engineering at Virginia Tech

What is a mode shape? • First note that A 1, A 2, f What is a mode shape? • First note that A 1, A 2, f 1 and f 2 are determined by the initial conditions • Choose them so that A 2 = f 1 = f 2 =0 • Then: • Thus each mass oscillates at (one) frequency 1 with magnitudes proportional to u 1 the 1 st mode shape © D. J. Inman /58 Mechanical Engineering at Virginia Tech

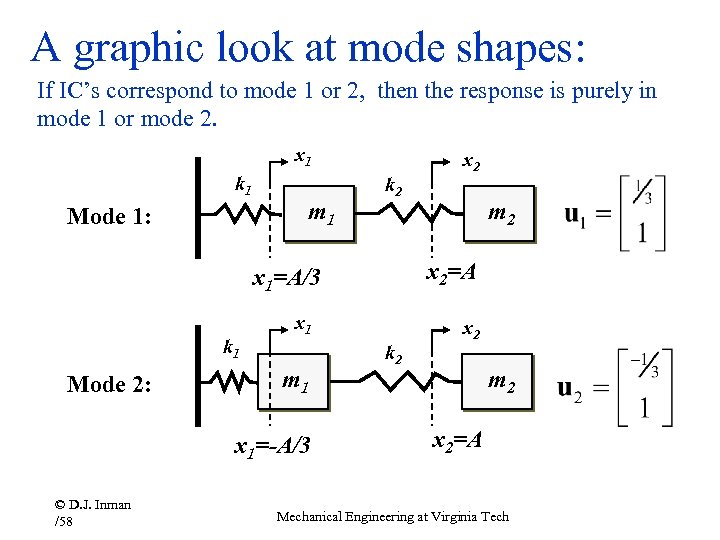A graphic look at mode shapes: If IC’s correspond to mode 1 or 2, A graphic look at mode shapes: If IC’s correspond to mode 1 or 2, then the response is purely in mode 1 or mode 2. x 1 k 1 m 1 Mode 1: k 2 Mode 2: x 1 m 1 x 1=-A/3 © D. J. Inman /58 m 2 x 2=A x 1=A/3 k 1 x 2 k 2 x 2 m 2 x 2=A Mechanical Engineering at Virginia Tech

Example 4. 1. 7 given the initial conditions compute the time response © D. Example 4. 1. 7 given the initial conditions compute the time response © D. J. Inman /58 Mechanical Engineering at Virginia Tech

At t=0 we have © D. J. Inman /58 Mechanical Engineering at Virginia Tech 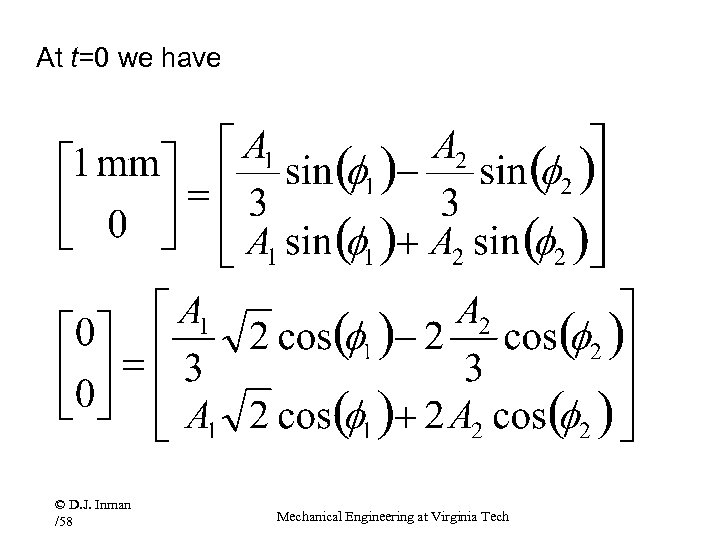At t=0 we have © D. J. Inman /58 Mechanical Engineering at Virginia Tech

4 equations in 4 unknowns: Yields: © D. J. Inman /58 Mechanical Engineering at 4 equations in 4 unknowns: Yields: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

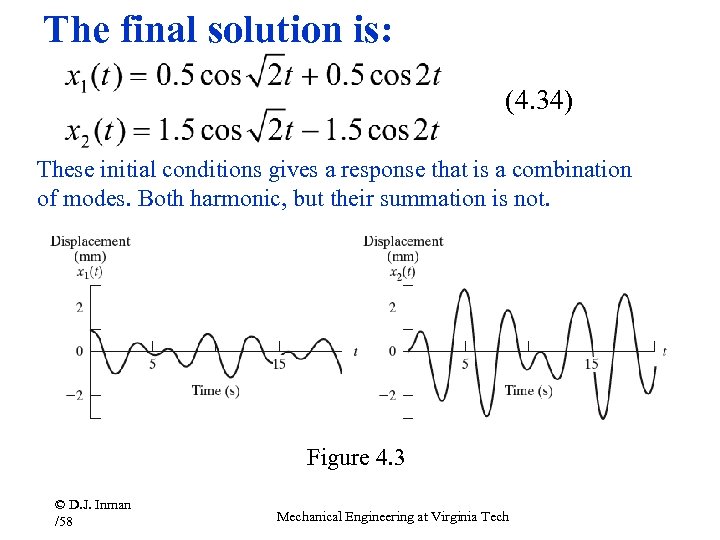The final solution is: (4. 34) These initial conditions gives a response that is The final solution is: (4. 34) These initial conditions gives a response that is a combination of modes. Both harmonic, but their summation is not. Figure 4. 3 © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Solution as a sum of modes Determines how the first frequency contributes to the Solution as a sum of modes Determines how the first frequency contributes to the response © D. J. Inman /58 Determines how the second frequency contributes to the response Mechanical Engineering at Virginia Tech

Things to note • Two degrees of freedom implies two natural frequencies • Each Things to note • Two degrees of freedom implies two natural frequencies • Each mass oscillates at with these two frequencies present in the response and beats could result • Frequencies are not those of two component systems • The above is not the most efficient way to calculate frequencies as the following describes © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Some matrix and vector reminders Then M is said to be positive definite © Some matrix and vector reminders Then M is said to be positive definite © D. J. Inman /58 Mechanical Engineering at Virginia Tech

4. 2 Eigenvalues and Natural Frequencies • Can connect the vibration problem with the 4. 2 Eigenvalues and Natural Frequencies • Can connect the vibration problem with the algebraic eigenvalue problem developed in math • This will give us some powerful computational skills • And some powerful theory • All the codes have eigen-solvers so these painful calculations can be automated © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Some matrix results to help us use available computational tools: A matrix M is Some matrix results to help us use available computational tools: A matrix M is defined to be symmetric if A symmetric matrix M is positive definite if A symmetric positive definite matrix M can be factored Here L is upper triangular, called a Cholesky matrix © D. J. Inman /58 Mechanical Engineering at Virginia Tech

If the matrix L is diagonal, it defines the matrix square root © D. If the matrix L is diagonal, it defines the matrix square root © D. J. Inman /58 Mechanical Engineering at Virginia Tech

A change of coordinates is introduced to capitalize on existing mathematics For a symmetric, A change of coordinates is introduced to capitalize on existing mathematics For a symmetric, positive definite matrix M: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

How the vibration problem relates to the real symmetric eigenvalue problem © D. J. How the vibration problem relates to the real symmetric eigenvalue problem © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Important Properties of the n x n Real Symmetric Eigenvalue Problem • There are Important Properties of the n x n Real Symmetric Eigenvalue Problem • There are n eigenvalues and they are all real valued • There are n eigenvectors and they are all real valued • The set of eigenvectors are orthogonal • The set of eigenvectors are linearly independent • The matrix is similar to a diagonal matrix Window 4. 1 page 285 © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Square Matrix Review • Let aik be the ikth element of A then A Square Matrix Review • Let aik be the ikth element of A then A is symmetric if aik = aki denoted AT=A • A is positive definite if x. TAx > 0 for all nonzero x (also implies each li > 0) • The stiffness matrix is usually symmetric and positive semi definite (could have a zero eigenvalue) • The mass matrix is positive definite and symmetric (and so far, its diagonal) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Normal and orthogonal vectors (4. 43) © D. J. Inman /58 Mechanical Engineering at Normal and orthogonal vectors (4. 43) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Normalizing any vector can be done by dividing it by its norm: (4. 44) Normalizing any vector can be done by dividing it by its norm: (4. 44) To see this compute © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Examples 4. 2. 2 through 4. 2. 4 © D. J. Inman /58 Mechanical Examples 4. 2. 2 through 4. 2. 4 © D. J. Inman /58 Mechanical Engineering at Virginia Tech

The first normalized eigenvector © D. J. Inman /58 Mechanical Engineering at Virginia Tech The first normalized eigenvector © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Likewise the second normalized eigenvector is computed and shown to be orthogonal to the Likewise the second normalized eigenvector is computed and shown to be orthogonal to the first, so that the set is orthonormal © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Modes u and Eigenvectors v are different but related: (4. 37) © D. J. Modes u and Eigenvectors v are different but related: (4. 37) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

This orthonormal set of vectors is used to form an Orthogonal Matrix called a This orthonormal set of vectors is used to form an Orthogonal Matrix called a matrix of eigenvectors (normalized) P is called an orthogonal matrix (4. 47) P is also called a modal matrix © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Example 4. 2. 3 compute P and show that it is an orthogonal matrix Example 4. 2. 3 compute P and show that it is an orthogonal matrix From the previous example: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Example 4. 2. 4 Compute the square of the frequencies by matrix manipulation In Example 4. 2. 4 Compute the square of the frequencies by matrix manipulation In general: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Example 4. 2. 5 The equations of motion: Figure 4. 4 In matrix form Example 4. 2. 5 The equations of motion: Figure 4. 4 In matrix form these become: © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Next substitute numerical values and compute P and © D. J. Inman /58 Mechanical Next substitute numerical values and compute P and © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Next compute the eigenvectors © D. J. Inman /58 Mechanical Engineering at Virginia Tech Next compute the eigenvectors © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Next check the value of P to see if it behaves as its suppose Next check the value of P to see if it behaves as its suppose to: Yes! © D. J. Inman /58 Mechanical Engineering at Virginia Tech

A note on eigenvectors Does this make any difference? No! Try it in the A note on eigenvectors Does this make any difference? No! Try it in the previous example © D. J. Inman /58 Mechanical Engineering at Virginia Tech

All of the previous examples can and should be solved by “hand” to learn All of the previous examples can and should be solved by “hand” to learn the methods However, they can also be solved on calculators with matrix functions and with the codes listed in the last section In fact, for more then two DOF one must use a code to solve for the natural frequencies and mode shapes. Next we examine 3 other formulations for solving for modal data © D. J. Inman /58 Mechanical Engineering at Virginia Tech

Matlab commands • To compute the inverse of the square matrix A: inv(A) or Matlab commands • To compute the inverse of the square matrix A: inv(A) or use Aeye(n) where n is the size of the matrix • [P, D]=eig(A) computes the eigenvalues and normalized eigenvectors (watch the order). Stores them in the eigenvector matrix P and the diagonal matrix D (D= ) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

More commands • • • To compute the matrix square root use sqrtm(A) To More commands • • • To compute the matrix square root use sqrtm(A) To compute the Cholesky factor: L= chol(M) To compute the norm: norm(x) To compute the determinant det(A) To enter a matrix: K=[27 -3; -3 3]; M=[9 0; 0 1]; • To multiply: K*inv(chol(M)) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

An alternate approach to normalizing mode shapes From equation (4. 17) (4. 53) © An alternate approach to normalizing mode shapes From equation (4. 17) (4. 53) © D. J. Inman /58 Mechanical Engineering at Virginia Tech

There are 3 approaches to computing mode shapes and frequencies (i) Is the Generalized There are 3 approaches to computing mode shapes and frequencies (i) Is the Generalized Symmetric Eigenvalue Problem (ii) easy for hand computations, inefficient for computers 1. (ii) Is the Asymmetric Eigenvalue Problem 2. very expensive computationally 3. (iii) Is the Symmetric Eigenvalue Problem 4. the cheapest computationally © D. J. Inman /58 Mechanical Engineering at Virginia Tech