5ad3af7fd462d95bd930daba89a2ab5f.ppt
- Количество слайдов: 66

Chapter 4 Methods of Inference 知識推論法 4. 知識推論法 S. S. Tseng & G. J. Hwang

4. 1 Deductive and Induction (演繹與歸納) • Deduction(演繹): Logical reasoning in which conclusions must follow from their premises. • Induction(歸納): Inference from the specific case to the general. • Intuition(直觀): No proven theory. • Heuristics(啟發): Rules of thumb (觀測法) based upon experience. • Generate and test: Trial and error. 4. 知識推論法 S. S. Tseng & G. J. Hwang 2

• Abduction(反推): Reasoning back from a true conclusion to the premises that may have caused the conclusion. • Autoepitemic(自覺、本能): Self-knowledge • Nonmonotonic(應變知識): previous knowledge may be incorrect when new evidence is obtained • Analogy(類推): based on the similarities to another situation 4. 知識推論法 S. S. Tseng & G. J. Hwang 3

Syllogism (三段論) • Syllogism(三段論)is simple, well-understood branch of logic that can be completely proven. – Premise(前提): Anyone who can program is intelligent – Premise(前提): John can program – Conclusion(結論): Therefore, John is intelligent. • In general, a syllogism is any valid deductive argument having two premises and a conclusion. 4. 知識推論法 S. S. Tseng & G. J. Hwang 4

Categorical Syllogism (定言三段論) 定言命題的型態 形態 概要 意思 A E I O 所有S為P 沒有S為P 某些S不為P 完全肯定 完全否定 部分肯定 部分否定 4. 知識推論法 S. S. Tseng & G. J. Hwang 5

• 三段論的標準形態(Standard form) 大前提:所有M為P 小前提:所有S為M 結論:所有S為P - P代表結論的「謂詞」(Predicate),又稱為「大詞」(Major term) - S代表結論的「主詞」(Subject),又稱作「小詞」(Minor term)。 - 含有大詞的前提稱為「大前提」(Major premise); - 含有小詞的前提稱為「小前提」(Minor premise)。 - M稱為「中詞」(Middle term) 4. 知識推論法 S. S. Tseng & G. J. Hwang 6
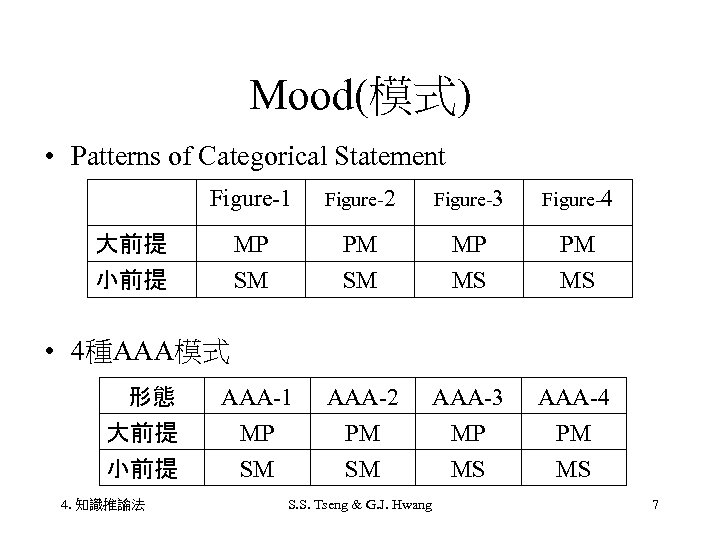
Mood(模式) • Patterns of Categorical Statement Figure-1 Figure-2 Figure-3 Figure-4 MP SM PM SM MP MS PM MS AAA-1 MP SM AAA-2 PM SM AAA-3 MP MS AAA-4 PM MS 大前提 小前提 • 4種AAA模式 形態 大前提 小前提 4. 知識推論法 S. S. Tseng & G. J. Hwang 7

• ex: AAA-1 – 所有M為P 所有S為M ∴所有S為P • We use decision procedure(決策程序) to prove the validity of syllogistic argument • The decision procedure for syllogisms can be done using Venn Diagrams(維思圖) 4. 知識推論法 S. S. Tseng & G. J. Hwang 8

• ex: Decision procedure for Syllogism AEE-1 所有M為P 沒有S為M ∴沒有S為P 4. 知識推論法 S. S. Tseng & G. J. Hwang 9

General Rule under “some” quantifiers 1. If a class is empty, it is shaded. 2. Universal statement, A and E, are always drawn before particular ones. 3. If a class has at least one member, mark it with a *. 4. If a statement does not specify in which of two adjacent classed an object exists, place a * on the line between the classes. 5. If an area has been shaded, no * can be put in it. 4. 知識推論法 S. S. Tseng & G. J. Hwang 10

ex: Decision procedure for Syllogism IAI-1 某些P為M 所有M為S ∴某些S為P 4. 知識推論法 S. S. Tseng & G. J. Hwang 11

4. 2 State and problem spaces (狀態與問題空間) • Tree(樹狀結構): nodes, edges • Directed or undirected • Digraph(雙向圖): a graph with directed edges • Lattice(晶格): a directed acyclic graph 4. 知識推論法 S. S. Tseng & G. J. Hwang 12

• A useful method of describing the behavior of an object is to define a graph called the state space. [state(狀態) and action(行動)] – – – Initial state Operator State space Path Goal test Path cost 4. 知識推論法 S. S. Tseng & G. J. Hwang 13
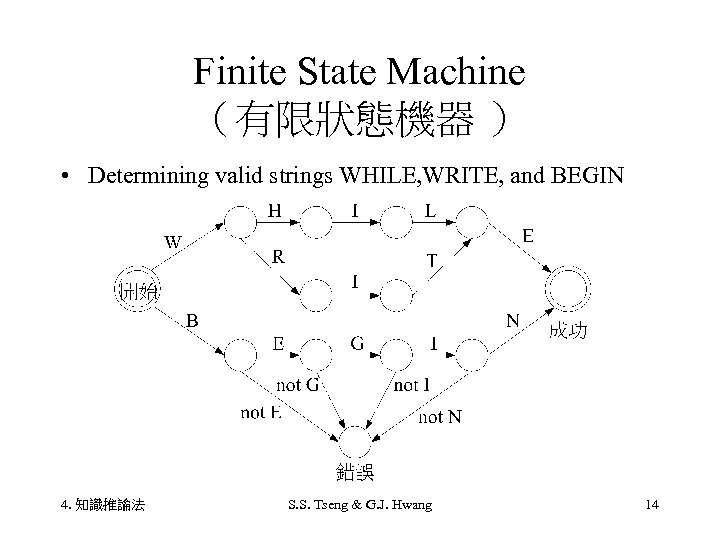
Finite State Machine (有限狀態機器 ) • Determining valid strings WHILE, WRITE, and BEGIN 4. 知識推論法 S. S. Tseng & G. J. Hwang 14

Finding solution in problem space • State space(狀態空間) can be thought as a problem space(問題空間). • Finding the solution to a problem in a problem space involves finding a valid path from start to success( answer). • The state space for the Monkey and Bananas Problem • Traveling salesman problem(旅行推銷員問題) • Graph algorithms, AND-OR Trees, etc. 4. 知識推論法 S. S. Tseng & G. J. Hwang 15
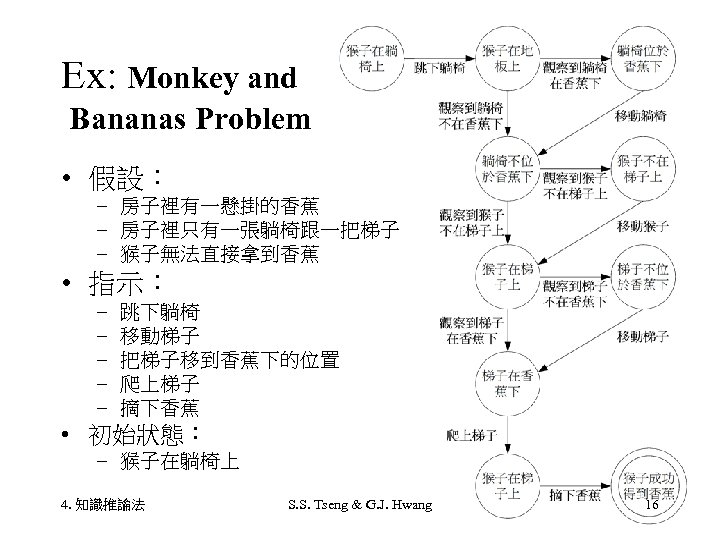
Ex: Monkey and Bananas Problem • 假設: – 房子裡有一懸掛的香蕉 – 房子裡只有一張躺椅跟一把梯子 – 猴子無法直接拿到香蕉 • 指示: – – – 跳下躺椅 移動梯子 把梯子移到香蕉下的位置 爬上梯子 摘下香蕉 • 初始狀態: – 猴子在躺椅上 4. 知識推論法 S. S. Tseng & G. J. Hwang 16
Ex: Travel Salesman Problem (旅行推銷員問題) 4. 知識推論法 S. S. Tseng & G. J. Hwang 17

Ill-structured problem (非結構化問題) • Ill-structured problems(非結構化問題) have uncertainties associated with it. – Goal not explicit – Problem space unbounded – Problem space not discrete – Intermediate states difficult to achieve – State operators unknown – Time constraint 4. 知識推論法 S. S. Tseng & G. J. Hwang 18

Ex: 旅遊代理人 特徵 客戶的反應 目標不明顯 我在想到底要去哪裡 問題空間範圍未被介 定 我不確定要去哪裡 問題狀態不是離散的 我只是想去旅遊,目的地並 不重要 我沒有足夠的錢去 中間的狀態不易實行 狀態的可用運算元未 知 時間限制 4. 知識推論法 我不知道怎麼可以籌到錢 我必須儘快出發 S. S. Tseng & G. J. Hwang 19

4. 3 Rules of Inference(規則式推論) • Syllogism(三段論) addresses only a small portion of the possible logic statements. • Propositional logic p q p______ q Inference is called direct reasoning (直接推論), modus ponens (離斷率), law of detachment (分離 律) , and assuming the antecedent (假設前提). 4. 知識推論法 S. S. Tseng & G. J. Hwang 20

Truth table for Modus Ponense(離斷率) p q p→q (p→q) p (p→q) p→q T T T T F T F T F T F F T F T 4. 知識推論法 S. S. Tseng & G. J. Hwang 21

Law of Inference Schemata p→q 1. Law of Detachment p ∴q 2. Law of the Contrapositive p→q ∴~q→~p 3. Law of Modus Tollens p→q ~q ∴~p 4. Chain Rules(Law of the Syllogism) P→q q→r ∴p→r 5. Law of Disjunctive Inference p q ~p ∴q ~(~p) ∴p 6. Law of the Double Negation 4. 知識推論法 S. S. Tseng & G. J. Hwang p q ~q ∴p 22

7. De Morgan’s Law ~(p q) ∴~p ~q ~(p q) ∴~p ~q 8. Law of Simplification p q ∴p ~(p q) ∴~q 9. Law of Conjunction p q ∴p q 10. Law of Disjunctive Addition p ∴p q 11. Law of Conjunctive Argument ~(p q) p ∴~q ~(p q) q ∴~p Table 3. 8 Some Rules of Inference for Propositional Logic 4. 知識推論法 S. S. Tseng & G. J. Hwang 23

Resolution in propositional Logic (命題邏輯分解) 命題邏輯 F: Rules or facts known to be TRUE S: A conclusion to be Proved • Convert all the propositions of F to clause form. 2. Negate S and convert the result to clause form. Add it to the set of clauses obtained in step 1. 3. Repeat until either a contradiction is found or no progress can be made: (1) Select two clauses. Call these the Parent clauses. 4. 知識推論法 S. S. Tseng & G. J. Hwang 24

(2) Resolve them together. The resulting clause, called the resolvent, will be the disjunction of all of the literals of both of the parent clauses with the following exception:If there any pairs of literals L and ~L. Such that one of the parent clauses contains L and the other contaions ~L, then eliminate both L and ~L from the resolvent. (3) If the resolvent is the empty clause, then a contradiction has been found. If it is not, then add it to the set of clauses available to the procedure. 4. 知識推論法 S. S. Tseng & G. J. Hwang 25

Given Axioms Converted to Clause Form p p (p q) r 1. ~p ~q r (s t) q ~s q ~t q t t 2. 3. 4. 5. p =下雨 q = 騎車 s = 路線熟悉 t = 路途遠 r = 穿雨衣 4. 知識推論法 S. S. Tseng & G. J. Hwang 26
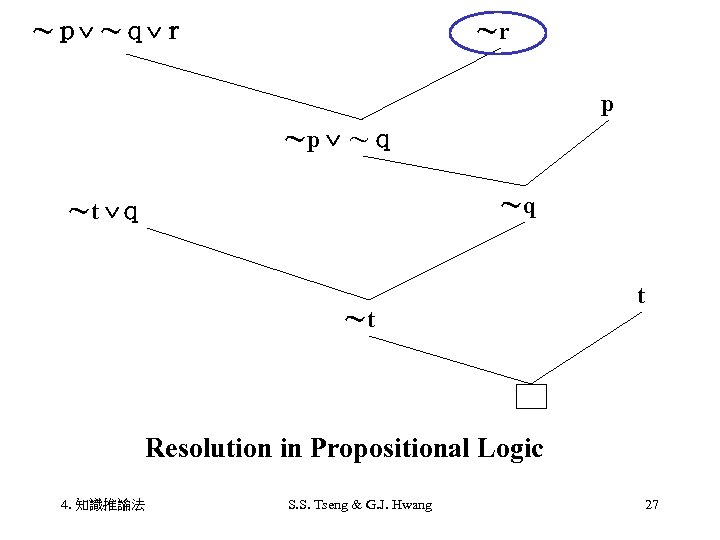
~p ~q r ~r p ~p ~q ~q ~t q ~t t Resolution in Propositional Logic 4. 知識推論法 S. S. Tseng & G. J. Hwang 27

Resolution with quantifiers Example(from Nilsson): Whoever can read (R) is literate (L). Dolphins (D) aren’t literate (~L). Some dolphins (D) are intelligent (I). To prove:Some who are intelligent (I) can’t read (~R). 4. 知識推論法 S. S. Tseng & G. J. Hwang 28
![Translating: x[R(x)→ L(x)] x [ D ( x ) → ~L ( x ) Translating: x[R(x)→ L(x)] x [ D ( x ) → ~L ( x )](https://present5.com/presentation/5ad3af7fd462d95bd930daba89a2ab5f/image-29.jpg)
Translating: x[R(x)→ L(x)] x [ D ( x ) → ~L ( x ) ] x[D(x) & I(x)] To prove: x [ I ( x ) & ~ R ( x ) ] 4. 知識推論法 S. S. Tseng & G. J. Hwang 29

(1) - (4): x [~ R ( x ) OR L ( x ) ] & y [ ~ D ( y ) OR ~ L ( y ) ] & D ( A ) & I ( A ) & z [~ I ( z ) OR R ( z ) ] (5) - (9): C 1=~R(x) OR L(x) C 2=~D(y) OR ~L(y) C 3=D(A) C 4=I(A) C 5= ~I(z) OR R(z) 4. 知識推論法 S. S. Tseng & G. J. Hwang 30

• The second order logic can have quantifiers that range over function and predicate symbols • If P is any predicate of one document – Then – x =y (for every P [P(x) P(y) ] 4. 知識推論法 S. S. Tseng & G. J. Hwang 31
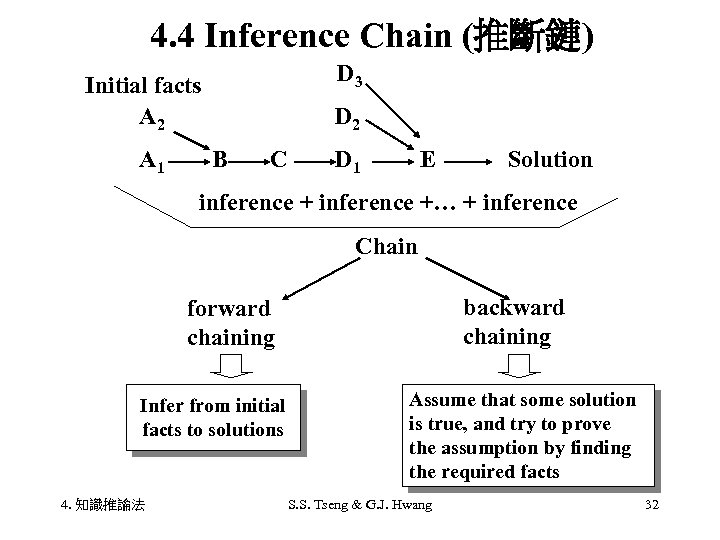
4. 4 Inference Chain (推斷鏈) Initial D 3 facts A 2 D 2 A 1 B C D 1 E Solution inference +… + inference Chain backward chaining forward chaining Infer from initial facts to solutions 4. 知識推論法 Assume that some solution is true, and try to prove the assumption by finding the required facts S. S. Tseng & G. J. Hwang 32
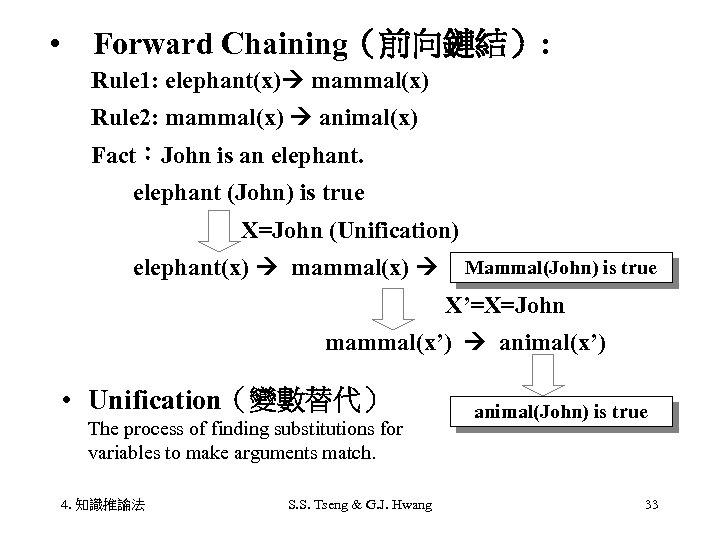
• Forward Chaining(前向鏈結): Rule 1: elephant(x) mammal(x) Rule 2: mammal(x) animal(x) Fact:John is an elephant. elephant (John) is true X=John (Unification) elephant(x) mammal(x) X’=X=John mammal(x’) animal(x’) • Unification(變數替代) The process of finding substitutions for variables to make arguments match. 4. 知識推論法 Mammal(John) is true S. S. Tseng & G. J. Hwang animal(John) is true 33
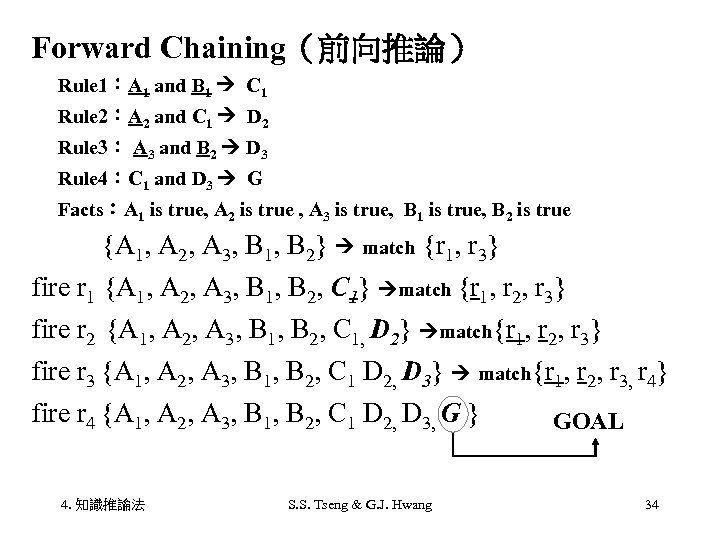
Forward Chaining(前向推論) Rule 1:A 1 and B 1 C 1 Rule 2:A 2 and C 1 D 2 Rule 3: A 3 and B 2 D 3 Rule 4:C 1 and D 3 G Facts:A 1 is true, A 2 is true , A 3 is true, B 1 is true, B 2 is true {A 1, A 2, A 3, B 1, B 2} match {r 1, r 3} fire r 1 {A 1, A 2, A 3, B 1, B 2, C 1} match {r 1, r 2, r 3} fire r 2 {A 1, A 2, A 3, B 1, B 2, C 1, D 2} match{r 1, r 2, r 3} fire r 3 {A 1, A 2, A 3, B 1, B 2, C 1 D 2, D 3} match{r 1, r 2, r 3, r 4} fire r 4 {A 1, A 2, A 3, B 1, B 2, C 1 D 2, D 3, G } GOAL 4. 知識推論法 S. S. Tseng & G. J. Hwang 34
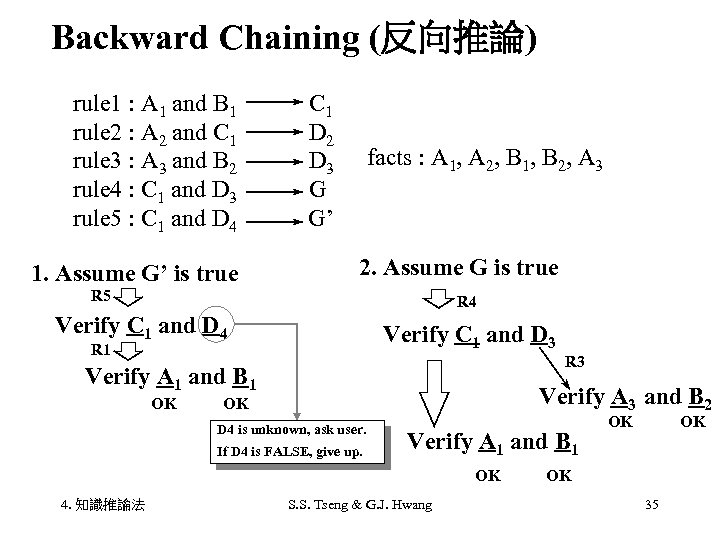
Backward Chaining (反向推論) rule 1 : A 1 and B 1 rule 2 : A 2 and C 1 rule 3 : A 3 and B 2 rule 4 : C 1 and D 3 rule 5 : C 1 and D 4 1. Assume G’ is true C 1 D 2 D 3 G G’ facts : A 1, A 2, B 1, B 2, A 3 2. Assume G is true R 5 R 4 Verify C 1 and D 3 R 1 R 3 Verify A 1 and B 1 OK Verify A 3 and B 2 OK D 4 is unknown, ask user. If D 4 is FALSE, give up. Verify A 1 and B 1 OK 4. 知識推論法 S. S. Tseng & G. J. Hwang OK OK OK 35
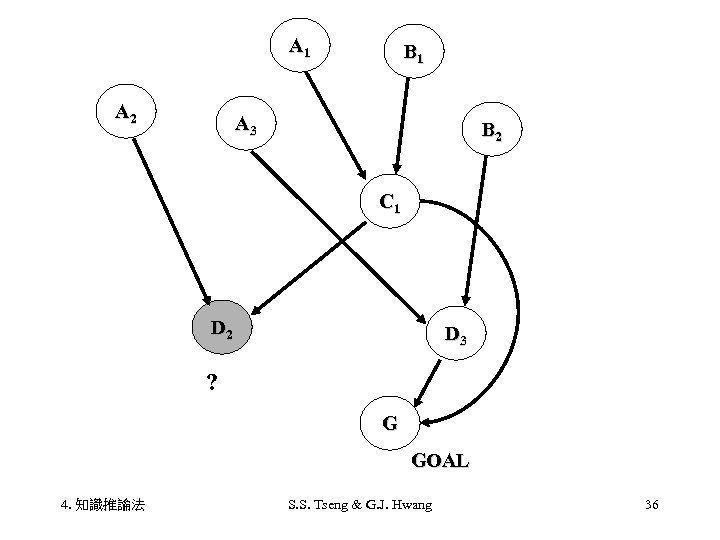
A 1 A 2 B 1 A 3 B 2 C 1 D 2 D 3 ? G GOAL 4. 知識推論法 S. S. Tseng & G. J. Hwang 36
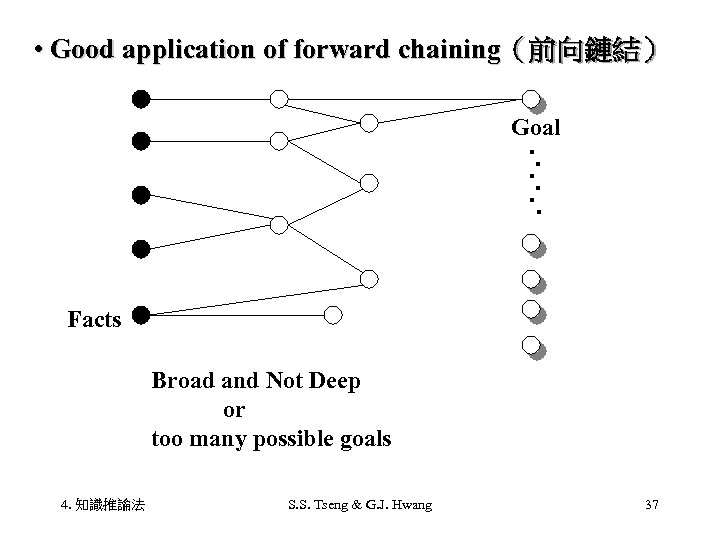
• Good application of forward chaining(前向鏈結) Goal Facts Broad and Not Deep or too many possible goals 4. 知識推論法 S. S. Tseng & G. J. Hwang 37
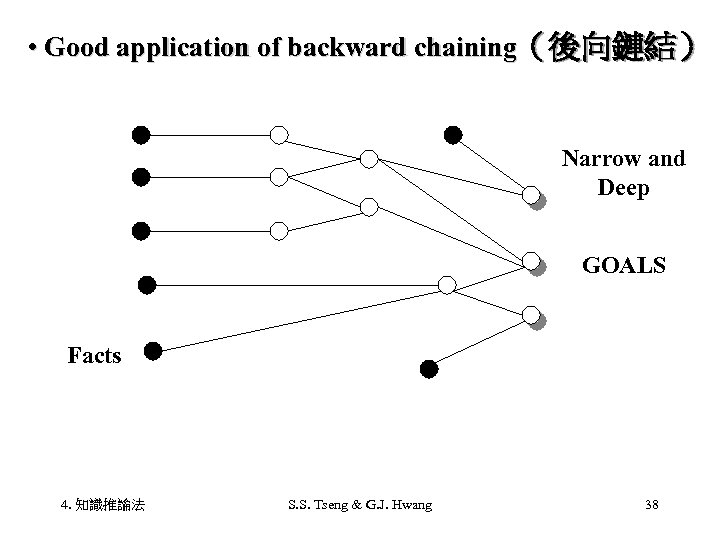
• Good application of backward chaining(後向鏈結) Narrow and Deep GOALS Facts 4. 知識推論法 S. S. Tseng & G. J. Hwang 38

• Forward Chaining(前向鏈結) Planning Monitoring Control Data-driven Explanation not facilitated • Backward chaining(後向鏈結) Diagnosis Goal-driven Explanation facilitated 4. 知識推論法 S. S. Tseng & G. J. Hwang 39

Analogy • Try to relate old situations as guides to new ones • Consider tic-tac-toe with values as a magic square (15 game) » 6 » 7 » 2 1 5 9 8 3 4 • 18 game from set {2, 3, 4, 5, 6, 7, 8, 9, 10} • 21 game from set {3, 4, 5, 6, 7, 8, 9, 10, 11} 4. 知識推論法 S. S. Tseng & G. J. Hwang 40

Nonmonotonic reasoning • In nonmonotonic system, theorems do not necessarily increase as the number of axioms increases. • As a very simple example, suppose there is a fact that asserts the time. As soon as time changes by a second, the old fact is no longer valid. 4. 知識推論法 S. S. Tseng & G. J. Hwang 41

4. 5 Reasoning Under Uncertainty (不確定性推論) • Uncertainty can be considered as the lack of adequate information to make a decision. • Classical probability, Bayescian probability, Dempster. Shafer theory, and Zadeh’s fuzzy theory. • In the MYCIN and PROSPECTOR systems conclusion are arrived at even when all the evidence needed to absolutely prove the conclusion is not known. 4. 知識推論法 S. S. Tseng & G. J. Hwang 42

Many different types of error can contribute to uncertainty Example Turn the value off Turn value-1 off Value is stuck Value is not stuck Turn value-1 to 5. 4 or 6 or 0 Value-1 setting is 5. 4 or 5. 5 or 5. 1 Value-1 setting is 7. 5 Value-1 is not stuck because it’s never been stuck before Output is normal and so value-1 is in good condition 4. 知識推論法 Error Ambiguous Incomplete Incorrect False positive (接受錯誤值) False negative (拒絕正確值) Imprecise Inaccurate Unreliable Random error Systematic error Invalid induction Reason What value? Which way? Correct is on Value is not stuck Value is stuck Correct is 5. 4 Correct is 9. 2 Equipment error Statistical fluctuation (波動) Mis-calibration (刻度) Invalid deduction Value is stuck in open position S. S. Tseng & G. J. Hwang Value is stuck 43

• A hypothesis is an assumption to be tested. • Type 1 error (false positive) means acceptance of a hypothesis when it is not true. • Type 2 error (false negative) means rejection of a hypothesis when it is true. • Error of measurement – Precision • The millimeter(公釐) ruler is more precise than centimeter ruler. – accuracy 4. 知識推論法 S. S. Tseng & G. J. Hwang 44

Error & Induction The process of induction is the opposite of deduction The fire alarm goes off (響起) ∴ There is a fire. An even stronger argument is The fire alarm goes off & I smell smoke ∴ There is a fire. Although this is a strong argument, it is not proof that there is a fire. My clothes are burning 4. 知識推論法 S. S. Tseng & G. J. Hwang 45

Deductive errors p→q q ∴ p If John is a father, than John is a man ∴ John is a father 4. 知識推論法 S. S. Tseng & G. J. Hwang 46

Baye’s Theorem (貝氏定理) • Conditional probability(條件機率), P(A | B) , states the probability of event B occurred. Crash= Brand X(0. 6)+ Not X(0. 1)=0. 7 • P( X|C) = P( C | X) P(X) = P(C) (0. 75)(0. 8) = 0. 7 6 7 • Suppose you have a drive and don’t know its brand, what is the probability that if it crashes, it is Brand X? non. Brand X? 4. 知識推論法 S. S. Tseng & G. J. Hwang 47
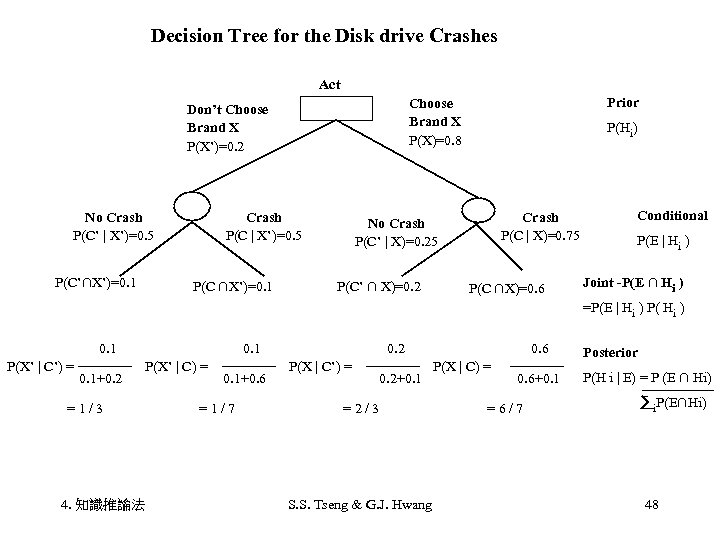
Decision Tree for the Disk drive Crashes Act No Crash P(C’ | X’)=0. 5 P(C’∩X’)=0. 1 Crash P(C | X’)=0. 5 P(C ∩X’)=0. 1 Prior Choose Brand X P(X)=0. 8 Don’t Choose Brand X P(X’)=0. 2 P(Hi) Crash P(C | X)=0. 75 No Crash P(C’ | X)=0. 25 P(C’ ∩ X)=0. 2 P(C ∩X)=0. 6 Conditional P(E | Hi ) Joint -P(E ∩ Hi ) =P(E | Hi ) P( Hi ) 0. 1 P(X’ | C’) = 0. 1+0. 2 =1/3 4. 知識推論法 0. 1 P(X’ | C) = 0. 1+0. 6 =1/7 0. 2 P(X | C’) = 0. 2+0. 1 =2/3 S. S. Tseng & G. J. Hwang 0. 6 P(X | C) = 0. 6+0. 1 =6/7 Posterior P(H i | E) = P (E ∩ Hi) i. P(E∩Hi) 48

P(E∩Hi) P(E | H i) P(Hi | E) = = P(E ∩Hj) P(E | Hj) P(Hj) j j P(E | Hi)P(Hi) = P(E) • Bayes’ Theorem(貝氏定理) is commonly used for decision tree analysis of business and the social science. • Used in Prospector expert system to decide favorite sites of mineral exploration 4. 知識推論法 S. S. Tseng & G. J. Hwang 49
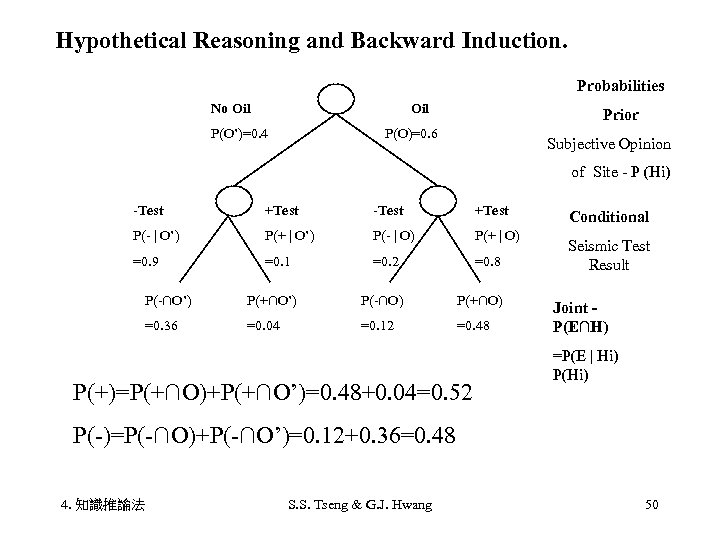
Hypothetical Reasoning and Backward Induction. Probabilities No Oil P(O’)=0. 4 Prior P(O)=0. 6 Subjective Opinion of Site - P (Hi) -Test +Test P(- | O’) P(+ | O’) P(- | O) P(+ | O) =0. 9 =0. 1 =0. 2 =0. 8 P(-∩O’) P(+∩O’) P(-∩O) P(+∩O) =0. 36 =0. 04 =0. 12 =0. 48 P(+)=P(+∩O)+P(+∩O’)=0. 48+0. 04=0. 52 Conditional Seismic Test Result Joint P(E∩H) =P(E | Hi) P(-)=P(-∩O)+P(-∩O’)=0. 12+0. 36=0. 48 4. 知識推論法 S. S. Tseng & G. J. Hwang 50
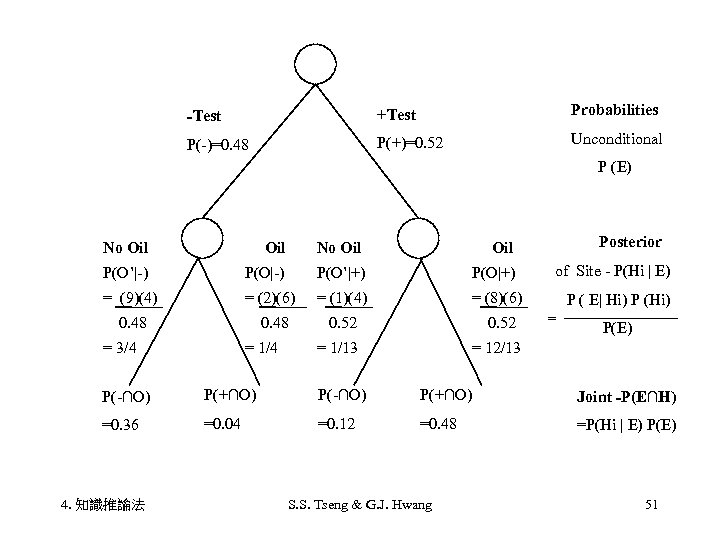
-Test +Test Probabilities P(-)=0. 48 P(+)=0. 52 Unconditional P (E) No Oil P(O’|-) P(O’|+) P(O|+) = (9)(4) = (2)(6) = (1)(4) Posterior Oil = (8)(6) 0. 48 = 3/4 = 1/4 0. 52 = 1/13 of Site - P(Hi | E) P ( E| Hi) P (Hi) = P(E) = 12/13 P(-∩O) P(+∩O) Joint -P(E∩H) =0. 36 =0. 04 =0. 12 =0. 48 =P(Hi | E) P(E) 4. 知識推論法 S. S. Tseng & G. J. Hwang 51

• • Oil release , if successful Drilling expense Seismic survey Expected payoff (success) $1250000 -$200000 -$50000 • 846153=1000000 *12/13 – 1000000*1/13 • Fail • -500000= 1000000*1/4 - 1000000*3/4 • Expected payoff (total) • 416000= 846153*0. 52 – 50000 * 0. 48 4. 知識推論法 S. S. Tseng & G. J. Hwang 52

Temporal reasoning and Markov chain • Temporal reasoning: reasoning about events that depend on time • Temporal logic • The system’s progression through a sequence of status is called a Stochastic process if it is probabilistic. 4. 知識推論法 S. S. Tseng & G. J. Hwang 53

– P 11 P 12 – P 21 P 22 – Where Pmn is the probability of a transition from state m to state n. S = { P 1, P 2, …, Pn} where P 1+P 2+…+Pn= 1 S 2 = S 1 T 0. 1 0. 9 S 2 = [0. 8, 0. 2] = [0. 2, 0. 8] 0. 6 4. 知識推論法 0. 4 S. S. Tseng & G. J. Hwang 54

• Assume 10 percent of all people who now use Brand X drive will buy another Brand X when needed. 60 percent of people who don’t use Brand X will buy Brand X when they need a new drive. Over a period of time, how many people will use Brand X? S 3 = [0. 5, 0. 5], S 4 = [0. 35, 0. 65], S 5 = [0. 425, 0. 575], S 6 = [0. 3875, 0. 6125] S 7 = [0. 40625, 0. 59375], S 8 = [0. 396875, 0. 602125] Steady state matrix 4. 知識推論法 S. S. Tseng & G. J. Hwang 55

The odds of belief • “The patient is covered with red spots” • Proposition A: “The patient has measles” • P(A|B) : (degree of belief that A is true, given B)is not necessarily a probability if the events and propositions can not be repeated or has a math basis. 4. 知識推論法 S. S. Tseng & G. J. Hwang 56

• The odds on A against B given some event C are odds =P(A|C)/ P(B|C) • If B = A’ – odds =P(A|C)/ P(A’|C) =P(A|C)/ (1 -P(A|C) ) • Likelihood of P = 0. 95 – Odds =. 95/(1 -. 95) = 19 to 1 4. 知識推論法 S. S. Tseng & G. J. Hwang 57

Sufficiency and necessity Bayes’ Theorem is P(E | H)P(H) P(H|E) = P(E) Negation P(H’|E) = P(E | H’)P(H’) P(E) 4. 知識推論法 58 S. S. Tseng & G. J. Hwang

P(H | E) = P(E | H) P(H’ | E) P(E | H’) P(H’) Defining the prior odds on H as P(H) O(H) = P(H’) P(H | E) O(H | E) = P(H’ | E) 4. 知識推論法 S. S. Tseng & G. J. Hwang 59

Likelihood ratio P(E | H) LS= P(E | H’) O(H | E) = LS O(H) odds-likelihood form of Bayes’ Theorem. The factor LS is also called likelihood of sufficiency because if LS =∞ then the evidence E is logically sufficient for concluding that H is true. 4. 知識推論法 S. S. Tseng & G. J. Hwang 60

Likelihood of necessity, LN, is defined similarly to LS as P(H | E’) O(H | E’) P(E’ | H) P(H’ | E’) LN= = = O(H) P(E’ | H’) P(H) P(H’) O(H | E’) = LN O(H) LN=0, then P(H | E’) = 0. This means that H must be false when E’ true. Thus if E is not present then H is false, which means that E is necessary for H. 4. 知識推論法 S. S. Tseng & G. J. Hwang 61

LS Effect on Hypothesis 0 H is false when E is true or E’ is necessary for concluding H Small(0<LS<<1) E is unfavorable for concluding H 1 E has no effect on belief of H Large(1<<LS) E is favorable for concluding H E is logically sufficient for H or Observing E means H must be true 4. 知識推論法 S. S. Tseng & G. J. Hwang 62

LN Effect on Hypothesis 0 H is false when E is true or E is necessary for H small(0<LN<<1) Absence of E is unfavorable for concluding H 1 Absence of E has no effect on H large(1<<LN) Absence of E is favorable of H Absence of E is logically sufficient for H 4. 知識推論法 S. S. Tseng & G. J. Hwang 63

Uncertainty in inference chains • Uncertainty may be present in rules, evidence used by the rules, or both. 4. 知識推論法 S. S. Tseng & G. J. Hwang 64

Expert Inconsistency If LS > 1 then P(E | H’) < P(E | H) 1 – P(E | H’) > 1 – P(E | H) 1 -P(E | H) LN= 1 -P(E | H’) <1 Case 1:LS>1 and LN <1 Case 2:LS<1 and LN >1 Case 3:LS= LN = 1 4. 知識推論法 S. S. Tseng & G. J. Hwang 65

Exercise • 考慮以下的事實與規則,試以前向鏈結和後向鏈結描述其推論過程。 事實: A 1, A 2, A 3, A 4, B 1, B 2 規則: R 1: A 1 and A 3 --> C 2 R 2: A 1 and B 1 --> C 1 R 3: A 2 and C 2 --> D 2 R 4: A 3 and B 2 --> D 3 R 5: C 1 and D 2 --> G 1 R 6: B 1 and B 2 --> D 4 R 7: A 1 and A 2 and A 3 --> D 2 R 8: C 1 and D 3 --> G 2 R 9: C 2 and A 4 --> G 3 目標: G 1, G 2 and G 3 4. 知識推論法 S. S. Tseng & G. J. Hwang 66
5ad3af7fd462d95bd930daba89a2ab5f.ppt