Chapter 4 Decision Making 1 Advanced Organizer

Chapter 4 Decision Making 1

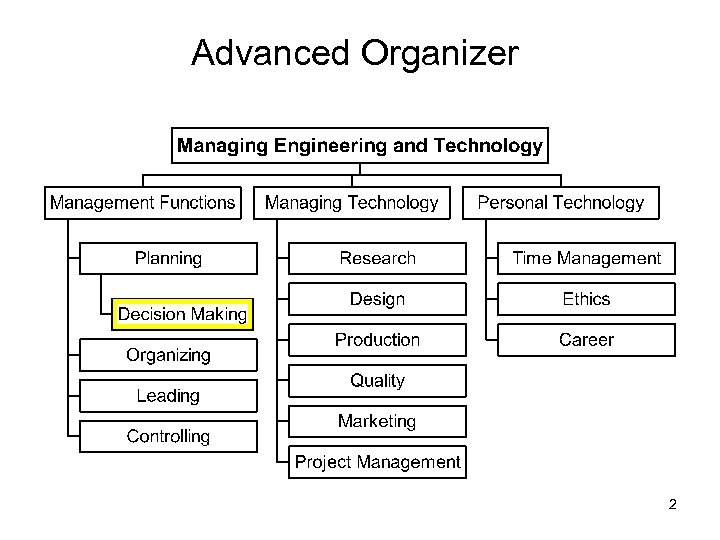Advanced Organizer 2

Chapter Objectives • Discuss how decision making relates to planning • Explain the process of engineering problem solving • Be able to solve problems using three types of decision making tools • Discuss the differences between decision making under certainty, risk, and uncertainty • Describe the basics of other decision making techniques 3

Relation to Planning § Managerial decision making is the process of making a conscious choice between two or more rational alternatives 4

Types of Decisions • Routine and Non-Routine Decisions • Objective vs. Bounded Rationality • Level of Certainty 5

Management Science Characteristics • Systems view of the problem • Team approach • Emphasis on use of formal mathematical models and statistical and quantitative techniques 6

Models & Analysis • • • Formulate the problem Construct a mathematical model Test the model’s ability Derive a solution from the model Apply model’s solution to real system 7

Categories of Decision Making • Decision Making under Certainty (Only one state of nature exists. ) • Decision Making under Risk (Probabilities for states of natures are known. ) • Decision Making under Uncertainty (Probabilities for states of natures are unknown. ) 8

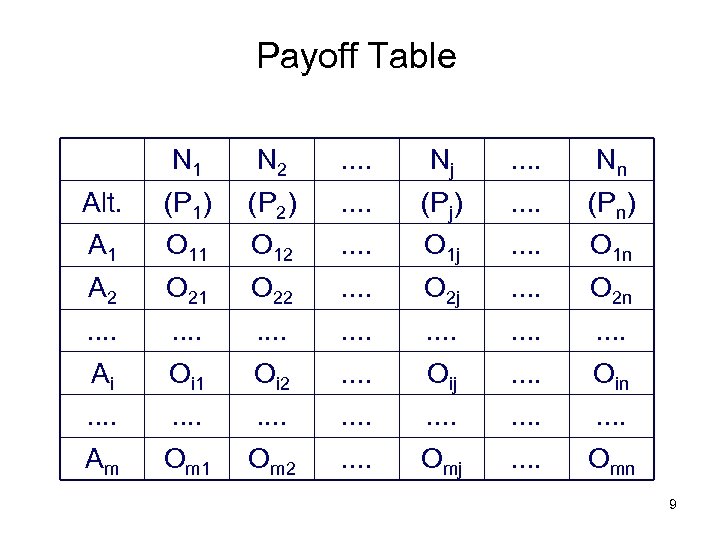Payoff Table N 1 N 2 . . Nj . . Nn Alt. (P 1) (P 2) . . (Pj) . . (Pn) A 1 O 12 . . O 1 j . . O 1 n A 2 O 21 O 22 . . O 2 j . . O 2 n . . . . Ai Oi 1 Oi 2 . . Oij . . Oin . . . . Am Om 1 Om 2 . . Omj . . Omn 9

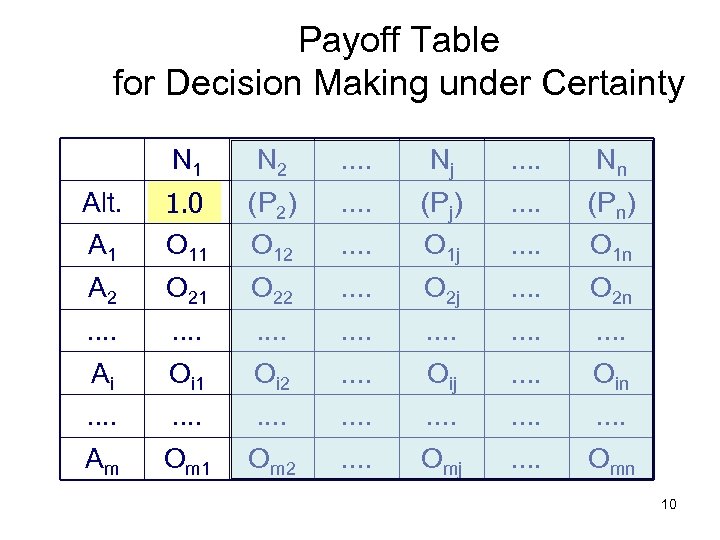Payoff Table for Decision Making under Certainty N 1 N 2 . . Nj . . Nn (P 2) . . (Pj) . . (Pn) A 1 (P 1) 1. 0 O 11 O 12 . . O 1 j . . O 1 n A 2 O 21 O 22 . . O 2 j . . O 2 n . . . . Ai Oi 1 Oi 2 . . Oij . . Oin . . . . Am Om 1 Om 2 . . Omj . . Omn Alt. 10

Tools for Decision Making under Certainty • Linear programming – Graphical solution – Simplex method – Computer software • Non-linear programming • Engineering Economic Analysis 11

Linear Programming • Decision Variables • Objective Function (Maximizing or Minimizing) – Example: • A factory produces two products, product X and product Y. If we can realize $10 profit per unit of product X and $14 per unit of Y, what should be the production level for product X and product Y? – Maximize P = 10 x + 14 y 12

Linear Programming • Constrains – Example: • • 3 machinists 2 assemblers Each works 40 hours/week Product X requires 3 hours of machining and 1 hour of assembly per unit • Product Y requires 2 hours of machining and 2 hours of assembly per unit – For machining time: 3 x + 2 y 3(40) – For assembly time: 1 x + 2 y 2(40) 13

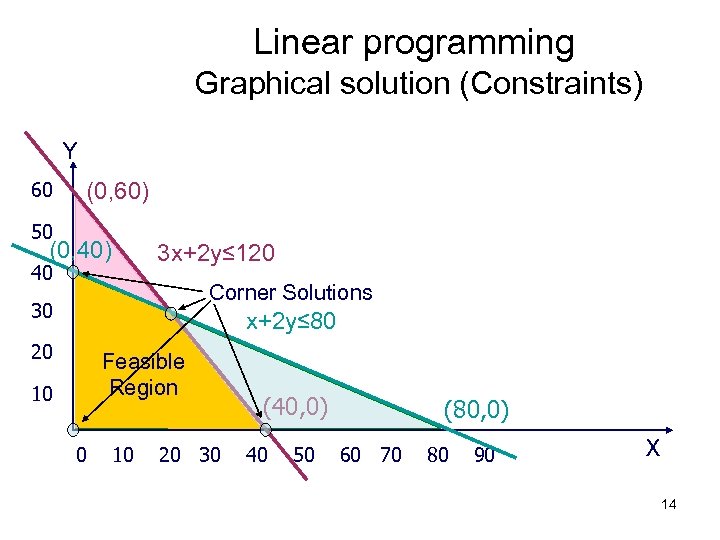Linear programming Graphical solution (Constraints) Y 60 (0, 60) 50 (0, 40) 3 x+2 y≤ 120 40 Corner Solutions 30 x+2 y≤ 80 20 Feasible Region 10 0 10 20 30 (40, 0) 40 50 (80, 0) 60 70 80 90 X 14

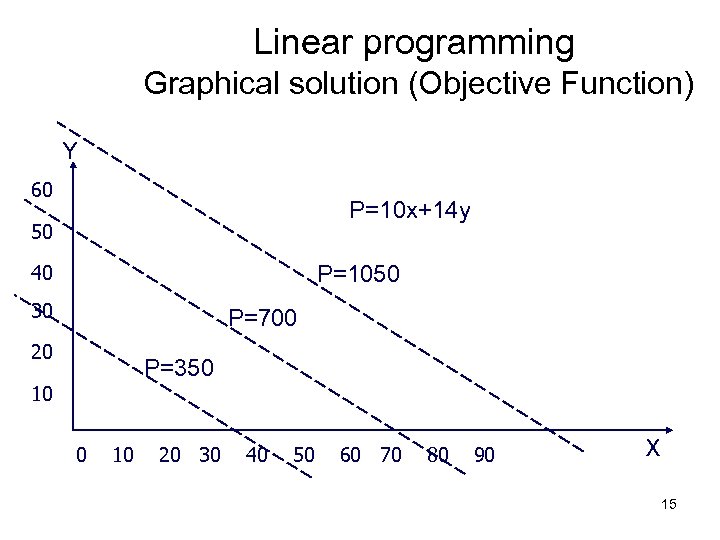Linear programming Graphical solution (Objective Function) Y 60 P=10 x+14 y 50 40 P=1050 30 P=700 20 P=350 10 20 30 40 50 60 70 80 90 X 15

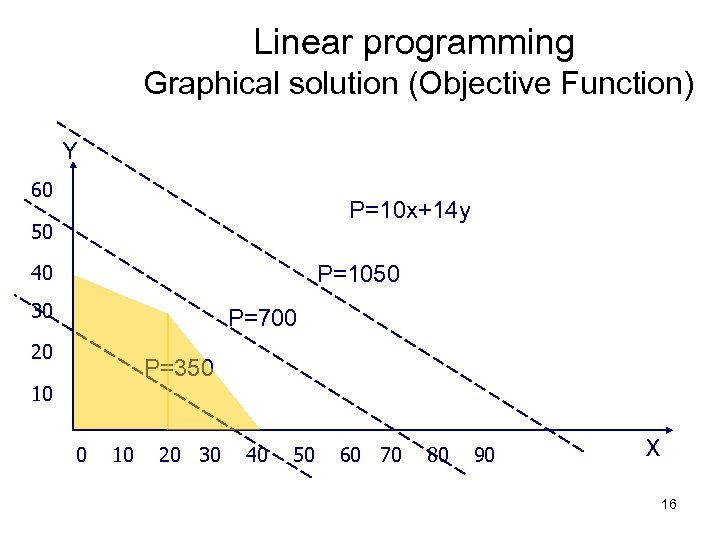Linear programming Graphical solution (Objective Function) Y 60 P=10 x+14 y 50 40 P=1050 30 P=700 20 P=350 10 20 30 40 50 60 70 80 90 X 16

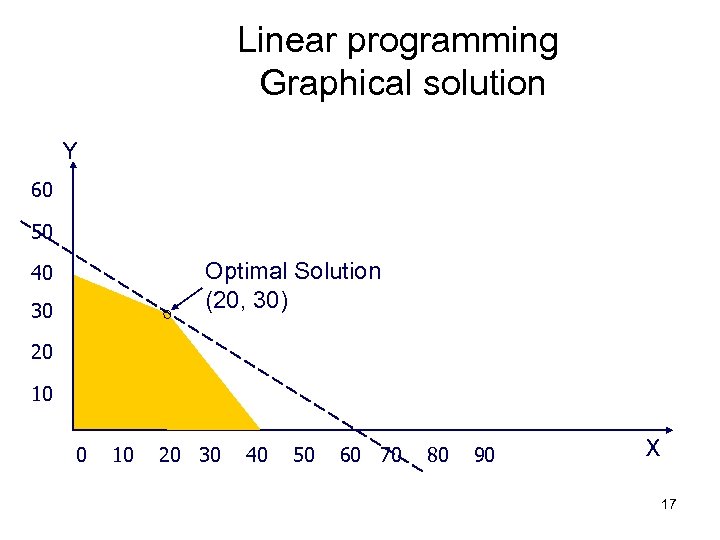Linear programming Graphical solution Y 60 50 Optimal Solution (20, 30) 40 30 20 10 20 30 40 50 60 70 80 90 X 17

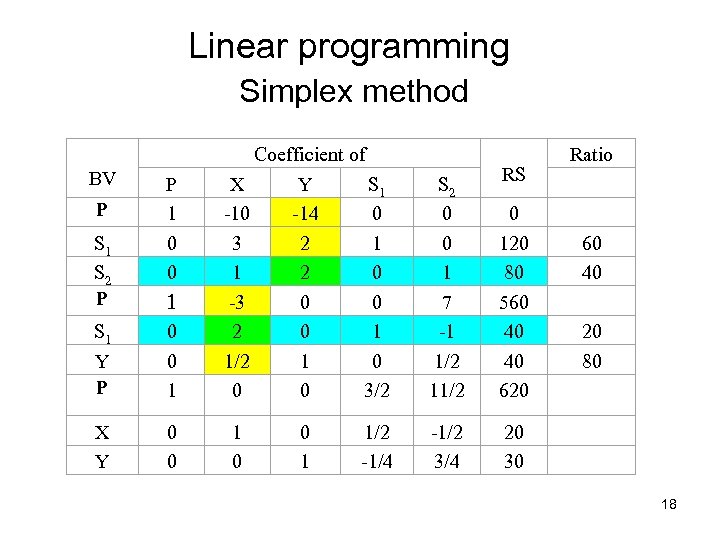Linear programming Simplex method BV P S 1 S 2 P P 1 0 0 S 1 Y P 1 0 0 1 X Y 0 0 Coefficient of X Y S 1 -10 -14 0 3 2 1 1 2 0 -3 0 0 2 0 1 1 0 1/2 0 0 3/2 1 0 0 1 1/2 -1/4 RS S 2 0 0 1 7 -1 1/2 11/2 0 120 80 560 40 40 620 -1/2 3/4 20 30 Ratio 60 40 20 80 18

Linear programming Computer Software • Excel: Solver • LINDO: www. lindo. com max 10 x + 14 y subject to M) 3 x + 2 y <= 120 A) x + 2 y <= 80 end 19

Engineering Economic Analysis • Time Value of Money • Minimum Acceptable Rate of Return • Decision Criteria – Net Present Worth – Equivalent Annual Worth – Internal Rate of Return – Benefit / Cost Ratio 20

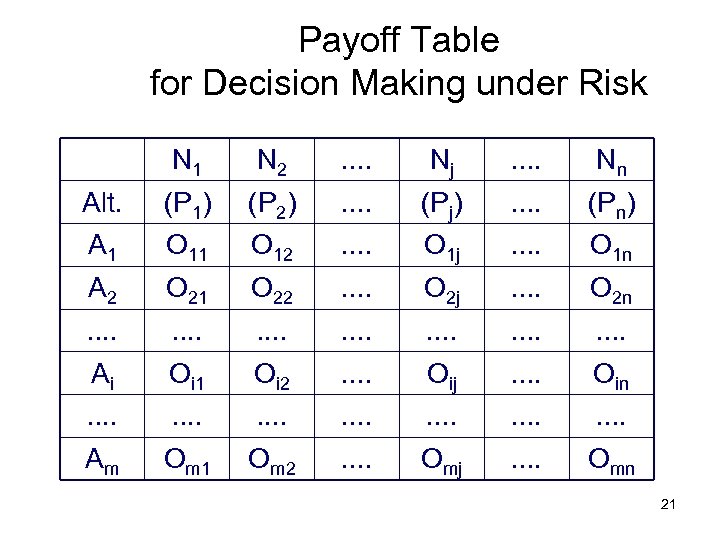Payoff Table for Decision Making under Risk N 1 N 2 . . Nj . . Nn Alt. (P 1) (P 2) . . (Pj) . . (Pn) A 1 O 12 . . O 1 j . . O 1 n A 2 O 21 O 22 . . O 2 j . . O 2 n . . . . Ai Oi 1 Oi 2 . . Oij . . Oin . . . . Am Om 1 Om 2 . . Omj . . Omn 21

Tools for Decision Making under Risk • Expected value • Decision trees Decision Node Chance Node • Queuing theory • Simulation 22

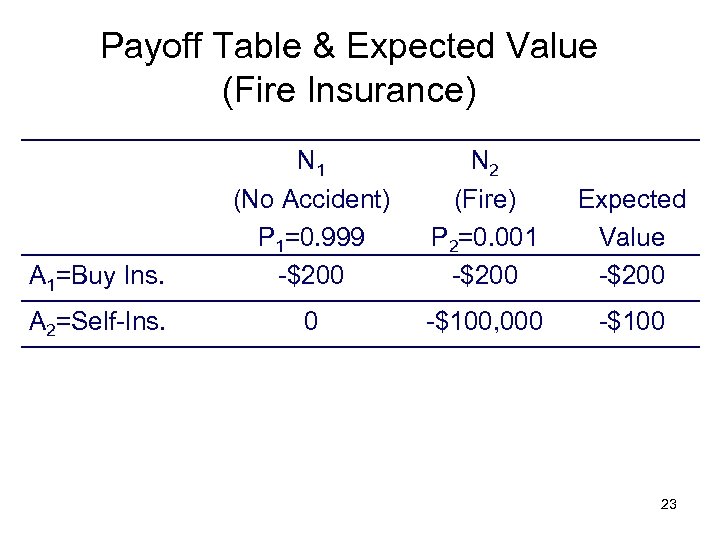Payoff Table & Expected Value (Fire Insurance) A 1=Buy Ins. N 1 (No Accident) P 1=0. 999 -$200 N 2 (Fire) P 2=0. 001 -$200 Expected Value -$200 A 2=Self-Ins. 0 -$100, 000 -$100 23

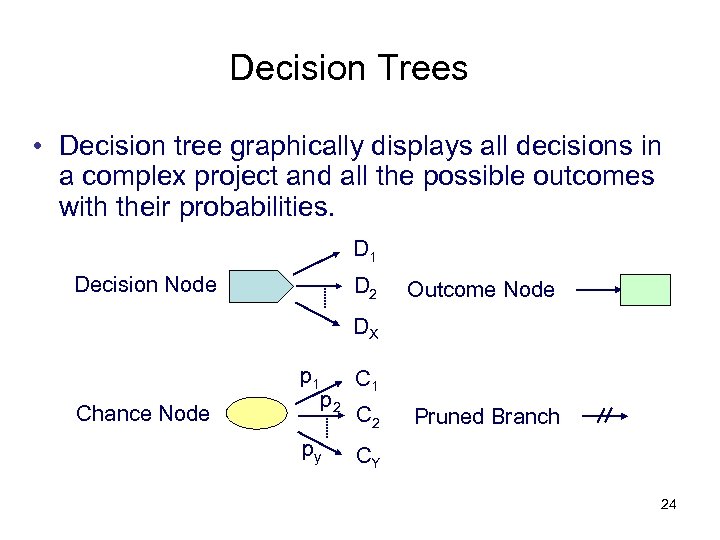Decision Trees • Decision tree graphically displays all decisions in a complex project and all the possible outcomes with their probabilities. D 1 Decision Node D 2 Outcome Node DX p 1 Chance Node p 2 py C 1 C 2 Pruned Branch CY 24

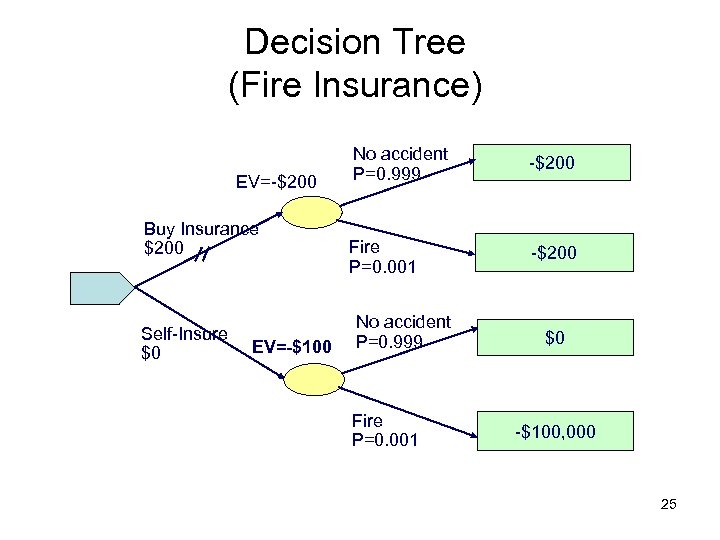Decision Tree (Fire Insurance) EV=-$200 Buy Insurance $200 Self-Insure $0 EV=-$100 No accident P=0. 999 P=0. 9 -$200 Fire P=0. 001 -$200 No accident P=0. 999 Fire P=0. 001 $0 -$100, 000 25

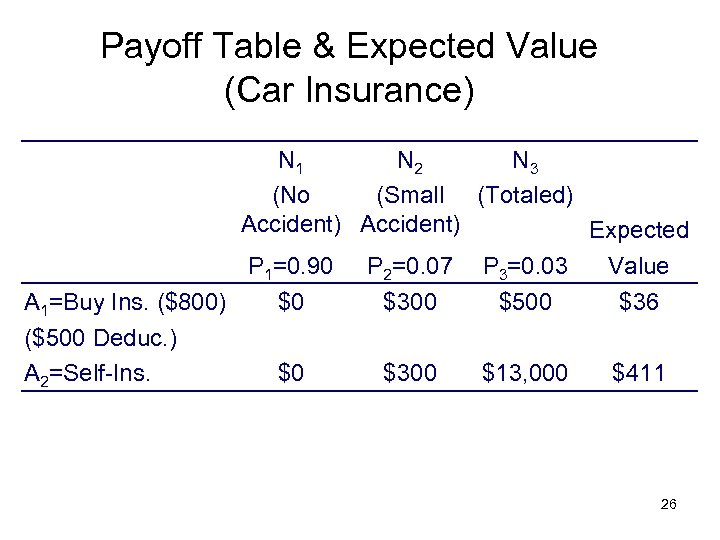Payoff Table & Expected Value (Car Insurance) N 1 N 2 N 3 (No (Small (Totaled) Accident) Expected P 1=0. 90 P 2=0. 07 P 3=0. 03 Value A 1=Buy Ins. ($800) $0 $300 $500 $36 ($500 Deduc. ) A 2=Self-Ins. $0 $300 $13, 000 $411 26

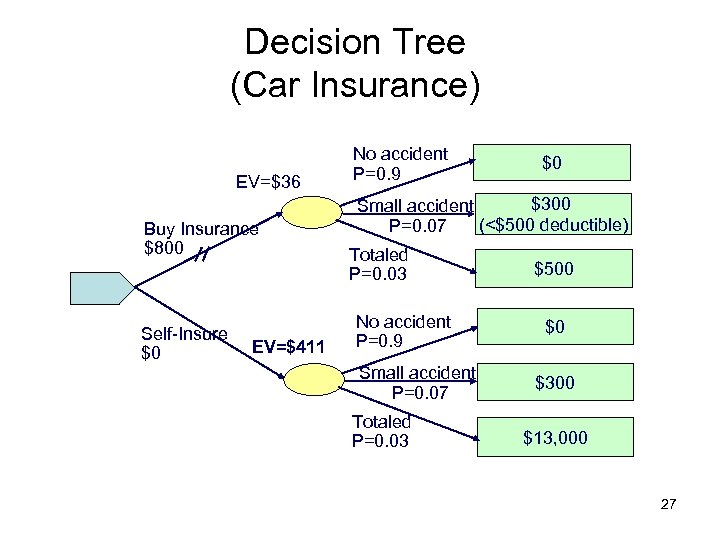Decision Tree (Car Insurance) EV=$36 Buy Insurance $800 Self-Insure $0 EV=$411 No accident P=0. 9 $0 $300 Small accident (<$500 deductible) P=0. 07 Totaled P=0. 03 No accident P=0. 9 Small accident P=0. 07 Totaled P=0. 03 $500 $0 $300 $13, 000 27

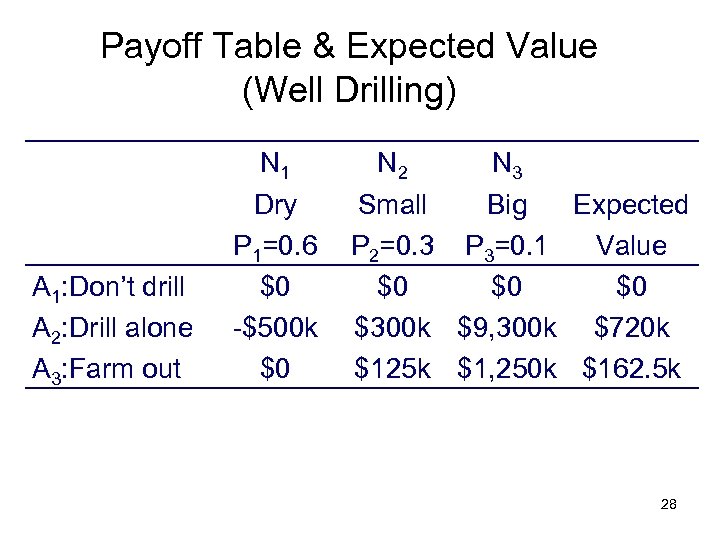Payoff Table & Expected Value (Well Drilling) A 1: Don’t drill A 2: Drill alone A 3: Farm out N 1 Dry P 1=0. 6 $0 -$500 k $0 N 2 N 3 Small Big Expected P 2=0. 3 P 3=0. 1 Value $0 $0 $0 $300 k $9, 300 k $720 k $125 k $1, 250 k $162. 5 k 28

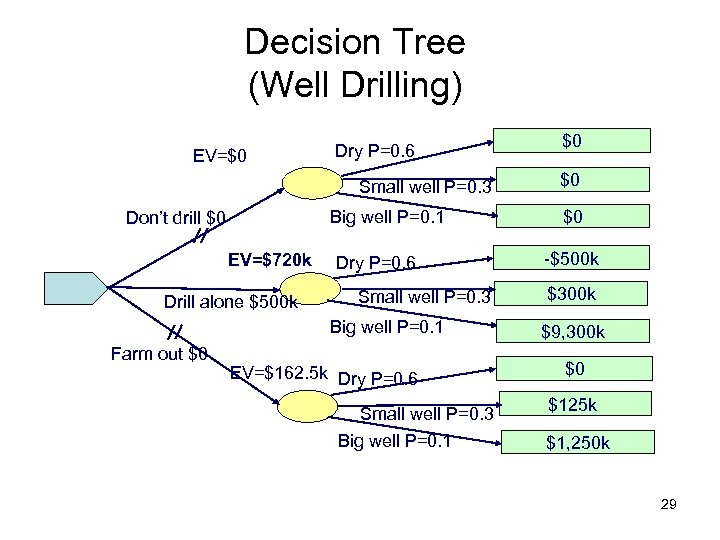Decision Tree (Well Drilling) EV=$0 Dry P=0. 6 Small well P=0. 3 Big well P=0. 1 Don’t drill $0 EV=$720 k Drill alone $500 k Dry P=0. 6 Small well P=0. 3 Big well P=0. 1 Farm out $0 EV=$162. 5 k Dry P=0. 6 Small well P=0. 3 Big well P=0. 1 $0 $0 $0 -$500 k $300 k $9, 300 k $0 $125 k $1, 250 k 29

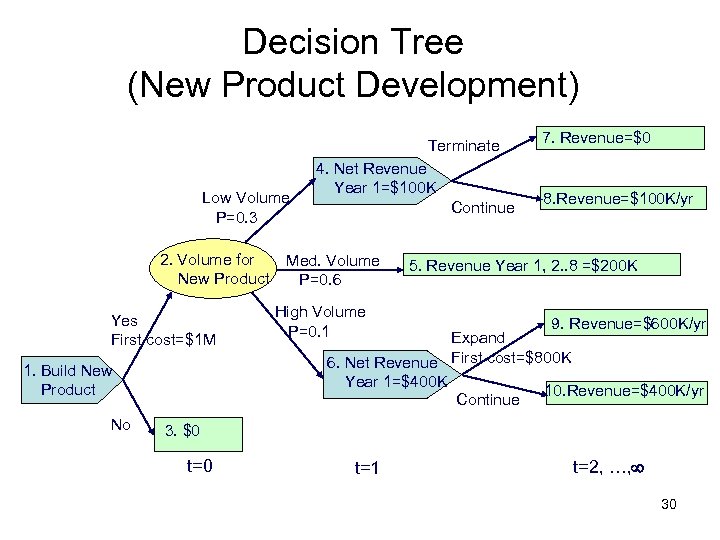Decision Tree (New Product Development) Terminate Low Volume P=0. 3 2. Volume for New Product Yes First cost=$1 M 1. Build New Product No 4. Net Revenue Year 1=$100 K Continue Med. Volume P=0. 6 7. Revenue=$0 8. Revenue=$100 K/yr 5. Revenue Year 1, 2. . 8 =$200 K High Volume P=0. 1 9. Revenue=$600 K/yr Expand 6. Net Revenue First cost=$800 K Year 1=$400 K 10. Revenue=$400 K/yr Continue 3. $0 t=1 t=2, …, 30

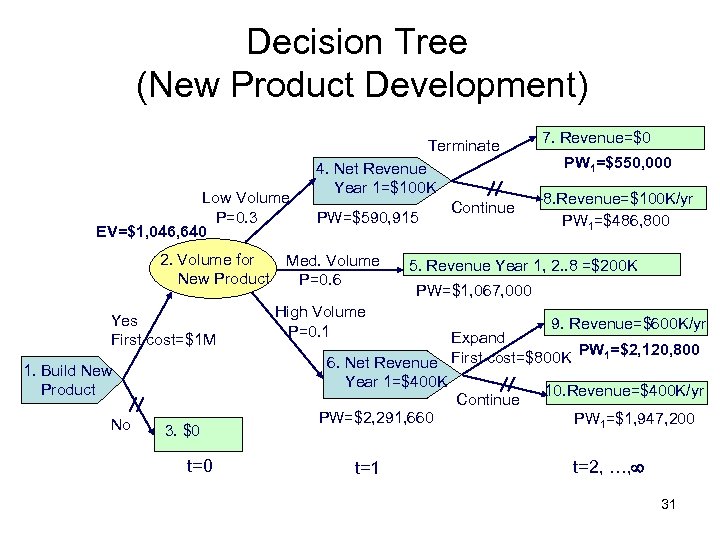Decision Tree (New Product Development) Terminate Low Volume P=0. 3 EV=$1, 046, 640 2. Volume for New Product Yes First cost=$1 M 1. Build New Product No 3. $0 t=0 4. Net Revenue Year 1=$100 K PW=$590, 915 Med. Volume P=0. 6 Continue 7. Revenue=$0 PW 1=$550, 000 8. Revenue=$100 K/yr PW 1=$486, 800 5. Revenue Year 1, 2. . 8 =$200 K PW=$1, 067, 000 High Volume P=0. 1 9. Revenue=$600 K/yr Expand First cost=$800 K PW 1=$2, 120, 800 6. Net Revenue Year 1=$400 K 10. Revenue=$400 K/yr Continue PW=$2, 291, 660 PW 1=$1, 947, 200 t=1 t=2, …, 31

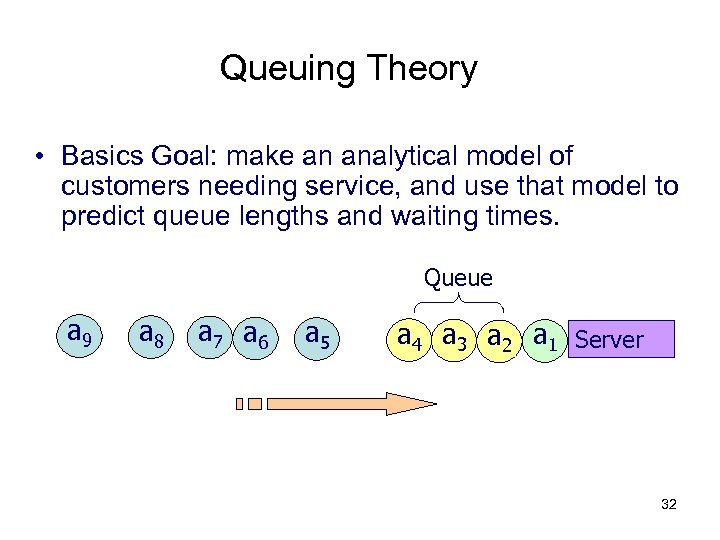Queuing Theory • Basics Goal: make an analytical model of customers needing service, and use that model to predict queue lengths and waiting times. Queue a 9 a 8 a 7 a 6 a 5 a 4 a 3 a 2 a 1 Server 32

Queuing Theory - Terminology • Customers — independent entities that arrive at random times to a Server and wait for service, then leave. • Server — can only service one customer at a time; length of time to provide service depends on type of service; customers are served in FIFO order. • Time — real, continuous, time. • Queue — customers that have arrived at server but are waiting for their service to start are in the queue. • Queue Length at time t — number of customers in the queue at time t. • Waiting Time — for a given customer, how long that customer has to wait between arriving at the server and when the server actually starts the service (total time is waiting time plus service time). 33

Types of Queuing Models • M/M/1 — exponential arrival rate and service times, with 1 server (like office hours). • M/M/m — exponential arrival rate and service times, with m servers (like grocery store with many checkout lanes). • M/M/m/m — exponential arrival rate and service times, with m servers, but nobody waits in queue (if all m servers are busy when a customer arrives, that customer gives up and leaves). • M/M/ — exponential arrival rate and service times, with unlimited number of servers (customers never wait in queue). 34

Types of Queuing Models • M/D/1 —service times are deterministic (e. g. a constant, fixed service time regardless of customer). • M/G/1 — exponential arrival rate, but service rate has a “general” (arbitrary) probability distribution, and a single server. • M/G/m —same as above, but with m servers. 35

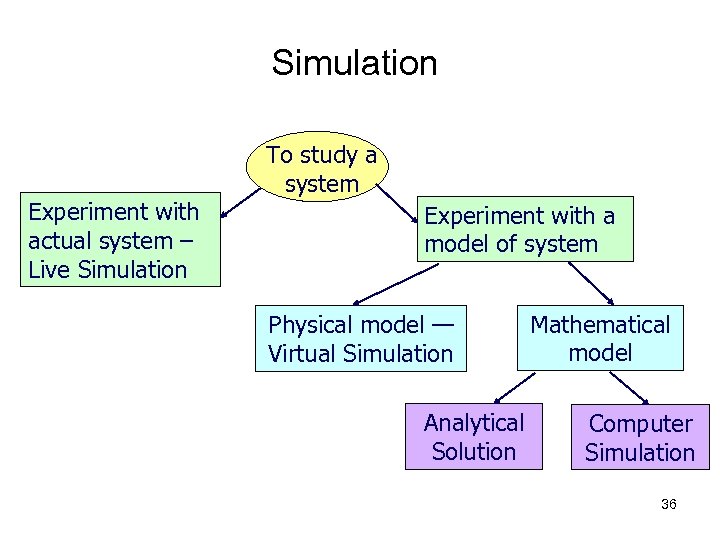Simulation Experiment with actual system – Live Simulation To study a system Experiment with a model of system Physical model — Virtual Simulation Analytical Solution Mathematical model Computer Simulation 36

Simulation modeling seeks to: • Describe the behavior of a system • Use the model to predict future behavior, i. e. the effects that will be produced by changes in the system or in its method of operation. 37

Simulation Types of Simulation Modes: • Continuous Simulation – For systems vary continually with time • Discrete Simulation – For systems change only at discrete set of points in time (state changes) • Hybrid 38

Applications of Simulation • Testing new designs, layouts without committing resources to their implementation • Exploring new policies, procedures, rules, structures, information flows, without disrupting the ongoing operations. • Identifying bottlenecks in information, material and product flows and test options for increasing the flow rates. • Testing hypothesis about how or why certain phenomena occur in the system. • Gaining insights into how a system works and which variables are most important to performance. • Experimenting with new and unfamiliar situations and to answer "what if" questions. 39

Advantages and Limitations of Simulation + Easy to comprehend + Credible because the behavior can be validated + Fewer simplifying assumptions - Requires specialized training and skills Utility of the study depends upon the quality of the model Data Gathering reliable input data can be time consuming “Run" rather than solved. Do not yield an optimal solution, rather they serve as a tool for analysis 40

Simulation Tools • General purpose language – C, C++, Java, Visual BASIC • General simulation language – Discrete simulation: Auto. Mod, Arena, GASP, GPSS, SIMAN, Sim. Py, SIMSCRIPT II. 5 – Continuous simulation: ACSL, Dynamo, SLAM , Vis. Sim – Hybrid: Ecosim. Pro Language (EL), Saber-Simulator, Simulink, Z simulation language, Flexsim 4. 0 • Special purpose simulation package – Chemical process, electrical circuits, transportation 41

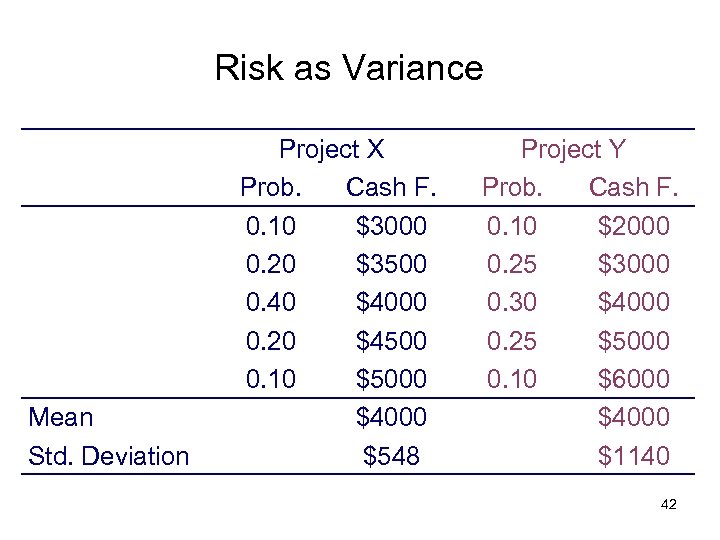Risk as Variance Mean Std. Deviation Project X Prob. Cash F. 0. 10 $3000 0. 20 $3500 0. 40 $4000 0. 20 $4500 0. 10 $5000 $4000 $548 Project Y Prob. Cash F. 0. 10 $2000 0. 25 $3000 0. 30 $4000 0. 25 $5000 0. 10 $6000 $4000 $1140 42

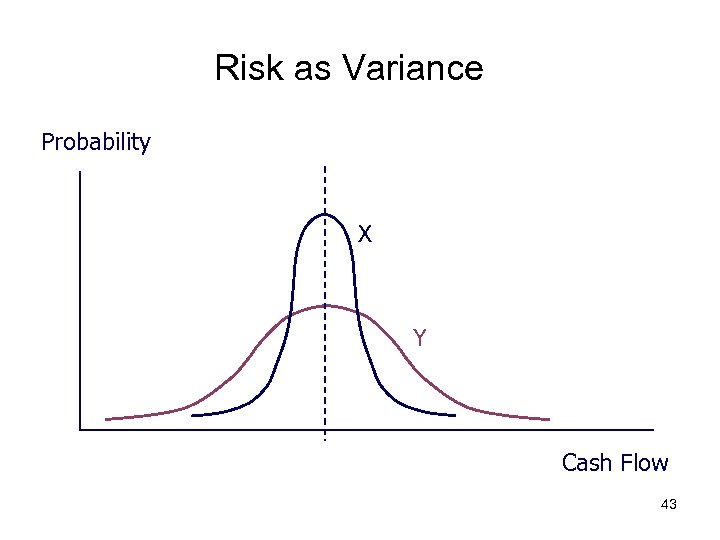Risk as Variance Probability X Y Cash Flow 43

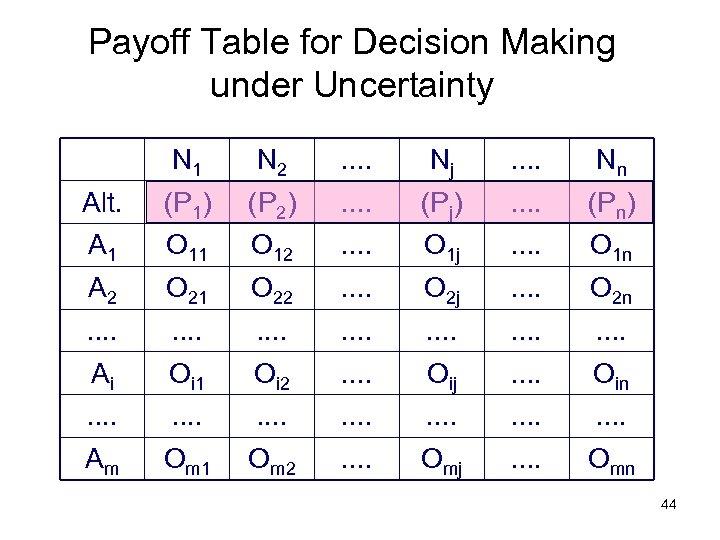Payoff Table for Decision Making under Uncertainty N 1 N 2 . . Nj . . Nn Alt. (P 1) (P 2) . . (Pj) . . (Pn) A 1 O 12 . . O 1 j . . O 1 n A 2 O 21 O 22 . . O 2 j . . O 2 n . . . . Ai Oi 1 Oi 2 . . Oij . . Oin . . . . Am Om 1 Om 2 . . Omj . . Omn 44

Tools for Decision Making under Uncertainty • • • Laplace criteria (Equally likely) Maximax criteria Maximin criteria Hurwicz criteria Minimax regret criteria Game theory 45

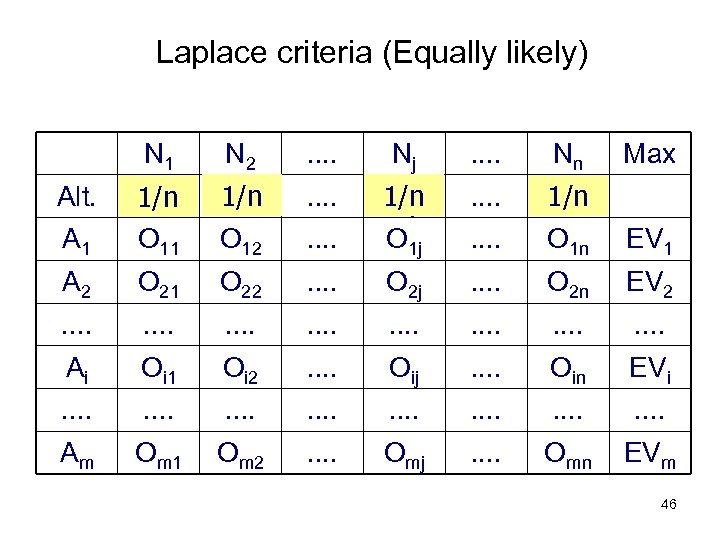Laplace criteria (Equally likely) N 1 N 2 . . Nj . . Nn Max (P 2) 1/n . . (Pj) 1/n . . A 1 (P 1) 1/n O 11 O 12 . . O 1 j . . (Pn) 1/n O 1 n EV 1 A 2 O 21 O 22 . . O 2 j . . O 2 n EV 2 . . . . Ai Oi 1 Oi 2 . . Oij . . Oin EVi . . . . Am Om 1 Om 2 . . Omj . . Omn EVm Alt. 46

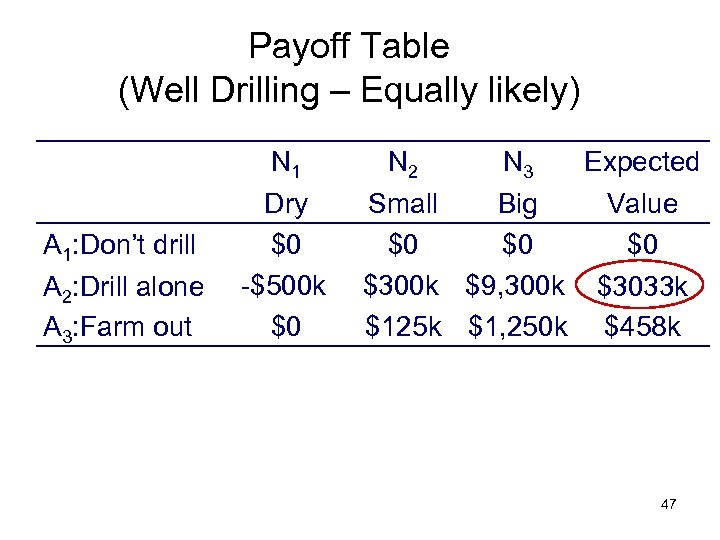Payoff Table (Well Drilling – Equally likely) A 1: Don’t drill A 2: Drill alone A 3: Farm out N 1 Dry $0 -$500 k $0 N 2 N 3 Expected Small Big Value $0 $0 $0 $300 k $9, 300 k $3033 k $125 k $1, 250 k $458 k 47

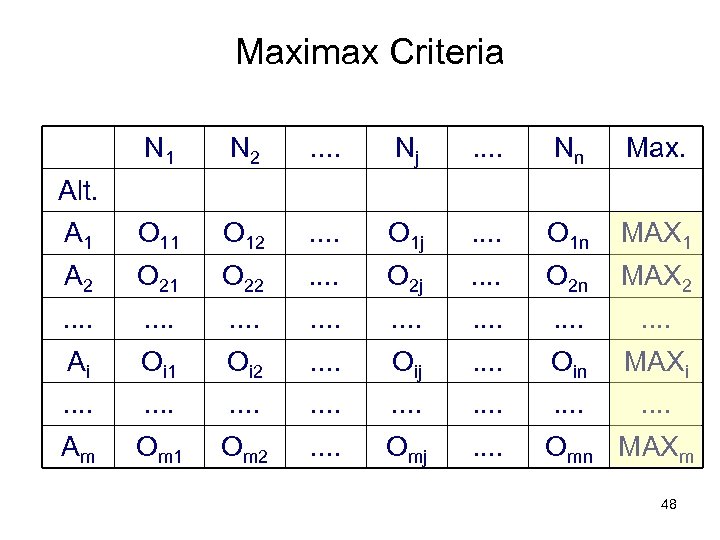Maximax Criteria N 1 N 2 . . Nj . . Nn Max. A 1 O 12 . . O 1 j . . O 1 n MAX 1 A 2 O 21 O 22 . . O 2 j . . O 2 n MAX 2 . . . . Ai Oi 1 Oi 2 . . Oij . . Oin MAXi . . . . Am Om 1 Om 2 . . Omj . . Omn MAXm Alt. 48

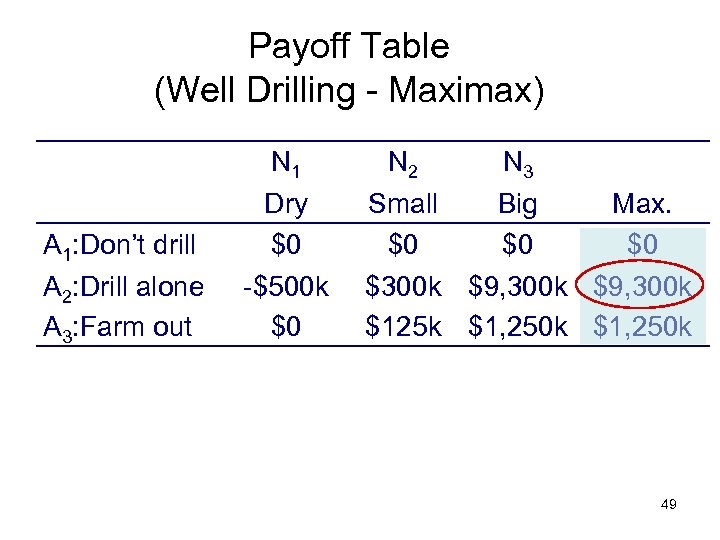Payoff Table (Well Drilling - Maximax) A 1: Don’t drill A 2: Drill alone A 3: Farm out N 1 Dry $0 -$500 k $0 N 2 N 3 Small Big Max. $0 $0 $0 $300 k $9, 300 k $125 k $1, 250 k 49

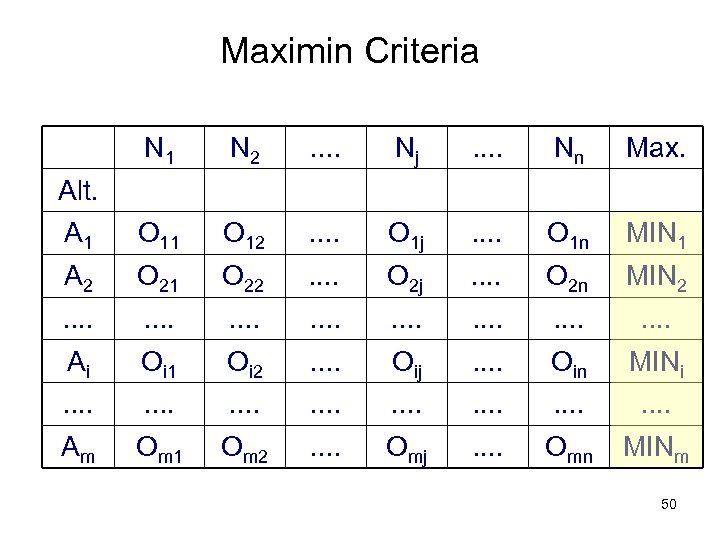Maximin Criteria N 1 N 2 . . Nj . . Nn Max. A 1 O 12 . . O 1 j . . O 1 n MIN 1 A 2 O 21 O 22 . . O 2 j . . O 2 n MIN 2 . . . . Ai Oi 1 Oi 2 . . Oij . . Oin MINi . . . . Am Om 1 Om 2 . . Omj . . Omn MINm Alt. 50

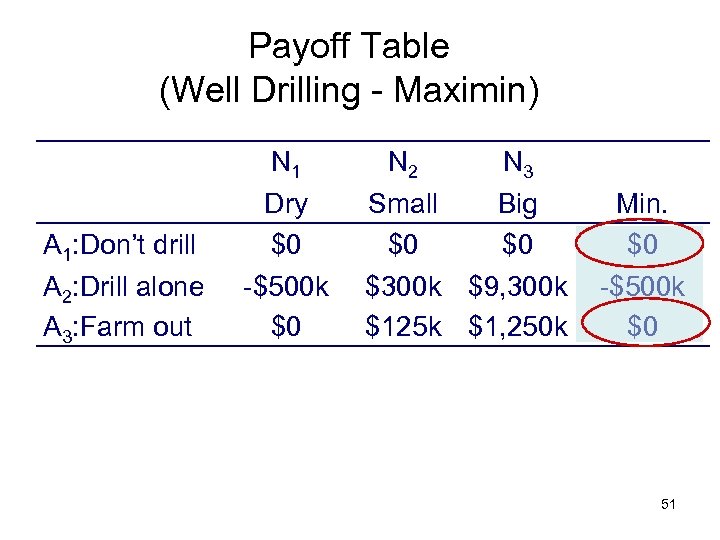Payoff Table (Well Drilling - Maximin) A 1: Don’t drill A 2: Drill alone A 3: Farm out N 1 Dry $0 -$500 k $0 N 2 N 3 Small Big $0 $0 $300 k $9, 300 k $125 k $1, 250 k Min. $0 -$500 k $0 51

Hurwicz Criteria N 1 N 2 . . Nj . . Nn (1 - ) Index Max Alt. A 1 O 12. . O 1 j. . O 1 n MAX 1 MIN 1 I 1 A 2 O 21 O 22. . O 2 j. . O 2 n MAX 2 MIN 2 I 2 . . . Ai Oi 1 Oi 2 . . Oij. . Oin . . . MAXi MINi Ii . . . Am Om 1 Om 2. . Omj. . Omn MAXm MINm Im Index = (MAX) + (1 - )(MIN) 52

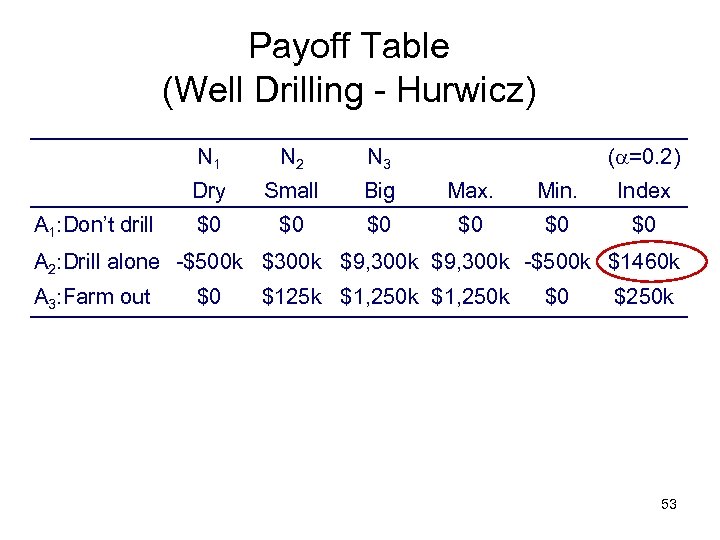Payoff Table (Well Drilling - Hurwicz) N 1 N 3 Dry A 1: Don’t drill N 2 ( =0. 2) Small Big Max. Min. Index $0 $0 $0 A 2: Drill alone -$500 k $300 k $9, 300 k -$500 k $1460 k A 3: Farm out $0 $125 k $1, 250 k $0 $250 k 53

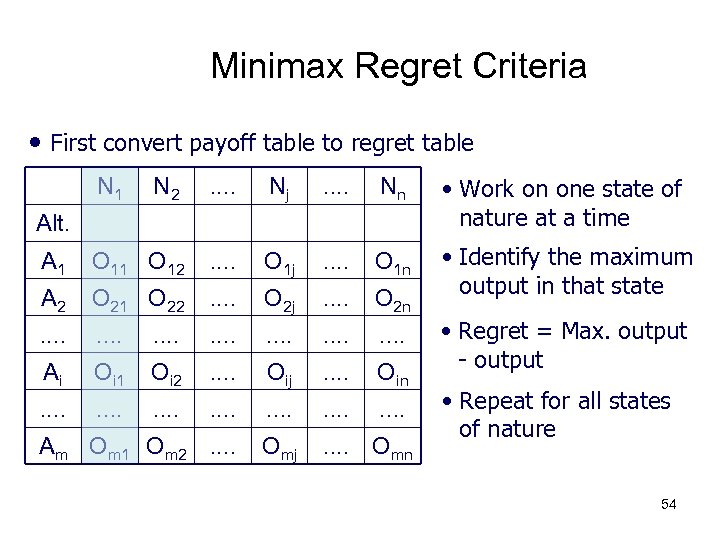Minimax Regret Criteria • First convert payoff table to regret table N 1 N 2 . . Nj . . Nn • Work on one state of nature at a time A 1 O 12 . . O 1 j . . O 1 n A 2 O 21 O 22 . . O 2 j . . O 2 n • Identify the maximum output in that state . . . . Ai Oi 1 Oi 2 . . Oij . . Oin . . . . Am Om 1 Om 2. . Omj . . Omn Alt. • Regret = Max. output - output • Repeat for all states of nature 54

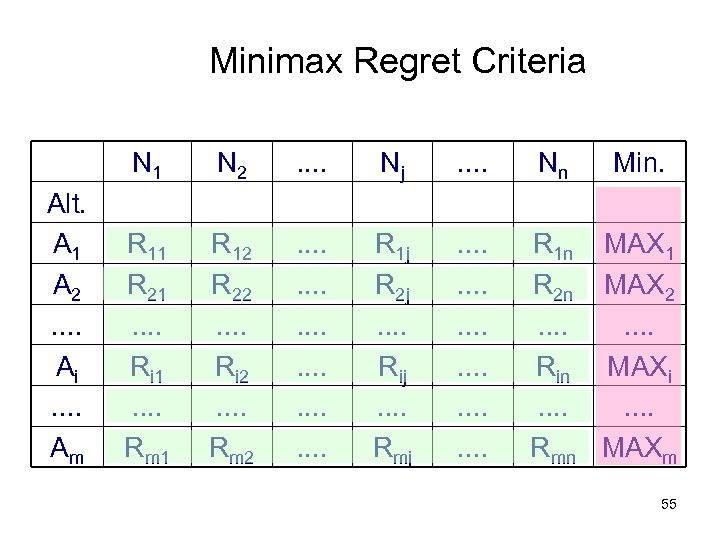Minimax Regret Criteria N 1 Alt. A 1 A 2. . Ai. . Am N 2 . . Nj . . Nn Min. R 11 R 21. . Ri 1. . Rm 1 R 12 R 22. . Ri 2. . Rm 2 . . . R 1 j R 2 j. . Rij. . Rmj . . . R 1 n MAX 1 R 2 n MAX 2. . . . Rin MAXi. . . . Rmn MAXm 55

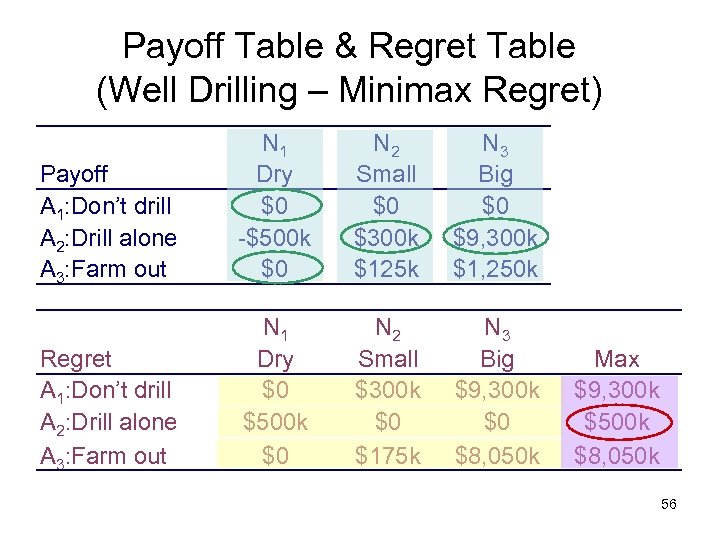Payoff Table & Regret Table (Well Drilling – Minimax Regret) Payoff A 1: Don’t drill A 2: Drill alone A 3: Farm out N 1 Dry $0 -$500 k $0 N 2 Small $0 $300 k $125 k N 3 Big $0 $9, 300 k $1, 250 k Regret A 1: Don’t drill A 2: Drill alone A 3: Farm out N 1 Dry $0 $500 k $0 N 2 Small $300 k $0 $175 k N 3 Big $9, 300 k $0 $8, 050 k Max $9, 300 k $500 k $8, 050 k 56

Game theory • Game theory attempts to mathematically capture behavior in strategic situations, where an individual’s success in making choices depends on the choices of others. • Traditional applications of game theory attempt to find equilibria in these games—sets of strategies where individuals are unlikely to change their behavior. 57

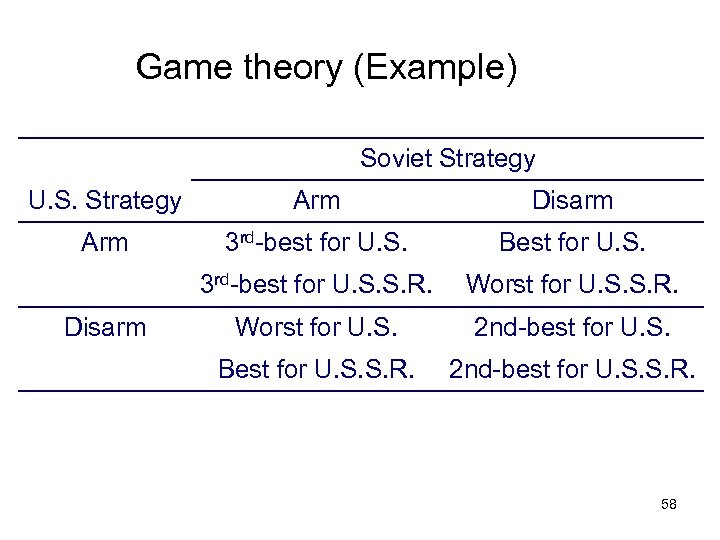Game theory (Example) Soviet Strategy U. S. Strategy Arm Disarm Arm 3 rd-best for U. S. Best for U. S. 3 rd-best for U. S. S. R. Worst for U. S. 2 nd-best for U. S. Best for U. S. S. R. 2 nd-best for U. S. S. R. Disarm 58

Computer-Based Information Systems • • • Integrated Database CAD/CAM Management Information Systems (MIS) Decision Support Systems (DSS) Expert Systems 59