4fdb072a13ef1b4f93a2997b6c10904d.ppt
- Количество слайдов: 76
 CHAPTER 4 Arrangement of Electrons in Atoms
CHAPTER 4 Arrangement of Electrons in Atoms
 Rutherford’s Model of the Atom • Electrons orbit around the nucleus like planets • What problems does this model have?
Rutherford’s Model of the Atom • Electrons orbit around the nucleus like planets • What problems does this model have?
 Limitations of Rutherford’s Model • Did not explain how the atom’s negatively charged electrons are distributed in the space surrounding its positively charged nucleus • What prevented the electrons from being drawn into the nucleus? • Led to new studies that revealed the relationship between light and an atom’s electrons
Limitations of Rutherford’s Model • Did not explain how the atom’s negatively charged electrons are distributed in the space surrounding its positively charged nucleus • What prevented the electrons from being drawn into the nucleus? • Led to new studies that revealed the relationship between light and an atom’s electrons
 Chapter 4 -1 New Development of the Atomic Model
Chapter 4 -1 New Development of the Atomic Model
 OBJECTIVES: • Identify the major regions of the electromagnetic spectrum • Describe a wave in terms of its frequency, wavelength, speed and amplitude • Explain the relationship between wavelength and frequency
OBJECTIVES: • Identify the major regions of the electromagnetic spectrum • Describe a wave in terms of its frequency, wavelength, speed and amplitude • Explain the relationship between wavelength and frequency
 Electromagnetic Radiation • A new atomic model arose out of studies of the interaction of light with matter. • There is a close relationship between light and an atom’s electrons. • Visible light is a form of electromagnetic radiation (EMR) • Form of energy • Has properties of waves and particles
Electromagnetic Radiation • A new atomic model arose out of studies of the interaction of light with matter. • There is a close relationship between light and an atom’s electrons. • Visible light is a form of electromagnetic radiation (EMR) • Form of energy • Has properties of waves and particles
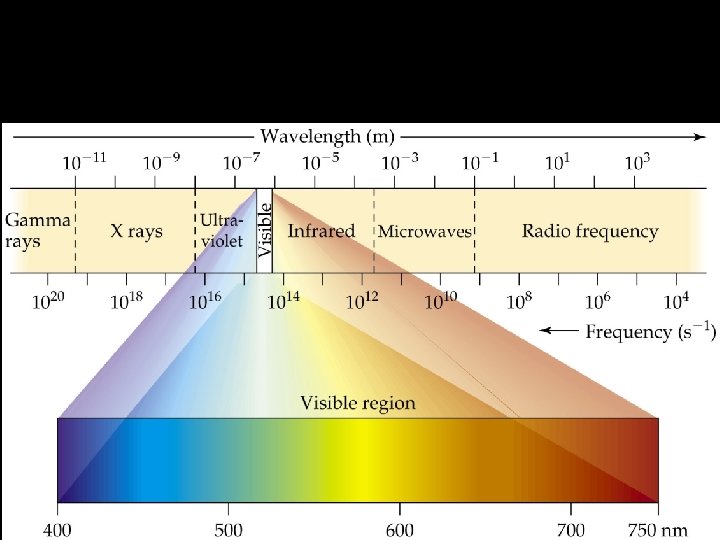
 Electromagnetic Spectrum • Composed of all the different form of EMR. • Gamma rays, x-rays, UV rays, visible light, IR, microwaves, TV waves, radio waves • Visible Light Spectrum – ROY G. BIV
Electromagnetic Spectrum • Composed of all the different form of EMR. • Gamma rays, x-rays, UV rays, visible light, IR, microwaves, TV waves, radio waves • Visible Light Spectrum – ROY G. BIV
 Speed of Light (c) • All EMR travels at the same speed - 3. 00 x 108 m/s
Speed of Light (c) • All EMR travels at the same speed - 3. 00 x 108 m/s
 Wave Properties • Described in terms of • Amplitude • Wavelength • Frequency • Speed
Wave Properties • Described in terms of • Amplitude • Wavelength • Frequency • Speed
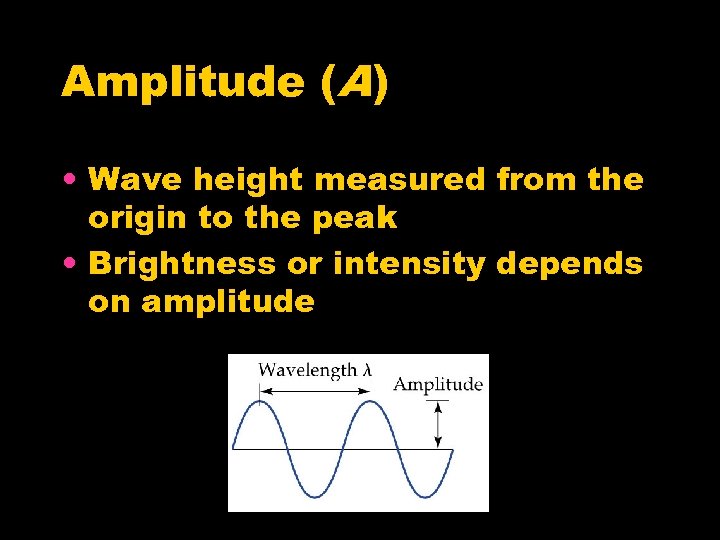 Amplitude (A) • Wave height measured from the origin to the peak • Brightness or intensity depends on amplitude
Amplitude (A) • Wave height measured from the origin to the peak • Brightness or intensity depends on amplitude
 Wavelength (λ) • The distance between two successive crests • Units of nm, cm or m
Wavelength (λ) • The distance between two successive crests • Units of nm, cm or m
 Frequency (ν) • The number of waves that pass a given point in one second • Units of Hertz (Hz) or 1/s (s-1)
Frequency (ν) • The number of waves that pass a given point in one second • Units of Hertz (Hz) or 1/s (s-1)
 Target Check • I can describe a wave in terms of its frequency, wavelength, speed and amplitude
Target Check • I can describe a wave in terms of its frequency, wavelength, speed and amplitude
 Relationship between frequency and wavelength C=λν Wavelength & frequency are inversely proportional.
Relationship between frequency and wavelength C=λν Wavelength & frequency are inversely proportional.
 Sample Problems C=λν • #1 What is the wavelength of a wave that has a frequency of 3. 4 x 1010 Hz? • #2 What is the frequency of a wave that has a wavelength of 7. 5 x 10 -17 m
Sample Problems C=λν • #1 What is the wavelength of a wave that has a frequency of 3. 4 x 1010 Hz? • #2 What is the frequency of a wave that has a wavelength of 7. 5 x 10 -17 m
 OBJECTIVES: • Explain what is meant by a quantum of energy • Describe the relationship between the energy of radiation and its wavelength • Relate the energy of radiation to its frequency • Distinguish between a continuous spectrum and a line spectrum
OBJECTIVES: • Explain what is meant by a quantum of energy • Describe the relationship between the energy of radiation and its wavelength • Relate the energy of radiation to its frequency • Distinguish between a continuous spectrum and a line spectrum
 Light as a Particle
Light as a Particle
 Photoelectric Effect • The photoelectric effect refers to the emission of electrons from the surface of a metal when light shines on the metal
Photoelectric Effect • The photoelectric effect refers to the emission of electrons from the surface of a metal when light shines on the metal
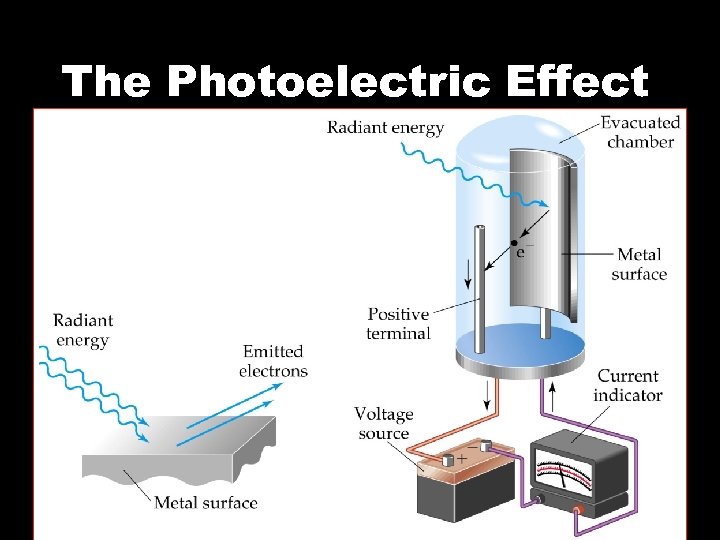 The Photoelectric Effect
The Photoelectric Effect
 Something is not quite right Up until this point, light was only considered to transfer energy in the form of waves. The amount of energy delivered depends on the amplitude of the wave. So: If we have red light and UV light both with the same amplitude, they both should knock off the same number of electrons when they shine on a metal. But this wasn’t the case.
Something is not quite right Up until this point, light was only considered to transfer energy in the form of waves. The amount of energy delivered depends on the amplitude of the wave. So: If we have red light and UV light both with the same amplitude, they both should knock off the same number of electrons when they shine on a metal. But this wasn’t the case.
 Photoelectric Effect • For each metal, there is a minimum frequency (energy) of light required to emit electrons • E. g. Red light will not emit electrons from sodium. Violet light will emit electrons from sodium. • A very intense light with too low frequency could shine on a metal forever without causing the photoelectric effect • Accounted for by particle theory
Photoelectric Effect • For each metal, there is a minimum frequency (energy) of light required to emit electrons • E. g. Red light will not emit electrons from sodium. Violet light will emit electrons from sodium. • A very intense light with too low frequency could shine on a metal forever without causing the photoelectric effect • Accounted for by particle theory
 An Analogy • If you were throwing balls at milk bottles to know them over to win a prize at a carnival, would you choose 3 baseballs or 12 table-tennis balls?
An Analogy • If you were throwing balls at milk bottles to know them over to win a prize at a carnival, would you choose 3 baseballs or 12 table-tennis balls?
 Planck’s Theory • A quantum of energy is the minimum quantity of energy that can be gained or lost by an atom.
Planck’s Theory • A quantum of energy is the minimum quantity of energy that can be gained or lost by an atom.
 Planck’s Theory • The relationship between energy and light is: where Planck’s constant (h) = 6. 626 x 10 34 J s
Planck’s Theory • The relationship between energy and light is: where Planck’s constant (h) = 6. 626 x 10 34 J s
 • Calculate the energy of a photon with a frequency of 3. 27 x 105 Hz. • Calculate the energy of a photon with a wavelength of 2. 98 x 10 -27 m.
• Calculate the energy of a photon with a frequency of 3. 27 x 105 Hz. • Calculate the energy of a photon with a wavelength of 2. 98 x 10 -27 m.
 • Einstein used Planck’s theory to explain the photoelectric effect • Assumed that electromagnetic radiation was made up of tiny energy packets (a quanta of energy) called photons that behave like tiny particles of light
• Einstein used Planck’s theory to explain the photoelectric effect • Assumed that electromagnetic radiation was made up of tiny energy packets (a quanta of energy) called photons that behave like tiny particles of light
 Dual Nature of Light • According to Einstein, light has both wave like and particle like properties • Proven in 1923 by American physicist Arthur Compton
Dual Nature of Light • According to Einstein, light has both wave like and particle like properties • Proven in 1923 by American physicist Arthur Compton
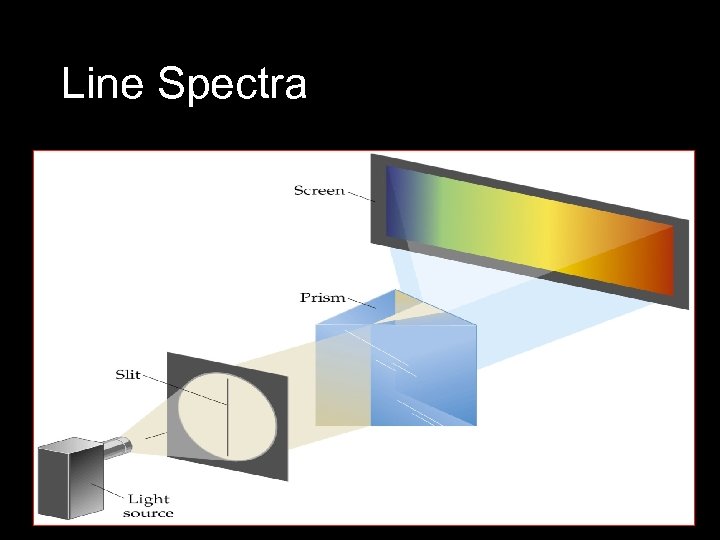
 Line Spectra • Radiation from a light source such as a light bulb can be separated into its different wavelength components. • A spectrum is then produced. • White light can be separated into a continuous spectrum of colors using a prism. • A rainbow is a continuous spectrum of light produced by dispersal of sunlight by raindrops or mist.
Line Spectra • Radiation from a light source such as a light bulb can be separated into its different wavelength components. • A spectrum is then produced. • White light can be separated into a continuous spectrum of colors using a prism. • A rainbow is a continuous spectrum of light produced by dispersal of sunlight by raindrops or mist.
 Line Spectra
Line Spectra
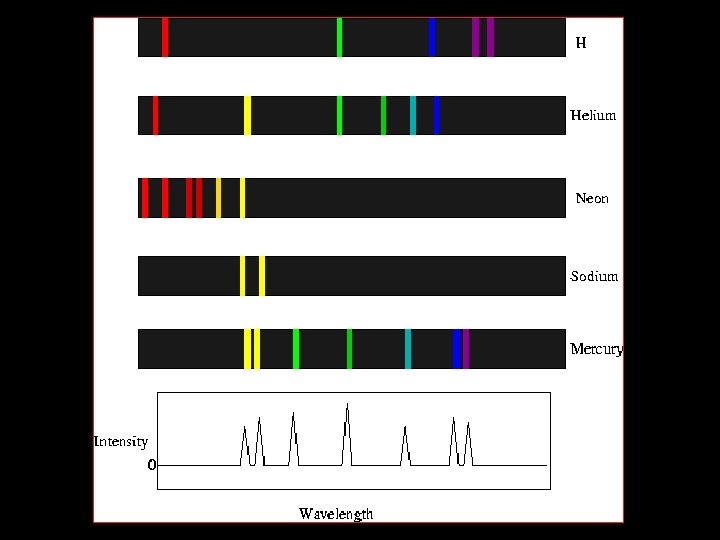
 Line Spectra • Not all radiation is continuous. • A gas placed in a partially evacuated tube and subjected to a high voltage produces single colors of light. • This single color is made up of specific wavelengths; when separated this is called a line spectrum.
Line Spectra • Not all radiation is continuous. • A gas placed in a partially evacuated tube and subjected to a high voltage produces single colors of light. • This single color is made up of specific wavelengths; when separated this is called a line spectrum.
 The Hydrogen-Atom Line -Emission Spectrum • The lowest energy state of an atom is its ground state. • A state in which an atom has a higher potential energy than it has in its ground state is an excited state. • When an excited atom returns to its ground state, it gives off energy in the form of radiation • Neon light is a familiar example
The Hydrogen-Atom Line -Emission Spectrum • The lowest energy state of an atom is its ground state. • A state in which an atom has a higher potential energy than it has in its ground state is an excited state. • When an excited atom returns to its ground state, it gives off energy in the form of radiation • Neon light is a familiar example
 OBJECTIVES: • State the main idea in Bohr’s model of the atom • Draw a Bohr model for a given element
OBJECTIVES: • State the main idea in Bohr’s model of the atom • Draw a Bohr model for a given element
 The Bohr Model Niels Bohr 1885 - 1962
The Bohr Model Niels Bohr 1885 - 1962
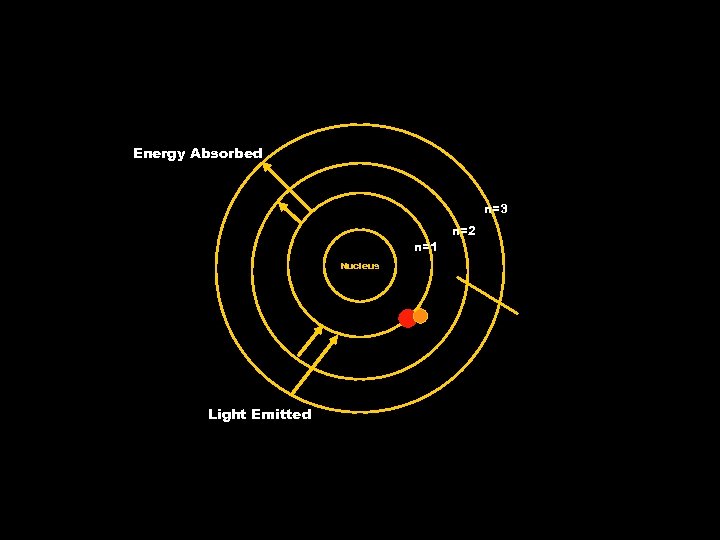
 The Bohr Model • Bohr noted the line spectra of certain elements and linked it to an atom’s electrons. • He said that the electrons were confined to specific energy states. These were called orbits. • The higher the energy state the further the orbit from the nucleus. Ground State – lowest energy state of an atom. Excited State – an energy state that has a higher potential energy than it has in its ground state
The Bohr Model • Bohr noted the line spectra of certain elements and linked it to an atom’s electrons. • He said that the electrons were confined to specific energy states. These were called orbits. • The higher the energy state the further the orbit from the nucleus. Ground State – lowest energy state of an atom. Excited State – an energy state that has a higher potential energy than it has in its ground state
 The Bohr Model • Specific line spectra arise because electrons move between orbits in the atom. • Since the energy states are quantized, the light emitted from excited atoms must be quantized and appear as line spectra.
The Bohr Model • Specific line spectra arise because electrons move between orbits in the atom. • Since the energy states are quantized, the light emitted from excited atoms must be quantized and appear as line spectra.
 The Bohr Model • Energy is only emitted or absorbed by an electron as it moves from one allowed energy state to another. • The energy is gained or lost as a photon. • Electrons that jump to higher energy levels are considered to be in an excited state
The Bohr Model • Energy is only emitted or absorbed by an electron as it moves from one allowed energy state to another. • The energy is gained or lost as a photon. • Electrons that jump to higher energy levels are considered to be in an excited state
 Energy Absorbed n=3 n=1 Nucleus Light Emitted n=2
Energy Absorbed n=3 n=1 Nucleus Light Emitted n=2
 Limitations of the Bohr Model • The Bohr Model has several limitations: • It cannot explain the spectra of atoms other than hydrogen. • Electrons do not move about the nucleus in circular orbits. • However the model introduces two important ideas: • The energy of an electron is quantized: electrons exist only in certain energy levels described by quantum numbers. • Energy gain or loss is involved in moving an electron from one energy level to another.
Limitations of the Bohr Model • The Bohr Model has several limitations: • It cannot explain the spectra of atoms other than hydrogen. • Electrons do not move about the nucleus in circular orbits. • However the model introduces two important ideas: • The energy of an electron is quantized: electrons exist only in certain energy levels described by quantum numbers. • Energy gain or loss is involved in moving an electron from one energy level to another.
 Drawing Bohr Models
Drawing Bohr Models
 4. 2 The Quantum Model of the Atom OBJECTIVES: • • State Heisenberg’s uncertainty principle. Explain constructive & destructive interference Define the 4 quantum numbers Describe atomic orbitals in terms of their shape, size and energy
4. 2 The Quantum Model of the Atom OBJECTIVES: • • State Heisenberg’s uncertainty principle. Explain constructive & destructive interference Define the 4 quantum numbers Describe atomic orbitals in terms of their shape, size and energy
 Heisenberg’s Uncertainty Principle • Heisenberg’s uncertainty principle: principle We cannot determine the exact position and speed of subatomic particles simultaneously. • For electrons: We cannot determine their momentum and position simultaneously. • Example: A mouse in a dark house
Heisenberg’s Uncertainty Principle • Heisenberg’s uncertainty principle: principle We cannot determine the exact position and speed of subatomic particles simultaneously. • For electrons: We cannot determine their momentum and position simultaneously. • Example: A mouse in a dark house
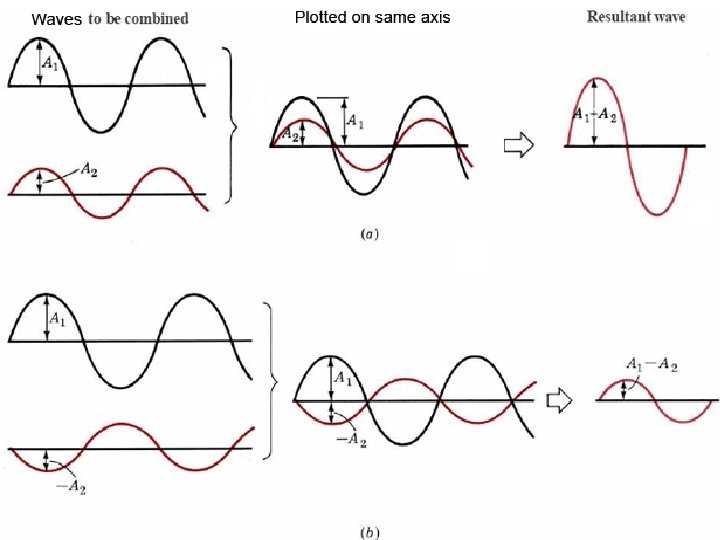
 Electrons as waves Louis de Broglie suggested the way electrons orbit the nucleus is similar to the behavior of waves. Why? Interference patterns Both light & electron beams demonstrate constructive and destructive interference.
Electrons as waves Louis de Broglie suggested the way electrons orbit the nucleus is similar to the behavior of waves. Why? Interference patterns Both light & electron beams demonstrate constructive and destructive interference.
 A New Approach to the Atom • Quantum Mechanical Model • Proposed by Schrodinger • Mathematical explanation of the properties of atoms that treats the electron as a wave and as a particle. • Describes the probability of finding an electron
A New Approach to the Atom • Quantum Mechanical Model • Proposed by Schrodinger • Mathematical explanation of the properties of atoms that treats the electron as a wave and as a particle. • Describes the probability of finding an electron
 Schrodinger’s Wave Equation • Imagine the propeller of a plane • You know the position as long as it is not moving • As the propeller moves, it now appears as a disk • Position of propeller at any instant is uncertain
Schrodinger’s Wave Equation • Imagine the propeller of a plane • You know the position as long as it is not moving • As the propeller moves, it now appears as a disk • Position of propeller at any instant is uncertain
 Orbitals • Electrons do not travel in orbits as Bohr suggested. • There are 4 sublevels ( subshells ) – s, p, d, f • Each sublevel consists of orbitals. • Orbital = 3 d region around the nucleus where an electron is most likely located • Each orbital can hold 2 electrons
Orbitals • Electrons do not travel in orbits as Bohr suggested. • There are 4 sublevels ( subshells ) – s, p, d, f • Each sublevel consists of orbitals. • Orbital = 3 d region around the nucleus where an electron is most likely located • Each orbital can hold 2 electrons
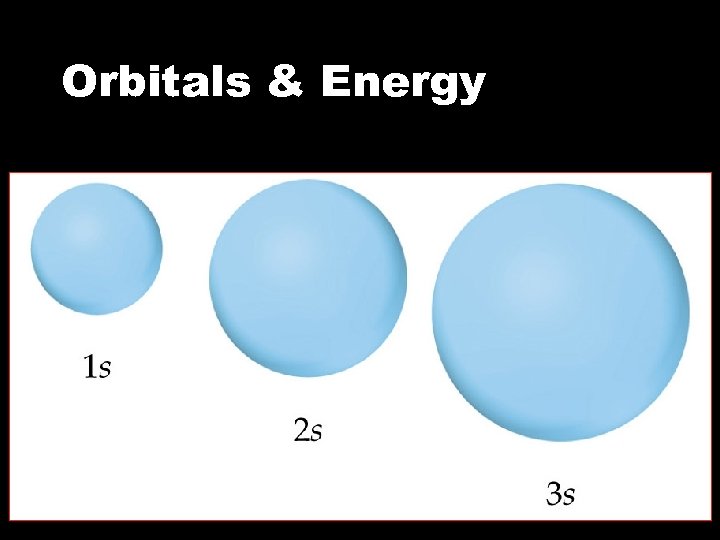
 Sub levels, Orbitals & Energy • The s sublevel • Consists of 1 orbital • All s orbitals are spherical • As energy level ( n ) increases, the orbitals get larger s
Sub levels, Orbitals & Energy • The s sublevel • Consists of 1 orbital • All s orbitals are spherical • As energy level ( n ) increases, the orbitals get larger s
 Orbitals & Energy
Orbitals & Energy
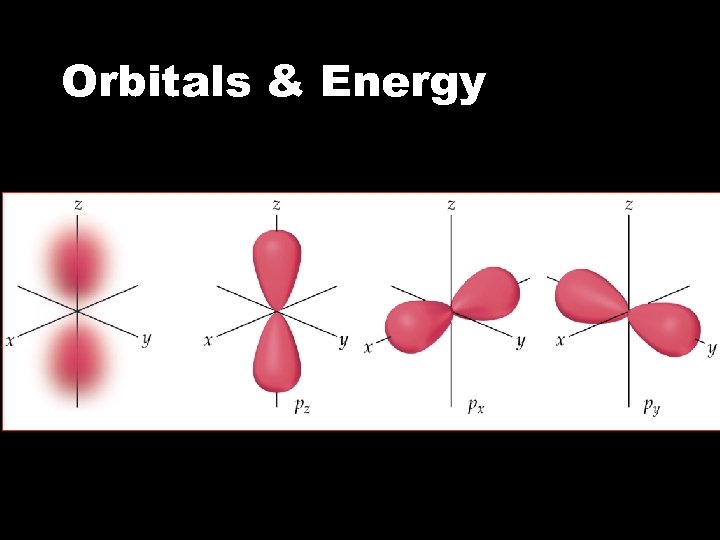
 Orbitals & Energy • The p sublevel • There are three p orbitals px, py, and pz • The orbitals are dumbbell shaped • As n increases, the p orbitals get larger
Orbitals & Energy • The p sublevel • There are three p orbitals px, py, and pz • The orbitals are dumbbell shaped • As n increases, the p orbitals get larger
 Orbitals & Energy
Orbitals & Energy
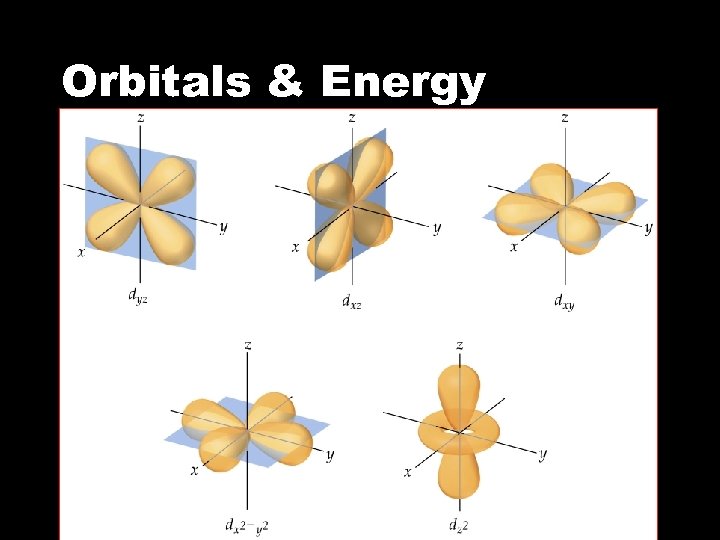
 Orbitals & Energy • The d sublevel • There are five d orbitals • Four of the d orbitals have four lobes each • One d orbital has two lobes and a collar
Orbitals & Energy • The d sublevel • There are five d orbitals • Four of the d orbitals have four lobes each • One d orbital has two lobes and a collar
 Orbitals & Energy
Orbitals & Energy
 Orbitals & Energy • The f sublevel • There are 7 f orbitals All sublevels in the same energy level together make up a shell.
Orbitals & Energy • The f sublevel • There are 7 f orbitals All sublevels in the same energy level together make up a shell.
 Orbitals & Energy
Orbitals & Energy
 Quantum Numbers • Identify an approx. location of an electron • Specify the properties of the atomic orbital and properties of the electrons in that orbital • There are 4 quantum numbers. • “Address” of the electron
Quantum Numbers • Identify an approx. location of an electron • Specify the properties of the atomic orbital and properties of the electrons in that orbital • There are 4 quantum numbers. • “Address” of the electron
 Quantum Numbers, con’t • Principal Quantum Number, n. • Indicates the main energy level, n = 1, 2, 3… • As n becomes larger, the atom becomes larger and the electron is further from the nucleus. • The total number of orbitals that exist in a given shell, or main energy level, is equal to n 2.
Quantum Numbers, con’t • Principal Quantum Number, n. • Indicates the main energy level, n = 1, 2, 3… • As n becomes larger, the atom becomes larger and the electron is further from the nucleus. • The total number of orbitals that exist in a given shell, or main energy level, is equal to n 2.
 Quantum Numbers, con’t • Angular Quantum Number, l • Describes the shape of the orbital (s, p, d, or f) • This quantum number depends on the value of n. • The values of l begin at 0 and increase to (n 1). • l=0=s l=1=p l=2=d l =3 = f Example: If n = 2 ; then l = 0, 1
Quantum Numbers, con’t • Angular Quantum Number, l • Describes the shape of the orbital (s, p, d, or f) • This quantum number depends on the value of n. • The values of l begin at 0 and increase to (n 1). • l=0=s l=1=p l=2=d l =3 = f Example: If n = 2 ; then l = 0, 1
 Quantum Numbers, con’t • Magnetic Quantum Number, ml • This quantum number depends on l • The magnetic quantum number has integral values between l and +l • Magnetic quantum numbers give the 3 D orientation of each orbital. ( x, y, z axis ) Example: If n = 2 and l = 0, 1; then m = 1, 0, +1
Quantum Numbers, con’t • Magnetic Quantum Number, ml • This quantum number depends on l • The magnetic quantum number has integral values between l and +l • Magnetic quantum numbers give the 3 D orientation of each orbital. ( x, y, z axis ) Example: If n = 2 and l = 0, 1; then m = 1, 0, +1
 Quantum Number, con’t • Spin Quantum Number, ms • Indicates the direction of spin of the electron in the orbital • Only two possible values, ½ OR +½
Quantum Number, con’t • Spin Quantum Number, ms • Indicates the direction of spin of the electron in the orbital • Only two possible values, ½ OR +½
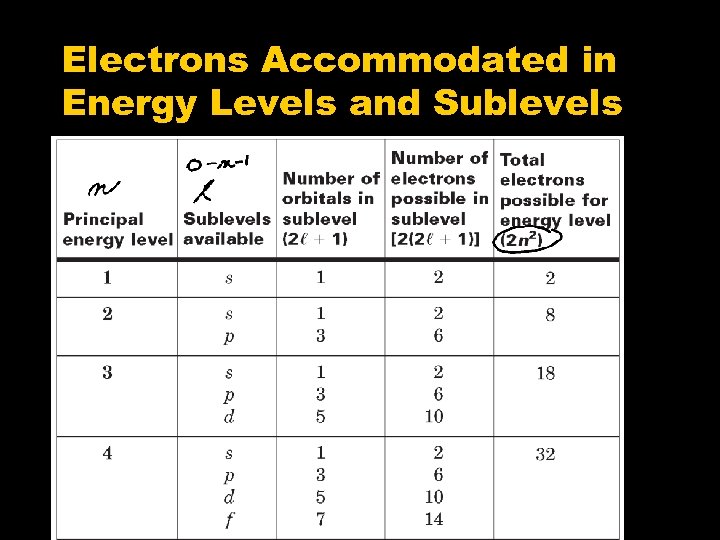 Electrons Accommodated in Energy Levels and Sublevels
Electrons Accommodated in Energy Levels and Sublevels
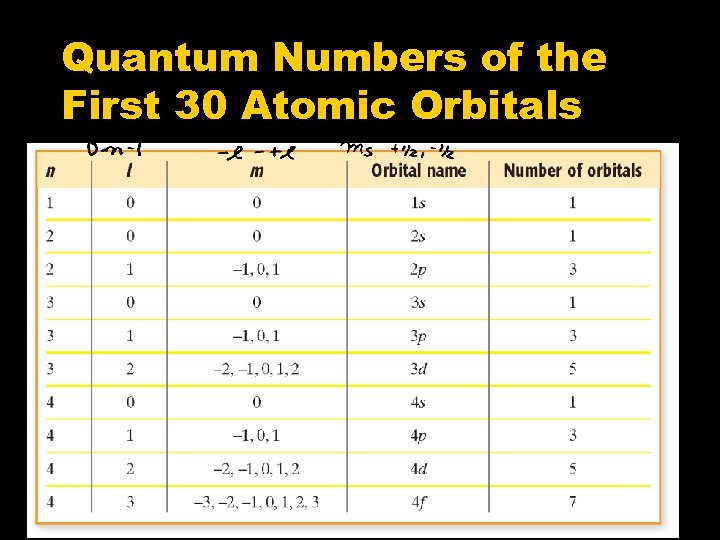 Quantum Numbers of the First 30 Atomic Orbitals
Quantum Numbers of the First 30 Atomic Orbitals
 4. 3 Electron Configurations OBJECTIVES: • Write out an electron configuration for an element. • Write out an orbital notation for an element. • Write out a noble gas notation for an element. • State & use Aufbau principle, Pauli exclusion principle, and Hund’s rule.
4. 3 Electron Configurations OBJECTIVES: • Write out an electron configuration for an element. • Write out an orbital notation for an element. • Write out a noble gas notation for an element. • State & use Aufbau principle, Pauli exclusion principle, and Hund’s rule.
 Electron Configurations Shows the arrangement of electrons within an atom. There are 3 different methods for writing electron configurations Each element has a unique electron configuration.
Electron Configurations Shows the arrangement of electrons within an atom. There are 3 different methods for writing electron configurations Each element has a unique electron configuration.
 Rules for electron configurations Aufbau Principle – electrons occupy the lowest energy orbital it can Hund’s Rule – each orbital is occupied by 1 electron before a second electron can be added Pauli Exclusion Principle – no 2 electrons can have the same 4 quantum numbers. Therefore electron within an orbital must have opposite spins.
Rules for electron configurations Aufbau Principle – electrons occupy the lowest energy orbital it can Hund’s Rule – each orbital is occupied by 1 electron before a second electron can be added Pauli Exclusion Principle – no 2 electrons can have the same 4 quantum numbers. Therefore electron within an orbital must have opposite spins.
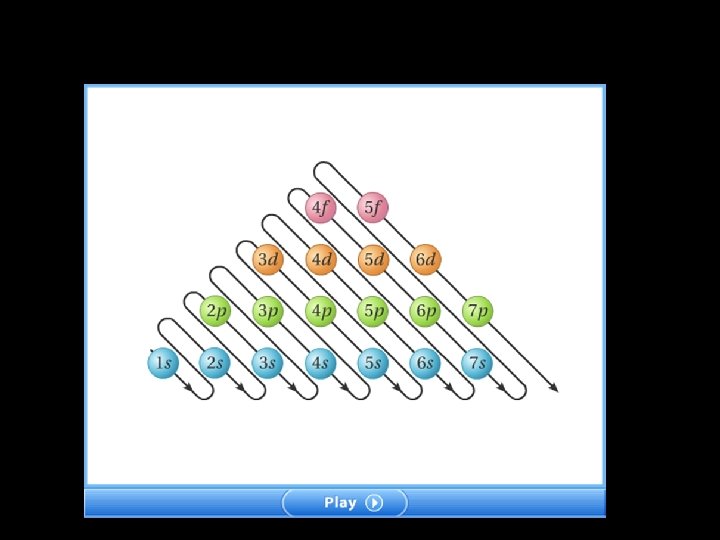
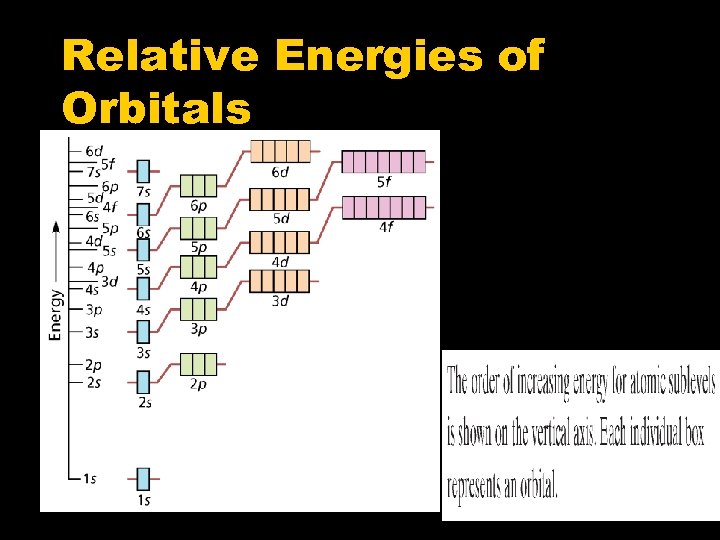 Relative Energies of Orbitals
Relative Energies of Orbitals
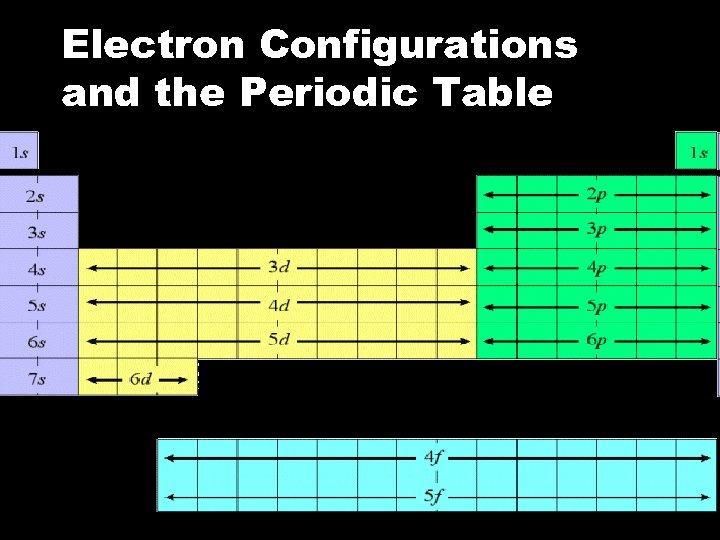 Electron Configurations and the Periodic Table
Electron Configurations and the Periodic Table
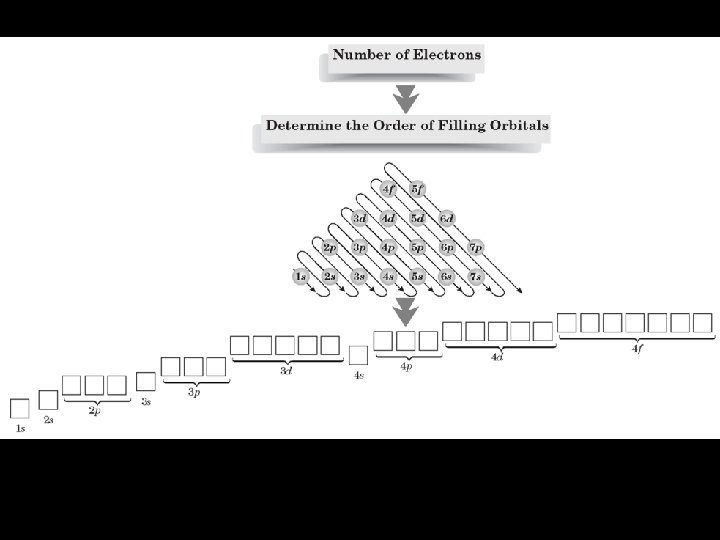
 Orbital Notation Lines = orbitals Arrows = electrons EXCEPTION TO THE RULES: ½ filled orbitals are more stable than partially filled orbitals. Example: Cr, Cu Orbital notation for: Oxygen, Aluminum, Argon, Copper
Orbital Notation Lines = orbitals Arrows = electrons EXCEPTION TO THE RULES: ½ filled orbitals are more stable than partially filled orbitals. Example: Cr, Cu Orbital notation for: Oxygen, Aluminum, Argon, Copper
 • Oxygen • Aluminum • Argon • Copper
• Oxygen • Aluminum • Argon • Copper
 Electron Configuration Notation Eliminates lines & arrows. It uses numbers and letters to represent energy levels, type of orbital, and number of electrons. By following the organization of the periodic table we can correctly write electron configurations.
Electron Configuration Notation Eliminates lines & arrows. It uses numbers and letters to represent energy levels, type of orbital, and number of electrons. By following the organization of the periodic table we can correctly write electron configurations.
 Electron Configuration of Al:
Electron Configuration of Al:
 Noble Gas Notation • Shorter way to write electron configuration • Generally accepted way • Ex: Al
Noble Gas Notation • Shorter way to write electron configuration • Generally accepted way • Ex: Al
 What about ions? • Calculate number of electrons and use the same method as with atoms. • Ex. Ca+2
What about ions? • Calculate number of electrons and use the same method as with atoms. • Ex. Ca+2


