Chapter 4 堆疊與佇列的應用學習目標 n 在學習本章之後讀者們要能夠瞭解 n

Chapter 4 堆疊與佇列的應用

學習目標 n 在學習本章之後，讀者們要能夠瞭解： n 1. 堆疊與佇列在電腦程式上實際應用。 n 2. 如何利用堆疊與佇列解決河內塔問題。 n 3. 如何利用堆疊與佇列設計老鼠走迷宮的程式。 n 4. 佇列 (Queue)在電腦硬體執行效率的應用說明

堆疊在計算機上的應用 n 副程式的呼叫： n 在呼叫副程式之前，須先將一條指令的位址，亦即返回位址保存到堆疊中當爾後副程式執行完時，再從堆疊頂端取出返回位址，回到原來執行時的下一指令位址繼續往下執行。 n 處理遞迴式呼叫叫： n 與副程式類似，在每次遞迴之前，須先將下一條指令的位址，暫存器及變數的值保存到堆疊中，當爾後遞迴回來時，能再從堆疊頂端取出暫存值，回到原來執行遞迴前狀況，並從下一指令繼續往下執行。 n 算術式之轉換： n 在編譯程式時，堆疊可幫助分析指令，以判斷某一個指令是否合法；此外，算術運算時，利用堆疊的特性將不同的算術式表示法轉換，以利算術式的執行。 n 二元樹的追蹤： n 如中序及前序追蹤以及圖形的深入追蹤。 n 中斷處理(Intrrupt Handing) n 迷宮問題

佇列的結構在計算機上的應用 n 作業系統的作排序 n 計算機的作業系統裡，若所有的作優先權 (Proiority) 都相同，則可採用佇列來安排作排程 (Job Scheduling)，使其達到先到先做的特性。 n 用於印表機或作業系統的Spooling n 做為輸出入作緩衝區 (Buffer)，例如印表機的pooling即是將輸入資料寫在磁碟上，再輸入電腦記憶體內處理，處理後的輸出資料亦先寫在磁碟上，再由印表機印出，亦是採用佇列的特性來完成。 n 計算機的模擬(Simulation) n 模擬是一種評估的技術，評估者建立一套電腦化系統評估模式將真實情況藉由一種抽象模式，以分析、瞭解各種因素的影響；而在模擬的過程中，常有事件趨勢 (Event-Driven) 或時間趨動 (Time-Driven) 的輸入訊號，由於其輸入時間不一，因此使用佇列來反映真實的情況。 n 資料通訊中，一般均是先傳送的資料先接收到，後傳送的資料後接收到，亦是採用佇列的特性來完成。

堆疊之應用副程式及遞迴之呼叫

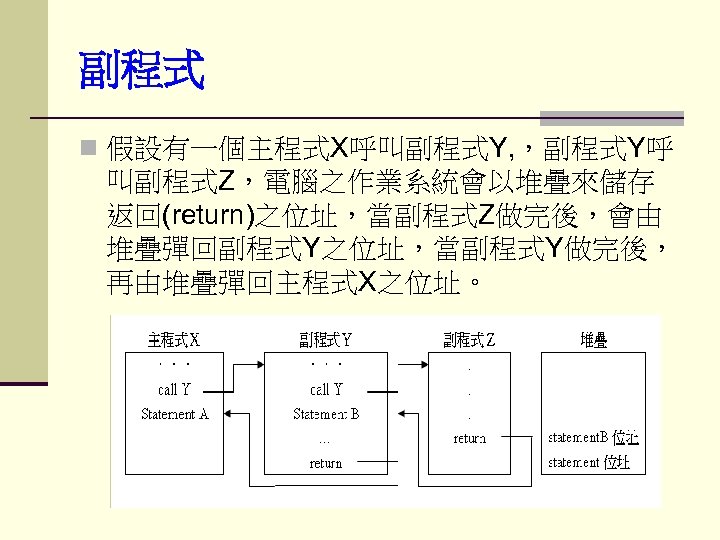
副程式 n 假設有一個主程式X呼叫副程式Y, ，副程式Y呼叫副程式Z，電腦之作業系統會以堆疊來儲存返回(return)之位址，當副程式Z做完後，會由堆疊彈回副程式Y之位址，當副程式Y做完後，再由堆疊彈回主程式X之位址。

遞迴(Recursion) n 一個函式呼叫自己本身，且至少要定義 2種條件 n 如何開始 n 如何結束遞迴 n C語言的函數可進行遞迴呼叫(recursive call) n 就是說在函數之中可呼叫函數本身。 n 函數在進行遞迴呼叫時，在其所使用的變數被堆積在堆疊區域，每次執行return敘述，函數在該層呼叫中所使用的變數就從堆疊返回。

程式實例 #include <stdio. h> void printer(int); void main() { printer(5); } void printer(int count) { if (count) { printf("%d, ", count); printer(--count); printf("%d, ", count); } }

遞迴(Recursion)範例（一）最大公因數

演算流程 n 計算最大公因數，可以使用輾轉相除法 n 在電腦程式處理上，則可以使用遞迴來達到目的 n 使用遞迴前，必須定義兩件事情： n 什麼情況下作遞迴： n 在餘數不為 0時，則原來的除數為新函式的被除數，而原函式的餘數為新函式除數。 n 什麼情況下作遞迴結束： n 在餘數為 0時，表示除數為答案，即可結束。 n 由以上分析，可將GCD(a, b)定義如下：: 當b = 0時，傳回a

C語言：程式碼 #include <stdio. h> int GCD(int, int); void main() { int a, b; printf("Pleace input a: "); scanf("%d", &a); printf("Pleace input b: "); scanf("%d", &b); printf("GCD(%d, %d) = %d", a, b, GCD(a, b)); } int GCD(int a, int b) { if (b) { return (GCD(b, a%b)); // 當b非 0時做GCD(b, a%b) } else { return (a); // 當b為 0時傳回a } }

遞迴(Recursion)範例（二）費氏級數

定義 n 費波納奇數列是 13世紀一個數學家費波納奇發現的 n 可以用的範圍很多 n 比方說藝術上的黃金比率、, 建築設計、甚至艾略特波浪理論(使用費氏級數對股票波動進行分析)。 n 在電腦程式的處埋上，同樣的可以使用遞迴來表達費氏級數的運算原理。.

C語言：程式碼 #include <stdio. h> float fib(int); void main() { int number; printf("pleace input a number: "); scanf("%d", &number); printf("The fib(%d) = %g", number, fib(number )); } float fib(int number) { if (number <= 2) { return 1; } else { return (fib(number-2) + fib(number-1)); } }

遞迴(Recursion)範例（三） N階乘

演算流程 n 階乘的意義如下: n 1! = 1 n 2! = 1! * 2 = 1 * 2 = 2 n 3! = 2! * 3 = 1! * 2 * 3 = 1 * 2 * 3 = 6 n. . . (以此類推) n 設函式名稱為factor ( int n)： n 當N為 1時，執行factor(1)傳回 1。

C語言：程式碼 #include <stdio. h> float factor(int); void main() { int n; printf("Pleace input a number: "); scanf("%d", &n); printf("The %d! is %g", n, factor(n)); } float factor(int n) { if (n == 1) // 當n為 1時傳回 1 { return 1; } else { return (n * factor(n-1)); // 當n不為 1時傳回n * factor(n-1) } }

遞迴(Recursion)範例（四）八皇后問題

n 八皇后問題是說明在一個８＊８的棋盤上面，要將8個皇后都放上去，但每個皇后之間不能有相互攻擊的現象。 n 所謂不相互攻擊就是不能有兩個皇后放在同一列、同一行或者是對角線上 n 現在可用遞迴方式來完成，我們稱之為回溯法 (BACKTRACKING)

演算流程 #include <stdio. h> #include <conio. h> int crosscheck(int , int) ; int verticalcheck(int , int) ; int safe(int , int) ; void print(int [][8]) ; void tryrow(int) ; static int q[8][8] ; static cnt = 0 ;

int main(void) { int i , j ; for(i = 0 ; i <= 7 ; i++) for(j = 0 ; j <= 7 ; j++) q[i][j] = 0 ; tryrow(0) ; return 0 ; }

n n n int crosscheck(int x , int y) { int i , j ; i = x ; j = y ; while( (i > 0) && (j > 0) ) { i -= 1 ; j -= 1 ; if(q[i][j]) return 0 ; }

i = x ; j = y ; while( (i < 7) && (j > 0) ) { i += 1 ; j -= 1 ; if(q[i][j]) return 0 ; } return 1 ; }

int verticalcheck(int x , int y) { while(y > 0) { y -= 1 ; if(q[x][y]) return 0 ; } return 1 ; }

n int safe(int x , int y) { return( crosscheck(x, y) && verticalcheck(x, y) ) ; }

void print(int a[8][8]) { int i , j ; clrscr() ;

gotoxy(21, 4) ; printf("I----------------I") ; gotoxy(21, 5) ; printf("I I I") ; gotoxy(21, 6) ; printf("I---+---+---+---+---I") ; gotoxy(21, 7) ; printf("I I I") ; gotoxy(21, 8) ; printf("I---+---+---+---+---I") ; gotoxy(21, 9) ; printf("I I I") ; gotoxy(21, 10) ; printf("I---+---+---+---+---I") ; gotoxy(21, 11) ; printf("I I I") ; gotoxy(21, 12) ; printf("I---+---+---+---+---I") ; gotoxy(21, 13) ; printf("I I I") ; gotoxy(21, 14) ; printf("I---+---+---+---+---I") ; gotoxy(21, 15) ; printf("I I I") ; gotoxy(21, 16) ; printf("I---+---+---+---+---I") ; gotoxy(21, 17) ; printf("I I I") ; gotoxy(21, 18) ; printf("I---+---+---+---+---I") ; gotoxy(21, 19) ; printf("I I I") ; gotoxy(21, 20) ; printf("I----------------I") ;

for( i = 0 ; i <= 7 ; i++ ) for( j = 0 ; j <= 7 ; j++ ) if(a[i][j]) { gotoxy(i * 4 + 23 , j * 2 + 5) ; printf("Q") ; } gotoxy(32, 22) ; printf("count = %d", cnt) ; }

void tryrow(int row) { int column = 0 ; do { if(safe(column , row)) { q[column][row] = 1 ; if(row < 7) tryrow(row + 1) ; else { cnt += 1 ; print(q) ;

if(getch() == 0) { getch() ; clrscr() ; exit(0) ; } } q[column][row] = 0 ; } column += 1 ; }while(column < 8) ; }

堆疊之應用代數運算式的求值計算

表示法 n 一般計算機或電腦運算中，常用的四則運算有三種表示方式：中序法 n 前序法 n 後序法。 n n 後序法為電腦最常使用的運算方式

後序運算式之計算表示法 n 規則如下： n 由左而右讀進後序運算式的每個字元(Token)

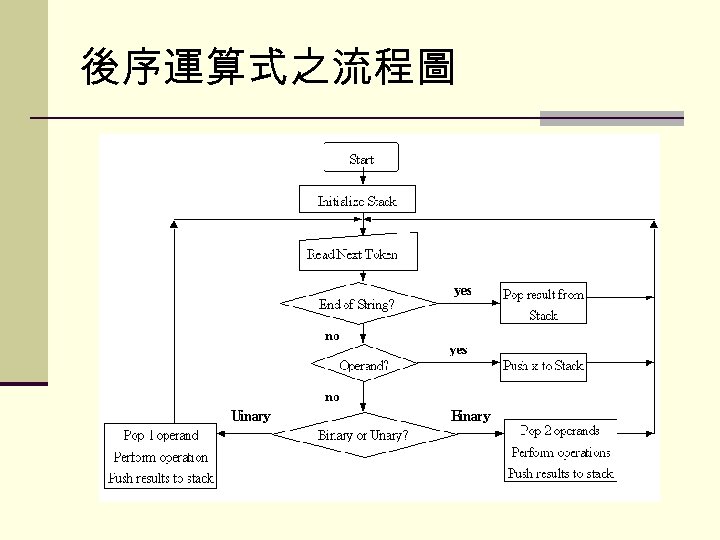
後序運算式之流程圖

C語言：程式碼 # include <stdio. h> # include <math. h> # include <ctype. h> # include <stdlib. h> /* 陣列堆疊宣告 */ #define N 100 int stack[N];

//*********************************** //* push函式部分 ( stack〔〕　宣告為全域變數 ) //*********************************** void push(int d, int *top ) /*此處之top為一指標型區域變數*/ { if (*top == N-1) { printf("堆疊滿了n"); /* 注意堆疊大小*/ exit(1); /* exit定義在stdlib. h中 */ /* exit(0)表示正常，exit(1) 表示有誤*/ } /* end if */ else { (*top)++; /*指標指向頂端，增量增加 1*/ stack[*top]=d; /*儲存資料d 於堆疊頂端*/ } /* end else */ } /* end of push 函數 */

//************************************ //*pop函式部分 ( stack〔〕　宣告為全域變數 ) * //************************************ int pop(int *top) { if (*top == -1) /* 注意空堆疊情形*/ { printf("堆疊空了n"); exit(1); /*刪除失敗，執行結束*/ } else return(stack[(*top)--]); }

//************************************** //* oper函數 ( 檢查有效二元運算子，並計算該運算運用在其後兩參數之結果) * //************************************** double oper(int symb, double op 1, double op 2) { switch (symb) { case ‘+’ : return (op 1+op 2); /* 相加運算 */ case ‘-’ : return (op 1 -op 2); /* 相減運算 */ case ‘*’ : return (op 1*op 2); /* 相乘運算 */ case ‘/’ : return (op 1/op 2); /* 相除運算 */ case ‘$’ : return (pow(op 1, op 2))； /*次方運算, pow定義在math. h 中*/ default : printf(“%s”, “illegal operation”); exit(1); /* 加入失敗，執行結束*/ } /* end switch*/ } /* end oper函數 */

$//********************************* //* eva_postfix函數 (計算後序運算式值) //********************************* double eval_postfix(char expr[ ]) { int c, position; double$

//********************************* //* eva_postfix函數 (計算後序運算式值) //********************************* double eval_postfix(char expr[ ]) { int c, position; double opnd 1, opnd 2, value; top = -1; /* initialize stack*/ for (position = 0; (c = expr[position]) != ‘’; position++) /*將儲存後序運算式從頭到尾依序讀出*/ /*字串之 ‘’　為字串終止控制指令*/ if (isdigit(c)) 　/* 將自十進位數值字元轉換為可計算之double */ /*isdigit(c)　函數定義在　ctype. h 中*/ push( (double)(c –‘ 0’), &top); /* c - ‘ 0’ 會將字元變數 c 之ASCII碼減去字元 ’ 0’ 之ASCII碼 */ else { /* 此時讀進之字元為　operator*/ opnd 2 = pop(&top); opnd 1 = pop(&top); /* 取出堆疊最頂端的兩個運算元*/ value = oper(c, opnd 1, opnd 2); /* 並執行運算子所對應之計算*/ push(value, &top); /*將計算結果放入堆疊中*/ } /* end else*/ return (pop(&top)); /* 傳回堆疊內唯一值*/ } /* end eval_postfix*/

//********************************* //* 主程式部分 //********************************* void main() { char expr[N]; int position = 0; while ((expr[position++] = getchar()) != ‘n’ ) ﹔ /*getchar()函數定義在ctype. h 中 */ /*從系統開啟檔案或鍵盤中讀取單一字元*/ expr[--position] = ‘’; printf (“n %s %s “, “ the original postfix expression is “, expr); /*列印原始後序運算式*/ printf(“ n %f”, eval_postfix(expr)); /*列印計算後之計算值*/ } /* end main*/

堆疊之應用中序運算式轉換為後序運算式

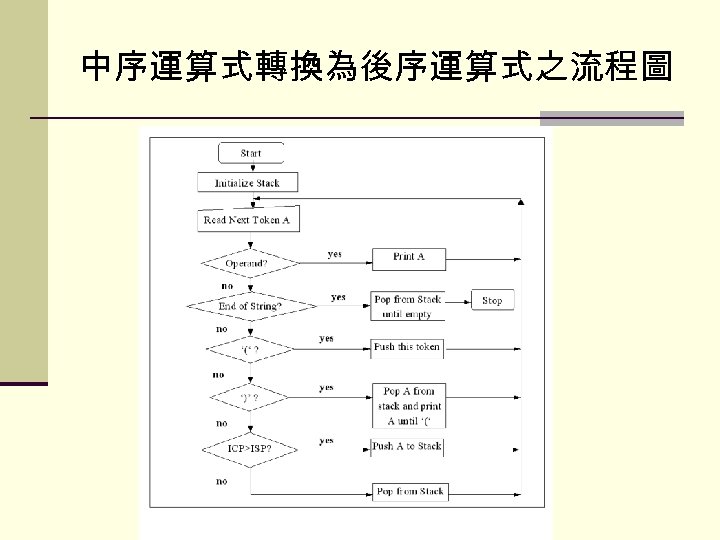
中序運算式轉換為後序運算式之流程圖

$C語言：程式碼 //【變數宣告部分】 #define N 100 /* N為全域變數 */ typedef enum{left_paren, right_paren, plus, minus, times,$

C語言：程式碼 //【變數宣告部分】 #define N 100 /* N為全域變數 */ typedef enum{left_paren, right_paren, plus, minus, times, divide, mode, operand} precedence; /* 定義優先順序之資料型態 */ precedence stack[N]; int ISP[]= {1, 4, 2, 2, 3, 3, 3, 0}; /* 定義堆疊頂端之優先權 */ int ICP[]= {5, 4, 2, 2, 3, 3, 3, 0}; /* 定義 Token之優先權 */

$//【get_token 函數】 (讀取字元Token，並按照其優先順序分類) precedence get_token (char token) { switch (token) /* 將讀進之Token 量化並分類$

//【get_token 函數】 (讀取字元Token，並按照其優先順序分類) precedence get_token (char token) { switch (token) /* 將讀進之Token 量化並分類 */ { case '(' : return left_paren; /* 此時 '(' 等於left_paren = 0 */ case ')' : return right_paren; /* 此時 ')'等於 right_paren = 1 */ case '+' : return plus; /* 依此類推 */ case '-' : return minus; case '*' : return times; case '/' : return divide; case '%' : return mode; default : return operand; } /* end switch*/ } /* end get_token 函數 */

$//【infix_to_postfix函數】 (將中序式轉換為計後序運算式) void infix_to_postfix(char expr[]) { int position=0; /*目前讀取位元之位置 */ char c;$

//【infix_to_postfix函數】 (將中序式轉換為計後序運算式) void infix_to_postfix(char expr[]) { int position=0; /*目前讀取位元之位置 */ char c; /* 讀取一個字元 */ precedence token; /* 分類後之token */ top = -1; /* initialize stack */

for (position = 0; (c = expr[position]) != ''; position++) /*將儲存中序運算式從頭到尾依序讀出*/ /*字串之 ''　為字串終止控制指令*/ { token = get_token(c); /* 讀取一個字元*/ switch (token) { case operand : /* 此時 token 為運算元*/ printf("%c", c); break;

$case right_paren : while(stack[top] != left_paren) /*自堆疊頂端逐一取出並輸出，直到取出 '('為止*/ { print_symbol(stack[top]); pop(&top); /*移除堆疊頂端之'(', 不須印出*/ }$

case right_paren : while(stack[top] != left_paren) /*自堆疊頂端逐一取出並輸出，直到取出 '('為止*/ { print_symbol(stack[top]); pop(&top); /*移除堆疊頂端之'(', 不須印出*/ } /* end while */ break; default: if (empty(&top)) /* empty stack, push the token directly */ push(token, &top); else { while ((!empty(&top)) && (ISP[stack[top]] >= ICP[token])) print_symbol(pop(&top)); push(token, &top); /* push token to stack */ } /* end else */ } /* end switch */ } /* end for */

do { /* end of string , pop from stack until empty */ token = pop(&top); print_symbol(token); } while (!empty(&top)); } /* end infix_to_postfix */ p. s ＞empty 及 print_symbol 函數須自行定義

Chapter 4 堆疊與佇列的應用 學習目標 n 在學習本章之後 讀者們要能夠瞭解 n

Chapter 4 堆疊與佇列的應用學習目標 n 在學習本章之後讀者們要能夠瞭解 n