9bed02e685048eea3bc32e374d70c53f.ppt
- Количество слайдов: 34

Chapter 36 Public Goods

Public Goods -- Definition n A good is purely public if it is both nonexcludable and nonrival in consumption. ¨ Nonexcludable -- all consumers can consume the good. ¨ Nonrival -- one consumer’s consumption doesn’t diminish another’s.

Public Goods -- Examples Broadcast radio and TV programs. n National defense. n Public highways (nearly). n Clean air. n National parks. n A good climate. n

We will need to recall from chapter 14 that: n A consumer’s reservation price for a unit of a good is the maximum he/she is willing to pay for it. n If: ¨ Consumer’s ¨ Utility wealth is w when not having the good is U(w, 0) ¨ Utility of paying p and having one unit of the good is U(w-p, 1) n Then the reservation price r is defined by

When Should a Public Good Be Provided? One unit of the good costs c. n Two consumers, A and B. n Individual payments for providing the public good are g. A and g. B. n the good will be provided only if g. A + g. B c n

n Call the utility functions UA and UB and assume that A’s income is w. A and B’s is w. B. n Payments are individually rational if n and n which implies that g. A ≤r. A and g. B ≤ r. B

n And if and then it is Pareto-improving to supply the unit of good n (It is Pareto-improving only if one inequality holds with < and the other at least with ≤) n If c ≤ r. A + r. B it must be pareto-efficient to supply the good.

Free-riding Suppose c < r. A and 0 < r. B. n Then A would supply the good even if B made no contribution. n Then B would enjoy the good for free; be free-riding. n

Private Provision of a Public Good? n n Suppose c < r. A and c < r. B. Neither A nor B will supply the good alone. Yet, if c < r. A + r. B both could be better off if the good is supplied with a payment scheme where c < g. A + g. B ; g. A < r. A and g. B < r. B But A and B may try to free-ride on each other, causing no good to be supplied.

Free-Riding - an example n n n Suppose A and B each have just two actions - individually supply a public good, or not. Cost of supply c = 100. Payoff to A from the good = 80. Payoff to B from the good = 65. 80 + 65 > 100, so it is possible to supply the good and make both better off.

Player B Buy Don’t Buy Player A Don’t Buy (Don’t’ Buy, Don’t Buy) is the unique NE

But (Don’t buy, Don’t buy) is not efficient. n Why? n If each pays part of the cost: n For example, A contributes 60 and B contributes 40. n Payoff to A from the good = 40 > 0. n Payoff to B from the good = 25 > 0. n Any division of 100 such that g. A≤ 80 and g. B ≤ 65 will do. n

With cost-sharing there are two NE. But even if the good is supplied, there can still be some free-riding. Player B Don’t Contribute Player A Don’t Contribute

Variable Public Good Quantities E. g. how many broadcast TV programs, or how much land to include into a national park. n c(G) is the production cost of G units of public good. n Two individuals, A and B. n Private consumptions are x. A, x. B. n

n Budget allocations must satisfy MRSA & MRSB are A & B’s marg. rates of substitution between the private and public goods. n Pareto efficiency condition for public good supply is n

n n n MRSA is A’s utility-preserving compensation in private good units for a one-unit reduction in public good. Similarly for B. is ¨ the total payment to A & B of private good that preserves both utilities if G is lowered by 1 unit. ¨ the total amount of private good that A and B together are willing to give up to have G increased by 1 unit

, making 1 unit less of the public good releases more private good than the compensation payment requires Paretoimprovement from reduced G. n If the payment A and B are willing to make for 1 unit of public good provides more than 1 unit Paretoimprovement from increased G. n

n Hence, necessarily, efficient public good production requires n Suppose there are n consumers; i = 1, …, n. Then efficient public good production requires

Free-Riding Revisited When is free-riding individually rational? n Individuals can contribute only positively to public good supply; nobody can lower the supply level. n Individual utility-maximization may require a lower public good level. n Free-riding is rational in such cases. n

n Each agent decides how much to contribute based on how much everybody else is expected to contribute. ¨ For n example: Given A that contributes g. A units of public good, B’s problem is to choose x. B and g. B so as to maximise UB(x. B, g. A+ g. B) subject to x. B + g. B = w. B and g. B≥ 0
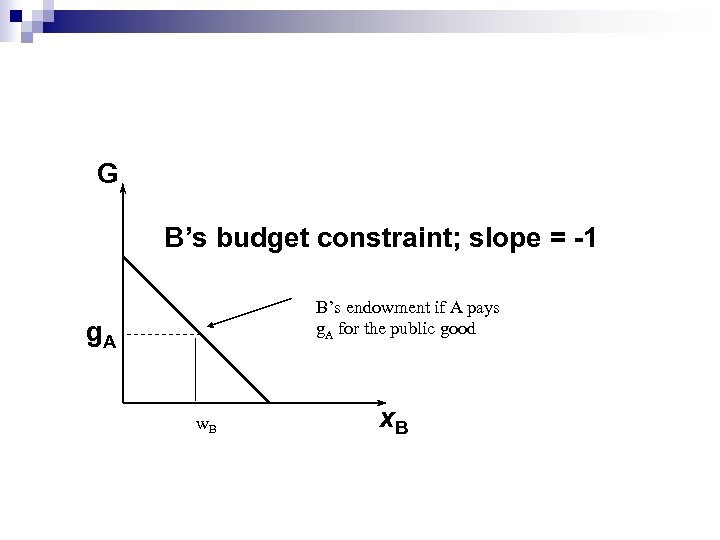
G B’s budget constraint; slope = -1 B’s endowment if A pays g. A for the public good g. A w. B x. B
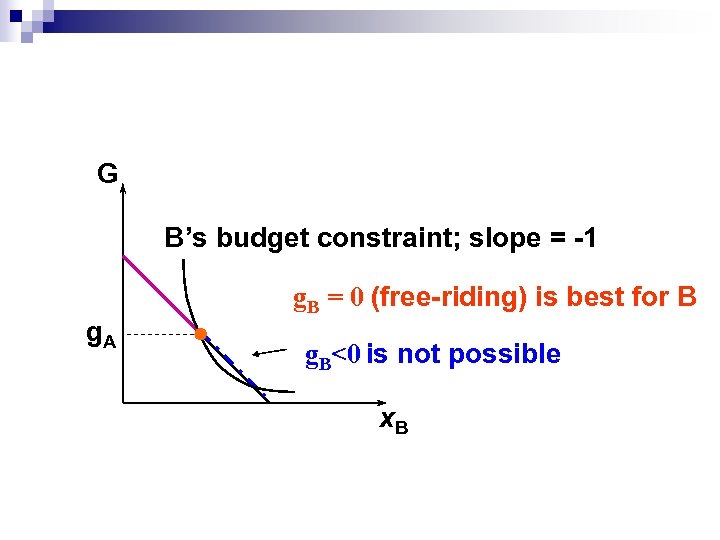
G B’s budget constraint; slope = -1 g. A g. B = 0 (free-riding) is best for B g. B<0 is not possible x. B

Demand Revelation A scheme that makes it rational for individuals to reveal truthfully their private valuations of a public good is a revelation mechanism. n For example, the Groves-Clarke taxation scheme n

Assume: n n n N individuals; i = 1, …, N. All have quasi-linear preferences. vi is individual i’s true (private) valuation of the public good. Individual i must provide ci private good units if the public good is supplied. ni = vi - ci is net value, for i = 1, …, N. Can be Pareto-improving to supply the public good if

n ni = vi - ci is net value, for i = 1, …, N. n If or and then individual j is pivotal; i. e. changes the supply decision.

n What loss does a pivotal individual j inflict on the others? n If then is the loss.

The GC tax scheme: n Assign a cost ci to each individual. n Each agent states a public good net valuation, si. n Public good is supplied if otherwise not. n

n A pivotal person j who changes the outcome from supply to not supply pays a tax of n A pivotal person j who changes the outcome from not supply to supply pays a tax of

n GC tax scheme implements efficient supply of the public good. n Note: Taxes are not paid to other individuals, but to some other agent outside the market.

An example: 3 persons; A, B and C. n Valuations of the public good are: 40 for A, 50 for B, 110 for C. n Cost of supplying the good is 180. n 180 < 40 + 50 + 110 so it is efficient to supply the good. n Assign c 1 = 60, c 2 = 60, c 3 = 60. n

B & C’s net valuations sum to (50 - 60) + (110 - 60) = 40 > 0. n A, B & C’s net valuations sum to n (40 - 60) + 40 = 20 > 0. n So A is not pivotal. n A’s true net value is 40 – 60 = -20 n If s. A > -20, then A makes supply of the public good, and a loss of 20 to him, more likely. n

n n If B and C are truthful, then what net valuation s. A should A state? If s. A > -20, then A makes supply of the public good, and a loss of 20 to him, more likely. If s. A < -20 but not enough to make A pivotal his loss is still 20. A prevents supply by becoming pivotal, only if s. A + (50 - 60) + (110 - 60) < 0; To be pivotal A must state s. A < -40.

Demand Revelation Then A suffers a GC tax of -10 + 50 = 40, n A’s net payoff is - 20 - 40 = -60 < -20. n A can do no better than state the truth; s. A = -20. n

Exercise: n Use the same method to show that n ¨B is not pivotal ¨ B can do no better than state the truth; s. B = -10. ¨ C is pivotal ¨ C can do no better than state the truth; s. C = 50.
9bed02e685048eea3bc32e374d70c53f.ppt