CHAPTER 3 Quadratic Functions and Equations Inequalities 3

CHAPTER 3: Quadratic Functions and Equations; Inequalities 3. 1 The Complex Numbers 3. 2 Quadratic Equations, Functions, Zeros, and Models 3. 3 Analyzing Graphs of Quadratic Functions 3. 4 Solving Rational Equations and Radical Equations 3. 5 Solving Equations and Inequalities with Absolute Value Copyright © 2009 Pearson Education, Inc.

3. 3 Analyzing Graphs of Quadratic Functions · · · Find the vertex, the axis of symmetry, and the maximum or minimum value of a quadratic function using the method of completing the square. Graph quadratic functions. Solve applied problems involving maximum and minimum function values. Copyright © 2009 Pearson Education, Inc.

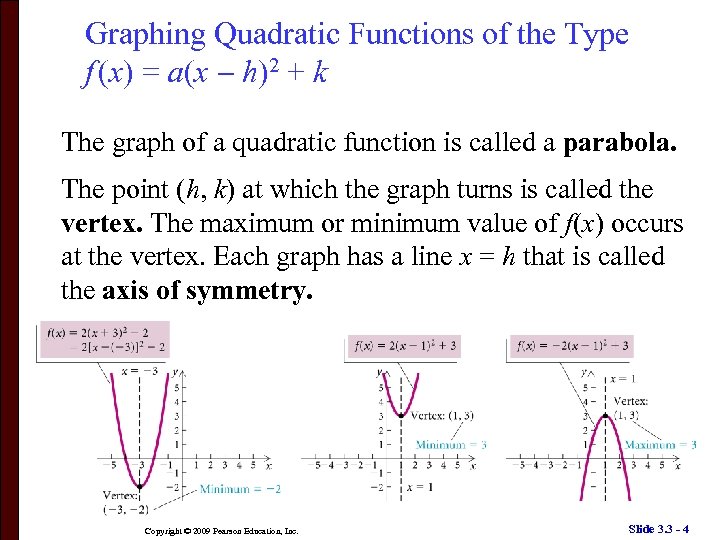Graphing Quadratic Functions of the Type f (x) = a(x h)2 + k The graph of a quadratic function is called a parabola. The point (h, k) at which the graph turns is called the vertex. The maximum or minimum value of f(x) occurs at the vertex. Each graph has a line x = h that is called the axis of symmetry. Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 4

Example Find the vertex, the axis of symmetry, and the maximum or minimum value of f (x) = x 2 + 10 x + 23. Solution: Complete the square. Vertex: (– 5, – 2) Axis of symmetry: x = – 5 Minimum value of the function: 2 Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 5

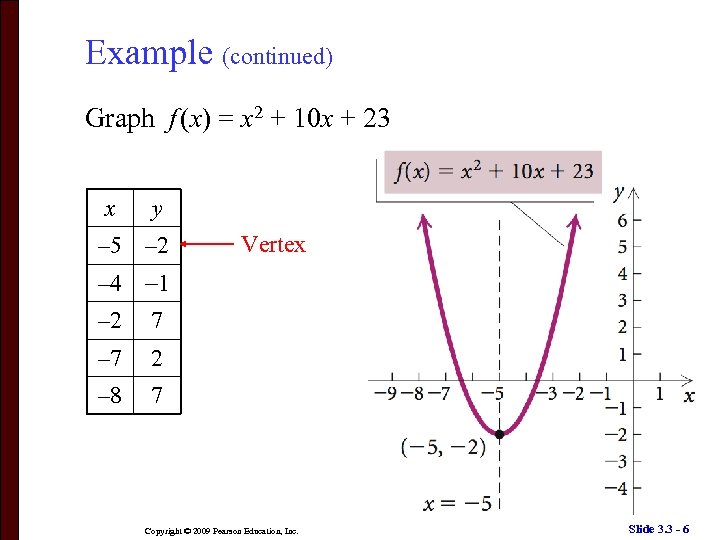Example (continued) Graph f (x) = x 2 + 10 x + 23 x y – 5 – 2 Vertex – 4 1 – 2 7 – 7 2 – 8 7 Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 6

Example Find the vertex, the axis of symmetry, and the maximum or minimum value of Solution: Complete the square. Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 7

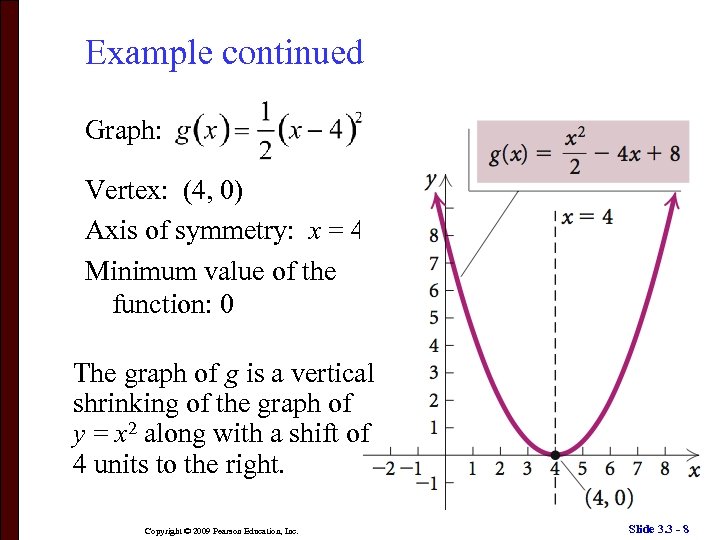Example continued Graph: Vertex: (4, 0) Axis of symmetry: x = 4 Minimum value of the function: 0 The graph of g is a vertical shrinking of the graph of y = x 2 along with a shift of 4 units to the right. Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 8

Vertex of a Parabola The vertex of the graph of f (x) = ax 2 + bx + c is We calculate the x-coordinate. Copyright © 2009 Pearson Education, Inc. We substitute to find the y-coordinate. Slide 3. 3 - 9

Example For the function f(x) = x 2 + 14 x 47: a) Find the vertex. b) Determine whethere is a maximum or minimum value and find that value. c) Find the range. d) On what intervals is the function increasing? decreasing? Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 10

Example (continued) Solution a) f (x) = x 2 + 14 x 47 The x-coordinate of the vertex is: Since f (7) = 72 + 14 • 7 47 = 2, the vertex is (7, 2). b) Since a is negative (a = – 1), the graph opens down, so the second coordinate of the vertex, 2, is the maximum value of the function. Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 11

Solution continued c) The range is ( ∞, 2]. d) Since the graph opens down, function values increase as we approach the vertex from the left and decrease as we move to the right of the vertex. Thus the function is increasing on the interval ( ∞, 7) and decreasing on (7, ∞). Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 12

Application - Example(optional) A stonemason has enough stones to enclose a rectangular patio with 60 ft of stone wall. If the house forms one side of the rectangle, what is the maximum area that the mason can enclose? What should the dimensions of the patio be in order to yield this area? Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 13

Example (continued) (optional) 1. Familiarize. Make a drawing of the situation, using w to represent the width of the fencing. 2. Translate. Since the area of a rectangle is given by length times width, we have A(w) = (60 2 w)w = 2 w 2 + 60 w. Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 14

Example (continued) (optional) 3. Carry out. We need to find the maximum value of A(w) and find the dimensions for which that maximum occurs. The maximum will occur at the vertex of the parabola, the first coordinate is Thus, if w = 15 ft, then the length l = 60 2 • 15 = 30 ft and the area is 15 • 30 = 450 ft 2. 4. Check. (15 + 30) = 60 feet of fencing. 5. State. The maximum possible area is 450 ft 2 when the patio is 15 feet wide and 30 feet long. Copyright © 2009 Pearson Education, Inc. Slide 3. 3 - 15