Chapter 3 Planning and Scheduling Planning and

Chapter 3: Planning and Scheduling

Planning and Scheduling Topics n Resolving n Bin Conflict via Coloring Packing n Scheduling Tasks n Critical-Path n Independent Schedules Tasks 2

Resolving Conflict n Goals of Three Scheduling Problems n Optimization issues – Try to maximize profit, minimize cost. n. Example: Scheduling machine time for earliest completion time 3

Resolving Conflict n Goals of Three Scheduling Problems n Equity – Try to make things fair for all participants. n. Example: Schedule baseball games (same number home and away games) 4

Resolving Conflict n Goals of Three Scheduling Problems n Conflict Resolution – Try to prevent conflicts from happening. n. Example: Scheduling college final examinations for end of term 5

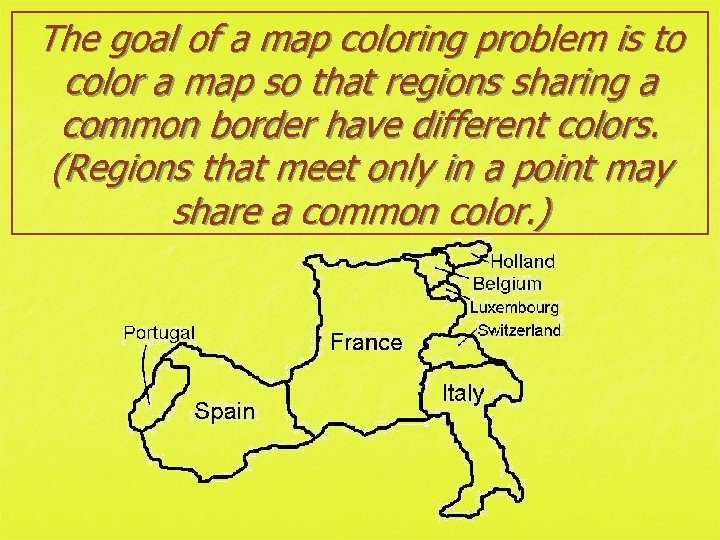The goal of a map coloring problem is to color a map so that regions sharing a common border have different colors. (Regions that meet only in a point may share a common color. )

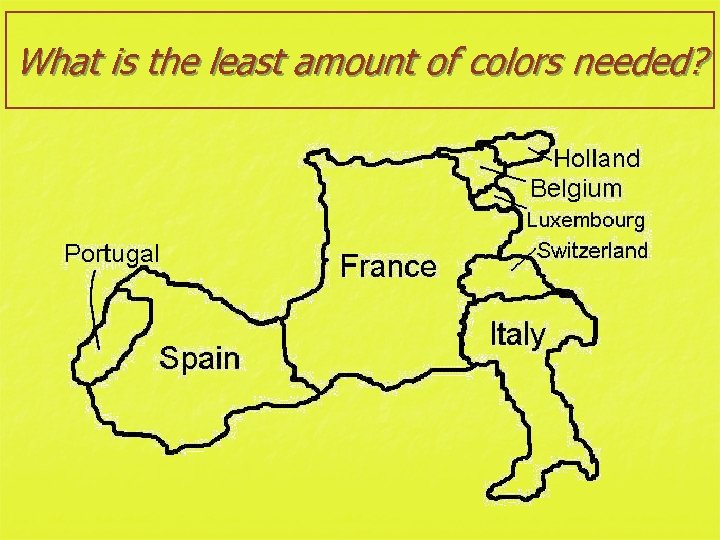What is the least amount of colors needed?

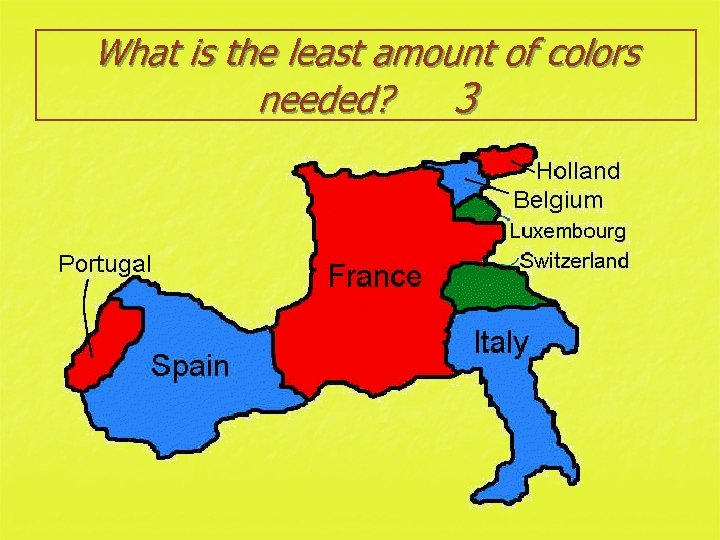What is the least amount of colors needed? 3

Resolving Conflict via Coloring n Chromatic Number The chromatic number is the minimum number of colors necessary to color a map so that regions sharing a common border have different colors

Resolving Conflict via Coloring n Chromatic Number For example, the chromatic number for the map above is 3 since it takes at least 3 colors to color the map so that regions sharing a common border have different colors. Why can't it be done with 2 colors?

Resolving Conflict via Coloring A map coloring problem can be solved by first converting the map into a graph where each region is a vertex and an edge connects two vertices if and only if the corresponding regions share a border.

Resolving Conflict via Coloring Once a map is converted into a graph, a process called vertex coloring can be used to decide how the map should be colored.

Resolving Conflict via Coloring For example, using the original graph above, we convert each country to a vertex. (We'll use open circles instead of filled dots to make it easier to color them later. )

Resolving Conflict via Coloring

Resolving Conflict via Coloring §Now we add the edges. Two countries are connected by an edge if and only if they have a common border (but not if they just meet at a point). This gives:

Resolving Conflict via Coloring

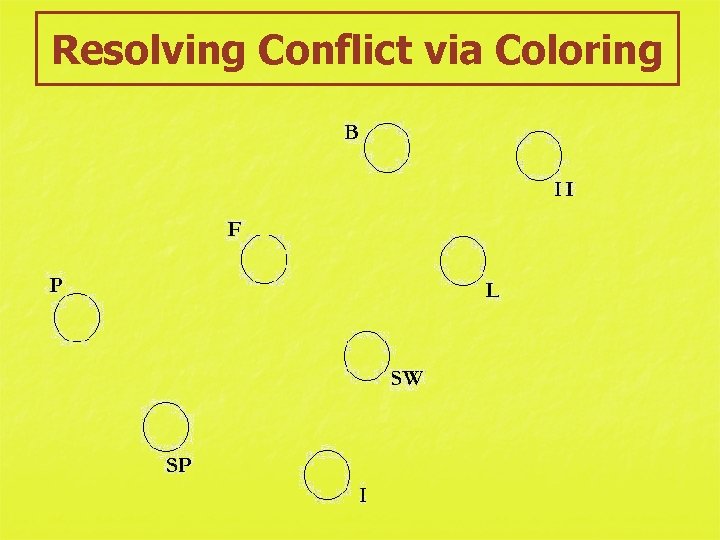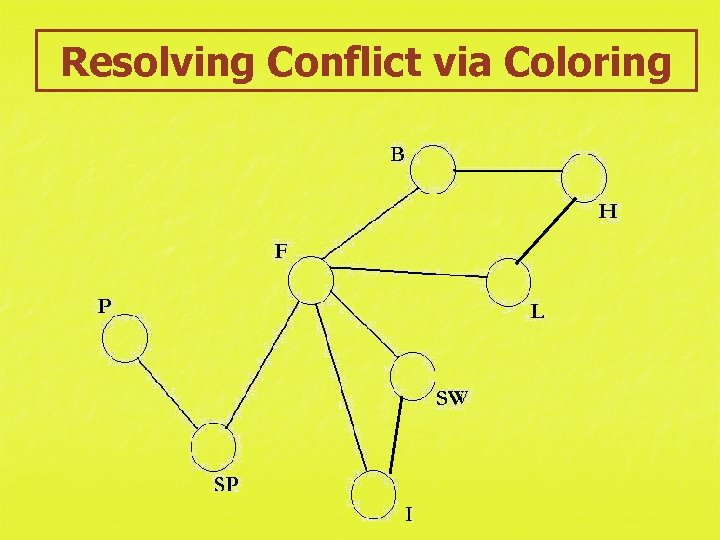
Resolving Conflict via Coloring To "color" a graph, we follow the following vertex coloring rules: Vertex coloring rules • Vertices connected by an edge must be different colors. • Use the fewest possible number of colors.

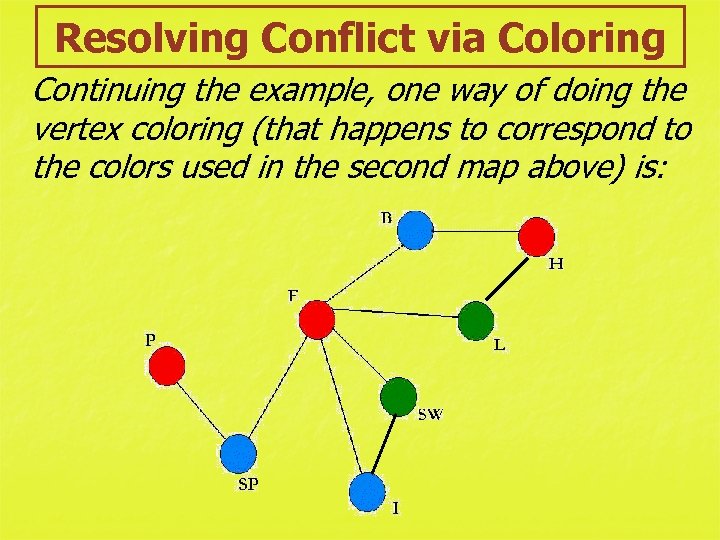Resolving Conflict via Coloring Continuing the example, one way of doing the vertex coloring (that happens to correspond to the colors used in the second map above) is:

Resolving Conflict via Coloring This same idea can be used to solve other problems. Example: n those in which people or things must be grouped or organized based on conflicts among the people or things.

Resolving Conflict via Coloring n In such a situation, the people (or things) are represented by vertices and conflicts between two people (or things) are represented by a connecting edge.

Resolving Conflict via Coloring n Example: Scheduling Exams Using Vertex Coloring n There are eight (8) finals to schedule with only two (2) airconditioned rooms. (8 courses: French-F, Math-M, History-H, Philosophy-P, English-E, Italian-I, Spanish-S, Chemistry-C). 21

Resolving Conflict via Coloring n Example: Scheduling Exams Using Vertex Coloring n In the graph, courses are represented by vertices and two course are joined by an edge for every student enrolled in both courses. 22

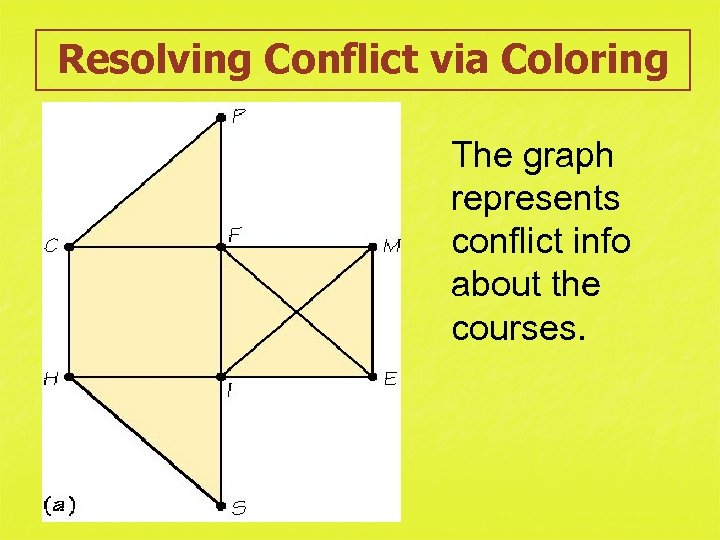Resolving Conflict via Coloring The graph represents conflict info about the courses.

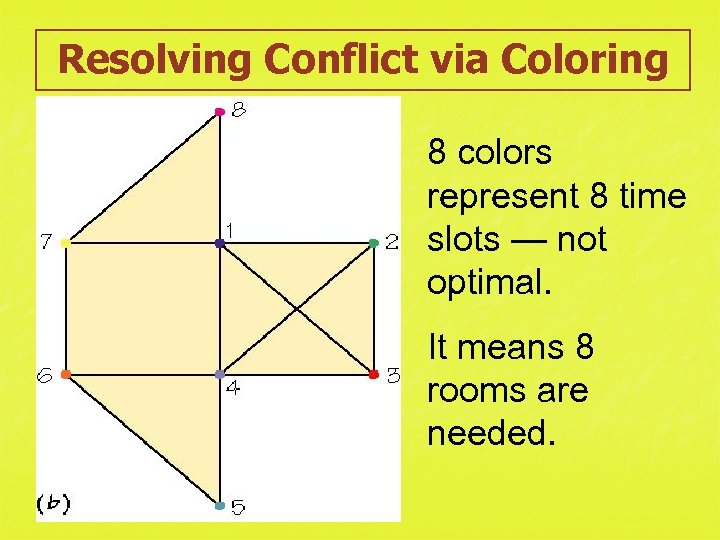Resolving Conflict via Coloring 8 colors represent 8 time slots — not optimal. It means 8 rooms are needed.

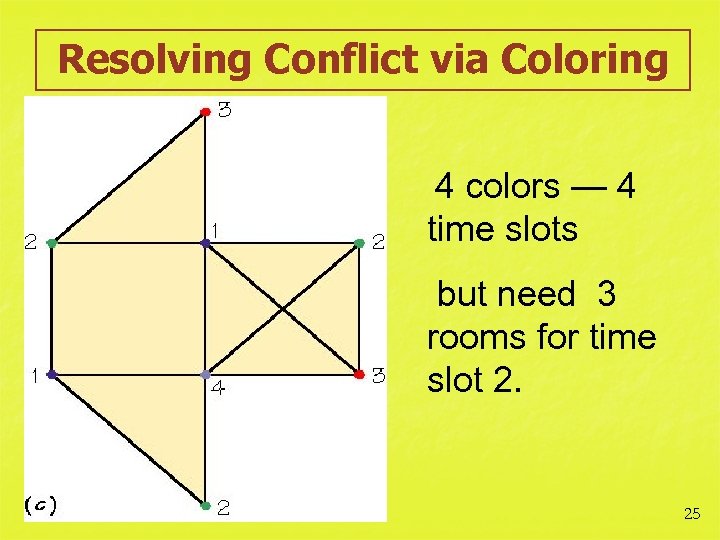Resolving Conflict via Coloring 4 colors — 4 time slots but need 3 rooms for time slot 2. 25

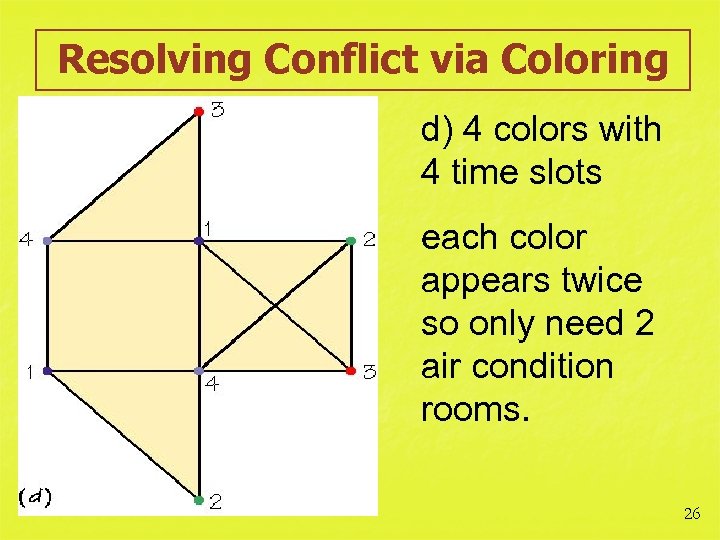Resolving Conflict via Coloring d) 4 colors with 4 time slots each color appears twice so only need 2 air condition rooms. 26

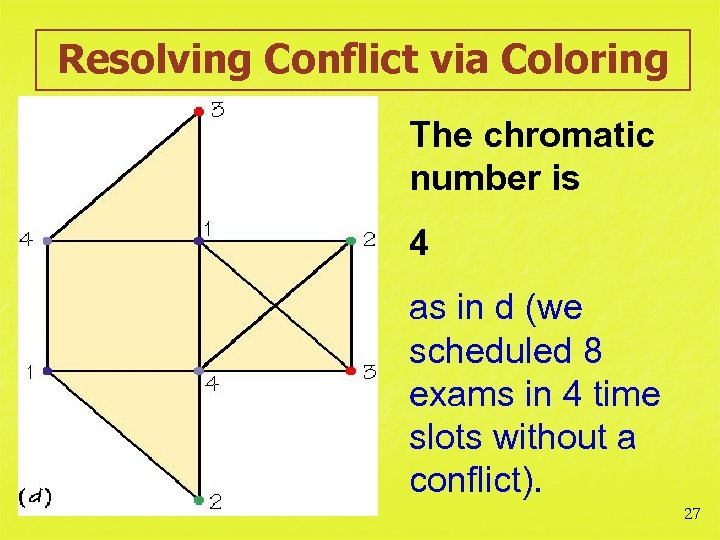Resolving Conflict via Coloring The chromatic number is 4 as in d (we scheduled 8 exams in 4 time slots without a conflict). 27

Bin Packing n The problem of finding the minimum number of bins (containers) into which the weight (object) can be packed. n Once again, there is no fast or optimal algorithm, so we will look at several methods and compare them. 28

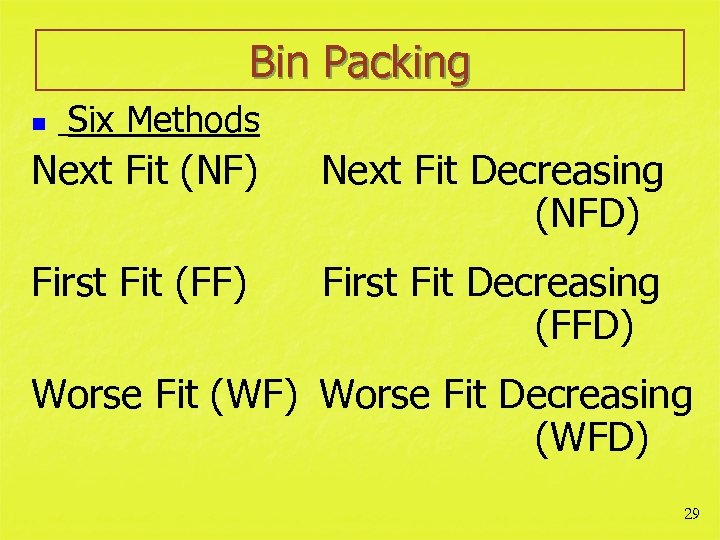Bin Packing n Six Methods Next Fit (NF) Next Fit Decreasing (NFD) First Fit (FF) First Fit Decreasing (FFD) Worse Fit (WF) Worse Fit Decreasing (WFD) 29

Bin Packing n Next Fit (NF) – A new bin is opened if the weight to be packed next will not fit in the bin that is currently being filled; the current bin is then closed. n First Fit (FF) – The next weight to be packed is placed in the lowestnumbered bin already opened into which it will fit. If it does not fit in any open bins, a new bin is opened. 30

Bin Packing n n Worse Fit (WF) – The next weight to be packed is placed into the open bin with the largest amount of room remaining. If it does not fit in any bins, open a new bin. Decreasing-Time (NFD, FFD, WFD) – list the weights in order of decreasing size before the bin-packing method. Does NOT guarantee optimal solution. 31

Bin Packing n Next Fit (NF) n Advantages – Does not require knowledge of all the weights in advance; only need to know the remaining space in the bin. n Disadvantages – The bin packed early on may have had room for small items that come later in the list. n Best method for assembly-line packing. 32

Bin Packing n First Fit (FF) n Advantages – Does not require knowledge of all the weights in advance. n Disadvantages – Large number of bins will cause issues, large amount of computer storage n Best method for small amount of items to be packed. 33

Scheduling Tasks n Examples: n. Around-the-clock scheduling of doctors and nurses, scheduling equipment (X-rays, MRI scans) for maximum efficiency n. Organizing all sub-contractors (electric, plumbing, etc) to get a house built. 34

Scheduling Tasks n Examples: n. Schedule all different crews that are necessary to prepare a plane for next flight n. Creating a High School Yearbook 35

Scheduling Tasks Accurate planning and scheduling is required of both people and machines. n. Processors q. A person, machine, robot, operating room, or runway (for airplanes) whose time must be scheduled. 36

Scheduling Tasks Accurate planning and scheduling is required of both people and machines. n. Machine-Scheduling Problem q. The problem of deciding how the tasks should be scheduled so the entire job is completed as early as possible. 37

Scheduling Tasks n Assumptions n When a processor starts a task, it will be completed without interruption. n Any processor can work on any of the tasks. n No processor stays idle voluntarily. 38

Scheduling Tasks n Assumptions n Order-requirement digraph is used to show the task order and has the task times highlighted within each vertex. n Priority lists arrange the tasks in order, independent of the order requirements. Used to “break ties” if more than one task is ready. 39

Scheduling Tasks n Goals to Consider n Minimize job. the completion time of the n Minimize the total time the processors are idle. n Find the minimum number of processors necessary to finish the job by a specified time. 40

When is the schedule optimal? n Optimal Time = Total time of all tasks/# processors. n Completion processor n Idle Time: length of longest Time is the amount of total time the processors are not used. 41

When is the schedule optimal? If the schedule completion time = the length of critical path, then the schedule is optimal (earliest completion time). 42

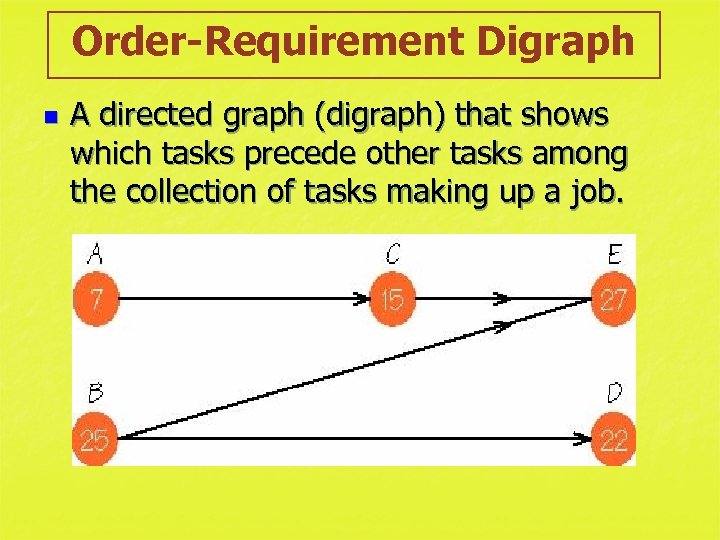Order-Requirement Digraph n A directed graph (digraph) that shows which tasks precede other tasks among the collection of tasks making up a job.

Independent Tasks n Tasks that are independent of each other if they can be performed in any order (no edges in the order-requirement digraph). n Label the tasks by their task times rather than their task number.

Independent Tasks n The list-processing algorithm can be used to schedule the tasks onto machines using the given list but may not be efficient. n Geometrically, we can think of independent tasks as rectangles of height 1.

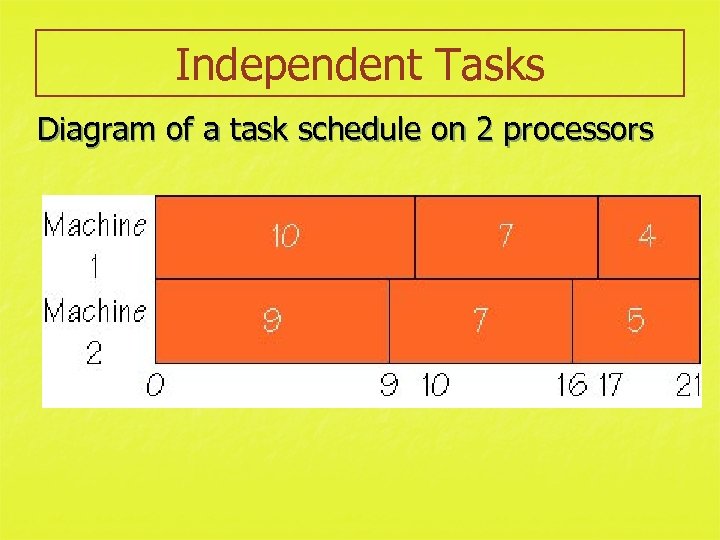Independent Tasks Diagram of a task schedule on 2 processors

List Processing Algorithm Also called “First come, First serve” Algorithm 1. Put finger on available processor (whenever there is a tie, lowest numbered processor). 2. Schedule 1 st task from the priority list on the available processor. Cross it off the list. 47

List Processing Algorithm 3. Put finger on processor that is behind. Schedule next task from the priority list onto the processor. Remove this task from priority list. 4. Repeat 1 -3 until all tasks are scheduled. 5. Create idle time to “even-up” processors. 48

Decreasing-Time List Algorithm 1) Arrange tasks in decreasing order by time. This becomes the priority list, 2) Apply the List Processing Algorithm.

Decreasing-Time List Algorithm Example: Apply decreasing-time list algorithm on independent tasks 10, 9, 7, 7, 5, 4 (already in order) This result is an optimal schedule!

Dependent Tasks Complications arise with jobs consisting of several tasks that cannot be done in an arbitrary order.

Dependent Tasks Example: Treating the job of building a house as a scheduling problem, what must occur first? Order these tasks: working on the roof, putting up the walls, laying the foundation Laying foundation, putting up the walls, working on roof

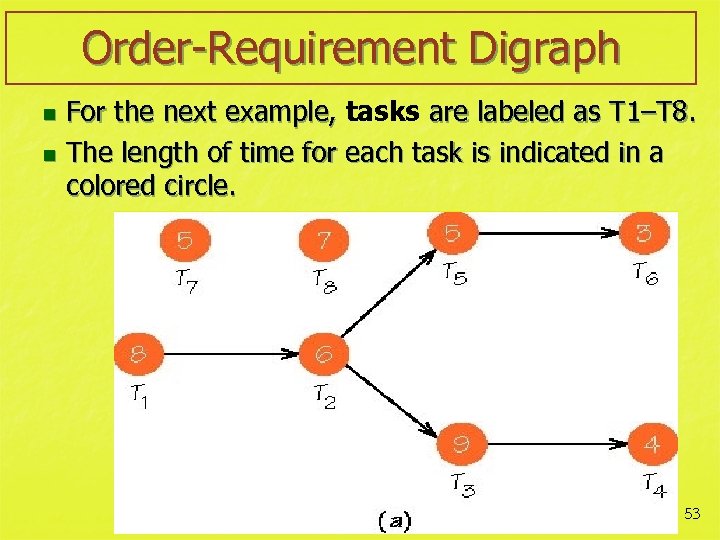Order-Requirement Digraph For the next example, tasks are labeled as T 1–T 8. n The length of time for each task is indicated in a colored circle. n 53

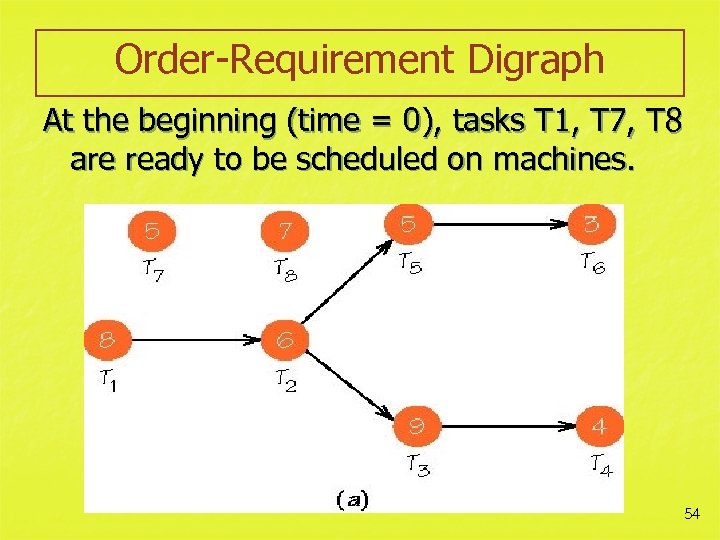Order-Requirement Digraph At the beginning (time = 0), tasks T 1, T 7, T 8 are ready to be scheduled on machines. 54

Scheduling Tasks n. Processors q. For this example, tasks will be scheduled on two machines according to the order-requirement digraph and priority list. 55

Scheduling Tasks Priority List q A list that ranks the tasks in some criterion of importance. Used to “break ties” if more than one task is ready. 56

Scheduling Tasks Priority List q. Ready task – A task is ready if its predecessors have been completed by that time as given by the orderrequirement digraph. q. For the problem, the priority list is T 1, T 2, T 3, T 4, T 5, T 6, T 7, T 8. 57

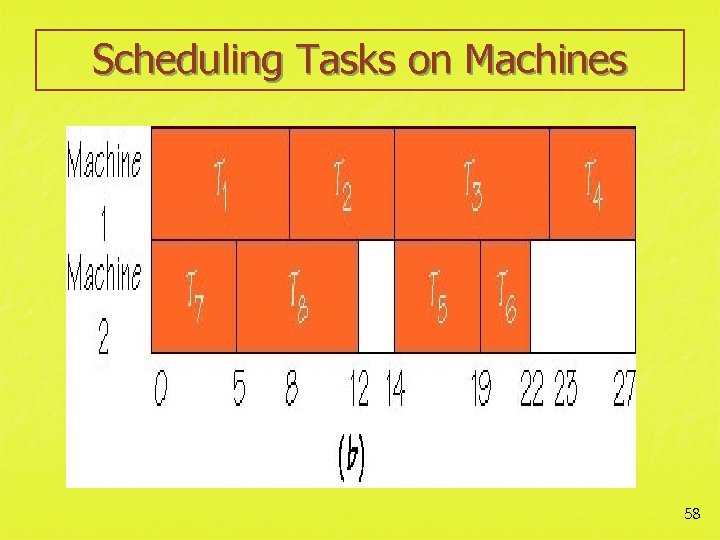Scheduling Tasks on Machines 58

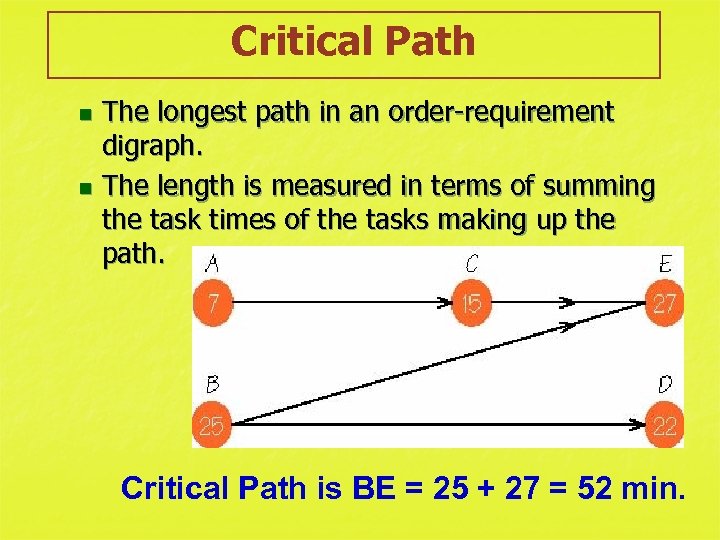Critical Path The longest path in an order-requirement digraph. n The length is measured in terms of summing the task times of the tasks making up the path. n Critical Path is BE = 25 + 27 = 52 min.

Critical Path Schedules A systematic method of choosing/creating a priority list, that yields optimal, or nearly optimal, schedules. 60

Critical Path Scheduling Algorithm (to create a Priority List) 1. 2. Evaluate paths and find critical (longest) path in the orderrequirement digraph. If a tie, choose path with the lowest-number task. Remove first task occurring in that path and put it first in the priority list. (Remove the task found in step 1 and the edges attached to it from the current order-requirement digraph). 61

Critical Path Scheduling Algorithm (to create a Priority List) 3. With this task removed, evaluate new completion time for this path. (reduce path by length of task). 4. If there is more than one path from which to choose, assign the lowest numbered task to the priority list. 62

Critical Path Scheduling Algorithm (to create a Priority List) 5. Repeat 1 -4 until all tasks have been placed on the priority list. 6. Apply list processing algorithm, along with order-requirement digraph, to schedule all tasks on the given number of processors. 63

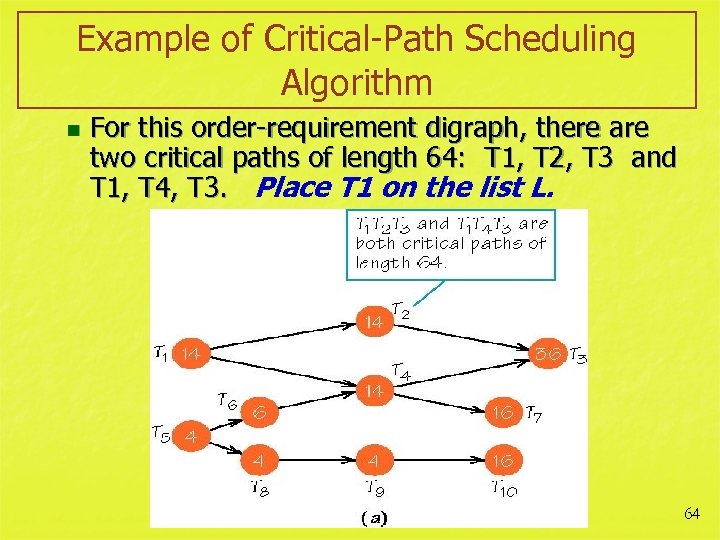Example of Critical-Path Scheduling Algorithm n For this order-requirement digraph, there are two critical paths of length 64: T 1, T 2, T 3 and T 1, T 4, T 3. Place T 1 on the list L. 64

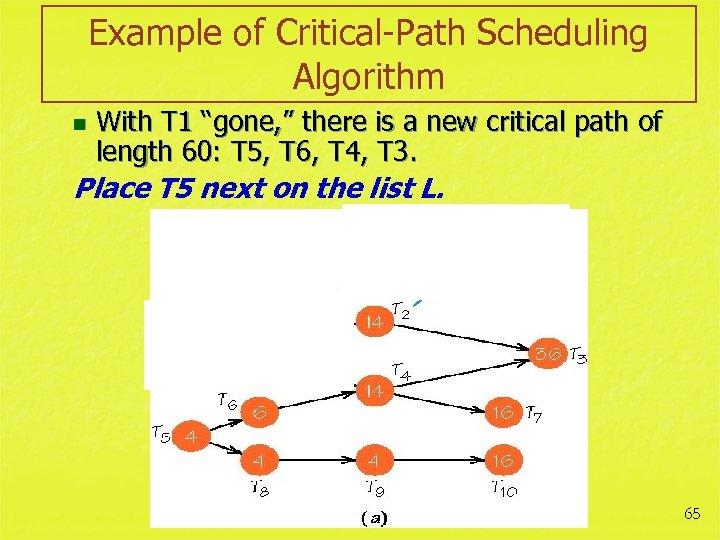Example of Critical-Path Scheduling Algorithm n With T 1 “gone, ” there is a new critical path of length 60: T 5, T 6, T 4, T 3. Place T 5 next on the list L. 65

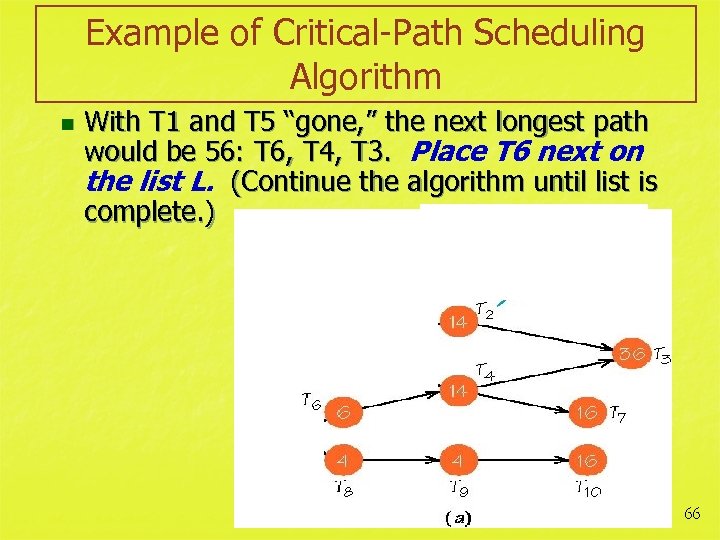Example of Critical-Path Scheduling Algorithm n With T 1 and T 5 “gone, ” the next longest path would be 56: T 6, T 4, T 3. Place T 6 next on the list L. (Continue the algorithm until list is complete. ) 66

Critical Path Schedules n The new priority list would be: T 1, T 5, T 6, T 2, T 3, T 8, T 9, T 7, T 10. Using the list-processing algorithm with the new priority list, the following schedule is obtained: 67

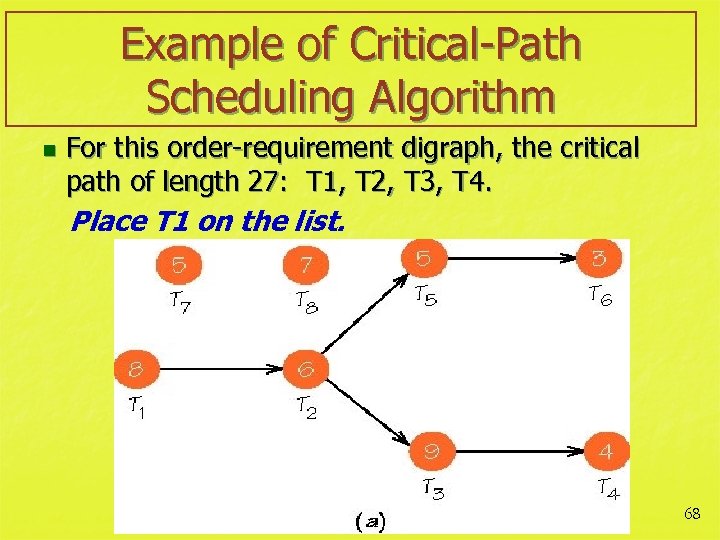Example of Critical-Path Scheduling Algorithm n For this order-requirement digraph, the critical path of length 27: T 1, T 2, T 3, T 4. Place T 1 on the list. 68