CHAPTER 3 Linear Equations and Functions SECTION

CHAPTER 3 Linear Equations and Functions

SECTION 3 -1 Open Sentences in Two Variables

DEFINITIONS Open sentences in two variables– equations and inequalities containing two variables

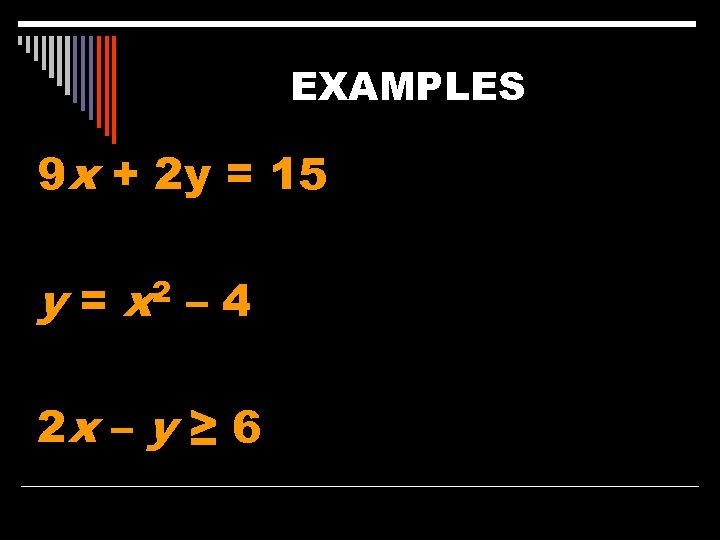EXAMPLES 9 x + 2 y = 15 y = x 2 – 4 2 x – y ≥ 6

DEFINITIONS Solution– is a pair of numbers (x, y) called an ordered pair.

DEFINITIONS Solution set– is the set of all solutions satisfying the sentence. Finding the solution is called solving the open sentence.

EXAMPLE Solve the equation: 9 x + 2 y = 15 if the domain of x is {-1, 0, 1, 2}

SOLUTION x -1 0 1 (15 -9 x)/2 [15 -9(-1)]/2 [15 -9(0)]/2 [15 -9(1)]/2 y 12 15/2 3 Solution (-1, 12) (0, 15/2) (1, 3) 2 [15 -9(2)]/2 -3/2 (2, -3/2)

SOLUTION the solution set is {(-1, 12), (0, 15/2), (1, 3), (2, 3/2)}

EXAMPLE Roberto has $22. He buys some notebooks costing $2 each and some binders costing $5 each. If Roberto spends all $22 how many of each does he buy?

SOLUTION n = number of notebooks b = number of binders (n and b must be whole numbers) 2 n + 5 b =22 n = (22 -5 b)/2

SOLUTION If n is odd then 22 -5 b is odd and n is not a whole number

SOLUTION b 0 2 4 (22 -5 b)/2 [22 -5(0)]/2 [22 -5(2)]/2 [22 -5(4)]/2 n 11 6 1 Solution (0, 11) (2, 6) (4, 1) 6 [12 -5(6)]/2 -4 Impossible

SOLUTION the solution set is {(0, 11), (2, 6), (4, 1)}

SECTION 3 -2 Graphs of Linear Equations in Two Variables

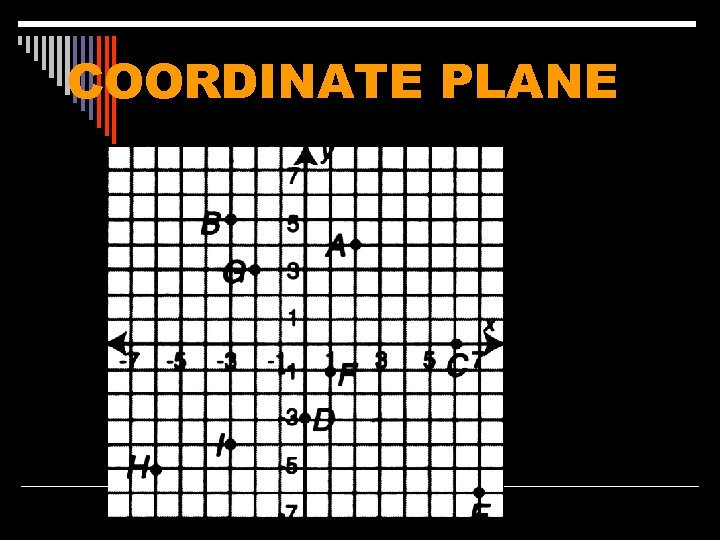
COORDINATE PLANE consists of two perpendicular number lines, dividing the plane into four regions called quadrants

COORDINATE PLANE

X-coordinate (abscissa)- the horizontal number line Y-coordinate (ordinate) - the vertical number line ORIGIN - the point where the x-coordinate and y-coordinate cross

DEFINITION ORDERED PAIR - a unique assignment of real numbers to a point in the coordinate plane consisting of one x-coordinate and one y-coordinate (-3, 5), (2, 4), (6, 0), (0, -3)

ONE-TO-ONE CORRESPONDENCE 1. There is exactly one point in the coordinate plane associated with each ordered pair of real numbers.

ONE-TO-ONE CORRESPONDENCE 2. There is exactly one ordered pair of real numbers associated with each point in the coordinate plane.

DEFINITION GRAPH – is the set of all points in the coordinate plane whose coordinates satisfy the open sentence.

THEOREM The graph of every equation of the form Ax + By = C (A and B not both zero) is a line. Conversely, every line in the coordinate plane is the graph of an equation of this form

LINEAR EQUATION is an equation whose graph is a straight line.

SECTION 3 -3 The Slope of a Line

SLOPE is the ratio of vertical change to the horizontal change. The variable m is used to represent slope.

FORMULA FOR SLOPE m = change in y-coordinate change in x-coordinate m = rise run Or

SLOPE OF A LINE m = y 2 – y 1 x 2 – x 1

HORIZONTAL LINE a horizontal line containing the point (a, b) is described by the equation y = b and has slope of 0

VERTICAL LINE a vertical line containing the point (c, d) is described by the equation x = c and has no slope

Find the slope of the line that contains the given points. M(4, -6) and N(-2, 3) m = 3 –(-6) -2 – 4 m=3+6 -6 m = - 9/6 or -3/2

THEOREM The slope of the line Ax + By = C (B ≠ 0) is - A/B

THEOREM Let P(x 1, y 1) be a point and m a real number. There is one and only one line L through P having slope m. An equation of L is y – y 1 = m (x – x 1)

Write an equation of a line with the given slope and through a given point m=-2 P(-1, 3) y-3=-2[x-(-1)] y-3= -2(x+1) y-3= -2 x-2 y=-2 x+1

SECTION 3 -4 Finding an Equation of a Line

POINT-SLOPE FORM y – y 1 = m (x – x 1) where m is the slope and (x 1 , y 1) is a point on the line.

Write an equation of a line with the given slope and passing through a given point m=-2 P(-1, 3) y-3=-2[x-(-1)] y-3= -2(x+1) y-3= -2 x-2 y=-2 x+1

Y-Intercept is the point where the line intersects the y axis.

X-Intercept is the point where the line intersects the x -axis.

SLOPE-INTERCEPT FORM y = mx + b where m is the slope and b is the y -intercept

Write an equation of a line with the given y-intercept and slope m=3 b = 6 y=3 x + 6

THEOREM Let L 1 and L 2 be two different lines, with slopes m 1 and m 2 respectively. 1. L 1 and L 2 are parallel if and only if m 1=m 2

THEOREM and 2. L 1 and L 2 are perpendicular if and only if m 1 m 2 = -1

Write an equation of a line passing through the given points A(1, -3) B(3, 2) y-(-3)=[2 -(-3)](x-1) 3 -1 y+3=5(x-1) 2 y+3=5 x-5 2 2 y=5 x-11 2 2

Find the slope of a line parallel to the line containing points M and N. M(-2, 5) and N(0, -1) m = -1 -5 0 – (-2) m = -6 2 m=-3

Find the slope of a line perpendicular to the line containing points M and N. M(4, -1) and N(-5, -2) m = -2 – (-1) -5 - 4 m = -1 -9 m = 1/9

Write an equation of a line parallel to y=-1/3 x+ containing the point (1, 1) m=-1/3 P(1, 1) y-1=-1/3(x-1) y-1= -1/3 x+1/3 y= -1/3 x+4/3

Write an equation of a line perpendicular to y= 1/3 x+1 containing the point (1, 1) m=-1/3 P(1, 1) y-1=-1/3(x-1) y-1= -1/3 x+1/3 y= -1/3 x+4/3

SECTION 3 -5 Systems of Linear Equations in Two Variables

SYSTEM OF EQUATIONS Two linear equations with the same two variable form a system of equations.

SOLUTION The ordered pair that makes both equations true.

INTERSECTING LINES The SOLUTION to the system of equations is a point (point of intersection of the two lines).

PARALLEL LINES There is NO SOLUTION to the system of equations (no intersection of the two lines).

COINCIDING LINES The graph of each equation is the same. The lines coincide and any point on the line is a solution.

EQUIVALENT SYSTEMS Systems that have the same solution.

METHODS FOR SOLVING SYSTEM OF EQUATIONS o. Graphing o. Substitution o. Linear- Combination

SOLVE BY GRAPHING 4 x + 2 y = 8 3 y = -6 x + 12

SOLVE BY GRAPHING y = 1/2 x + 3 2 y = x - 2

SUBSTITUTION A method for solving a system of equations by solving for one variable in terms of the other variable.

SOLVE BY SUBSTITUTION 3 x – y = 6 x + 2 y = 2 Solve for y in terms of x. 3 x – y = 6 3 x = 6 + y 3 x – 6 = y then

SOLVE BY SUBSTITUTION Substitute the value of y into the second equation x + 2 y = 2 x + 2(3 x – 6) = 2 x + 6 x – 12 = 2 7 x = 14 x = 2 now

SOLVE BY SUBSTITUTION Substitute the value of x into the first equation 3 x – y = 6 y = 3 x – 6 y = 3(2 – 6) y = 3(-4) y = -12

SOLVE BY SUBSTITUTION 2 x + y = 0 x – 5 y = -11 Solve for y in terms of x. 2 x + y = 0 y = -2 x then

SOLVE BY SUBSTITUTION Substitute the value of y into the second equation x – 5 y = -11 x – 5(-2 x) = -11 x+ 10 x = -11 11 x = -11 x = -1

SOLVE BY SUBSTITUTION Substitute the value of x into the first equation 2 x + y = 0 y = -2 x y = -2(-1) y=2

LINEAR-COMBINATION Another method for solving a system of equations where one of the variables is eliminated by adding or subtracting the two equations.

LINEAR COMBINATION v. If the coefficients of one of the variables are opposites, add the equations to eliminate one of the variables. If the coefficients of one of the variables are the same, subtract the equations to eliminate one of the variables.

LINEAR COMBINATION v. Solve the resulting equation for the remaining variable.

LINEAR COMBINATION v. Substitute the value for the variable in one of the original equations and solve for the unknown variable.

LINEAR COMBINATION v. Check the solution in both of the original equations.

LINEAR COMBINATION v. This method combines the multiplication property of equations with the addition/subtraction method.

SOLVE BY LINEARCOMBINATION 3 x – 4 y = 10 3 y = 2 x – 7

SOLUTION 3 x – 4 y = 10 -2 x +3 y = -7 Multiply equation 1 by 2 Multiply equation 2 by 3

SOLUTION 6 x – 8 y = 20 -6 x +9 y = -21 Add the two equations. y = -1

SOLUTION Substitute the value of y into either equation and solve for 3 x – 4 y = 10 3 x – 4(-1) = 10 3 x + 4 = 10 3 x = 6 x=2

CONSISTENT SYSTEM The system of equations has at least one solution.

INCONSISTENT SYSTEM The system of equations has no solution.

DEPENDENT SYSTEM The graph of each equation is the same. The lines coincide and any point on the line is a solution.

SECTION 3 -6 Problem Solving: Using Systems

EXAMPLE If 8 pens and 7 pencils cost $3. 37 while 5 pens and 11 pencils cost $3. 10, how much does each pen and each pencil cost?

SOLUTION Let x = cost of a pen y = cost of a pencil 8 x + 11 y = 3. 37 5 x + 11 y = 3. 10

SOLUTION Solve the system of equations. x = 29 y = 15

EXAMPLE To use a certain computer data base, the charge is $30/hr during the day and $10. 50/hr at night. If a research company paid $411 for 28 hr of use, find the number of hours charged at the daytime rate and at the nighttime rate.

SOLUTION Let x = number of hrs at daytime rate y = number of hrs at nighttime rate 30 x + 10. 50 y = 411 x + y = 28

SOLUTION Solve the system of equations. x=6 y = 22

SECTION 3 -7 Linear Inequalities in Two Variables

SYSTEM OF INEQUALITIES Linear equations that have the equal sign replaced by one of these symbols <, ≤, ≥, >

SYSTEM OF LINEAR INEQUALITIES The SOLUTION of an inequality in two variables is an ordered pair of numbers that satisfies the inequality.

SYSTEM OF LINEAR INEQUALITIES A system of linear inequalities can be solved by graphing each associated equation and determining the region where the inequality is true.

HALF-PLANE Graphically its the region on either side of the line.

BOUNDARY is the line separating the half-planes

OPEN HALF-PLANE is the region on either side of the boundary line (illustrated by a dashed-line).

CLOSED HALF-PLANE is the solution that includes the boundary line.

GRAPH of an INEQUALITY is a graph of all the solutions of the inequality and includes a boundary, either a solid line or dashed line and a shaded area.

TEST POINT is a point that does not lie on the boundary, but rather above or below it.

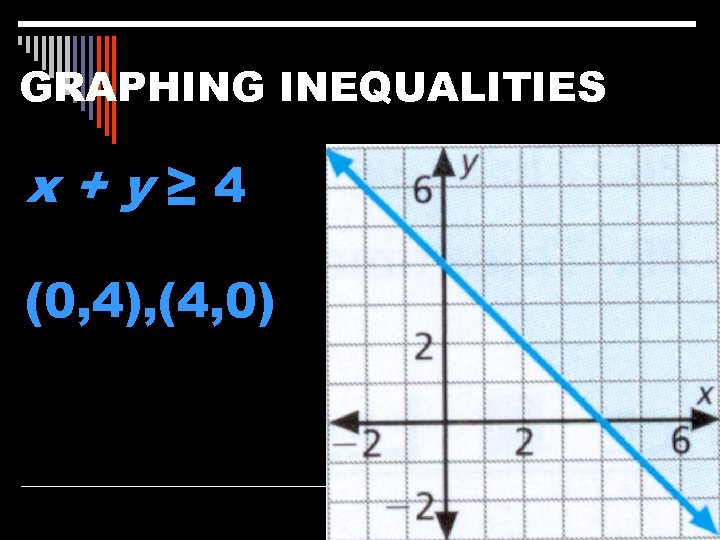GRAPHING INEQUALITIES x+y≥ 4 (0, 4), (4, 0)

Shade the region above a dashed line if y > mx + b.

Shade the region above a solid line if y mx + b.

Shade the region below a dashed line if y < mx + b.

Shade the region below a solid line if y ≤ mx + b.

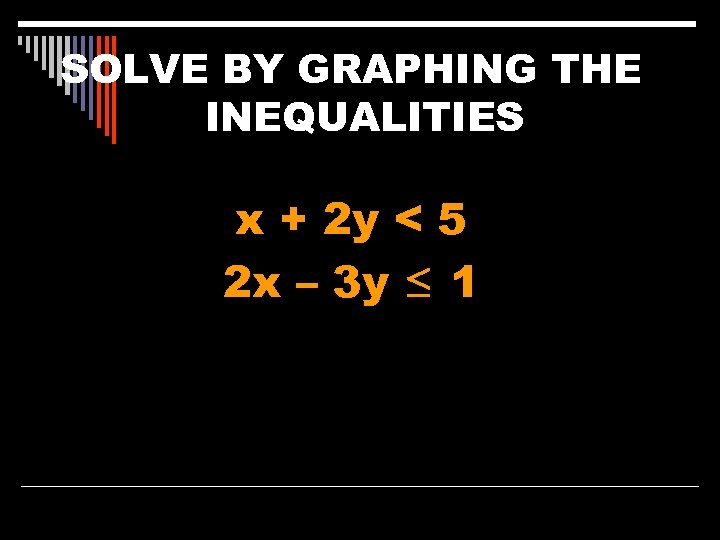SOLVE BY GRAPHING THE INEQUALITIES x + 2 y < 5 2 x – 3 y ≤ 1

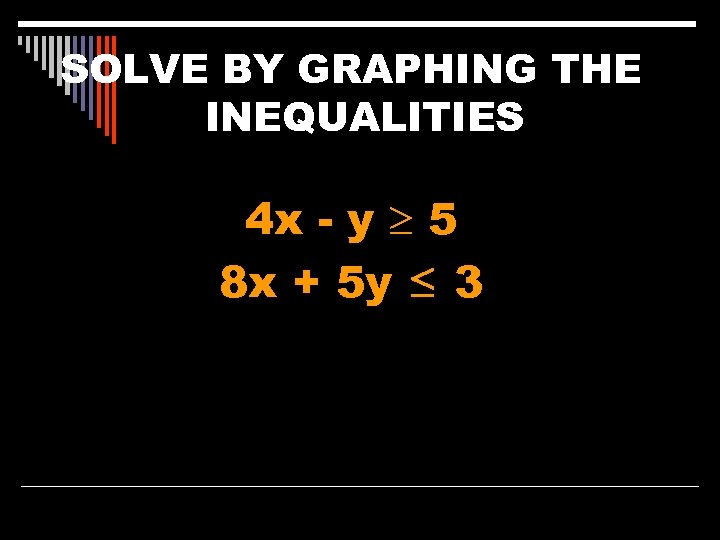SOLVE BY GRAPHING THE INEQUALITIES 4 x - y 5 8 x + 5 y ≤ 3

SECTION 3 -8 Functions

MAPPING DIAGRAM A picture showing a correspondence between two sets

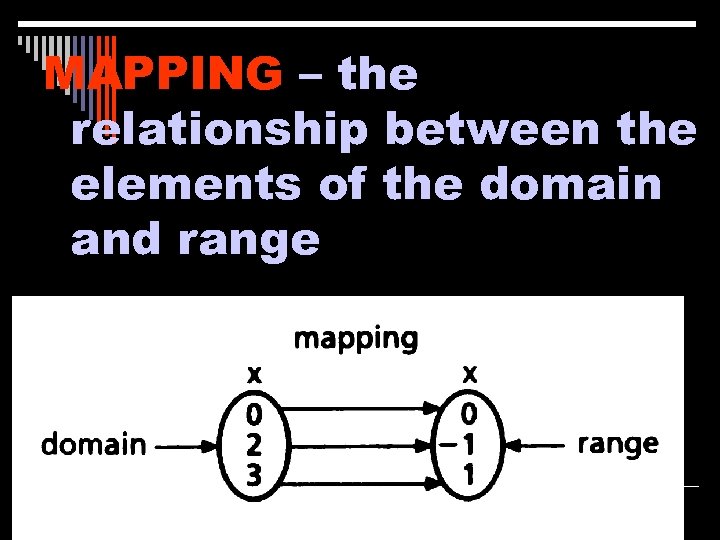MAPPING – the relationship between the elements of the domain and range

DOMAIN – the set of all possible x-coordinates RANGE – the set of all possible y-coordinates

FUNCTION A correspondence between two sets, D and R, that assigns to each member of D exactly one member of R.

Introduction to Functions Definition – A function f from a set D to a set R is a relation that assigns to each element x in the set D exactly one element y in the set R. The set D is the domain of the function f, and the set R contains the range

Characteristics of a Function 1. Each element in D must be matched with an element in R. 2. Some elements in R may not be matched with any element in D. 3. Two or more elements in D may be matched with the same element in R. 4. An element in D (domain) cannot be match with two different elements in R.

Example A = {1, 2, 3, 4, 5, 6} and B = {9, 10, 12, 13, 15} Is the set of ordered pairs a function? {(1, 9), (2, 13), (3, 15), (4, 15), (5, 12), (6, 10)}

EXAMPLE Given f: x→ 4 x – x 2 with domain D= {1, 2, 3, 4, 5} Find the range of f. f, the function that assigns to x the number 4 x – x 2

SOLUTION x 1 2 3 4 5 4 x -x 2 4(1) – 4(2) – 4(3) – 4(4) – 4(5) – 1=3 4=4 9=3 16 = 0 25 = -5 (x, y) (1, 3) (2, 4) (3, 3) (4, 0) (5, -5)

FUNCTIONAL NOTATION f(x) denotes the value of f at x

VALUES of a FUNCTION The members of its range.

SECTION 3 -9 Linear Functions

Linear Function Is a function f that can be defined by f(x) = mx + b Where x, m and b are real numbers. The graph of f is the graph of y = mx +b, a line with slope m and y intercept b.

Constant Function If f(x) = mx + b and m = 0, then f(x) = b for all x and its graph is a horizontal line y = b

Rate of Change m = change in f(x) Change in x

EXAMPLE Find equations of the linear function f using the given information. f(4) = 1 and f(8) = 7

SOLUTION m = f(8) – f(4) 8– 4 m = 3/2

SECTION 3 -10 Relations

RELATION Is any set of ordered pairs. The set of first coordinates in the ordered pairs is the domain of the relation, and

RELATION and the set of second coordinates is the range.

FUNCTION is a relation in which different ordered pairs have different first coordinates.

VERTICAL LINE TEST a relation is a function if and only if no vertical line intersects its graph more than once.

Determine if Relation is a Function {2, 1), (1, -2), (1, 2)} {(x, y): x + y = 3}

END