Chapter 3 EDRS 5305 Fall 2005 Gravetter and

Chapter 3 EDRS 5305 Fall 2005 Gravetter and Wallnau 5 th edition

Central Tendency (defined) ► Definition § A statistical measure to determine a single score that defines the center of a distribution. ► Goal § To find the single score that is most typical or most representative of the entire group (i. e. average).

Central Tendency (cont. ) ► Data is easier to understand; ► Problem § No single standard procedure for determining central tendency. § No single measure will always produce a central, representative value in every situation.

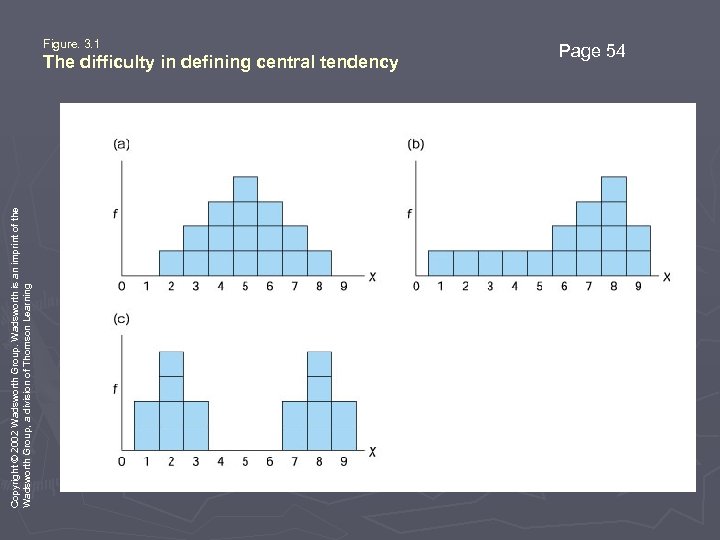Copyright © 2002 Wadsworth Group. Wadsworth is an imprint of the Wadsworth Group, a division of Thomson Learning Figure. 3. 1 The difficulty in defining central tendency Page 54

Mean, Median, Mode ► To deal with the problems, statisticians have developed three different methods for measuring central tendency. ► How do you decide which one to use? § Keep in mind – the general purpose of central tendency is to find the single most representative score.

Mean ► Arithmetic average ► Add all the scores and divide by the number of scores. ► For the average of a population use the Greek letter mu, m (myoo) ► For the mean for a sample use X (read as X-bar) or M

Mean ► The mean for a distribution is the sum of the scores divided by the number of scores. ► Formula m = SC N Population Mean M=SC n Sample Mean

Why Greek letters? ► Greek ► Our letters to identify population values own alphabet to identify sample values M Sample n n is used for the number of scores in the sample

Example For a population N=4 scores: 3, 7, 4, 6 m = S C = 20 = 5 N 4 Page 55

Alternative Definitions for Mean ► The mean can be thought of as an amount each individual would get if the total (S C) were equally divided among all the individuals (N) in the distribution. ► Example 3. 2 pg. 55 n=6 boys Buy 180 baseball cards Each gets 30 cards n = 4 boys M = $5 $20 total Do not know how much each boy has

Alternative Definitions for Mean ► Define the mean as a balance point for the distribution. ► Example 3. 2 pg. 56

Weighted Mean ► Combining two sets of scores and then finding the overall mean for the combined group. ► Example pg. 57 ► Because the samples are not the same size, one will make a larger contribution to the total group and therefore will carry more weight in determining the overall mean. ► The overall mean is called the weighted mean.

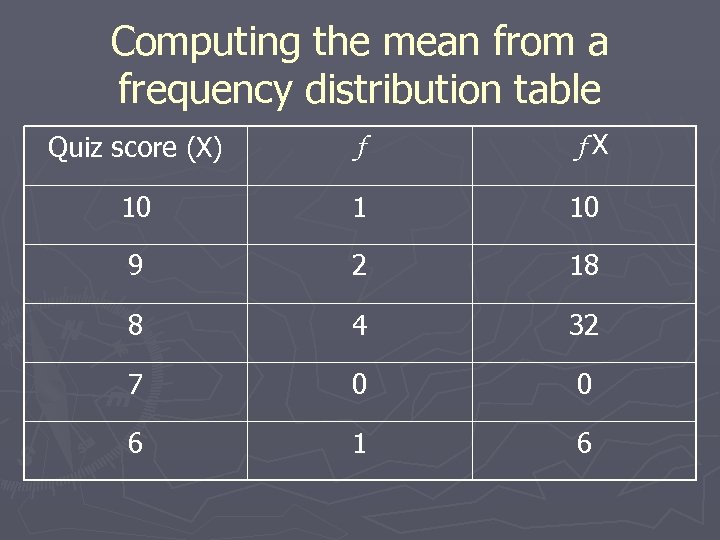Computing the mean from a frequency distribution table Quiz score (X) f f. X 10 1 10 9 2 18 8 4 32 7 0 0 6 1 6

Characteristics of the Mean ► Every score in the distribution contributes to the value of the mean. § Every score must be added into the total in order to compute the mean. ► Changing the value of the score will change the mean ► Introducing a new score or removing a score will change the value of the mean

Median ► The score that divides a distribution exactly in half. ► No symbols or notations ► Definition and computations are identical for a sample and for a population ► Goal of a median is to determine the precise midpoint of a distribution.

Example ► When N is an odd number 3, 5, 8, 10, 11 ► When N is an even number 3, 3, 4, 5, 7, 8 Median = 4. 5

Median (cont. ) ► Used when a researcher wants to divide the sample or population into two groups that are exactly the same size. ► Median split § Where one group is above the median line and the other is below § For example: one of high-scoring subjects and one of low-scoring subjects

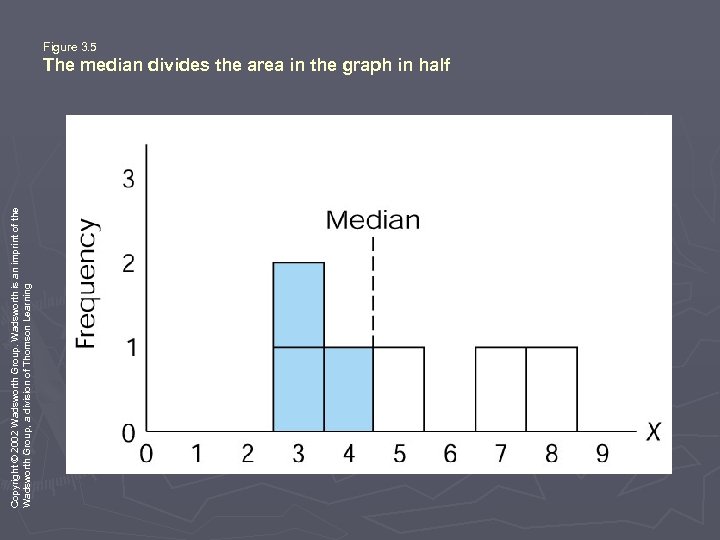Copyright © 2002 Wadsworth Group. Wadsworth is an imprint of the Wadsworth Group, a division of Thomson Learning Figure 3. 5 The median divides the area in the graph in half

Mode ► The score or category that has the greatest frequency ► No symbols or notation to identify the mode ► The definition is the same for either a population or a sample distribution.

Mode (cont. ) ► Can be used to determine the typical or average value for any scale of measurement, including a nominal scale (chapter 1) ► It is possible to have more than one mode

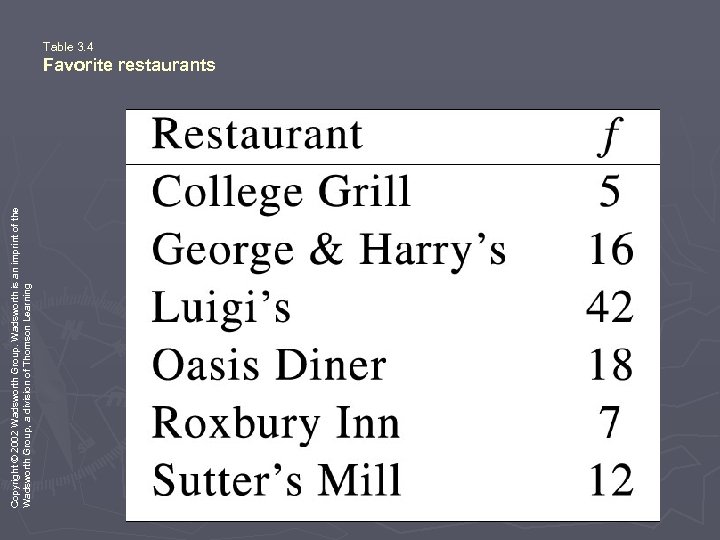Copyright © 2002 Wadsworth Group. Wadsworth is an imprint of the Wadsworth Group, a division of Thomson Learning Table 3. 4 Favorite restaurants

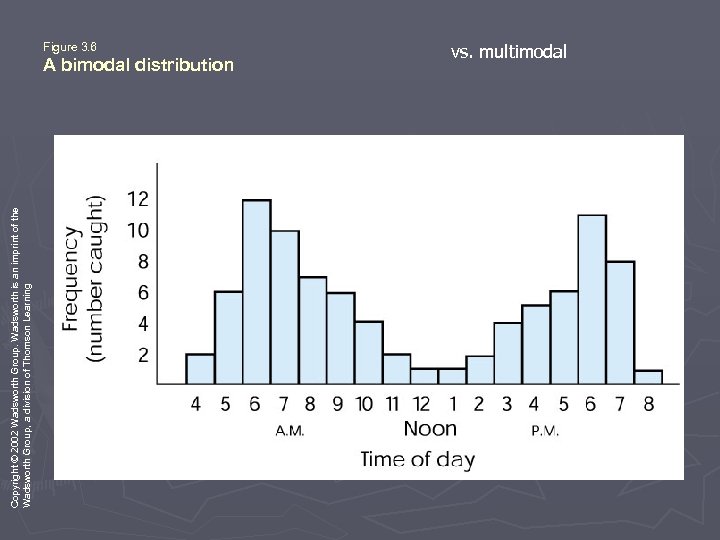Copyright © 2002 Wadsworth Group. Wadsworth is an imprint of the Wadsworth Group, a division of Thomson Learning Figure 3. 6 A bimodal distribution vs. multimodal

Selecting a Measure of Central Tendency ► Could be possible to compute two or three measures of central tendency with a set of data. ► Often get similar results.

Mean ► Mean is the most preferred measure. § Usually a good representative value § Goal is to find the single value that best represents the entire distribution. ► Mean has the added advantage of being closely related to variance and standard deviation (the most common measures of variability) ► This relationship makes the mean a valuable measure for purposes of inferential statistics

When to Use the Median ► Three Page 68 situations in which the median serves as a valuable alternative to the mean. § Extreme scores or skewed distributions § Undetermined values § Open-ended distributions

When to Use the Mode ► Three situations in which the mode is commonly used as an alternative to the mean, or is used in conjunction with the mean to describe central tendency § Nominal scales § Discrete variables § Describing shape

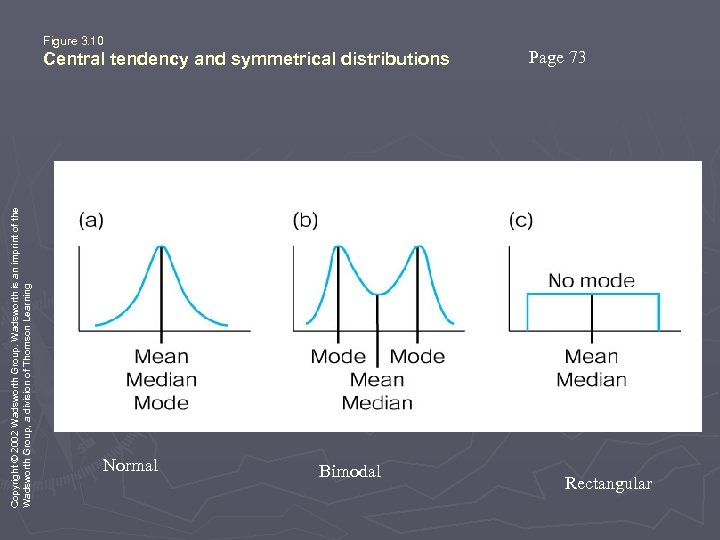Copyright © 2002 Wadsworth Group. Wadsworth is an imprint of the Wadsworth Group, a division of Thomson Learning Figure 3. 10 Central tendency and symmetrical distributions Normal Bimodal Page 73 Rectangular

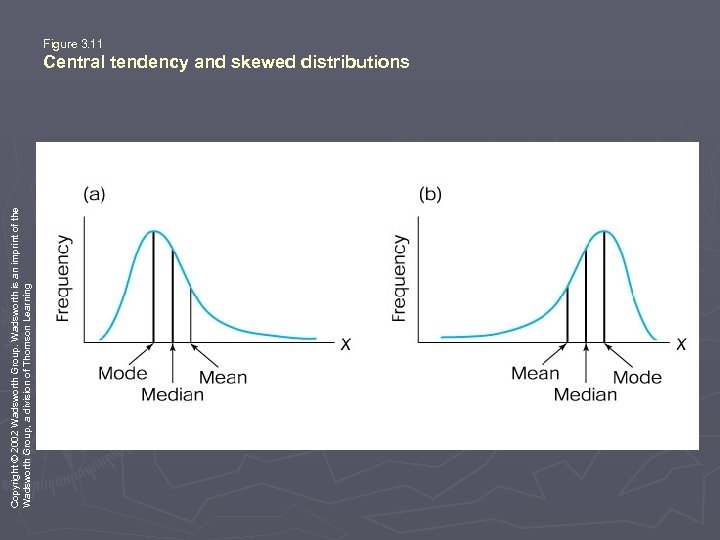Copyright © 2002 Wadsworth Group. Wadsworth is an imprint of the Wadsworth Group, a division of Thomson Learning Figure 3. 11 Central tendency and skewed distributions