Chapter 3 Determining Height of KM Introduction

Chapter 3 Determining Height of KM

Introduction Accurate KM can not be made except by the naval architect KM for the vessel is readily available to the ship’s officer

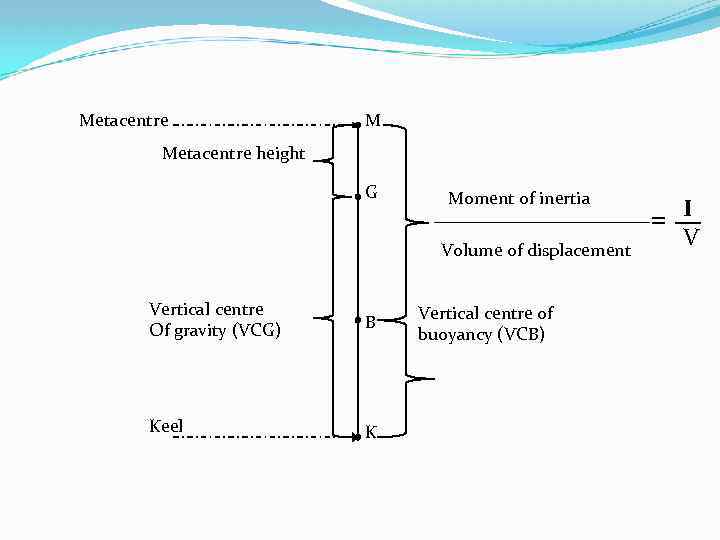Metacentre M Metacentre height G Moment of inertia Volume of displacement Vertical centre Of gravity (VCG) B Keel K Vertical centre of buoyancy (VCB) = I V

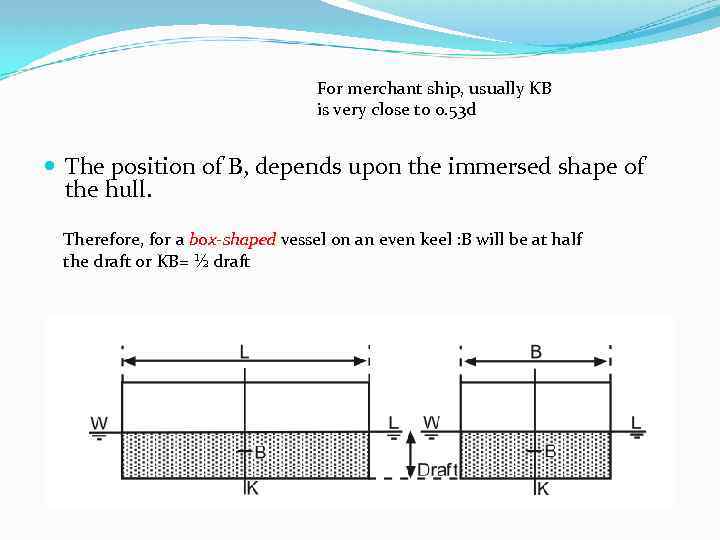For merchant ship, usually KB is very close to 0. 53 d The position of B, depends upon the immersed shape of the hull. Therefore, for a box-shaped vessel on an even keel : B will be at half the draft or KB= ½ draft

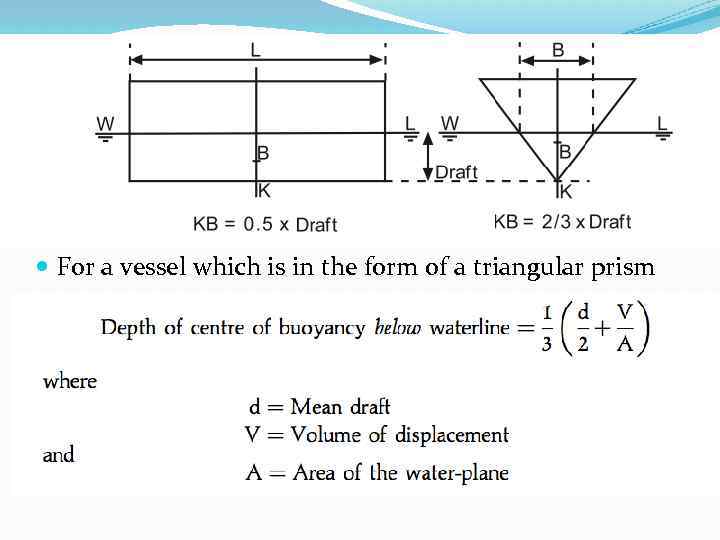For a vessel which is in the form of a triangular prism KB = 2/3 x Draft

For ordinary ship can be obtained by using Morrish’s Formula

Calculating BM is also called metacentric radius. The formula commonly used for calculating BM=I/ I= the moment of inertia (about a longitudinal axis of the water plan, in units of feet 4 or meter 4) = the volume of displacement, in units of feet 3 or meter 3

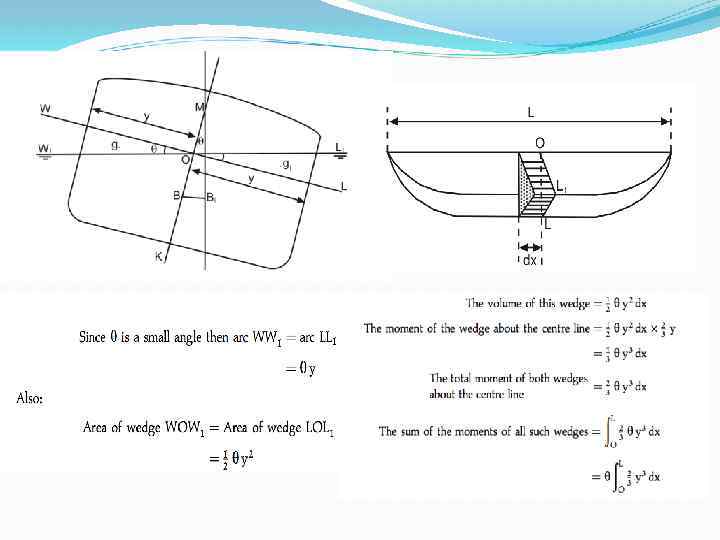
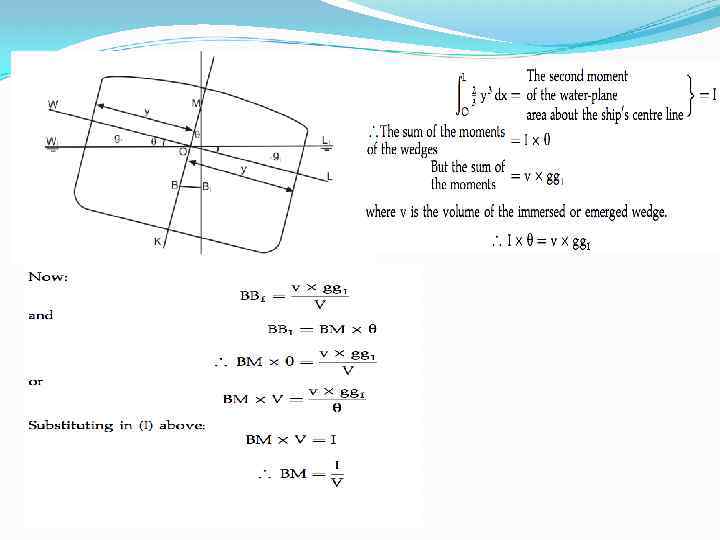
Moment of inertia I= (LB 3)/12 L= length of the water plane B= the breath of the water plane 12= a constant for a rectangular shape For a box-shaped vessel: BM = I/V=LB 3/12 V B=beam of vessel, d=any draft of ship B=breath at the waterline, d is the corresponding draft

For approximating moment of inertia for a ship’s water plane I =LB 3 k K is a constant depending upon the value of Cw Water plane coefficient (Cw) K 0. 70 0. 042 0. 75 0. 048 0. 80 0. 055 0. 85 0. 062 Beam is the important factors of initial stability.

Example 1 A box-shaped vessel is 24 m x 5 m and floats on an even keel at 2 m draft. KG= 1. 5 m. Calculate the initial metacentric height. KB= ½ draft BM= B 2/12 d KB= 1 m BM= 52/(12 x 2) = 1. 04 m KM= KB + BM = 2. 04 m GM= KM- KG = 2. 04 – 1. 50 = 0. 54 m

Example 2 The moment of inertia of a ship’s water plane are about the center line is 20, 000 m 4 units. The displacemnet is 7000 tonnes whist floating in dock water of density 1008 kg per cu. m. KB= 1. 9 m, and KG= 3. 2 m. Calculate the initial metacentric height. KM = KB + BM = 1. 9 m + 2. 88 m = 4. 78 m GM = KM – KG= 4. 78 m – 3. 2 = + 1. 58 m

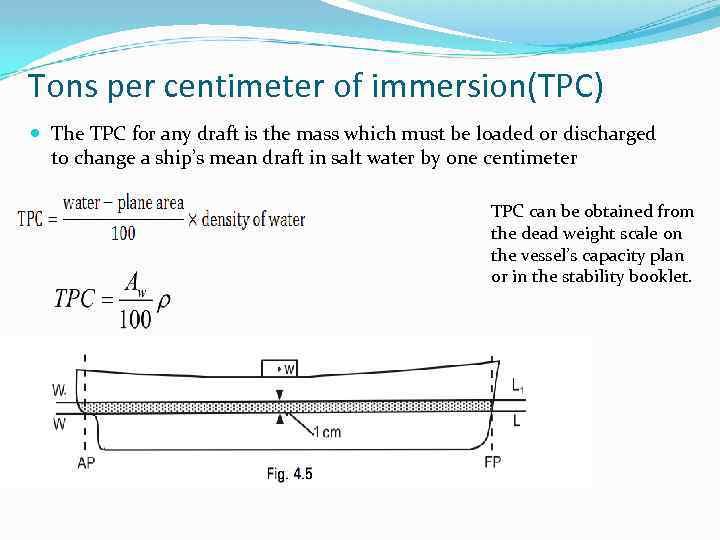Tons per centimeter of immersion(TPC) The TPC for any draft is the mass which must be loaded or discharged to change a ship’s mean draft in salt water by one centimeter TPC can be obtained from the dead weight scale on the vessel’s capacity plan or in the stability booklet.

Example 1 The water plane area of ship is 1500 m 2 Calculate TPC in fresh water and sea water? TPCF =

Fresh water Allowance (FWA) The fresh water allowance is the number of millimeters by which the mean draft changes when a ship passes from salt water to fresh water, or vice versa, whilst floating at the loaded draft

Let V be volume of salt water displaced at this draft, v be the extra volume of water displaced in fresh water Mass of SW displaced = 1025 V Mass of FW displaced = 1000(V + v) FW displaced = mass of SW displaced Then, 1000 (V + v) = 1025 V v = V/40 W and w is the mass of salt water in volume V and v, in tons So, w= W/40 W= loaded salt water displacement

Example 1 A ship is loading in dock water of density 1010 kg per cu. m. FWA= 150 mm. Find the change in draft on entering salt water. Let x = the change in draft in millimeters X=150 x 15/25, x= 90 mm Draft will decrease by 90 mm

Example 2 A vessel is floating at a draft of 10. 10 meters in salt water. Her length on the load water is 210. 0 meters beam is 30. 0 meters. TPC is 52. 22 metric tons per centimeter. Displacement is 40, 778 metric tons. Find approximately KM. Cw =Aw/LB=5094. 63/6300=0. 809 m 2 Water plane coefficient K 0. 70 0. 042 V = displacement in metric tons /1. 025 =39, 783. 41 meters 3 BM = I/ V =317, 520. 0 meter 4 /39, 783. 41 meters 3 =7. 98 meters 0. 75 0. 048 KB= 0. 53(draft)=0. 53 (10. 10 meters) = 5. 35 meters 0. 80 0. 055 Approximate KM= KB + BM = 7. 98 + 5. 35 = 13. 33 meters 0. 85 0. 062 I =LB 3 k=(210 meters)(30 meters)3(0. 056)=317, 5200 meters

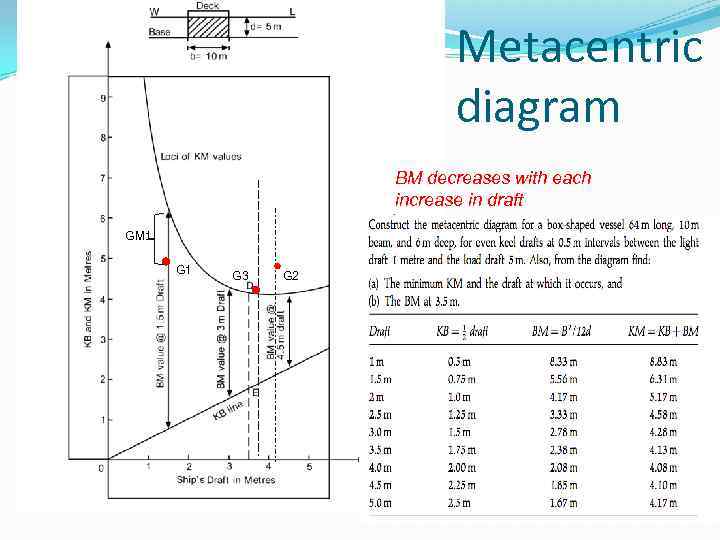Metacentric diagram BM decreases with each increase in draft GM 1 G 3 G 2

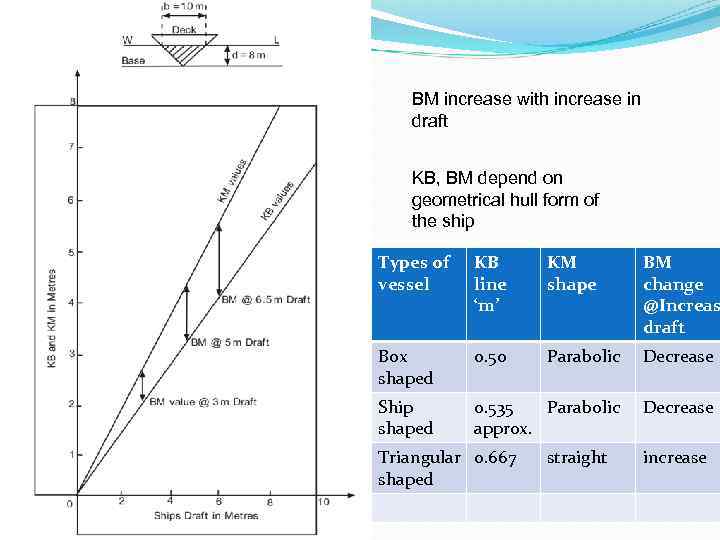BM increase with increase in draft KB, BM depend on geometrical hull form of the ship Types of vessel KB line ‘m’ KM shape BM change @Increas draft Box shaped 0. 50 Parabolic Decrease Ship shaped 0. 535 Parabolic approx. Decrease Triangular 0. 667 shaped straight increase

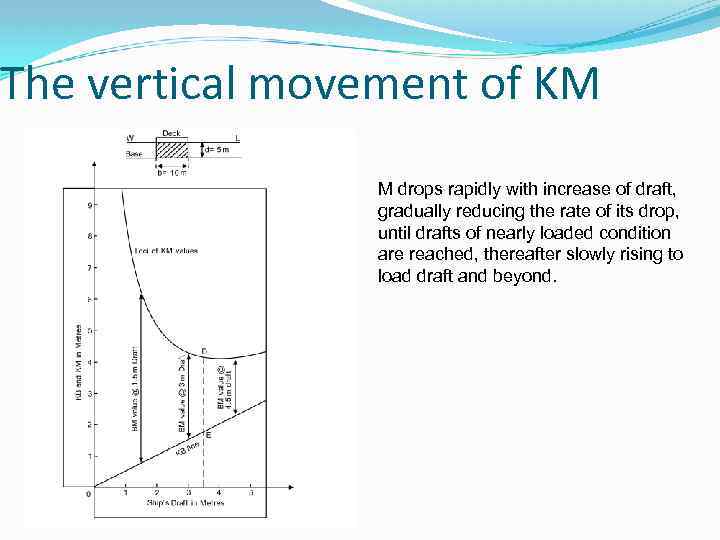The vertical movement of KM M drops rapidly with increase of draft, gradually reducing the rate of its drop, until drafts of nearly loaded condition are reached, thereafter slowly rising to load draft and beyond.

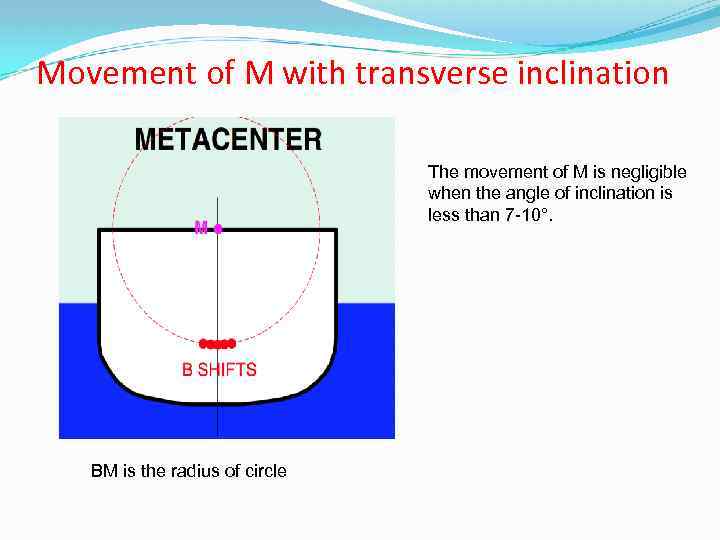Movement of M with transverse inclination The movement of M is negligible when the angle of inclination is less than 7 -10°. BM is the radius of circle

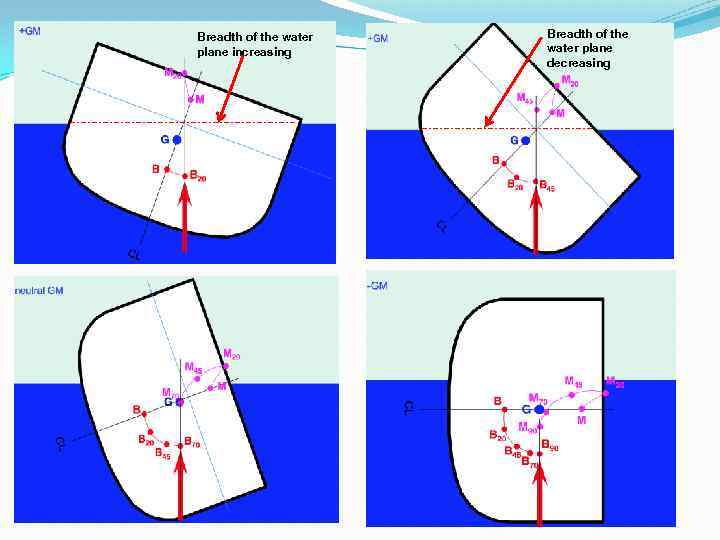Breadth of the water plane increasing Breadth of the water plane decreasing

Conclusions GM= KM – KG = KB + BM - KG Increasing of BM Decreasing of KG GM increase Decremnt of BM > decrement of KG GM decrease Decrement of BM < decrement of KG GM increase

Discussions GM= KM – KG = KB + BM - KG Decreasing of BM Increasing of KG GM ? Increment of BM > Increment of KG GM ? Increment of BM < Increment of KG GM ?