Chapter 3 DECISION ANALYSIS Part 2 1

Chapter 3: DECISION ANALYSIS Part 2 1

Decision Making Under Risk § Probabilistic decision situation § States of nature have probabilities of occurrence. § The probability estimate for the occurrence of each state of nature( if available) can be incorporated in the search for the optimal decision. § For each decision calculate its expected payoff by S (Probability)(Payoff) Expected Payoff = Over States of Nature 2

Decision Making Under Risk (cont. ) § Select the decision with the best expected payoff 3

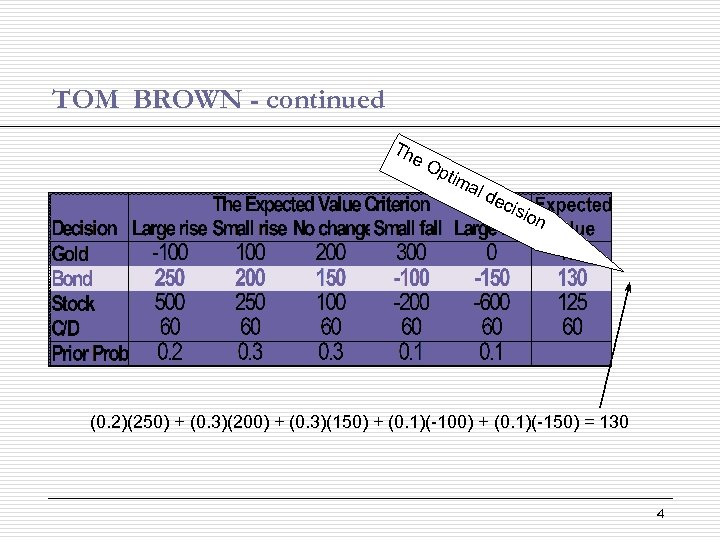TOM BROWN - continued Th e. O ptim al d e cis io n (0. 2)(250) + (0. 3)(200) + (0. 3)(150) + (0. 1)(-100) + (0. 1)(-150) = 130 4

Decision Making Criteria (cont. ) § When to Use the Expected Value Approach § The Expected Value Criterion is useful in cases where long run planning is appropriate, and decision situations repeat themselves. § One problem with this criterion is that it does not consider attitude toward possible losses. 5

Expected Value of Perfect Information § The gain in Expected Return obtained from knowing with certainty the future state of nature is called: Expected Value of Perfect Information (EVPI) § It is also the Smallest Expect Regret of any decision alternative. Therefore, the EVPI is the expected regret corresponding to the decision selected using the expected value criterion 6

Expected Value of Perfect Information (cont. ) § EVPI = ERPI - EREV § EREV: Expected Return of the EV criterion. § Expected Return with Perfect Information ERPI= (best outcome of 1 st state of nature)*(Probability of 1 st state of nature) + …. . +(best outcome of last state of nature)*(Probability of last state of nature) 7

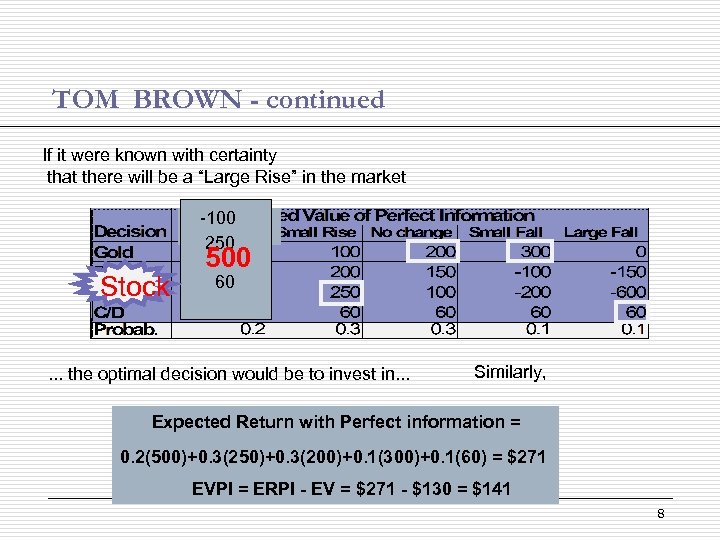TOM BROWN - continued If it were known with certainty that there will be a “Large Rise” in the market -100 Large rise 250 Stock 500 60 . . . the optimal decision would be to invest in. . . Similarly, Expected Return with Perfect information = 0. 2(500)+0. 3(250)+0. 3(200)+0. 1(300)+0. 1(60) = $271 EVPI = ERPI - EV = $271 - $130 = $141 8

Expected Value of Perfect Information (cont. ) § Another way to determine EVPI as follows If Tom knows the market will show a large rise, he should buy the “stock”, within profit $500, or a gain of $250 over what he would earn from the “bond” (optimal decision without the additional information). 9

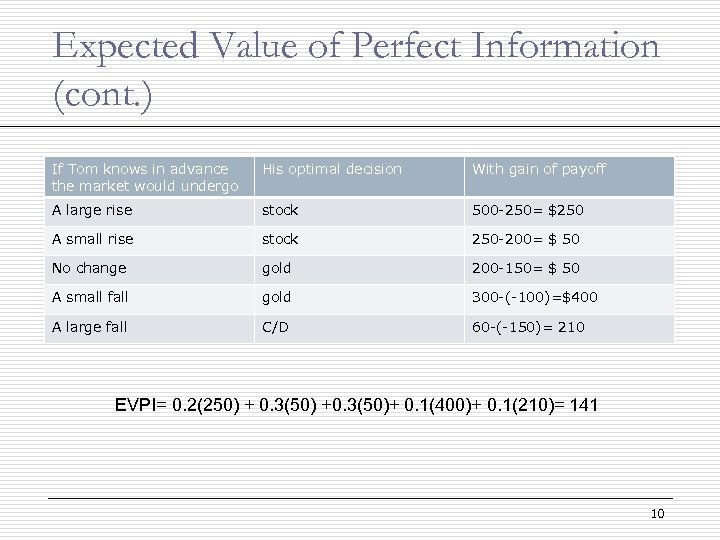Expected Value of Perfect Information (cont. ) If Tom knows in advance the market would undergo His optimal decision With gain of payoff A large rise stock 500 -250= $250 A small rise stock 250 -200= $ 50 No change gold 200 -150= $ 50 A small fall gold 300 -(-100)=$400 A large fall C/D 60 -(-150)= 210 EVPI= 0. 2(250) + 0. 3(50) +0. 3(50)+ 0. 1(400)+ 0. 1(210)= 141 10

Baysian Analysis - Decision Making with Imperfect Information § Baysian Statistic play a role in assessing additional information obtained from various sources. § This additional information may assist in refining original probability estimates, and help improve decision making. 11

TOM BROWN - continued § Tom can purchase econometric forecast results for $50. § The forecast predicts “negative” or “positive” econometric growth. § Statistics regarding the forecast. When the stock market showed a large rise the forecast was “positive growth” 80% of the time. 12

TOM BROWN - continued § P(forecast predicts “positive” | small rise in market) = 0. 7 § P(forecast predicts “ negative” | small rise in market) = 0. 3 Should Tom purchase the Forecast ? 13

SOLUTION § Tom should determine his optimal decisions when the forecast is “positive” and “negative”. § If his decisions change because of the forecast, he should compare the expected payoff with and without the forecast. § If the expected gain resulting from the decisions made with the forecast exceeds $50, he should purchase the forecast. 14

SOLUTION § To find Expected payoff with forecast Tom should determine what to do when: § The forecast is “positive growth” § The forecast is “negative growth” 15

SOLUTION § Tom needs to know the following probabilities § § § P(Large rise | The forecast predicted “Positive”) P(Small rise | The forecast predicted “Positive”) P(No change | The forecast predicted “Positive ”) P(Small fall | The forecast predicted “Positive”) P(Large Fall | The forecast predicted “Positive”) 16

SOLUTION § § § P(Large rise | The forecast predicted “Negative ”) P(Small rise | The forecast predicted “Negative”) P(No change | The forecast predicted “Negative”) P(Small fall | The forecast predicted “Negative”) P(Large Fall) | The forecast predicted “Negative”) Bayes’ Theorem provides a procedure to calculate these probabilities 17

Bayes’ Theorem § P(A|B) = § Proof: p(A|B)= P (A and B) / P(B) (1) P(B|A)= P(A and B)/P(A) P(A and B) = P(B|A)*P(A) (1) P(A|B)=P(B|A)*P(A)/P(B) 18

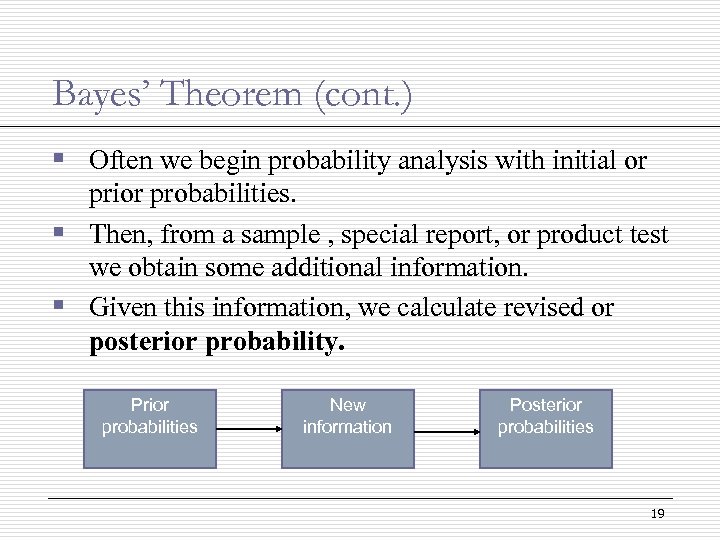Bayes’ Theorem (cont. ) § Often we begin probability analysis with initial or prior probabilities. § Then, from a sample , special report, or product test we obtain some additional information. § Given this information, we calculate revised or posterior probability. Prior probabilities New information Posterior probabilities 19

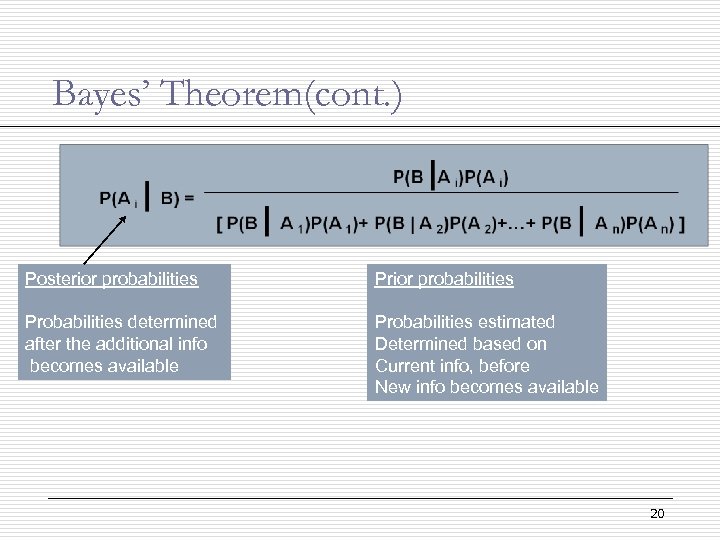Bayes’ Theorem(cont. ) Posterior probabilities Probabilities determined after the additional info becomes available Probabilities estimated Determined based on Current info, before New info becomes available 20

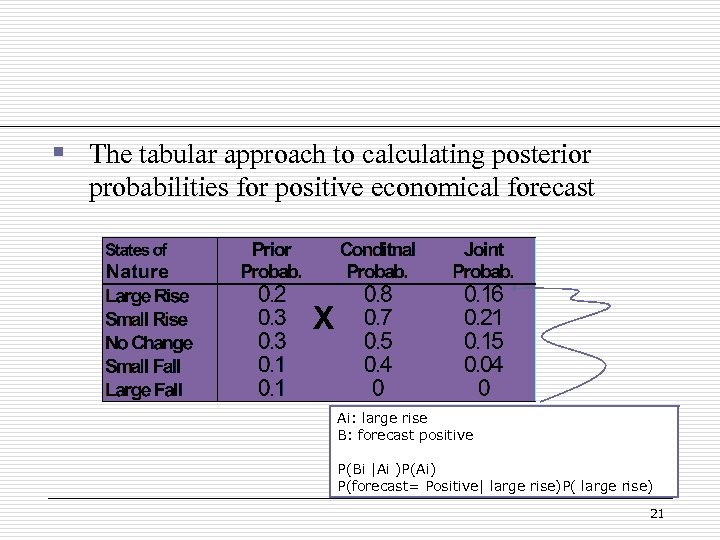§ The tabular approach to calculating posterior probabilities for positive economical forecast X Ai: large rise B: forecast positive P(Bi |Ai )P(Ai) P(forecast= Positive| large rise)P( large rise) 21

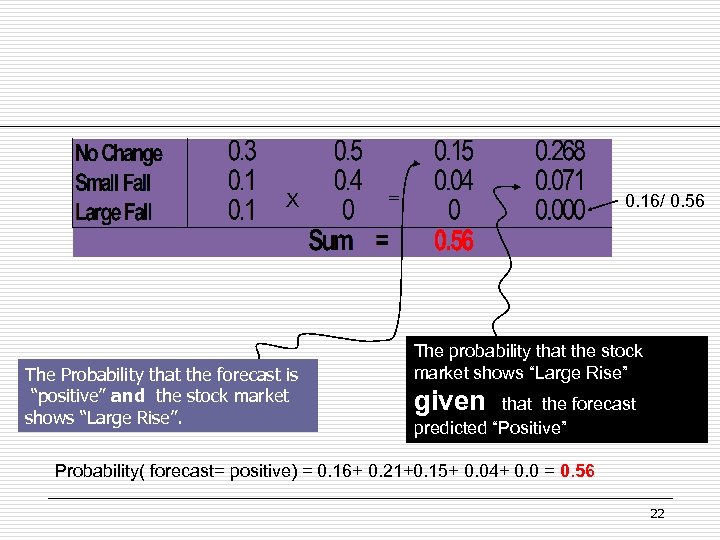X The Probability that the forecast is “positive” and the stock market shows “Large Rise”. = 0. 16/ 0. 56 The probability that the stock market shows “Large Rise” given that the forecast predicted “Positive” Probability( forecast= positive) = 0. 16+ 0. 21+0. 15+ 0. 04+ 0. 0 = 0. 56 22

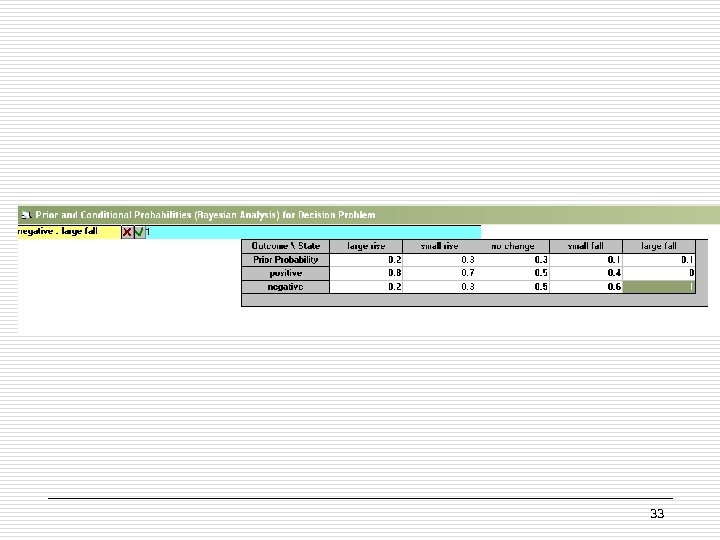
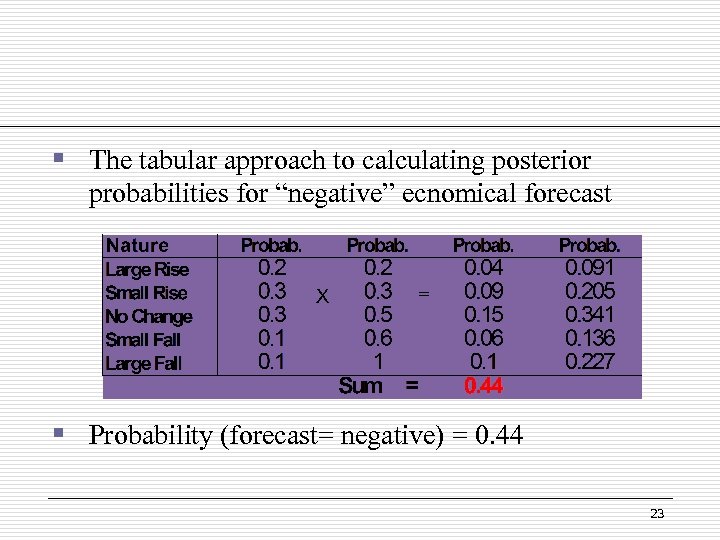§ The tabular approach to calculating posterior probabilities for “negative” ecnomical forecast X = § Probability (forecast= negative) = 0. 44 23

WINQSB printout for the calculation of the Posterior probabilities 24

25

26

27

28

29

30

31

32

33

34

35

Expected Value of Sample Information EVSI § gain from making decisions based on Sample Information. § With the forecast available, the Expected Value of Return is revised. § Calculate Revised Expected Values for a given Gold forecast Bond -100 200 300 00 -100 250 200 150 200 -100 300 -150 $180 as follows. 100 $84 -100 200 300 0 EV(Invest in……. |“Positive” forecast) = Gold -100 Bond 100 200 300 =. 286( )+. 375( )+. 268( )+. 071( 250 100 200 150 -100 300 ) = -100 0 -150 0 )+0( $120 $ 65 36

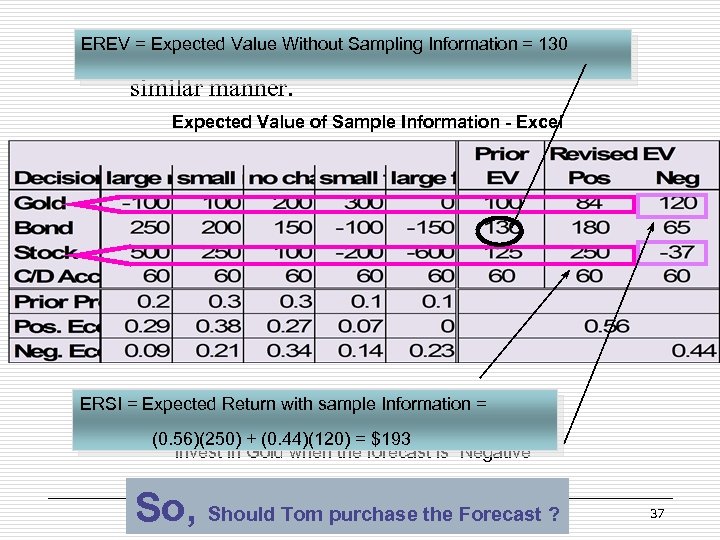EREV = Expected of the revised EV s. Information = 130 § The rest Value Without Sampling are calculated in a similar manner. Expected Value of Sample Information - Excel Invest Expected Return Forecast is Information ERSI =in Stock when the with sample “Positive” = (0. 56)(250) + (0. 44)(120) = $193 Invest in Gold when the forecast is “Negative” So, Should Tom purchase the Forecast ? 37

§ EVSI = Expected Value of Sampling Information = ERSI - EREV = 193 - 130 = $63. Yes, Tom should purchase the Forecast. His expected return is greater than the Forecast cost. § Efficiency = EVSI / EVPI = 63 / 141 = 0. 45 38

Game Theory § Game theory can be used to determine optimal decision in face of other decision making players. § All the players are seeking to maximize their return. § The payoff is based on the actions taken by all the decision making players. 39

Game Theory (cont. ) § Classification of Games § Number of Players § Two players - Chess § Multiplayer - More than two competitors (Poker) § Total return § Zero Sum - The amount won and amount lost by all competitors are equal (Poker among friends) § Nonzero Sum -The amount won and the amount lost by all competitors are not equal (Poker In A Casino) 40

Game Theory (cont. ) § Sequence of Moves § Sequential - Each player gets a play in a given sequence. § Simultaneous - All players play simultaneously. 41