Chapter 22 Electric Field 22 1 What is

Chapter 22 Electric Field 22. 1. What is Physics? 22. 2. The Electric Field 22. 3. Electric Field Lines 22. 4. The Electric Field Due to a Point Charge 22. 5. The Electric Field Due to an Electric Dipole 22. 6. The Electric Field Due to a Line of Charge 22. 7. The Electric Field Due to a Charged Disk 22. 8. A Point Charge in an Electric Field 22. 9. A Dipole in an Electric Field

The Electric Field We bring in a positive charge q 0 as a test charge, which is carefully selected with a very small magnitude, so that it does not alter the locations of the other charges How does particle q 0 “know” of the presence of other charge?

THE ELECTRIC FIELD The electric field E that exists at a point is the electrostatic force F experienced by a small test charge q 0 placed at that point divided by the charge itself: The electric field is a vector, and its direction is the same as the direction of the force F on a positive test charge • SI Unit of Electric Field: newton per coulomb (N/C) •

Important about electric field • It is the surrounding charges that create an electric field at a given point. • Any charge q placed at the point with the electric field E will experiences a force, F=q. E. For a positive charge, the force points in the same direction as the electric field; for a negative charge, the force points in the opposite direction as the electric field. • At a particular point in space, each of the surrounding charges contributes to the net electric field that exists there

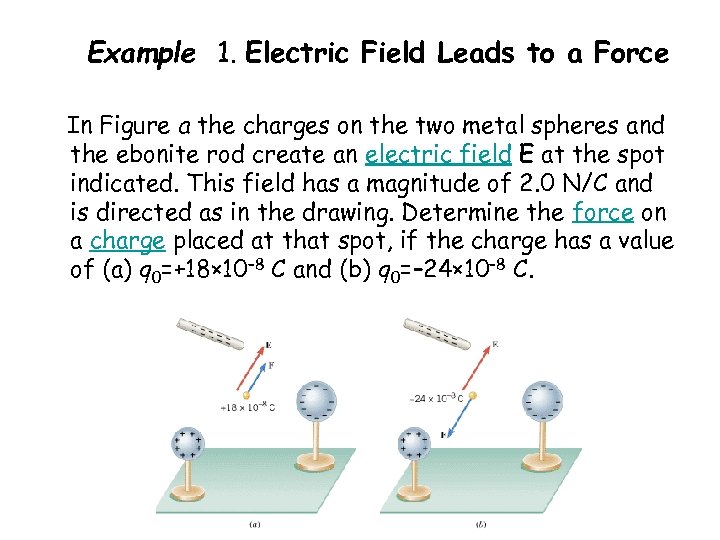Example 1. Electric Field Leads to a Force In Figure a the charges on the two metal spheres and the ebonite rod create an electric field E at the spot indicated. This field has a magnitude of 2. 0 N/C and is directed as in the drawing. Determine the force on a charge placed at that spot, if the charge has a value of (a) q 0=+18× 10– 8 C and (b) q 0=– 24× 10– 8 C.

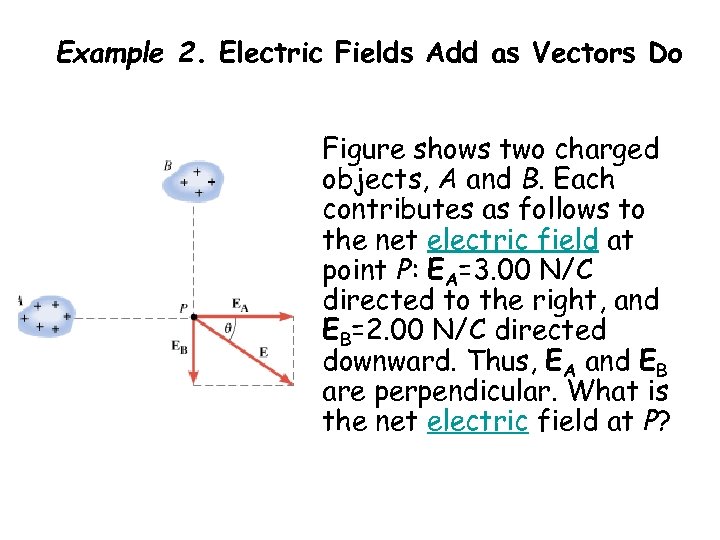Example 2. Electric Fields Add as Vectors Do Figure shows two charged objects, A and B. Each contributes as follows to the net electric field at point P: EA=3. 00 N/C directed to the right, and EB=2. 00 N/C directed downward. Thus, EA and EB are perpendicular. What is the net electric field at P?

Example 3. The Electric Field of a Point Charge There is an isolated point charge of q=+15 μC in a vacuum. Using a test charge of q 0=+0. 80 μC, determine the electric field at point P, which is 0. 20 m away.

Properties of electric field by a point charge (1) The magnitude of electric field by a point charge is given by (2) If q is positive, then E is directed away from q, as in Figure b. On the other hand, if q is negative, then E is directed toward q.

Check Your Understanding A positive point charge +q is fixed in position at the center of a square, as the drawing shows. A second point charge is fixed to either corner B, corner C, or corner D. The net electric field at corner A is zero. (a) At which corner is the second charge located? (b) Is the second charge positive or negative? (c) Does the second charge have a greater, (a) smaller, or the same magnitude as the charge at the center?

Example 4. The Electric Fields from Separate Charges May Cancel Two positive point charges, q 1=+16 μC and q 2=+4. 0 μC, are separated in a vacuum by a distance of 3. 0 m, as Figure illustrates. Find the spot on the line between the charges where the net electric field is zero.

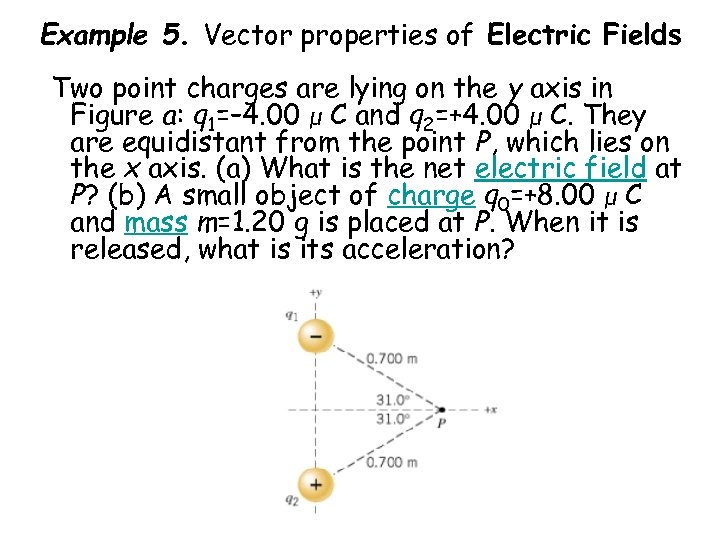Example 5. Vector properties of Electric Fields Two point charges are lying on the y axis in Figure a: q 1=– 4. 00 μ C and q 2=+4. 00 μ C. They are equidistant from the point P, which lies on the x axis. (a) What is the net electric field at P? (b) A small object of charge q 0=+8. 00 μ C and mass m=1. 20 g is placed at P. When it is released, what is its acceleration?

Electric Field Lines The electric charges create an electric field in the space surrounding them. It is useful to have a kind of “map” that gives the direction and indicates the strength of the field at various places. This can be done by drawing the electric field lines.

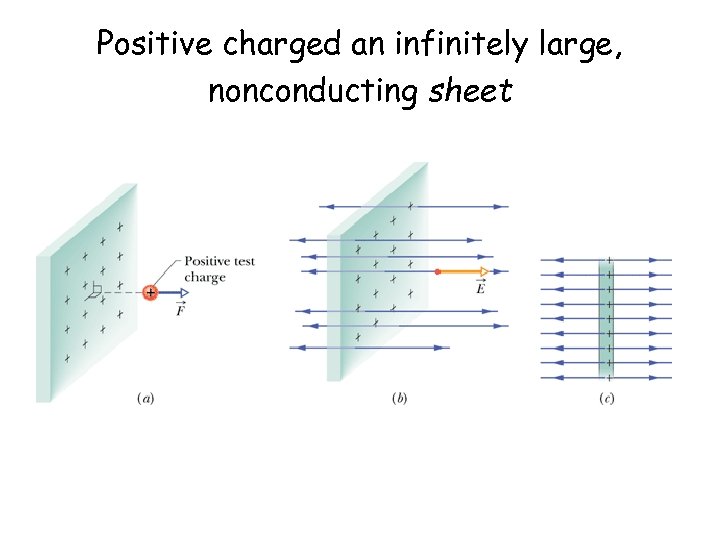Positive charged an infinitely large, nonconducting sheet

The properties of the electric field lines • At any point, the tangent direction of the electric line is the direction of electric field. • The density of the electric field lines provides information about the magnitude of the field. The lines are closer together where the electric field is stronger, the lines are closer together. The lines are more spread out where the electric field is weaker. • The electric field lines always begin on a positive charge and end on a negative charge and do not start or stop in midspace.

Electric Dipole • two charged particles of magnitude q but of opposite sign, separated by a distance d. We call this configuration an electric dipole • The product qd, which involves the two intrinsic properties q and d of the dipole, is the magnitude p of a vector quantity known as the electric dipole moment of the dipole. The direction of P is taken to be from the negative to the positive end of the dipole

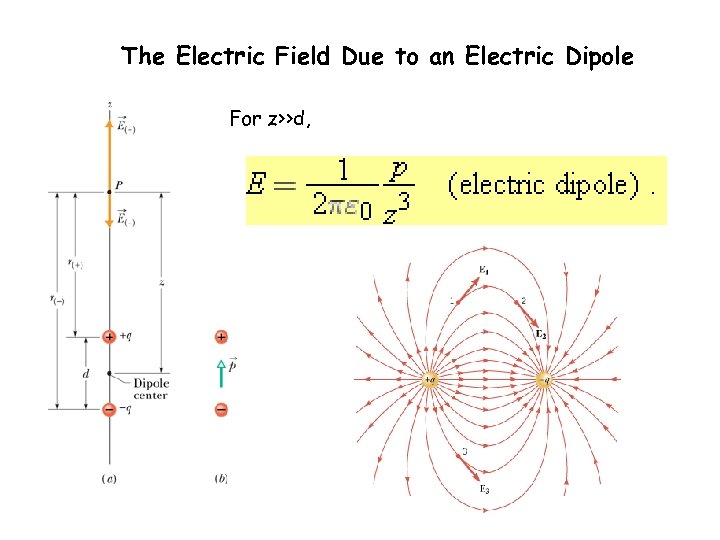The Electric Field Due to an Electric Dipole For z>>d,

The Electric Field Inside a Conductor: Shielding (1) At equilibrium under electrostatic conditions, any excess charge resides on the surface of a conductor.

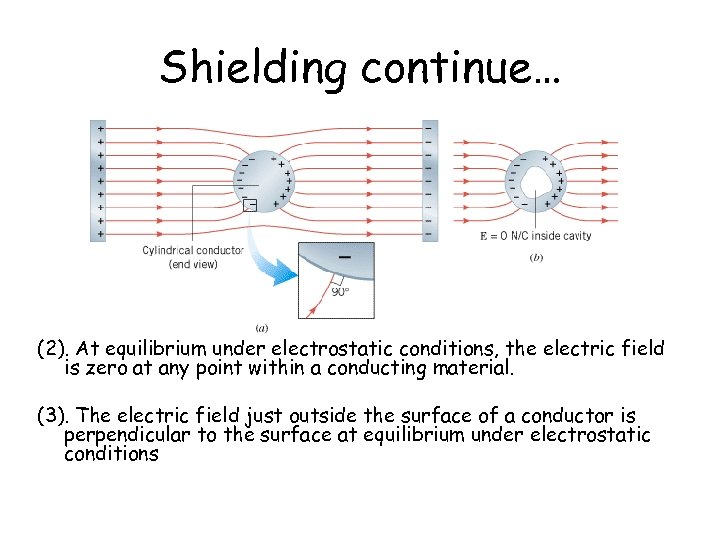Shielding continue… (2). At equilibrium under electrostatic conditions, the electric field is zero at any point within a conducting material. (3). The electric field just outside the surface of a conductor is perpendicular to the surface at equilibrium under electrostatic conditions

The Electric Field Due to a Line of Charge Name Symbol SI Unit Charge q C Linear charge density λ C/m Surface charge density σ C/m 2 Volume charge density ρ C/m 3

Electric field of a ring of uniform positive charge

The Electric Field Due to a Charged Disk For infinite sheet, R ∞,

Sample Problem: A Point Charge in an Electric Field Figure shows the deflecting plates of an ink-jet printer, with superimposed coordinate axes. An ink drop with a mass m of 1. 3 x 10 -10 kg and a negative charge of magnitude Q=1. 5 x 10 -13 C enters the region between the plates, initially moving along the x axis with speed vx=18 m/s. The length L of each plate is 1. 6 cm. The plates are charged and thus produce an electric field at all points between them. Assume that field E is downward directed, is uniform, and has a magnitude of 1. 4 x 106 N/C. What is the vertical deflection of the drop at the far edge of the plates? (The gravitational force on the drop is small relative to the electrostatic force acting on the drop and can be neglected. )

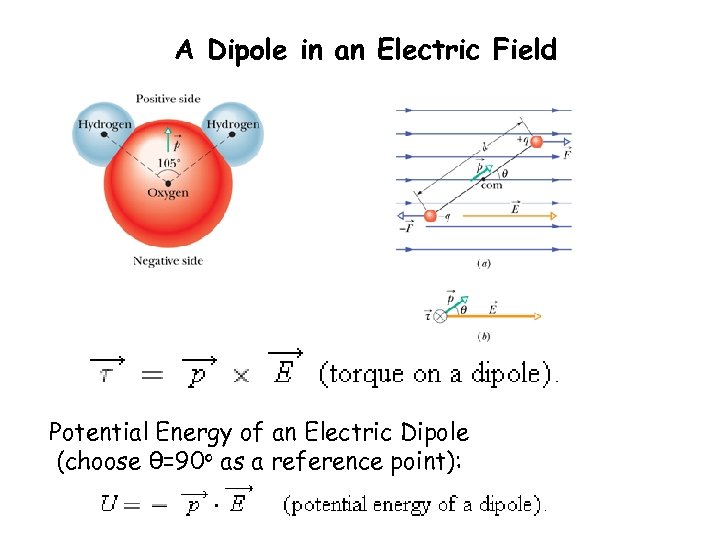A Dipole in an Electric Field Potential Energy of an Electric Dipole (choose θ=90 o as a reference point):

Sample Problem A neutral water molecule H 2 O in its vapor state has an electric dipole moment of magnitude 6. 2 x 10 -30 c. m. (a) How far apart are the molecule's centers of positive and negative charge? (b) If the molecule is placed in an electric field of 1. 5 x 104 N/c , what maximum torque can the field exert on it? (Such a field can easily be set up in the laboratory. ) (c) How much work must an external agent do to rotate this molecule by 180 o in this field, starting from its fully aligned position, for which θ=0?

Conceptual Questions (1) (2) (3) A proton and an electron are held in place on the x axis. The proton is at x=–d, while the electron is at x=+d. They are released simultaneously, and the only force that affects their motions is the electrostatic force of attraction that each applies to the other. Which particle reaches the origin first? Give your reasoning. On a thin, nonconducting rod, positive charges are spread evenly, so that there is the same amount of charge per unit length at every point. On another identical rod, positive charges are spread evenly over only the left half, and the same amount of negative charges are spread evenly over the right half. For each rod, deduce the direction of the electric field at a point that is located directly above the midpoint of the rod. Give your reasoning. There is an electric field at point P. A very small charge is placed at this point and experiences a force. Another very small charge is then placed at this point and experiences a force that differs in both magnitude and direction from that experienced by the first charge. How can these two different forces result from the single electric field that exists at point P?

(4) Drawings I and II show two examples of electric field lines. Decide which of the following statements are true and which are false, defending your choice in each case. (a) In both I and II the electric field is the same everywhere. (b) As you move from left to right in each case, the electric field becomes stronger. (c) The electric field in I is the same everywhere but becomes stronger in II as you move from left to right. (d) The electric fields in both I and II could be created by negative charges located somewhere on the left and positive charges somewhere on the right. (e) Both I and II arise from a single positive point charge located somewhere on the left.

(5) A positively charged particle is moving horizontally when it enters the region between the plates of a capacitor, as the drawing illustrates. (a) Draw the trajectory that the particle follows in moving through the capacitor. (b) When the particle is within the capacitor, which of the following four vectors, if any, are parallel to the electric field inside the capacitor: the particle’s displacement, its velocity, its linear momentum, its acceleration? For each vector explain why the vector is, or is not, parallel to the electric field of the capacitor.