Chapter 20 International Portfolio Theory and Diversification Copyright

Chapter 20 International Portfolio Theory and Diversification Copyright © 2004 Pearson Addison-Wesley. All rights reserved.

International Diversification and Risk • The case for international diversification of portfolios can be decomposed into two components, the first of which is the potential risk reduction benefits of holding international securities. • This initial focus is on risk. • The risk of a portfolio is measured by the ratio of the variance of a portfolio’s return relative to the variance of the market return (portfolio beta). • As an investor increases the number of securities in a portfolio, the portfolio’s risk declines rapidly at first, then asymptotically approaches the level of systematic risk of the market. • A domestic portfolio that is fully diversified would have a beta of 1. 0. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 2

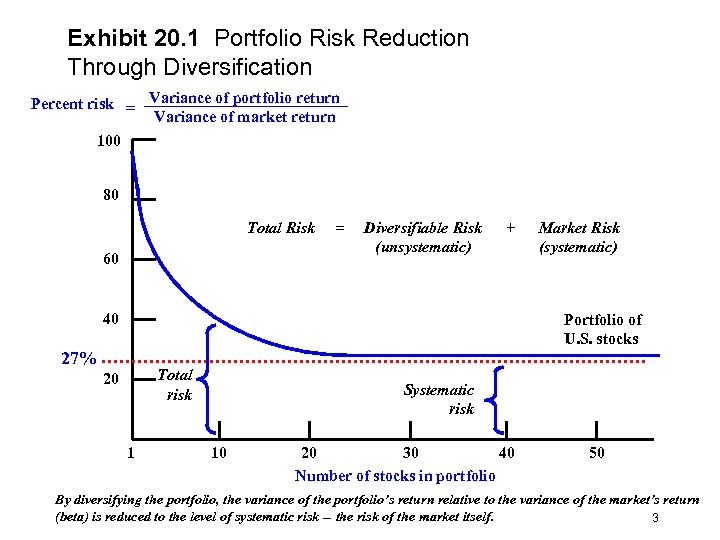Exhibit 20. 1 Portfolio Risk Reduction Through Diversification Percent risk = Variance of portfolio return Variance of market return 100 80 Total Risk 60 = Diversifiable Risk (unsystematic) + 40 Market Risk (systematic) Portfolio of U. S. stocks 27% Total risk 20 1 Systematic risk 10 20 30 40 Number of stocks in portfolio 50 By diversifying the portfolio, the variance of the portfolio’s return relative to the variance of the market’s return (beta) is reduced to the level of systematic risk -- the risk of the market itself. 3

International Diversification and Risk • The total risk of any portfolio is therefore composed of systematic risk (the market) and unsystematic risk (the individual securities). • Increasing the number of securities in the portfolio reduces the unsystematic risk component leaving the systematic risk component unchanged. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 4

International Diversification and Risk • The second component of the case for international diversification addresses foreign exchange risk. • The foreign exchange risks of a portfolio, whether it be a securities portfolio or the general portfolio of activities of the MNE, are reduced through international diversification. • Purchasing assets in foreign markets, in foreign currencies may alter the correlations associated with securities in different countries (and currencies). • This provides portfolio composition and diversification possibilities that domestic investment and portfolio construction may not provide. • The risk associated with international diversification, when it includes currency risk, is very complicated when compared to domestic investments. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 5

International Diversification and Risk • International diversification benefits induce investors to demand foreign securities (the so called buy-side). • If the addition of a foreign security to the portfolio of the investor aids in the reduction of risk for a given level of return, or if it increases the expected return for a given level of risk, then the security adds value to the portfolio. • A security that adds value will be demanded by investors, bidding up the price of that security, resulting in a lower cost of capital for the issuing firm. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 6

Internationalizing the Domestic Portfolio • Classic portfolio theory assumes a typical investor is risk-averse. • This means an investor is willing to accept some risk but is not willing to bear unnecessary risk. • The typical investor is therefore in search of a portfolio that maximizes expected portfolio return per unit of expected portfolio risk. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 7

Internationalizing the Domestic Portfolio • The domestic investor may choose among a set of individual securities in the domestic market. • The near-infinite set of portfolio combinations of domestic securities form the domestic portfolio opportunity set (next exhibit). • The set of portfolios along the extreme left edge of the set is termed the efficient frontier. • This efficient frontier represents the optimal portfolios of securities that possess the minimum expected risk for each level of expected portfolio return. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 8

Internationalizing the Domestic Portfolio • The portfolio with the minimum risk along all those possible is the minimum risk domestic portfolio (MRDP). • The individual investor will search out the optimal domestic portfolio (DP), which combines the risk-free asset and a portfolio of domestic securities found on the efficient frontier. • He or she begins with the risk-free asset (Rf) and moves out along the security market line until reaching portfolio DP. • This portfolio is defined as the optimal domestic portfolio because it moves out into risky space at the steepest slope. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 9

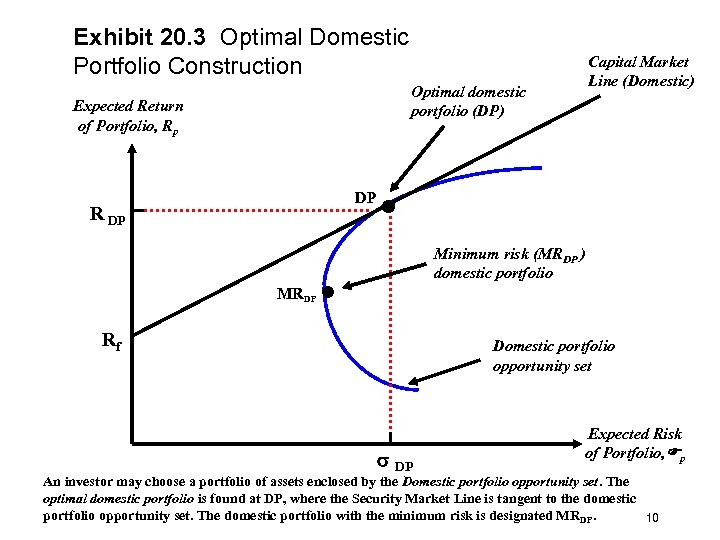Exhibit 20. 3 Optimal Domestic Portfolio Construction Optimal domestic portfolio (DP) Expected Return of Portfolio, Rp DP R DP MRDP Capital Market Line (Domestic) • Minimum risk (MRDP ) domestic portfolio • Rf Domestic portfolio opportunity set DP Expected Risk of Portfolio, p An investor may choose a portfolio of assets enclosed by the Domestic portfolio opportunity set. The optimal domestic portfolio is found at DP, where the Security Market Line is tangent to the domestic portfolio opportunity set. The domestic portfolio with the minimum risk is designated MRDP. 10

International Diversification and Risk • The next exhibit illustrates the impact of allowing the investor to choose among an internationally diversified set of potential portfolios. • The internationally diversified portfolio opportunity set shifts leftward of the purely domestic opportunity set. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 11

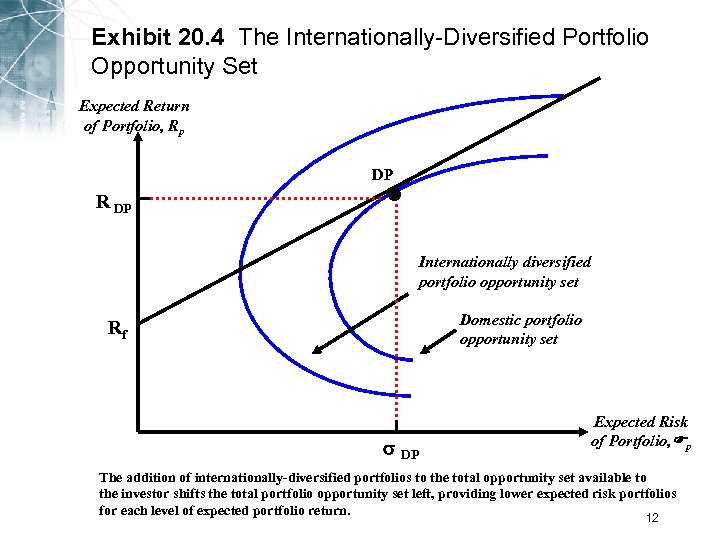Exhibit 20. 4 The Internationally-Diversified Portfolio Opportunity Set Expected Return of Portfolio, Rp • DP R DP Internationally diversified portfolio opportunity set Domestic portfolio opportunity set Rf DP Expected Risk of Portfolio, p The addition of internationally-diversified portfolios to the total opportunity set available to the investor shifts the total portfolio opportunity set left, providing lower expected risk portfolios for each level of expected portfolio return. 12

International Diversification and Risk • It is critical to be clear as to exactly why the internationally diversified portfolio opportunity set is of lower expected risk than comparable domestic portfolios. • The gains arise directly from the introduction of additional securities and/or portfolios that are of less than perfect correlation with the securities and portfolios within the domestic opportunity set. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 13

International Diversification and Risk • The investor can now choose an optimal portfolio that combines the same risk-free asset as before with a portfolio from the efficient frontier of the internationally diversified portfolio opportunity set. • The optimal international portfolio, IP, is again found by locating that point on the capital market line (internationally diversified) which extends from the risk-free asset return of Rf to a point of tangency along the internationally diversified efficient frontier. • The benefits are obvious in that a higher expected portfolio return with a lower portfolio risk can be obtained when compared to the domestic portfolio alone. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 14

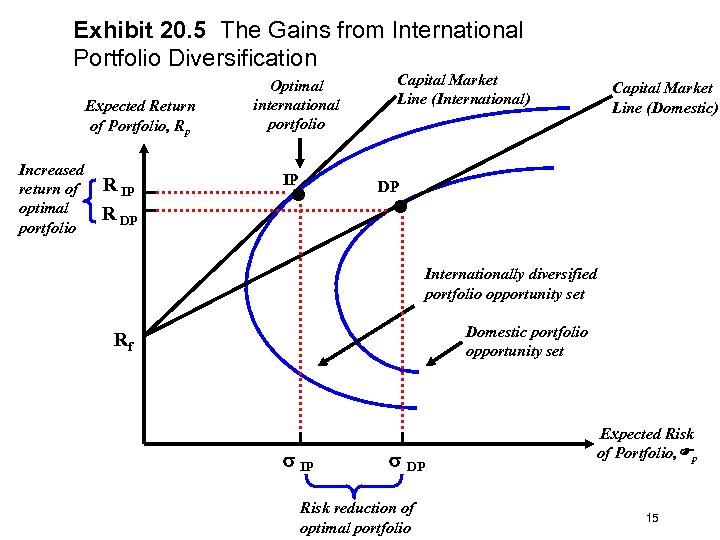Exhibit 20. 5 The Gains from International Portfolio Diversification Expected Return of Portfolio, Rp Increased return of optimal portfolio R IP R DP Optimal international portfolio • IP Capital Market Line (International) Capital Market Line (Domestic) • DP Internationally diversified portfolio opportunity set Domestic portfolio opportunity set Rf IP DP Risk reduction of optimal portfolio Expected Risk of Portfolio, p 15

International Diversification and Risk • An investor can reduce investment risk by holding risky assets in a portfolio. • As long as the asset returns are not perfectly positively correlated, the investor can reduce risk, because some of the fluctuations of the asset returns will offset each other. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 16

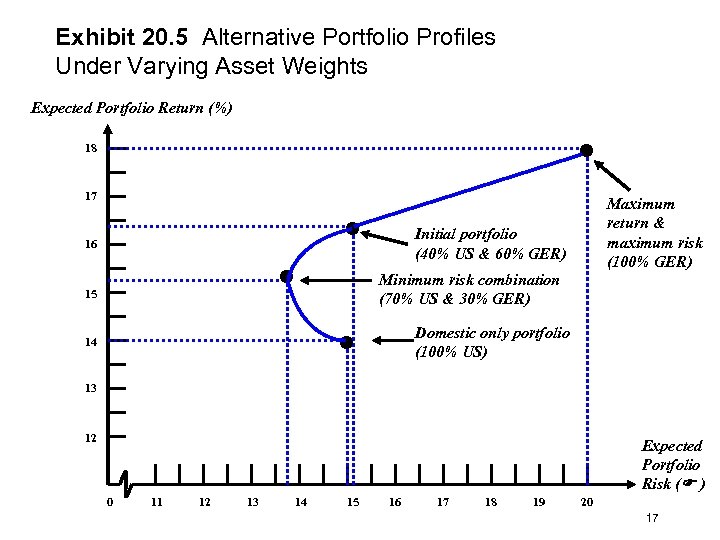Exhibit 20. 5 Alternative Portfolio Profiles Under Varying Asset Weights Expected Portfolio Return (%) • 18 17 16 • 15 • Initial portfolio (40% US & 60% GER) Minimum risk combination (70% US & 30% GER) • 14 Maximum return & maximum risk (100% GER) Domestic only portfolio (100% US) 13 12 Expected Portfolio Risk ( ) 0 11 12 13 14 15 16 17 18 19 20 17

National Markets and Asset Performance • Asset portfolios are traditionally constructed using both interest bearing risk-free assets and risky assets. • For the 100 year period ending in 2000, the risk of investing in equity assets has been rewarded with substantial returns. • The true benefits of global diversification, however, arise from the fact that the returns of different stock markets around the world are not perfectly positively correlated. • This is because the are different industrial structures in different countries, and because different economies do not exactly follow the same business cycle. Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 18

National Markets and Asset Performance • Interestingly, markets that are contiguous or nearcontiguous (geographically) seemingly demonstrate the higher correlation coefficients for the past century. • It is often said that as capital markets around the world become more and more integrated over time, the benefits of diversification will be reduced. • Analysis of market data supports this idea (although the correlation coefficients between markets are still far from 1. 0). Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 19

The International Capital Asset Pricing Model • The use of an international portfolio could have implications on an MNE’s cost of capital. • The capital asset pricing model (CAPM) states that the expected return on an equity by an investor is the sum of two components, a riskfree rate of interest and a risk-premium component (which is based on the perceived riskiness of the individual security relative to the market). Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 20

The International Capital Asset Pricing Model • The CAPM formula is as follows: ke = krf + βi(km – krf) • Where: – ke = expected (required) rate of return on equity i – krf = rate of interest on risk-free bonds (Treasury bonds, for example) – βi = coefficient of systematic risk for the firm – km = expected (required) rate of return on the market portfolio of stocks Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 21

The International Capital Asset Pricing Model • The measure of risk, beta (β), is a measure of how the returns of the individual security, i, are expected to vary and covary with that of the market. • Specifically, beta is calculated as: βi = ρim σi σm Copyright © 2004 Pearson Addison-Wesley. All rights reserved. Where rho (ρim) is the correlation between security i and the market, and σi and σm are the standard deviations of security i and the market, respectively. 22

The International Capital Asset Pricing Model • In theory, the primary distinction in the estimation of the cost of equity for an individual firm using an internationalized version of the CAPM is the definition of the “market” and a recalculation of the firm’s beta for the market. • This is very significant as one must address what sort of portfolio investors hold (domestic or internationally diversified) in determining the expected market return component of the CAPM as well as beta (β). Copyright © 2004 Pearson Addison-Wesley. All rights reserved. 23