Lecture+1.pptx
- Количество слайдов: 130

CHAPTER 2: Number Systems The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3 rd Edition, Irv Englander John Wiley and Sons 2003 Linda Senne, Bentley College Wilson Wong, Bentley College

Why Binary? § Early computer design was decimal § Mark I and ENIAC § John von Neumann proposed binary data processing (1945) § Simplified computer design § Used for both instructions and data § Natural relationship between on/off switches and calculation using Boolean logic Off True False Yes No 1 Chapter 2 Number Systems On 0 2 -2

Counting and Arithmetic § Decimal or base 10 number system § Origin: counting on the fingers § “Digit” from the Latin word digitus meaning “finger” § Base: the number of different digits including zero in the number system § Example: Base 10 has 10 digits, 0 through 9 § § Binary or base 2 Bit (binary digit): 2 digits, 0 and 1 Octal or base 8: 8 digits, 0 through 7 Hexadecimal or base 16: 16 digits, 0 through F § Examples: 1010 = A 16; 1110 = B 16 Chapter 2 Number Systems 2 -3

Keeping Track of the Bits § Bits commonly stored and manipulated in groups § 8 bits = 1 byte § 4 bytes = 1 word (in many systems) § Number of bits used in calculations § Affects accuracy of results § Limits size of numbers manipulated by the computer Chapter 2 Number Systems 2 -4

Numbers: Physical Representation § Different numerals, same number of oranges § Cave dweller: IIIII § Roman: V § Arabic: 5 § Different bases, same number of oranges § 510 § 1012 § 123 Chapter 2 Number Systems 2 -5

Number System § Roman: position independent § Modern: based on positional notation (place value) § Decimal system: system of positional notation based on powers of 10. § Binary system: system of positional notation based powers of 2 § Octal system: system of positional notation based on powers of 8 § Hexadecimal system: system of positional notation based powers of 16 Chapter 2 Number Systems 2 -6
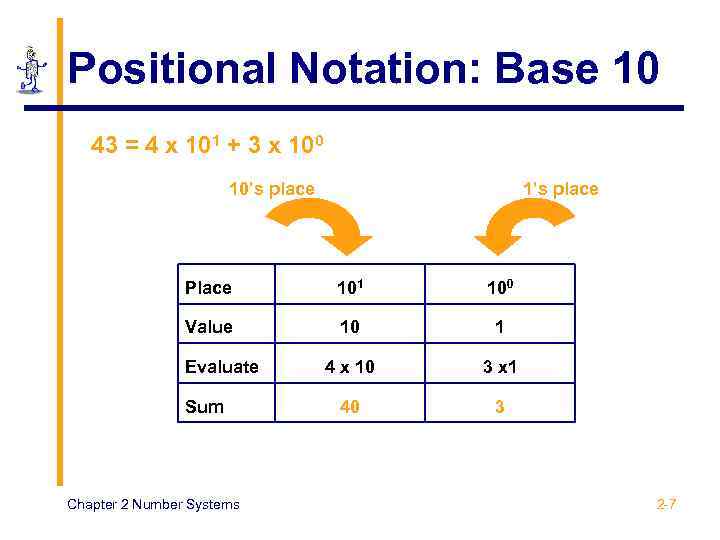
Positional Notation: Base 10 43 = 4 x 101 + 3 x 100 10’s place 1’s place Place 101 100 Value 10 1 4 x 10 3 x 1 40 3 Evaluate Sum Chapter 2 Number Systems 2 -7
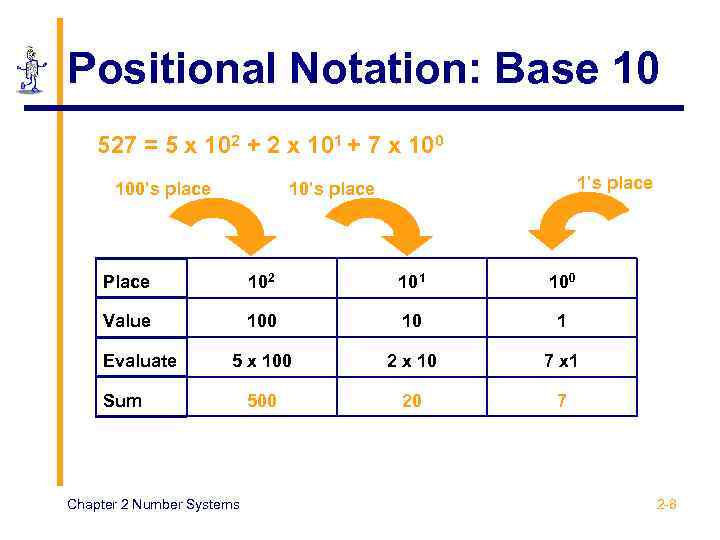
Positional Notation: Base 10 527 = 5 x 102 + 2 x 101 + 7 x 100’s place 10’s place Place 102 101 100 Value 100 10 1 5 x 100 2 x 10 7 x 1 500 20 7 Evaluate Sum Chapter 2 Number Systems 2 -8
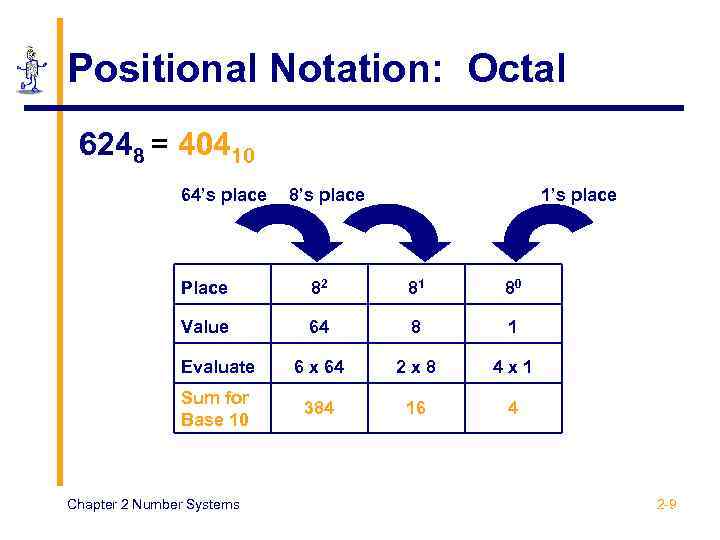
Positional Notation: Octal 6248 = 40410 64’s place 8’s place 1’s place Place 82 81 80 Value 64 8 1 Evaluate 6 x 64 2 x 8 4 x 1 Sum for Base 10 384 16 4 Chapter 2 Number Systems 2 -9
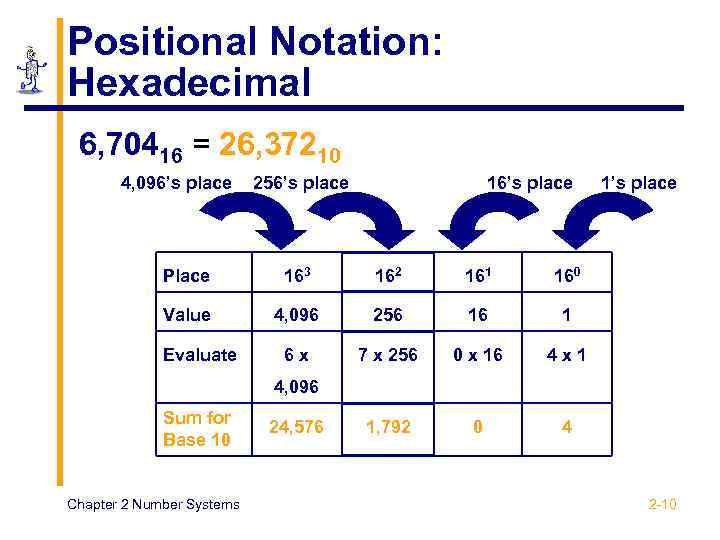
Positional Notation: Hexadecimal 6, 70416 = 26, 37210 4, 096’s place 256’s place 16’s place Place 163 162 161 160 Value 4, 096 256 16 1 6 x 7 x 256 0 x 16 4 x 1 1, 792 0 1’s place 4 Evaluate 4, 096 Sum for Base 10 Chapter 2 Number Systems 24, 576 2 -10
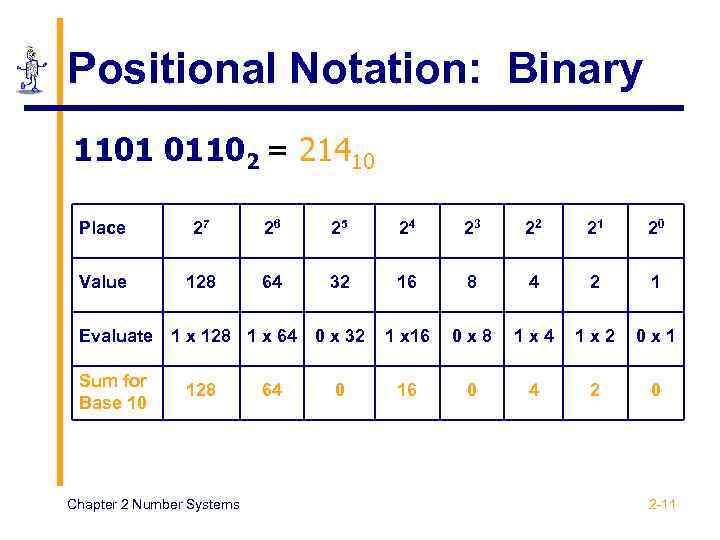
Positional Notation: Binary 1101 01102 = 21410 Place 27 26 25 24 23 22 21 20 Value 128 64 32 16 8 4 2 1 1 x 16 0 x 8 1 x 4 1 x 2 0 x 1 16 0 4 2 0 Evaluate Sum for Base 10 1 x 128 1 x 64 0 x 32 128 Chapter 2 Number Systems 64 0 2 -11
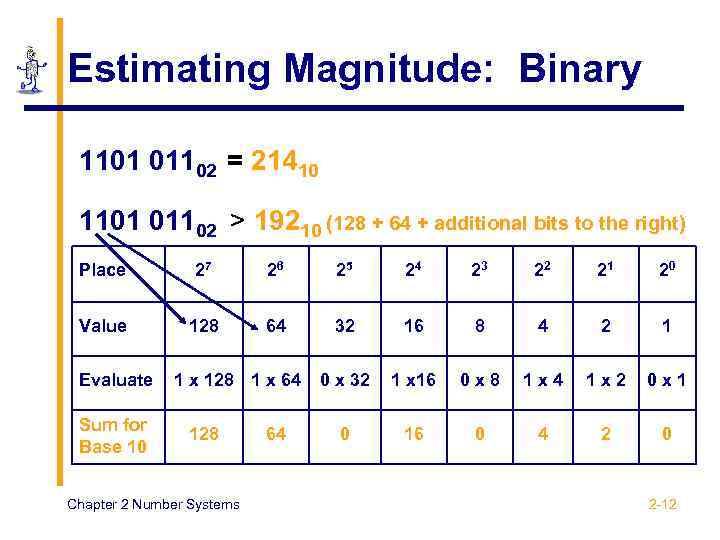
Estimating Magnitude: Binary 1101 01102 = 21410 1101 01102 > 19210 (128 + 64 + additional bits to the right) Place 27 26 25 24 23 22 21 20 Value 128 64 32 16 8 4 2 1 0 x 32 1 x 16 0 x 8 1 x 4 1 x 2 0 x 1 0 16 0 4 2 0 Evaluate Sum for Base 10 1 x 128 1 x 64 128 Chapter 2 Number Systems 64 2 -12

Range of Possible Numbers § R = BK where § R = range § B = base § K = number of digits § Example #1: Base 10, 2 digits § R = 102 = 100 different numbers (0… 99) § Example #2: Base 2, 16 digits § R = 216 = 65, 536 or 64 K § 16 -bit PC can store 65, 536 different number values Chapter 2 Number Systems 2 -13
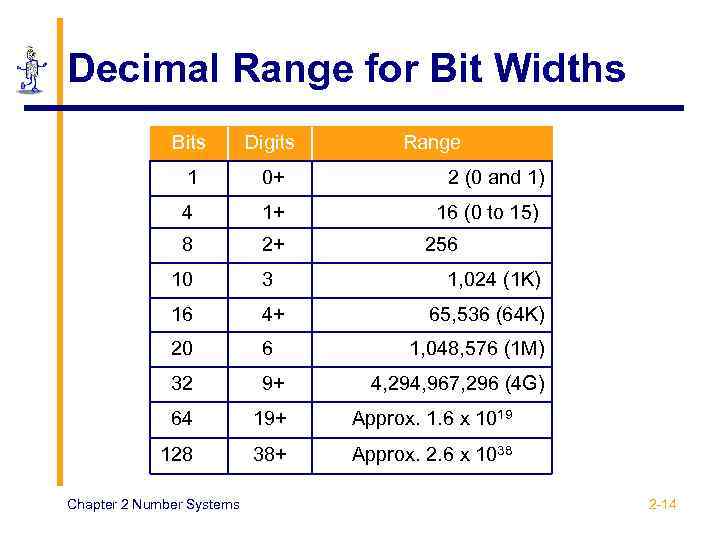
Decimal Range for Bit Widths Bits Digits 1 0+ 4 1+ 8 2+ 10 3 16 4+ 20 6 32 9+ 64 19+ Approx. 1. 6 x 1019 128 38+ Approx. 2. 6 x 1038 Chapter 2 Number Systems Range 2 (0 and 1) 16 (0 to 15) 256 1, 024 (1 K) 65, 536 (64 K) 1, 048, 576 (1 M) 4, 294, 967, 296 (4 G) 2 -14

Base or Radix § Base: § The number of different symbols required to represent any given number § The larger the base, the more numerals are required § § Base 10: Base 2: Base 8: Base 16: Chapter 2 Number Systems 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 2 -15

Number of Symbols vs. Number of Digits § For a given number, the larger the base § the more symbols required § but the fewer digits needed § Example #1: § 6516 10110 1458 110 01012 § Example #2: § 11 C 16 28410 4348 Chapter 2 Number Systems 1 0001 11002 2 -16
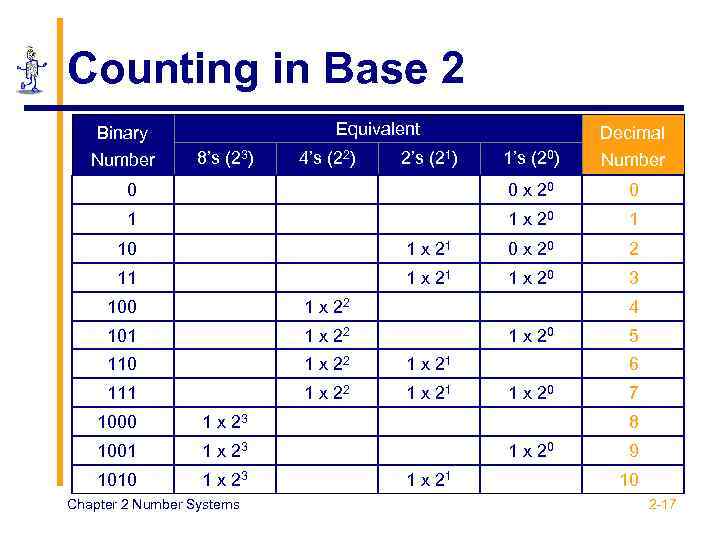
Counting in Base 2 Equivalent Binary 1’s (20) Number 0 0 x 20 0 1 1 x 20 1 Number 8’s (23) 4’s (22) 2’s (21) Decimal 10 1 x 21 0 x 20 2 11 1 x 20 3 100 1 x 22 101 1 x 22 110 1 x 22 1 x 21 111 1 x 22 1 x 21 1000 1 x 23 1010 1 x 23 1 x 20 Chapter 2 Number Systems 5 6 1 x 20 1 x 23 1001 4 7 8 1 x 20 1 x 21 9 10 2 -17
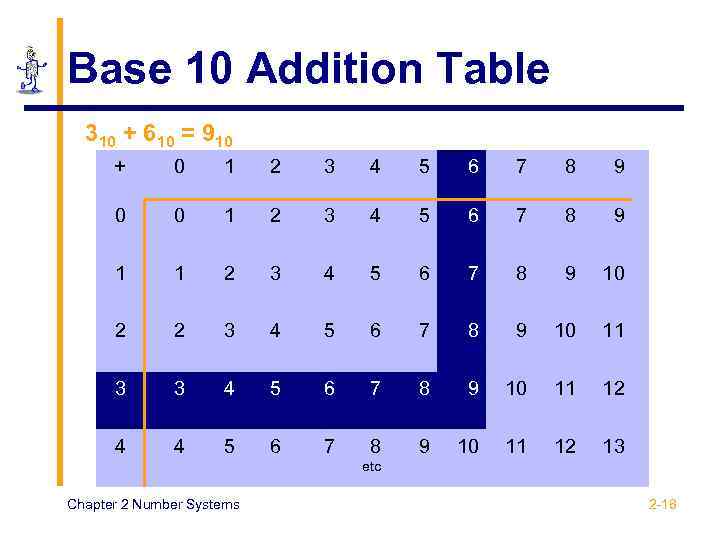
Base 10 Addition Table 310 + 610 = 910 + 0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 10 2 2 3 4 5 6 7 8 9 10 11 3 3 4 5 6 7 8 9 10 11 12 4 4 5 6 7 8 9 10 11 12 13 etc Chapter 2 Number Systems 2 -18
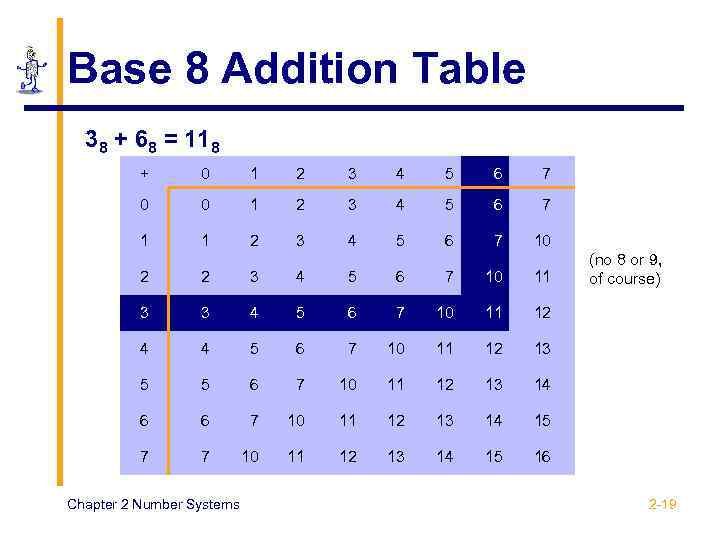
Base 8 Addition Table 38 + 68 = 118 + 0 1 2 3 4 5 6 7 0 0 1 2 3 4 5 6 7 10 2 2 3 4 5 6 7 10 11 3 3 4 5 6 7 10 11 12 4 4 5 6 7 10 11 12 13 5 5 6 7 10 11 12 13 14 6 6 7 10 11 12 13 14 15 7 7 10 11 12 13 14 15 (no 8 or 9, of course) 16 Chapter 2 Number Systems 2 -19
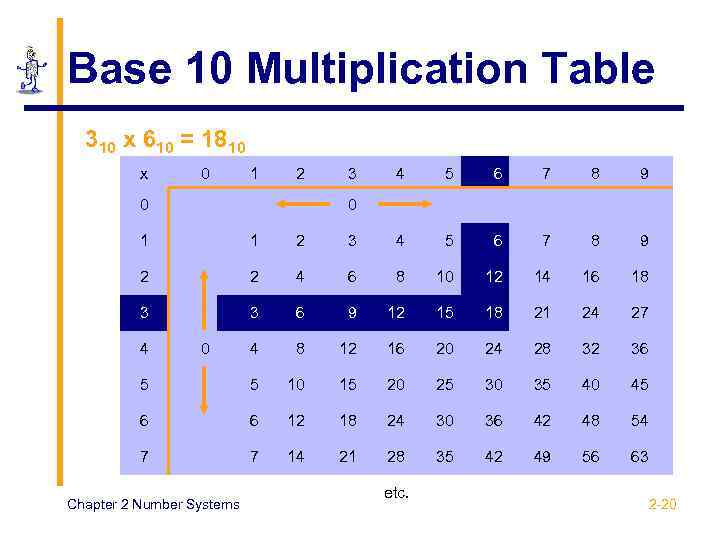
Base 10 Multiplication Table 310 x 610 = 1810 x 0 1 2 0 3 4 5 6 7 8 9 0 1 1 2 3 4 5 6 7 8 9 2 2 4 6 8 10 12 14 16 18 3 3 6 9 12 15 18 21 24 27 4 8 12 16 20 24 28 32 36 5 5 10 15 20 25 30 35 40 45 6 6 12 18 24 30 36 42 48 54 7 7 14 21 28 35 42 49 56 63 4 0 Chapter 2 Number Systems etc. 2 -20
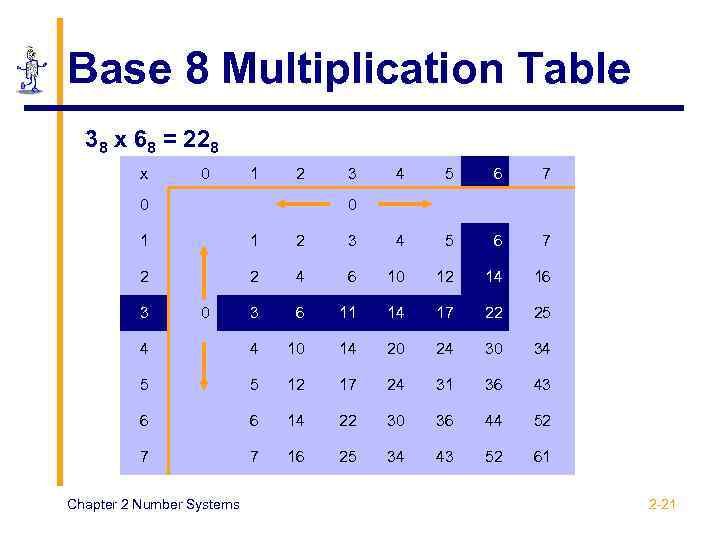
Base 8 Multiplication Table 38 x 68 = 228 x 0 1 2 0 3 4 5 6 7 0 1 1 2 3 4 5 6 7 2 2 4 6 10 12 14 16 3 6 11 14 17 22 25 4 4 10 14 20 24 30 34 5 5 12 17 24 31 36 43 6 6 14 22 30 36 44 52 7 7 16 25 34 43 52 61 3 0 Chapter 2 Number Systems 2 -21
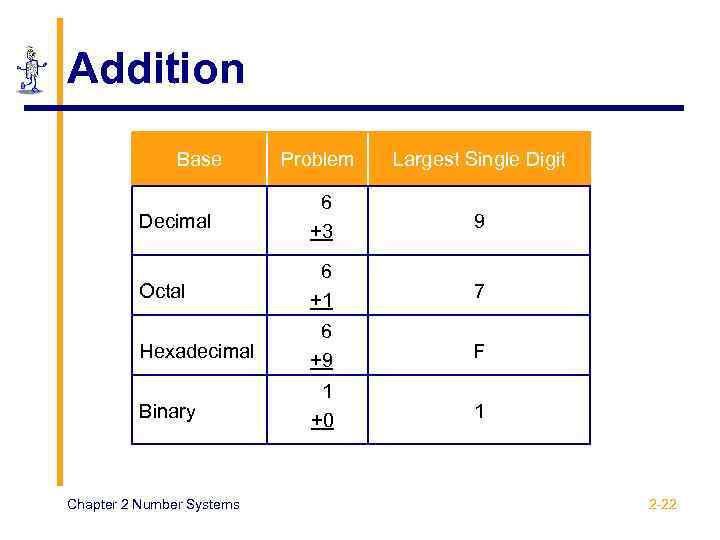
Addition Base Problem Largest Single Digit Decimal 6 +3 9 Octal 6 +1 7 Hexadecimal 6 +9 F Binary 1 +0 1 Chapter 2 Number Systems 2 -22
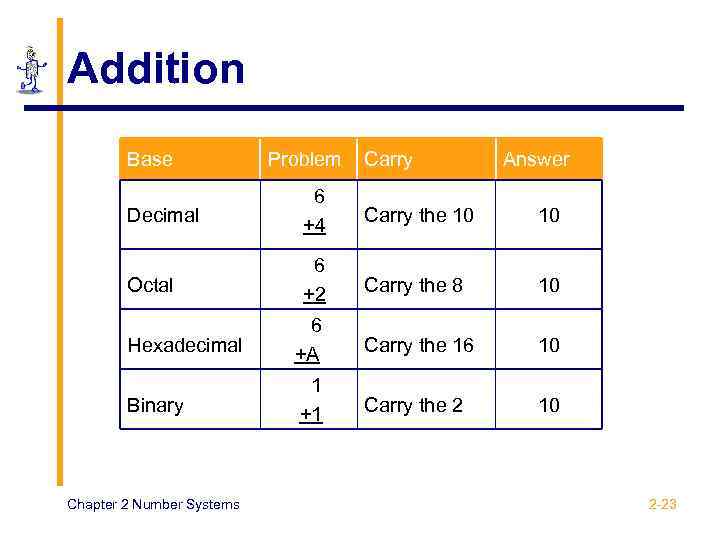
Addition Base Problem Carry Answer Decimal 6 +4 Carry the 10 10 Octal 6 +2 Carry the 8 10 Hexadecimal 6 +A Carry the 16 10 Binary 1 +1 Carry the 2 10 Chapter 2 Number Systems 2 -23

Binary Arithmetic 1 1 1 0 Chapter 2 Number Systems 0 0 1 1 + 1 1 0 0 0 0 1 1 2 -24
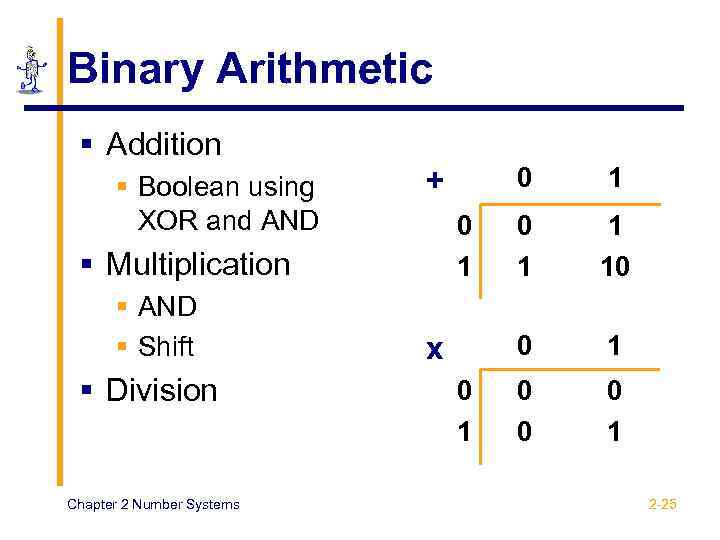
Binary Arithmetic § Addition § Boolean using XOR and AND § Division Chapter 2 Number Systems x 0 1 1 10 0 0 1 § Multiplication § AND § Shift 0 + 1 0 0 0 1 2 -25

Binary Arithmetic: Boolean Logic § Boolean logic without performing arithmetic § EXCLUSIVE-OR p Output is “ 1” only if either input, but not both inputs, is a “ 1” § AND (carry bit) p 1 Output is “ 1” if and only both inputs are a “ 1” 1 1 1 + 1 1 0 0 Chapter 2 Number Systems 1 0 1 1 0 0 1 1 1 0 1 2 -26

Binary Multiplication § Boolean logic without performing arithmetic § AND (carry bit) p Output is “ 1” if and only both inputs are a “ 1” § Shift p p p Shifting a number in any base left one digit multiplies its value by the base Shifting a number in any base right one digit divides its value by the base Examples: p 1010 shift left = 10010 p 1010 shift right = 110 p 102 shift left = 1002 p 102 shift right = 12 Chapter 2 Number Systems 2 -27

Binary Multiplication 1 1 0 1 1’s place 0 2’s place 1 1 1 0 0 4’s place (bits shifted to line up with 4’s place of multiplier) 0 1 0 Chapter 2 Number Systems 1 Result (AND) 2 -28

Binary Multiplication 1 0 1 1 x 1 0 0 1 1 1 0 1 1 1 2’s place (bits shifted to line up with 2’s place of multiplier) 1 0 1 1 0 0 0 1 32’s place 1 0 4’s place 0 1 1 1 0 Result (AND) Note the 0 at the end, since the 1’s place is not brought down. Note: multiple carries are possible. Chapter 2 Number Systems 2 -29
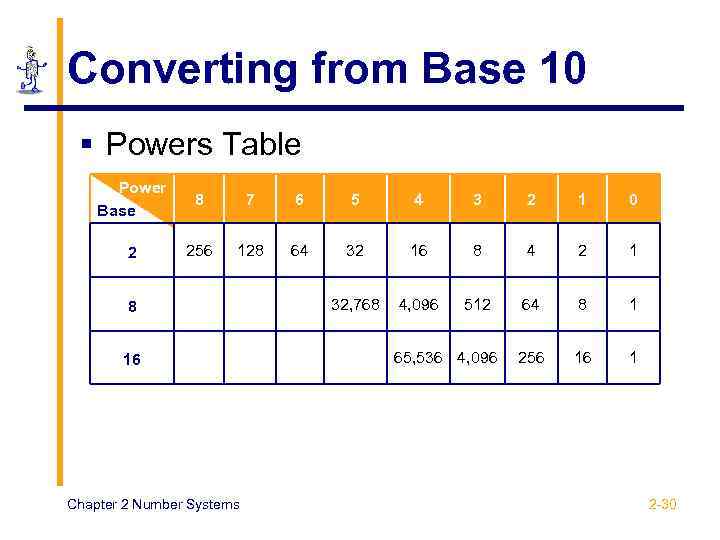
Converting from Base 10 § Powers Table Power Base 8 7 6 5 4 3 2 1 0 2 256 128 64 32 16 8 4 2 1 32, 768 4, 096 512 64 8 1 256 16 1 8 16 Chapter 2 Number Systems 65, 536 4, 096 2 -30
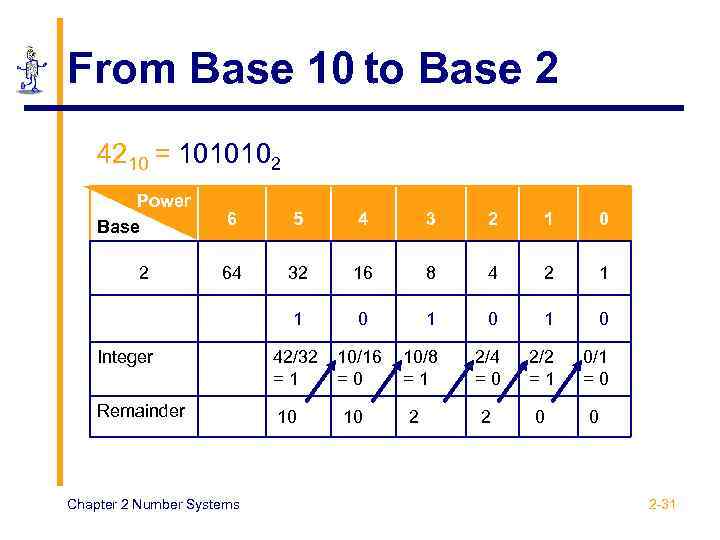
From Base 10 to Base 2 4210 = 1010102 Power Base 6 5 4 3 2 1 0 2 64 32 16 8 4 2 1 1 0 1 0 Integer 42/32 =1 10/16 =0 10/8 =1 2/4 =0 2/2 =1 0/1 =0 Remainder 10 2 0 0 Chapter 2 Number Systems 10 2 2 -31

From Base 10 to Base 2 Base 10 42 Quotient Remainder 2 ) 42 ( 0 Least significant bit 2 ) 21 ( 1 2 ) 10 ( 0 2) 2) 2) Base 2 Chapter 2 Number Systems 5 (1 2 (0 1 Most significant bit 101010 2 -32
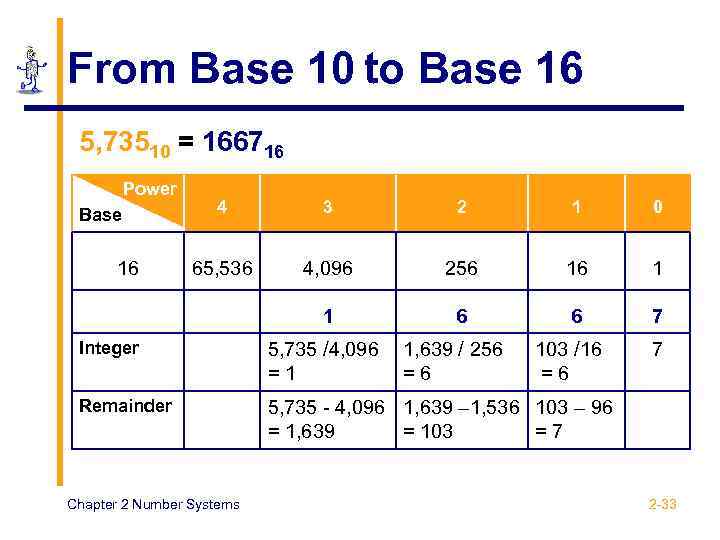
From Base 10 to Base 16 5, 73510 = 166716 Power 16 4 3 2 1 0 65, 536 4, 096 256 16 1 1 Base 6 6 7 Integer 5, 735 /4, 096 =1 Remainder 5, 735 - 4, 096 1, 639 – 1, 536 103 – 96 = 1, 639 = 103 =7 Chapter 2 Number Systems 1, 639 / 256 =6 103 /16 =6 7 2 -33

From Base 10 to Base 16 Base 10 5, 735 Quotient 16 ) 16 ) Base 16 Chapter 2 Number Systems Remainder 5, 735 ( 7 Least significant bit 358 ( 6 22 ( 6 1 ( 1 Most significant bit 0 1667 2 -34

From Base 10 to Base 16 Base 10 8, 039 Quotient 16 ) 16 ) Base 16 Chapter 2 Number Systems Remainder 8, 039 ( 7 Least significant bit 502 ( 6 31 ( 15 1 ( 1 Most significant bit 0 1 F 67 2 -35
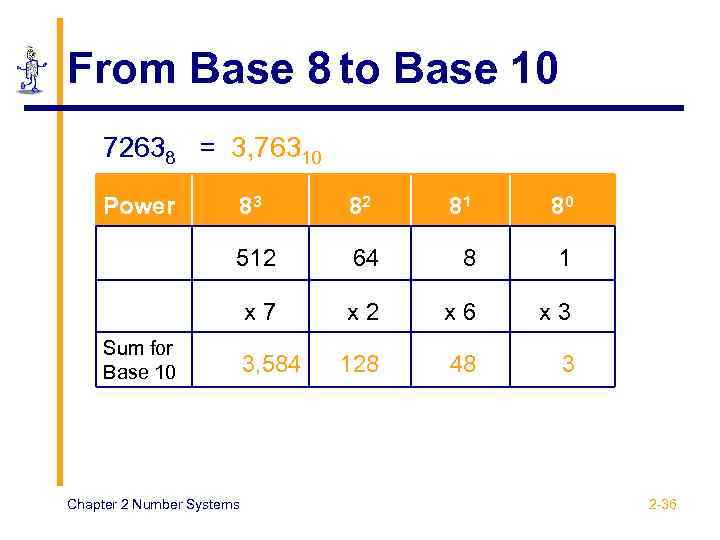
From Base 8 to Base 10 72638 = 3, 76310 Power 83 82 512 x 7 Sum for Base 10 Chapter 2 Number Systems 3, 584 81 80 64 8 1 x 2 x 6 x 3 128 48 3 2 -36

From Base 8 to Base 10 72638 = 3, 76310 7 x 8 56 + 2 = Chapter 2 Number Systems 58 x 8 464 + 6 = 470 x 8 3760 + 3 = 3, 763 2 -37

From Base 16 to Base 2 § The nibble approach § Hex easier to read and write than binary Base 16 1 Base 2 0001 F 6 7 1111 0110 0111 § Why hexadecimal? p Modern computer operating systems and networks present variety of troubleshooting data in hex format Chapter 2 Number Systems 2 -38

Fractions § Number point or radix point § Decimal point in base 10 § Binary point in base 2 § No exact relationship between fractional numbers in different number bases § Exact conversion may be impossible Chapter 2 Number Systems 2 -39

Decimal Fractions § Move the number point one place to the right § Effect: multiplies the number by the base number § Example: 139. 010 139010 § Move the number point one place to the left § Effect: divides the number by the base number § Example: 139. 010 13. 910 Chapter 2 Number Systems 2 -40
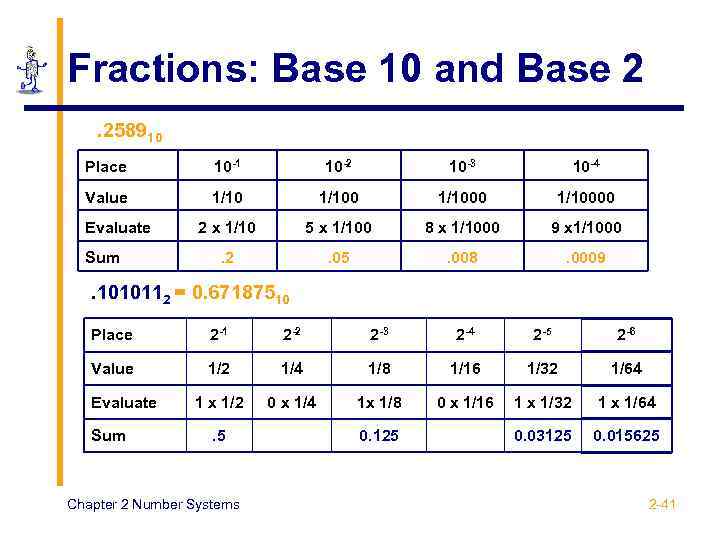
Fractions: Base 10 and Base 2. 258910 Place 10 -1 10 -2 10 -3 10 -4 Value 1/10000 2 x 1/10 5 x 1/100 8 x 1/1000 9 x 1/1000 . 2 . 05 . 008 . 0009 Evaluate Sum . 1010112 = 0. 67187510 Place 2 -1 2 -2 2 -3 2 -4 2 -5 2 -6 Value 1/2 1/4 1/8 1/16 1/32 1/64 1 x 1/2 0 x 1/4 1 x 1/8 0 x 1/16 1 x 1/32 1 x 1/64 0. 03125 0. 015625 Evaluate Sum . 5 Chapter 2 Number Systems 0. 125 2 -41

Fractions: Base 10 and Base 2 § No general relationship between fractions of types 1/10 k and 1/2 k § Therefore a number representable in base 10 may not be representable in base 2 § But: the converse is true: all fractions of the form 1/2 k can be represented in base 10 § Fractional conversions from one base to another are stopped § If there is a rational solution or § When the desired accuracy is attained Chapter 2 Number Systems 2 -42

Mixed Number Conversion § Integer and fraction parts must be converted separately § Radix point: fixed reference for the conversion § Digit to the left is a unit digit in every base § B 0 is always 1 regardless of the base Chapter 2 Number Systems 2 -43

Copyright 2003 John Wiley & Sons All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without express permission of the copyright owner is unlawful. Request for further information should be addressed to the permissions Department, John Wiley & Songs, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages caused by the use of these programs or from the use of the information contained herein. ” Chapter 2 Number Systems 2 -44

The History of Computers

What is a computer? Monitor System Unit Keyboard Floppy Disk Drive CD-ROM / DVD-ROM Drive Mouse §A computer is an electronic machine that accepts information (Data), processes it according to specific instructions, and provides the results as new information.

I- Ancient Counting Machines Ancient Time § 1 - The Abacus (base 5) § (in ancient Babylon, § China, Europe) 2 - The Roman Numerals I II IV V 3 - The Arabic Numerals 0 1 2 3 4 5 VI VIII IX X 7 8 (base 10) 6 9 10

II- Mechanical Counting Machines 1642 § 4 - The Pascaline is a mechanical calculating device invented by the French philosopher and mathematician Blaise

II- Mechanical Counting Machines 1673 § 5 - The Leibniz Wheel was invented by the famous mathematician Leibniz in 1673.

II- Mechanical Counting Machines 1810 § 6 - Punched Cards were used by the French weaver Joseph Jacquard in 1810. The cards carried weaving instructions for

II- Mechanical Counting Machines 1832 § 7 - Babbage’s Difference Engines were calculating machines made by Charles Babbage to produce tables 1852 of numbers that would be used by This device had mechanical problems similar to ship’s navigators. those that plagued Pascal and Leibniz.

The Invention of the Vacuum Tube § 8 - Initially discovered by Thomas Edison, the vacuum tube formed the building block for the entire electronics industry. § *Vacuum tubes were later used as electron valves in the 20 th 1883

III- Electrical Counting Machines 9 - The US census of the 1880 took 9 years to compile and led to inaccurate figures. To solve the problem, Herman Hollerith invented a calculating machine that used electricity §along with punched §cards instead of mechanical gears. 1888

III- Electrical Counting Machines • Hollerith’s machine was immensely successful. The general count of the population, then 63 million, took only 6 1888 weeks to calculate! • Based on the success of his invention, Herman Hollerith and some friends formed a company that sold his invention all over the world. The company eventually became known as:

II- Mechanical Counting Machines 10 - A partial working model of Babbage’s Analytical Engine was completed in 1910 by his son… used punched cards to store numbers. The design was no more successful than its predecessors. 1910

III- Electrical Counting Machines 1943 51 feet long and weighed over 5 tons § 11 - MARK I was built by a team from IBM and Harvard University. Mark I used mechanical telephone switches to store information. It accepted data on punched

IV- Electronic Counting Machines 1946 12 - The ENIAC was the first US-built allelectronic computer built to perform ballistics calculations. (Away from IBM)

IV- Electronic Counting Machines * It was 1000 X faster than Mark I, but it drew a lot of power that dimmed the lights of Philadelphia when it was switched on due to the use of Vacuum Tubes. * Mark I: 5 Additions / sec. * ENIAC: 5, 000 Additions / sec. * ENIAC was made of 18, 000 vacuum tubes. 1946

IV- Electronic Counting Machines ENIAC’s Problems: 1 - short life of vacuum tubes 2 - It runs a single program, which means rewiring by a group of technicians is needed to change the program!!! Solution: the same group of researchers worked on another version of ENIAC that can store programs on punched cards that are much easier to manage and they came up with:

IV- Electronic Counting Machines EDVAC (electronic Discrete Variable Automatic Computer) (was never completed!) 13 - UNIVAC (Universal Automatic Calculator) forty of these computers were sold to businesses. General Electric was the first company to acquire a UNIVAC. * The first UNIVACs were used in the US Army, Air Force, Navy, and Atomic Energy Commission. 1951

The Effect of World War II Back in time to the days of war… * During WWII, the German Navy developed a cipher machine named Enigma. The Enigma machine could automatically encode a message in such a way that only another Enigma machine could read decode it. 1938

The Effect of World War II * In 1938 the Polish Secret Service managed to steal an Enigma machine that was smuggled to England. * Secretly the British developed a computer named Colossus that could decipher as many as 2, 000 messages per day. That computer used Vacuum tubes and was the world’s first entirely digital computer. Surprisingly, though Colossus presented a similar technology to that of ENIAC, it had only 2, 400 compared to 18, 000 in ENIAC!!! 1938

Two Inventions that changed the way computers are built!! 1 - The Transistor The most significant single invention of the modern era. It was invented by 3 scsientists at At&T’s Bell Labs. One of the first overseas companies was a Japanese company called Tokyo Telecommunications Laboratory. The company had troubles paying the license fee ($25, 000) that company became in 1956 what’s called now Sony! it replaced the Vacuum tube. * Transistors are smaller (sometimes microscopic) * Fast and don’t need to warm up 1946

Transistors on a circuit board Resistors Transistors Capacitor
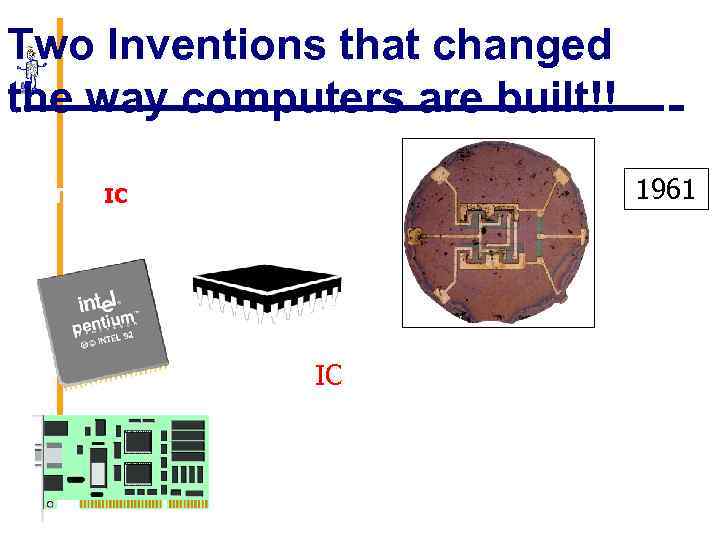
Two Inventions that changed the way computers are built!! 2 - The (IC) Integrated Circuit 1961 The IC revolutionized the entire electronic technology. Ex: The Pentium Processor contains 3. 1 Million Transistors in 1. 5 inch square!
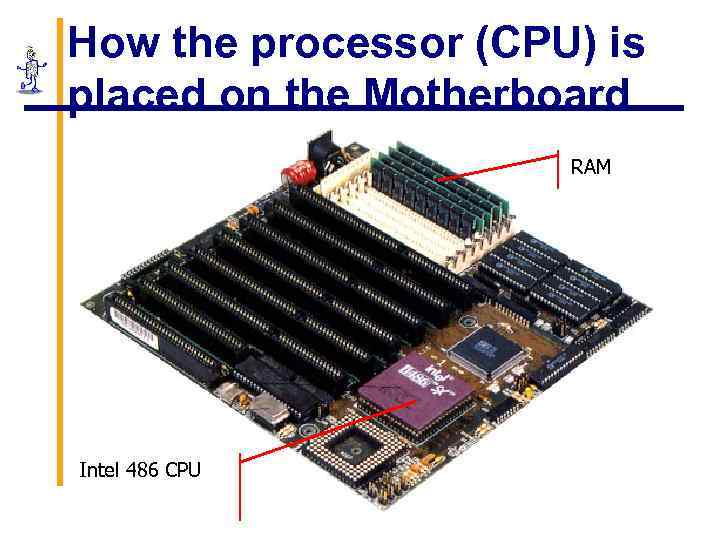
How the processor (CPU) is placed on the Motherboard RAM Intel 486 CPU
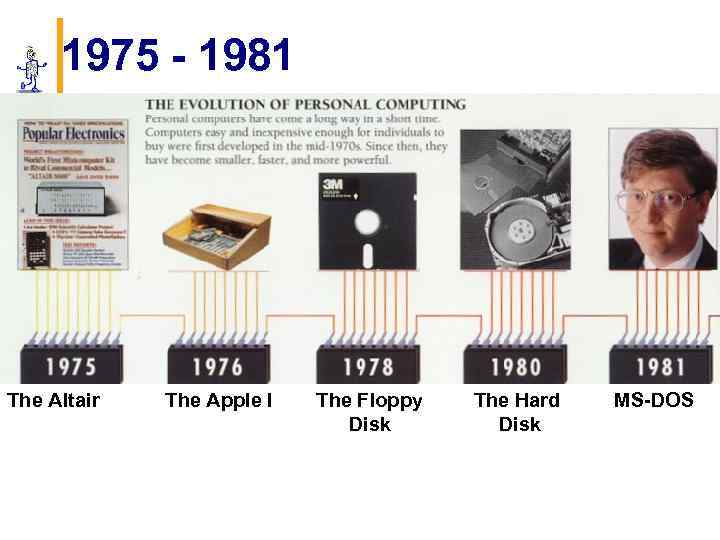
1975 - 1981 The Altair The Apple I The Floppy Disk The Hard Disk MS-DOS
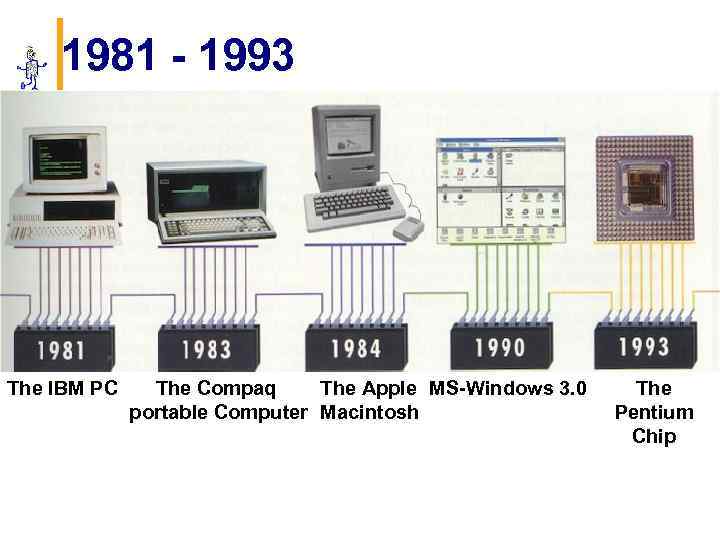
1981 - 1993 The IBM PC The Compaq The Apple MS-Windows 3. 0 portable Computer Macintosh The Pentium Chip

Intel Pentium Processors PENTIUM Pro PENTIUM II

What is a computer? § Simply put, a computer is a sophisticated electronic calculating machine that: § Accepts input information, § Processes the information according to a list of internally stored instructions and § Produces the resulting output information. § Functions performed by a computer are: 70 § Accepting information to be processed as input.
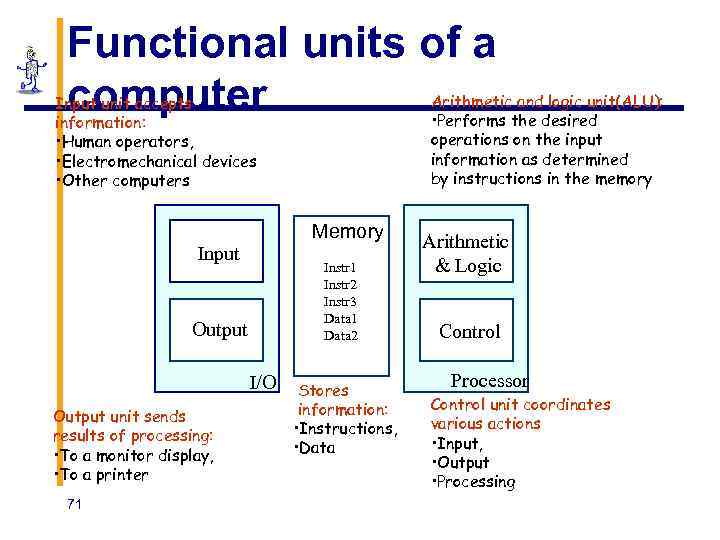
Functional units of a computer Arithmetic and logic unit(ALU): • Performs the desired operations on the input information as determined by instructions in the memory Input unit accepts information: • Human operators, • Electromechanical devices • Other computers Memory Input Instr 1 Instr 2 Instr 3 Data 1 Data 2 Output I/O Output unit sends results of processing: • To a monitor display, • To a printer 71 Stores information: • Instructions, • Data Arithmetic & Logic Control Processor Control unit coordinates various actions • Input, • Output • Processing

Information in a computer -Instructions § Instructions specify commands to: § Transfer information within a computer (e. g. , from memory to ALU) § Transfer of information between the computer and I/O devices (e. g. , from keyboard to computer, or computer to printer) § Perform arithmetic and logic operations (e. g. , Add two numbers, Perform a logical AND). § A sequence of instructions to perform a task is called a program, which is stored in the memory. § Processor fetches instructions that make up a program from the memory 72 and performs the operations stated in

Information in a computer -Data § Data are the “operands” upon which instructions operate. § Data could be: § Numbers, § Encoded characters. § Data, in a broad sense means any digital information. § Computers use data that is encoded as a string of binary digits called bits. 73
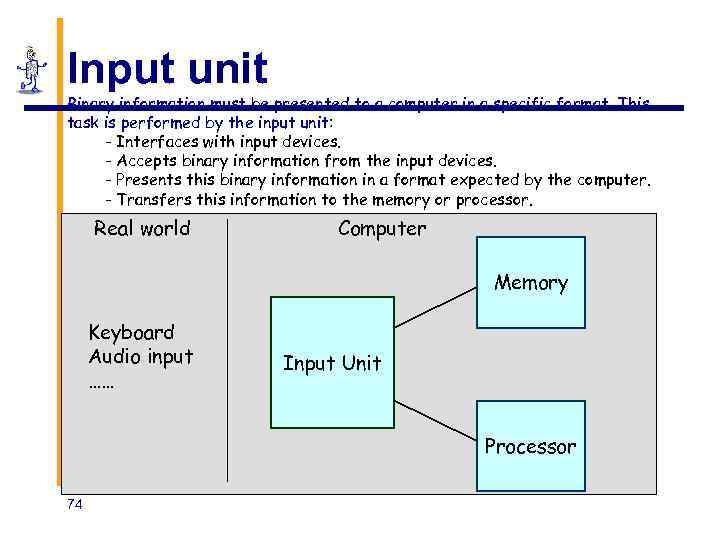
Input unit Binary information must be presented to a computer in a specific format. This task is performed by the input unit: - Interfaces with input devices. - Accepts binary information from the input devices. - Presents this binary information in a format expected by the computer. - Transfers this information to the memory or processor. Real world Computer Memory Keyboard Audio input …… Input Unit Processor 74

Memory unit § Memory unit stores instructions and data. § Recall, data is represented as a series of bits. § To store data, memory unit thus stores bits. § Processor reads instructions and reads/writes data from/to the memory during the execution of a program. § § 75 In theory, instructions and data could be fetched one bit at a time. In practice, a group of bits is fetched at a time. Group of bits stored or retrieved at a time is termed as “word” Number of bits in a word is termed as the “word length” of a computer. § In order to read/write to and from

Memory unit (contd. . ) § Processor reads/writes to/from memory based on the memory address: § Access any word location in a short and fixed amount of time based on the address. § Random Access Memory (RAM) provides fixed access time independent of the location of the word. § Access time is known as “Memory Access Time”. § Memory and processor have to “communicate” with each other in order to read/write information. § In order to reduce “communication time”, a small amount of RAM (known as Cache) is tightly coupled with the processor. § Modern computers have three to four levels of RAM units with different 76 speeds and sizes: § Fastest, smallest known as Cache

Memory unit (contd. . ) § Primary storage of the computer consists of RAM units. § Fastest, smallest unit is Cache. § Slowest, largest unit is Main Memory. § Primary storage is insufficient to store large amounts of data and programs. § Primary storage can be added, but it is expensive. § Store large amounts of data on secondary storage devices: 77 § Magnetic disks and tapes, § Optical disks (CD-ROMS). § Access to the data stored in secondary storage in slower, but take

Arithmetic and logic unit (ALU) § Operations are executed in the Arithmetic and Logic Unit (ALU). § Arithmetic operations such as addition, subtraction. § Logic operations such as comparison of numbers. § In order to execute an instruction, operands need to be brought into the ALU from the memory. § Operands are stored in general purpose registers available in the ALU. § Access times of general purpose registers are faster than the cache. § Results of the operations are stored 78
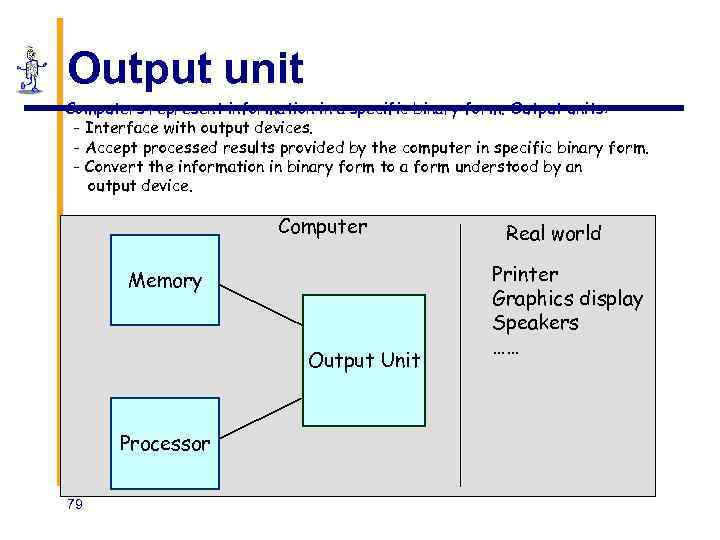
Output unit • Computers represent information in a specific binary form. Output units: - Interface with output devices. - Accept processed results provided by the computer in specific binary form. - Convert the information in binary form to a form understood by an output device. Computer Memory Output Unit Processor 79 Real world Printer Graphics display Speakers ……

Control unit § Operation of a computer can be summarized as: § § Accepts information from the input units (Input unit). Stores the information (Memory). Processes the information (ALU). Provides processed results through the output units (Output unit). § Operations of Input unit, Memory, ALU and Output unit are coordinated by Control unit. § Instructions control “what” operations take place (e. g. data transfer, 80
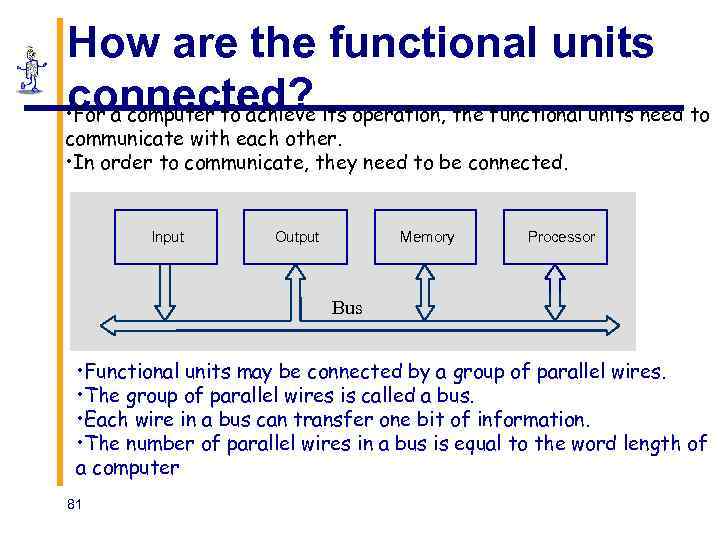
How are the functional units connected? • For a computer to achieve its operation, the functional units need to communicate with each other. • In order to communicate, they need to be connected. Input Output Memory Processor Bus • Functional units may be connected by a group of parallel wires. • The group of parallel wires is called a bus. • Each wire in a bus can transfer one bit of information. • The number of parallel wires in a bus is equal to the word length of a computer 81
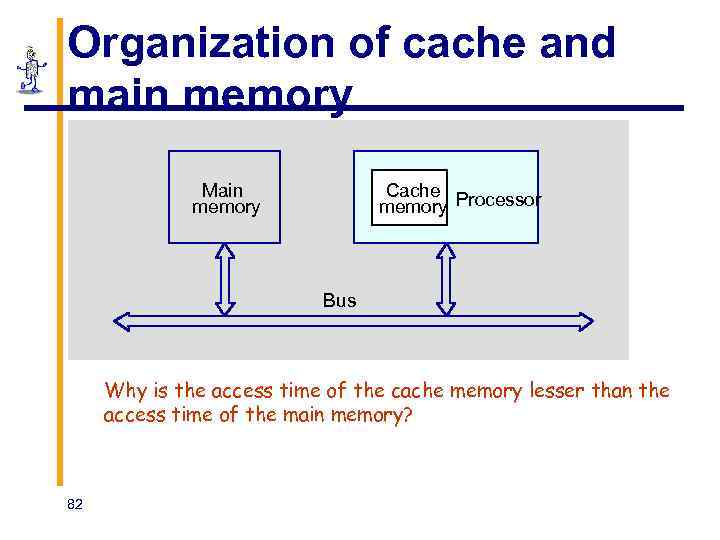
Organization of cache and main memory Main memory Cache memory Processor Bus Why is the access time of the cache memory lesser than the access time of the main memory? 82

Boolean Algebra

LOGIC GATES Formal logic: In formal logic, a statement (proposition) is a declarative sentence that is either true(1) or false (0). It is easier to communicate with computers using formal logic. • Boolean variable: Takes only two values – either true (1) or false (0). They are used as basic units of formal logic.

Boolean function and logic diagram • Boolean function: Mapping from Boolean variables to a Boolean value. • Truth table: § Represents relationship between a Boolean function and its binary variables. § It enumerates all possible combinations of arguments and the corresponding function values.

Boolean function and logic diagram • Boolean algebra: Deals with binary variables and logic operations operating on those variables. • Logic diagram: Composed of graphic symbols for logic gates. A simple circuit sketch that represents inputs and outputs of Boolean functions.
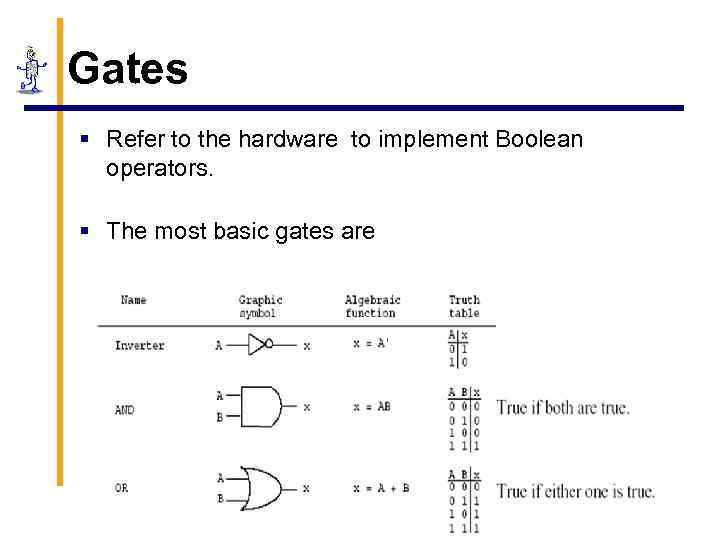
Gates § Refer to the hardware to implement Boolean operators. § The most basic gates are
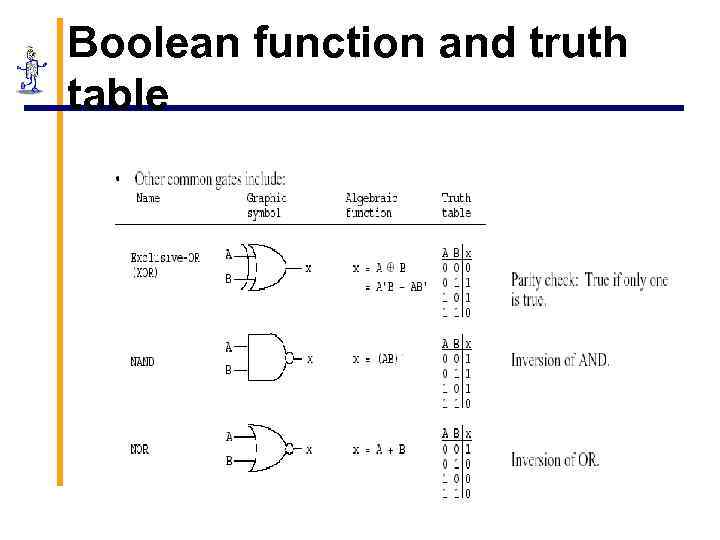
Boolean function and truth table

BASIC IDENTITIES OF BOOLEAN ALGEBRA • Postulate 1 (Definition): A Boolean algebra is a closed algebraic system containing a set K of two or more elements and the two operators · and + which refer to logical AND and logical OR

Basic Identities of Boolean Algebra (Existence of 1 and 0 element) (1) x + 0 = x (2) x · 0 = 0 (3) x + 1 = 1 (4) x · 1 = 1 (Table 1 -1)

Basic Identities of Boolean Algebra (Existence of complement) (5) x + x = x (6) x · x = x (7) x + x’ = x (8) x · x’ = 0

Basic Identities of Boolean Algebra (Commutativity): (9) x + y = y + x (10) xy = yx

Basic Identities of Boolean Algebra (Associativity): (11) x + ( y + z ) = ( x + y ) + z (12) x (yz) = (xy) z

Basic Identities of Boolean Algebra (Distributivity): (13) x ( y + z ) = xy + xz (14) x + yz = ( x + y )( x + z)

Basic Identities of Boolean Algebra (De. Morgan’s Theorem) (15) ( x + y )’ = x’ y’ (16) ( xy )’ = x’ + y’

Basic Identities of Boolean Algebra (Involution) (17) (x’)’ = x

Function Minimization using Boolean Algebra § Examples: (a) a + ab = a(1+b)=a (b) a(a + b) = a. a +ab=a(1+b)=a. (c) a + a'b = (a + a')(a + b)=1(a + b) =a+b (d) a(a' + b) = a. a' +ab=0+ab=ab

Try § F = abc + abc’ + a’c

The other type of question Show that; 1 - ab + ab' = a 2 - (a + b)(a + b') = a 1 - ab + ab' = a(b+b') = a. 1=a 2 - (a + b)(a + b') = a. a +a. b' +a. b+b. b' = a + a. b' +a. b + 0 = a + a. (b' +b) + 0 = a + a. 1 +0 = a +a=a

More Examples § Show that; (a) ab + ab'c = ab + ac (b) (a + b)(a + b' + c) = a + bc (a) ab + ab'c = a(b + b'c) = a((b+b'). (b+c))=a(b+c)=ab+ac (b) (a + b)(a + b' + c) = (a. a + a. b' + a. c + ab +b. b' +bc) =…

De. Morgan's Theorem (a) (a + b)' = a'b' (b) (ab)' = a' + b' Generalized De. Morgan's Theorem (a) (a + b + … z)' = a'b' … z' (b) (a. b … z)' = a' + b' + … z‘

De. Morgan's Theorem § F = ab + c’d’ § F’ = ? ? § F = ab + c’d’ + b’d § F’ = ? ?

De. Morgan's Theorem Show that: (a + b. c)' = a'. b' + a'. c'

More De. Morgan's example Show that: (a(b + z(x + a')))' =a' + b' (z' + x') (a(b + z(x + a')))' = a' + (b + z(x + a'))' = a' + b' (z' + (x + a')') = a' + b' (z' + x'(a')') = a' + b' (z' + x'a) =a‘+b' z' + b'x'a =(a‘+ b'x'a) + b' z' =(a‘+ b'x‘)(a +a‘) + b' z' = a‘+ b'x‘+ b' z‘ = a' + b' (z' + x')

More Examples (a(b + c) + a'b)'=b'(a' + c') ab + a'c + bc = ab + a'c (a + b)(a' + c)(b + c) = (a + b)(a' + c)

Chapter 10 Operating Systems 106

Chapter Goals § § § Describe the two main responsibilities of an operating system Define memory and process management Explain how timesharing creates the virtual machine illusion Explain the relationship between logical and physical addresses Compare and contrast memory management techniques 107

Software Categories Application software Software written to address specific needs—to solve problems in the real world Word processing programs, games, inventory control systems, automobile diagnostic programs, and missile guidance programs are all application software System software Software that manages a computer system at a fundamental level It provides the tools and an environment in which application software can be created and run 108

Operating System § An operating system § § § manages computer resources, such as memory and input/output devices provides an interface through which a human can interact with the computer allows an application program to interact with these other system resources 109
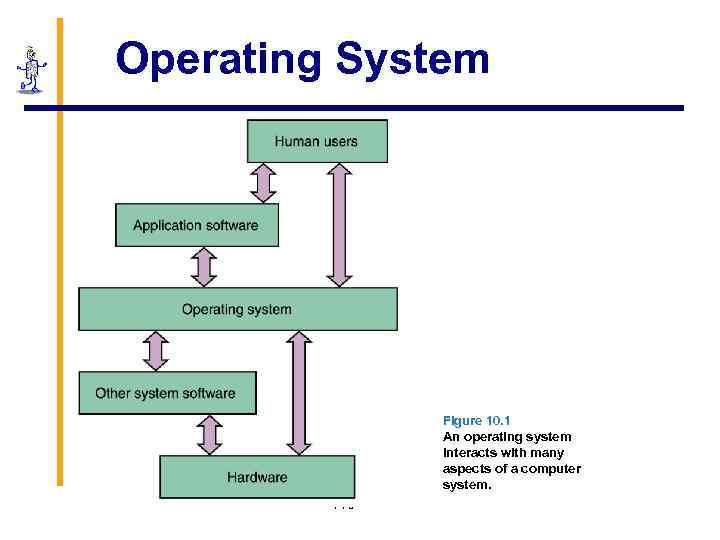
Operating System Figure 10. 1 An operating system interacts with many aspects of a computer system. 110

Operating System § The various roles of an operating system generally revolve around the idea of “sharing nicely” § An operating system manages resources, and these resources are often shared in one way or another among programs that want to use them 111

Resource Management Multiprogramming The technique of keeping multiple programs in main memory at the same time that compete for access to the CPU so that they can execute Memory management The process of keeping track of what programs are in memory and where in memory they reside 112

Resource Management Process A program in execution § The operating system performs process management to carefully track the progress of a process and all of its intermediate states CPU scheduling determines which process in memory is executed by the CPU at any given point 113

Batch Processing § A typical computer in the 1960 s and ‘ 70 s was a large machine § Its processing was managed by a human operator § The operator would organize various jobs from multiple users into batches 114
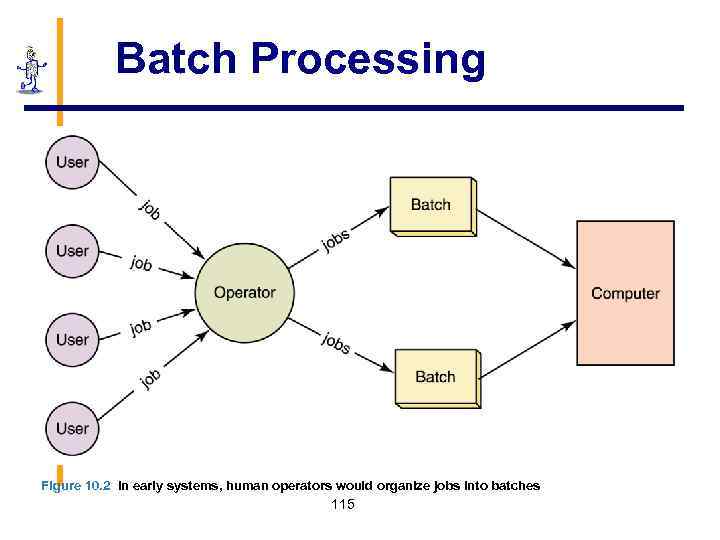
Batch Processing Figure 10. 2 In early systems, human operators would organize jobs into batches 115

Timesharing system A system that allows multiple users to interact with a computer at the same time Multiprogramming A technique that allows multiple processes to be active at once, allowing programmers to interact with the computer system directly, while still sharing its resources § In a timesharing system, each user has his or her own virtual machine, in which all system resources are (in effect) available for use 116

Other Factors Real-time System A system in which response time is crucial given the nature of the application Response time The time delay between receiving a stimulus and producing a response Device driver A small program that “knows” the way a particular device expects to receive and deliver information. 117

Memory Management § Operating systems must employ techniques to § Track where and how a program resides in memory § Convert logical addresses into actual addresses Logical address (sometimes called a virtual or relative address) A value that specifies a generic location, relative to the program but not to the reality of main memory Physical address An actual address in the main memory device 118
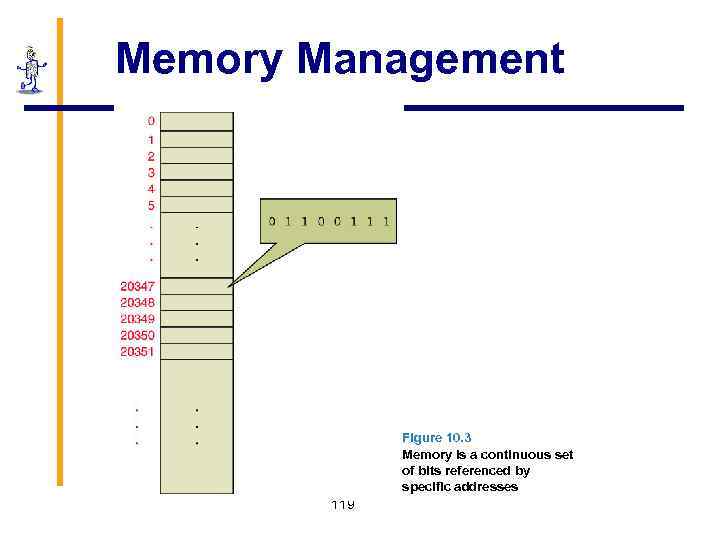
Memory Management Figure 10. 3 Memory is a continuous set of bits referenced by specific addresses 119
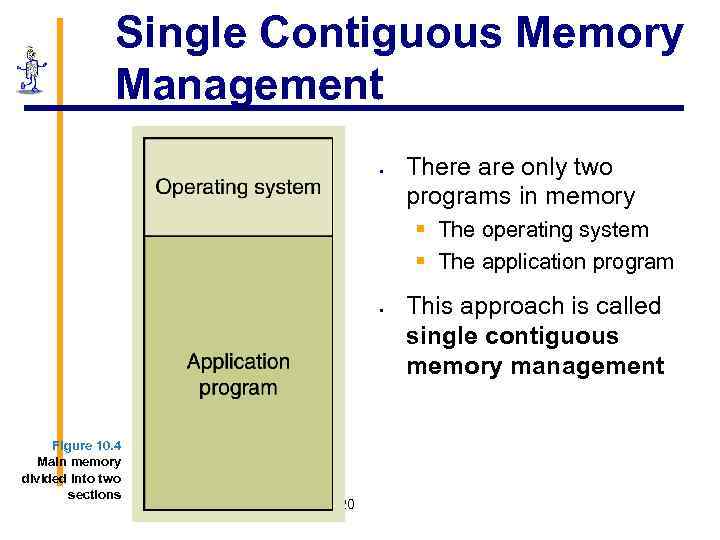
Single Contiguous Memory Management § There are only two programs in memory § The operating system § The application program § Figure 10. 4 Main memory divided into two sections 120 This approach is called single contiguous memory management

Single Contiguous Memory Management § A logical address is simply an integer value relative to the starting point of the program § To produce a physical address, we add a logical address to the starting address of the program in physical main memory 121
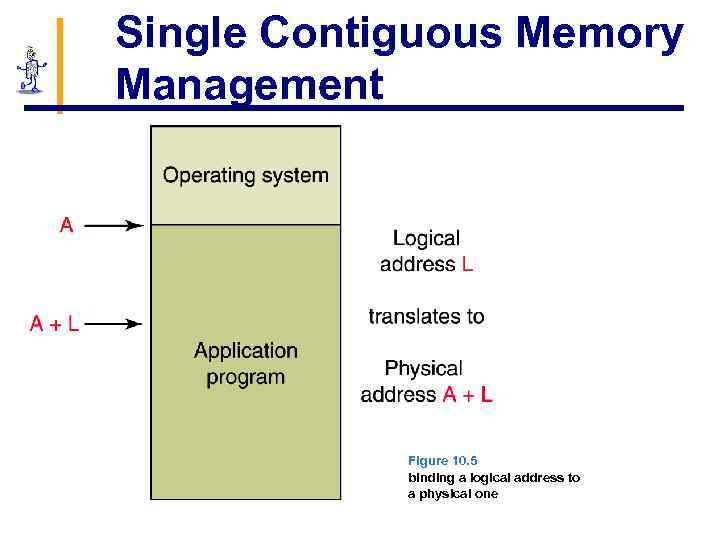
Single Contiguous Memory Management 122 Figure 10. 5 binding a logical address to a physical one

Partition Memory Management Fixed partitions Main memory is divided into a particular number of partitions Dynamic partitions Partitions are created to fit the needs of the programs 123

Partition Memory Management § At any point in time memory is divided into a set of partitions, some empty and some allocated to programs Base register A register that holds the beginning address of the current partition Bounds register A register that holds the length of the current partition Figure 10. 6 Address resolution in partition memory management 124

Partition Selection Algorithms Which partition should we allocate to a new program? • • • First fit Allocate program to the first partition big enough to hold it Best fit Allocated program to the smallest partition big enough to hold it Worst fit Allocate program to the largest partition big enough to hold it 125

Paged Memory Management Paged memory technique A memory management technique in which processes are divided into fixed-size pages and stored in memory frames when loaded into memory Frame A fixed-size portion of main memory that holds a process page Page A fixed-size portion of a process that is stored into a memory frame Page-map table (PMT) A table used by the operating system to keep track of page/frame relationships 126

Paged Memory Management § § Figure 10. 7 A paged memory management approach 127 To produce a physical address, you first look up the page in the PMT to find the frame number in which it is stored Then multiply the frame number by the frame size and add the offset to get the physical address

Paged Memory Management Demand paging An important extension of paged memory management § § Not all parts of a program actually have to be in memory at the same time In demand paging, the pages are brought into memory on demand Page swap The act of bringing in a page from secondary memory, which often causes another page to be written back to secondary memory 128

Paged Memory Management § The demand paging approach gives rise to the idea of virtual memory, the illusion that there are no restrictions on the size of a program § Too much page swapping, however, is called thrashing and can seriously degrade system performance. 129

Have A Good Night Autumn Moon by Ansel Adams Nasa Encore 130
Lecture+1.pptx