Chapter 2 Mechanics of Materials Tensile stress

Chapter 2 Mechanics of Materials Tensile stress (+) A Compressive stress (-) Normal stress = At a point: Example: Estimate the normal stress on a shin bone (脛骨) 1 Jump to first page

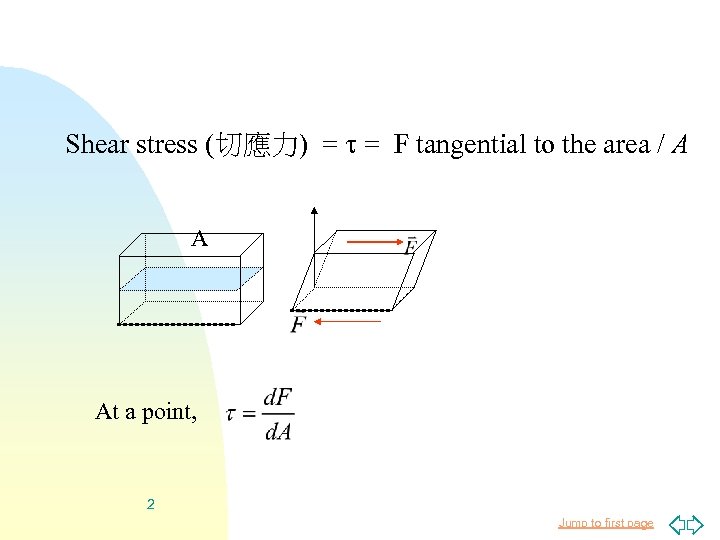Shear stress (切應力) = = F tangential to the area / A A At a point, 2 Jump to first page

Normal strain (正應變) = fractional change of length= x l Shear strain (? ) = deformation under shear stress = x F fixed F 3 Jump to first page

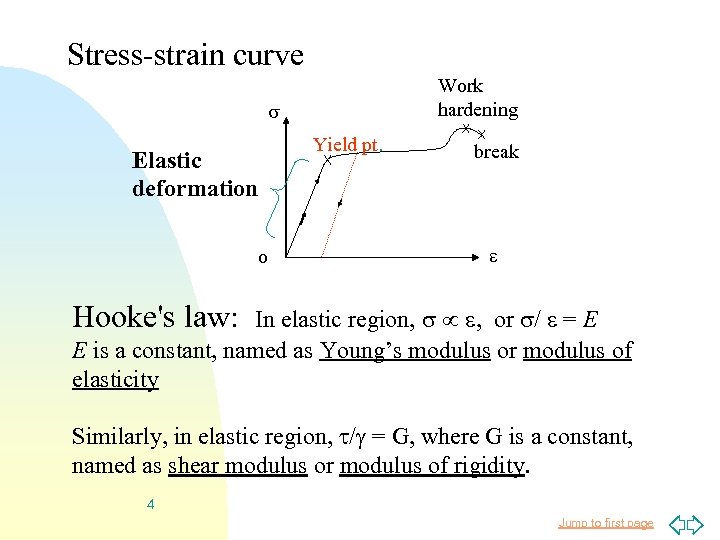Stress-strain curve Work hardening Elastic deformation o Yield pt. break Hooke's law: In elastic region, , or / = E E is a constant, named as Young’s modulus or modulus of elasticity Similarly, in elastic region, / = G, where G is a constant, named as shear modulus of rigidity. 4 Jump to first page

Exercise set 2 (Problem 3) Find the total extension of the bar. o dx 15 mm W 0. 6 m X 1. 2 m Width of a cross-sectional element at x: Stress in this element : Strain of this element: The extension of this element : The total extension of the whole bar is : = 2. 13 x 10 -4 m 5 Jump to first page

Bulk modulus 6 Jump to first page

Poisson's ratio : For a homogeneous isotropic material d F F x n n normal strain : lateral strain : Poisson's ratio : value of : 0. 2 - 0. 5 7 Jump to first page

Double index notation for stress and strain 1 st index: surface, 2 nd index: force For normal stress components : x xx, y yy , z zz, x xx z zx xz zy xy yz yx y 8 Jump to first page

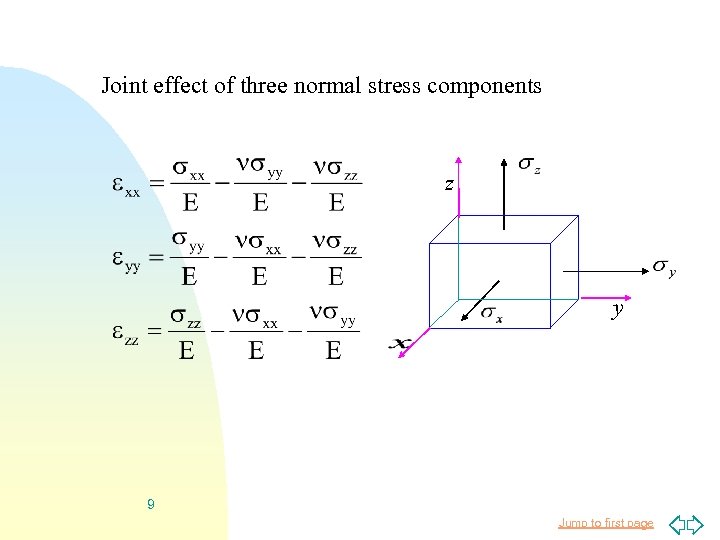Joint effect of three normal stress components z y 9 Jump to first page

Symmetry of shear stress components Take moment about the z axis, total torque = 0, ( xy y z) x = ( yx x z) y, hence, xy = yx. Similarly, yz = zy and xz = zx y yx xy y z x z x 10 Jump to first page

Original shear strain is “simple” strain = There is no real deformation during pure rotation, but “simple” strain 0. 2 Define pure rotation angle rot and pure shear strain, such that the angular displacements of the two surfaces are: 1= rot+ def and 2= rot- def. Hence, rot = ( 1+ 2)/2 and def = ( 1 - 2)/2 Example: 1 = 0 and 2 = - , so def = (0+ )/2 = /2 and rot= (0 - )/2 = - /2 Pure shear strain is /2 x rot dy def 2 = - x 11 Jump to first page

Example: Show that Proof: For hydrostatic pressure l l l xx = yy = zz = , hence 3 = xx+ yy+ zz = (1 -2 v)( xx+ yy+ zz)/E xx = yy = zz = - p (compressive stress) 12 Jump to first page

Example : Show that nn = /2 Point C moves further along x- and y-direction by distances of AD( /2) and AD( /2) respectively. nn = [(AD /2)2 + (AD /2)2]1/2 / [(AD)2 + (AD)2]1/2 = /2 True shear strain: yx = /2 Therefore, the normal component of strain is equal to the shear component of strain: C’ nn = yx and nn = /2 C D’ A D 13 Jump to first page

Example : Show that nn = nn/(2 G) Consider equilibrium along n-direction: yx (l. W) sin 45 o x 2 = 2 (l cos 45 o) W nn yx l xy 2 lc os o 45 n l Therefore yx = nn From definition : = xy /G = nn /G = 2 nn 14 Jump to first page

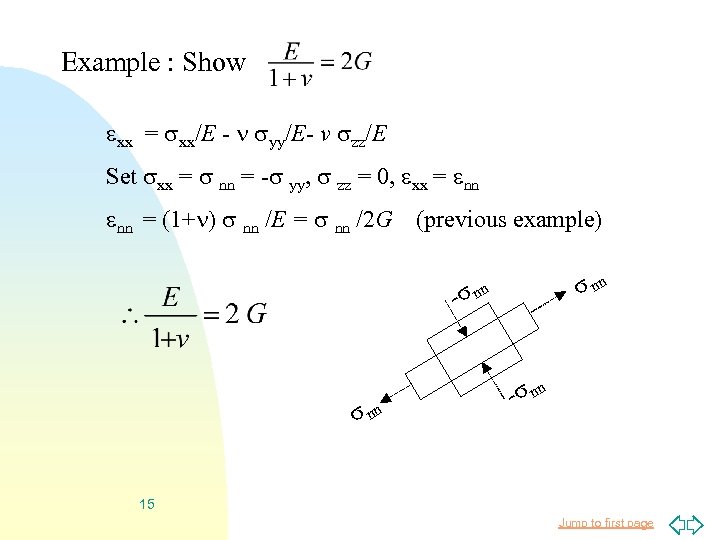Example : Show xx = xx/E - yy/E- v zz/E Set xx = nn = - yy, zz = 0, xx = nn nn = (1+ ) nn /E = nn /2 G (previous example) nn - nn 15 Jump to first page

Ex. 12 k. N forces are applied to the top & bottom of a cube (20 mm edges), E = 60 GPa, = 0. 3. Find (i) the force exerted by the walls, (ii) yy z y 12 k. N x (i) xx = 0, yy = 0 and zz= -12 103 N/(20 10 -3 m)2 = 3 107 Pa xx = ( xx- v yy- v zz) /E 0 = [ xx- 0 – 0. 3 (- 3 107)]/60 109 xx = -9 106 Pa (compressive) Force = A xx = (20 10 -3 m)2 (-9 106 Pa) = -3. 6 103 N (ii) yy = ( yy- v zz- v xx) /E = [0 – 0. 3 (- 3 107) – 0. 3 (- 9 106)]/60 109 = 1. 95 10 -4 16 Jump to first page

Elastic Strain Energy F The F energy stored in a small volume: The energy stored : e=extension x F Energy density in the material : 17 Jump to first page

Similarly for shear strain : F 18 Jump to first page