Chapter 2 Measuring Returns and Risk Measures

Chapter 2 Measuring Returns and Risk

Measures of Investment Returns • Holding Period Return (HPR) and Return Relative (HPRR) • Per-Period Return (PPR) and Return Relative (PPRR) • Compounding • Expected Return • Annualized Return • Geometric Mean (GMR) and Arithmetic Mean Returns

Ex Ante Returns • Returns that are derived from a probability distribution Ex Post Returns • Returns that come from a time series of historical data

Components of Return • Periodic payments: dividends, interest, rents, or royalties • Changes in market value: price appreciation or decline

Holding Period Return (HPR) • Rate of return for the period held Holding Period Return Relative (HPRR) • End-period value relative to beginning-of-period value for specific holding period • holding period return plus one (1)

HPR = (Income Received + Change in Value) Beginning Value HPRR = (Income Received + Ending Value) Beginning Value HPR = HPRR – 1 or 1 + HPR = HPRR

Per-Period Return (PPR) • Return earned for particular period (for example, annual return) Per-Period Return = (Period’s Income + Price Change) Beginning Period Value Per-Period Return Relative (PPRR) Per-Period Return Relative= (Period’s Income + End of Period Value) Beginning Period Value

Impact of Compounding Ending Value = Beginning Value x (1 + rate of return)t where t = the number of time periods Example: beginning value = $100 rate of return = 10% t = 10 years Ending Value = $100 x (1+. 10) 10 = $259. 37

Annualized Rate of Return • Converting Returns for time periods other than one year into annualized returns Rear = (1 + HPR)# where Rear = effective annual interest rate HPR = holding period rate of return # = adjustment factor determined by whether holding period is measured in days, weeks, months, quarters, etc.

Expected Return • Probability Distribution • E(return)=P 1 x. R 1 + P 2 x. R 2 + … + Pnx. Rn

A Portfolio’s Expected Rate of Return • Same formula as HPR for security, or • Weighted average rate of return = W 1 x E(R 1) + W 2 x E(R 2) +. . . + Wn x E(Rn) where Wi = % of portfolio invested in security i, E(Ri) = the per-period return on security i, and W 1 + … + Wn = 1

Geometric Mean Return • Value of compounded per-period average rate of return of financial asset determined during specified time HPRR = PPRR 1 x PPRR 2 x …x PPRRn GMR = HPRR(1 n) – 1

Arithmetic Mean Return • Simple average return found by dividing sum of separate per-period returns by number of periods over which they were earned

Why Arithmetic Mean Is a Really Bad Measure of Returns Over Time R 1 = 100% R 2 = – 50% Arithmetic average return = +25% Geometric mean return = 0%

Relationship between GM and Arithmetic Mean Returns 1. Only when all PPRs are identical will GMR and arithmetic mean be equal 2. If PPRs are not identical, then GMR will always be less than arithmetic mean return 3. Difference increases as variability among PPRs increases

Predicting Future Performance Based on Past Performance • If predicting one period in future, use arithmetic mean • If predicting n periods in future, where n = number of historical periods, use GMR

Risk • Pure Risk versus Speculative Risk • Types of Risk – Purchasing power (or inflation) risk – Interest rate risk – Market risk – Business (and default) risk – Liquidity risk – Political (sovereign) risk – Exchange rate risk – Tax risk – Additional commitment Risk

Pure Risk • Involves only chance of loss but no chance of gain Speculative Risk • Associated with speculation in which there is some chance of gain and some chance of loss

Purchasing Power Risk • Loss of purchasing power of investment asset’s future cash flows 1 + real rate = (1 + nominal rate) (1 + inflation rate) real rate ~ nominal rate – inflation rate

Interest Rate Risk • for debt securities, risk associated with changes in interest rates; consists of price risk and reinvestment rate risk Price Risk • a change in market interest rates produces an opposite change in the value of investments Reinvestment Rate Risk • risk as to what interest rate will be when income and/or principal from investments are reinvested

Market Risk • Degree to which asset’s return is affected by events affecting entire market • Also called systematic risk • Risk that is nondiversifiable

Business Risk • Unique for each enterprise • Also called nonsystematic risk • Risk that can be reduced or eliminated through diversification

Default Risk • Risk that contractual payments will not be honored

Financial Risk • Risk that companies with heavy use of debt financing will have more volatile rates of return

Liquidity Risk • Relative inability to convert an asset to cash quickly, at any time, and without any loss of principal

Political (Sovereign) Risk • Degree to which investment asset subject to events in foreign markets that can cause the value of these investments to drop precipitously • Includes: – effects of trade disputes – wars – political unrest – tariffs – corruption – expropriation

Exchange Rate Risk • Degree to which investment asset affected by movements in currency exchange rates in country where investment is located • Affects investments in some U. S. companies because of overseas markets, production facilities, and raw materials

Tax Risk • Extent to which investment’s returns are exposed to changes in tax laws • Income that is not currently taxable may be taxable later

Investment Manager Risk • Risk that managed fund will perform below average due to poor investment decisions • Can minimize risk through diversification or use of index funds

Additional Commitment Risk • Degree to which investment asset may require the buyer to put additional money into that investment • Inability to meet commitment might create loss of value

Measures of Risk • Range • Semivariance • Standard Deviation • Coefficient of Variation • Beta

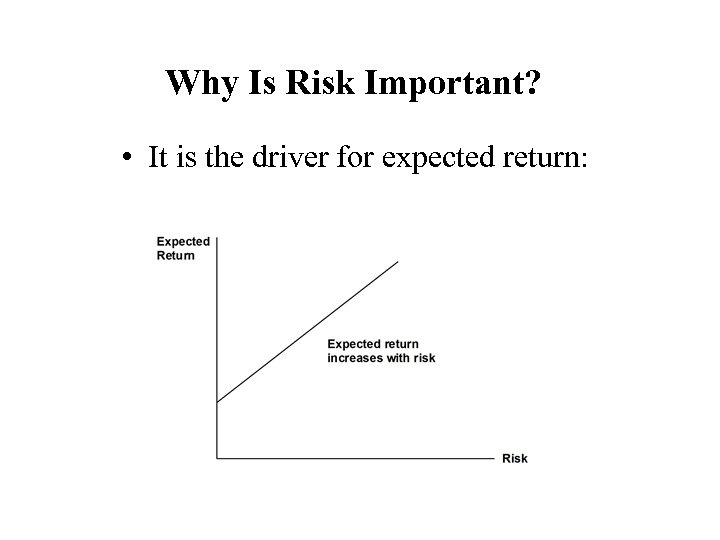Why Is Risk Important? • It is the driver for expected return:

Standard Deviation • Measure of degree of dispersion of distribution - Standard deviation is square root of the variance • Normal distribution - Two times out of three actual value will be within one standard deviation on either side of mean value - 19 out of 20 times will be within two standard deviations - Well diversified portfolios with a large number of stocks have rates of return that approximate a normal distribution

Computing Variance and Standard Deviation Using Historical (ex post) data

Skewness • Distribution of returns have one tail which is longer than the other • Investors prefer returns that are skewed to the right Kurtosis • Measures the “peakedness” of a distribution - leptokurtic refers to a distribution that has a very high center with thick tails - platykurtic is a distribution with short center and negligible tails

Monte Carlo Simulation • Technique using repeated samplings from a probability distribution to determine the distribution of the dollar value of a portfolio - Assumes returns are generated by a random distribution process - Results are dependent upon the mean and standard distribution of the hypothesized distribution - Useful tool to simulate both the accumulation and decumulation of a portfolio

Buying on Margin • Margin rate: percentage of securities purchase that must come from investor’s funds rather than from borrowing • Initial margin rate: used when determining cash needed for new purchase • Maintenance margin rate: used when determining if margin call is needed

Margin Rates • Federal Reserve Board vs. In-house rule • Regulation T – 50% initial margin rate • NYSE's Rule 431 & FINRA's Rule 2520 – 25% maintenance margin rate – 30% on short positions • In-house, only higher, never lower

Buying Power • Dollar value of additional securities that can be purchased on margin with current equity in margin account

Net Equity • Total value of account minus amount of debt outstanding (with respect to a margin account) E = MV – LOAN where MV = market value of portfolio LOAN = current loan balance

Maintenance Margin • Minimum percentage of equity that ongoing margin account is required to maintain at all times MV x (1 – MMR) ≥ LOAN where MMR = maintenance margin rate

Ways to Satisfy Margin Call • Deposit cash in account • Add more collateral (marginable securities) to account. • Sell stock from account and use proceeds to reduce the margin debt In each case, result must raise equity percentage to margin maintenance minimum to satisfy margin call.

Cash Necessary to Meet a Margin Call Cash added = LOAN – [MV x (1 – MMR)] Example: Loan = $50, 000 MV = $60, 000 MMR = 30% Cash added = $50, 000 – [$60, 000 x (1 -. 30)] = $8, 000

Permitted Cash Withdrawals Maximum Cash Withdrawal= MV x (1 – IMR) – LOAN Example: MV = $100, 000, IMR = 60%, LOAN = $15, 000 Max. Cash W/D = $100, 000 x (1 –. 60)–$15, 000 = $25, 000

The Impact of Leverage ROA = (Ending Value – Beginning Value) Beginning Value ROE = {(Ending Value – Beginning Value) – Interest Charges} Initial Investment

Broker Call-Loan Rate • Interest rate charged by banks to brokers for loans that brokers use to support their margin loans to customers • Usually scaled up for margin loan rate