Chapter 19 Option Valuation 2015 Mc Graw-Hill

Chapter 19 Option Valuation © 2015 Mc. Graw-Hill Ryerson Limited

Chapter Summary • Objective: To discuss factors that affect option prices and to present quantitative option pricing models. • • Factors influencing option values Binomial Option Pricing Black-Scholes option valuation Using the Black-Scholes formula © 2015 Mc. Graw-Hill Ryerson Limited 19 -2

Option Values • Intrinsic value - profit that could be made if the option was immediately exercised • • • Call: stock price - exercise price Put: exercise price - stock price Time value - the difference between the option price and the intrinsic value © 2015 Mc. Graw-Hill Ryerson Limited 19 -3

Figure 19. 1 Call Option Value Before Expiration © 2015 Mc. Graw-Hill Ryerson Limited 19 -4

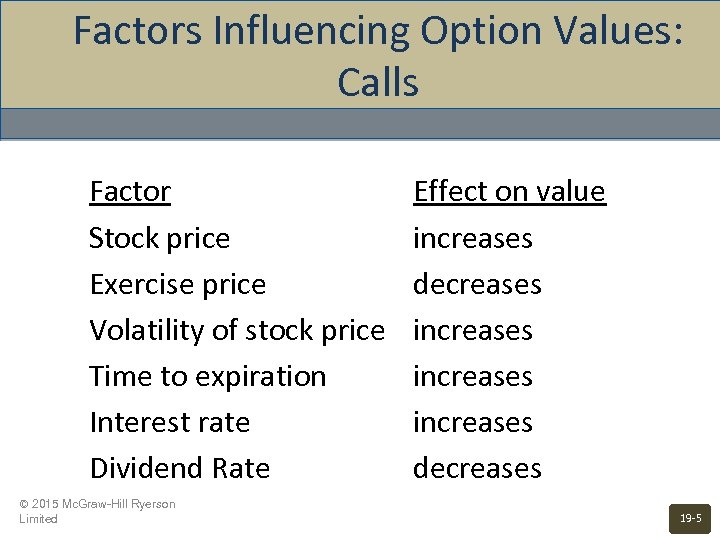Factors Influencing Option Values: Calls Factor Stock price Exercise price Volatility of stock price Time to expiration Interest rate Dividend Rate © 2015 Mc. Graw-Hill Ryerson Limited Effect on value increases decreases increases decreases 19 -5

Restrictions on Option Value: Call • • • Value cannot be negative Value cannot exceed the stock value Value of the call must be greater than the value of levered equity C > S 0 - ( X + D ) / ( 1 + Rf )T C > S 0 - PV ( X ) - PV ( D ) © 2015 Mc. Graw-Hill Ryerson Limited 19 -6

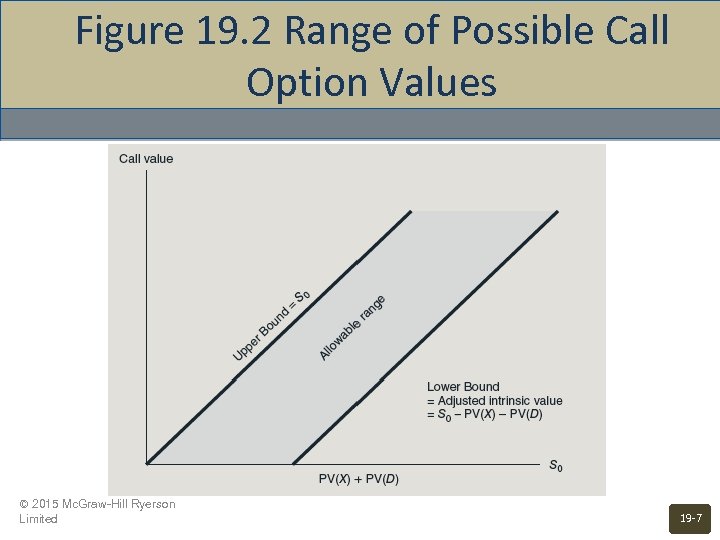Figure 19. 2 Range of Possible Call Option Values © 2015 Mc. Graw-Hill Ryerson Limited 19 -7

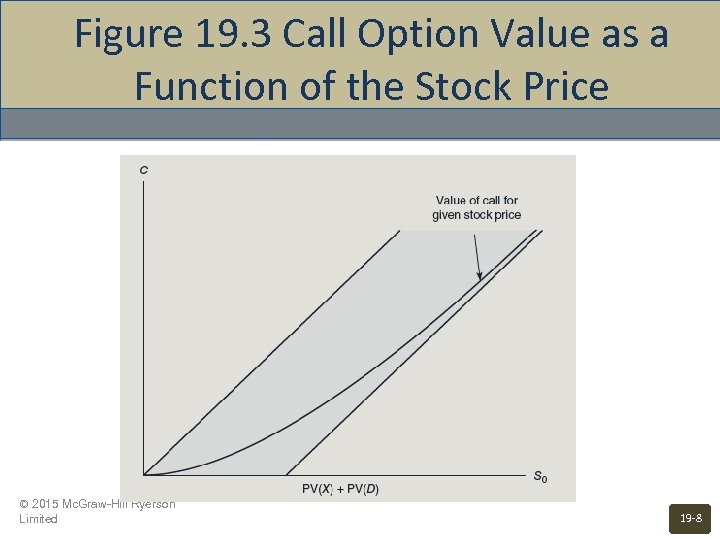Figure 19. 3 Call Option Value as a Function of the Stock Price © 2015 Mc. Graw-Hill Ryerson Limited 19 -8

Early Exercise: Calls • • • The right to exercise an American call early is valueless as long as the stock pays no dividends until the option expires. The value of American and European calls is therefore identical. The call gains value as the stock price rises. Since the price can rise infinitely, the call is “worth more alive than dead. ” © 2015 Mc. Graw-Hill Ryerson Limited 19 -9

Early Exercise: Puts • • American puts are worth more than European puts, all else equal. The possibility of early exercise has value because: • • The value of the stock cannot fall below zero. Once the firm is bankrupt, it is optimal to exercise the American put immediately because of the time value of money. © 2015 Mc. Graw-Hill Ryerson Limited 19 -10

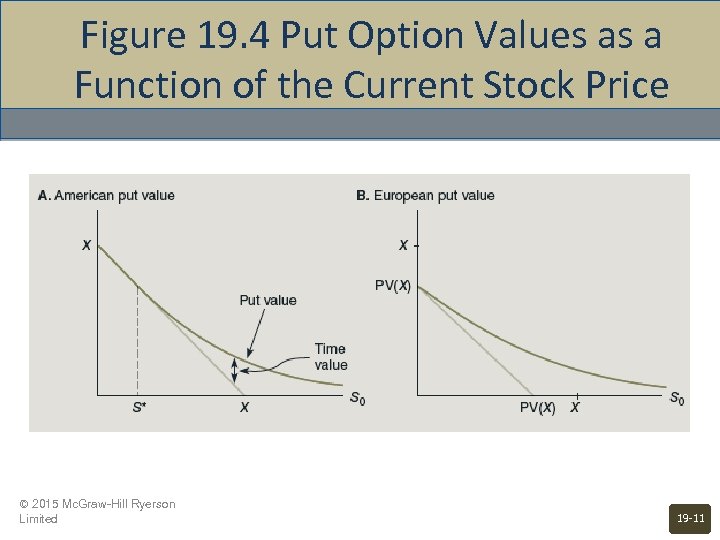Figure 19. 4 Put Option Values as a Function of the Current Stock Price © 2015 Mc. Graw-Hill Ryerson Limited 19 -11

Summary Reminder • Objective: To discuss factors that affect option prices and to present quantitative option pricing models. ü Factors influencing option values • • • Binomial Option Pricing Black-Scholes option valuation Using the Black-Scholes formula © 2015 Mc. Graw-Hill Ryerson Limited 19 -12

Binomial Option Pricing: Text Example u=1. 20 D=. 90 10 120 100 C 90 Stock Price © 2015 Mc. Graw-Hill Ryerson Limited 0 Call Option Payoff X = 110 19 -13

Binomial Option Pricing: Text Example Alternative Portfolio Buy 1 share of stock at $100 Borrow $81. 82 (10% Rate) Net outlay $18. 18 Payoff Value of Stock 90 120 Repay loan - 90 -90 Net Payoff 0 30 © 2015 Mc. Graw-Hill Ryerson Limited Payoff Structure is exactly 3 times the Call 19 -14

Binomial Option Pricing: Text Example 30 18. 18 30 C 0 0 3 C = $18. 18 C = $6. 06 © 2015 Mc. Graw-Hill Ryerson Limited 19 -15

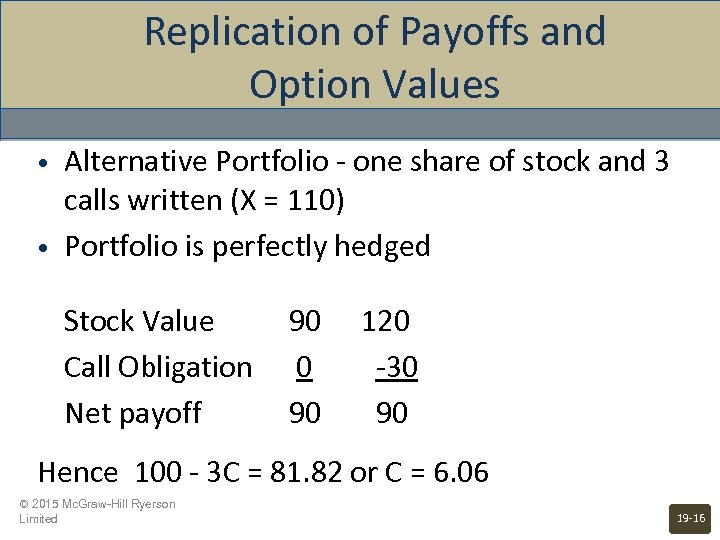Replication of Payoffs and Option Values • • Alternative Portfolio - one share of stock and 3 calls written (X = 110) Portfolio is perfectly hedged Stock Value Call Obligation Net payoff 90 120 0 -30 90 Hence 100 - 3 C = 81. 82 or C = 6. 06 © 2015 Mc. Graw-Hill Ryerson Limited 19 -16

Hedge Ratio • • In the example, the hedge ratio = 1 share to 3 calls or 1/3. Generally, the hedge ratio is: © 2015 Mc. Graw-Hill Ryerson Limited 19 -17

Generalizing the Two-State Approach • • Assume that we can break the year into two sixmonth segments In each six-month segment the stock could increase by 10% or decrease by 5% Assume the stock is initially selling at 100 Possible outcomes • • • Increase by 10% twice Decrease by 5% twice Increase once and decrease once (2 paths) © 2015 Mc. Graw-Hill Ryerson Limited 19 -18

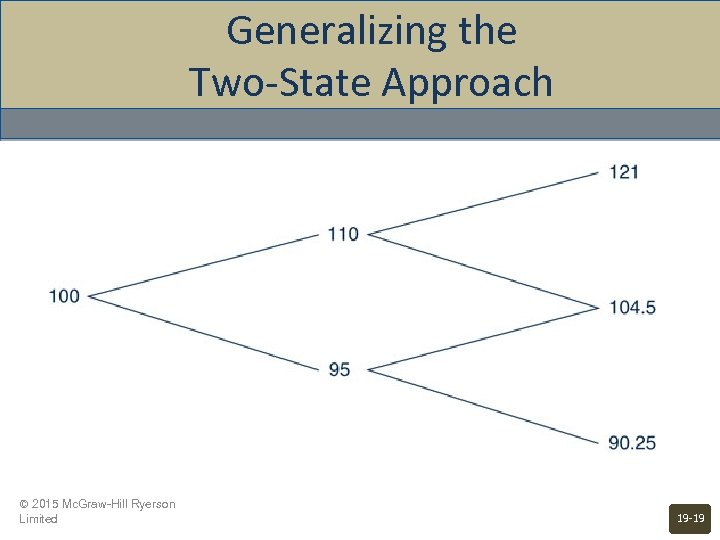Generalizing the Two-State Approach © 2015 Mc. Graw-Hill Ryerson Limited 19 -19

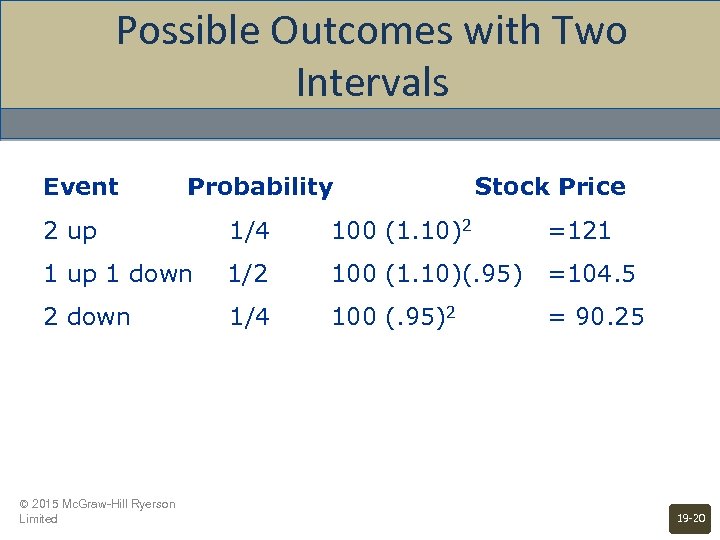Possible Outcomes with Two Intervals Event Probability Stock Price 2 up 1/4 100 (1. 10)2 =121 1 up 1 down 1/2 100 (1. 10)(. 95) =104. 5 2 down 1/4 100 (. 95)2 = 90. 25 © 2015 Mc. Graw-Hill Ryerson Limited 19 -20

Making the Valuation Model Practical • © 2015 Mc. Graw-Hill Ryerson Limited 19 -21

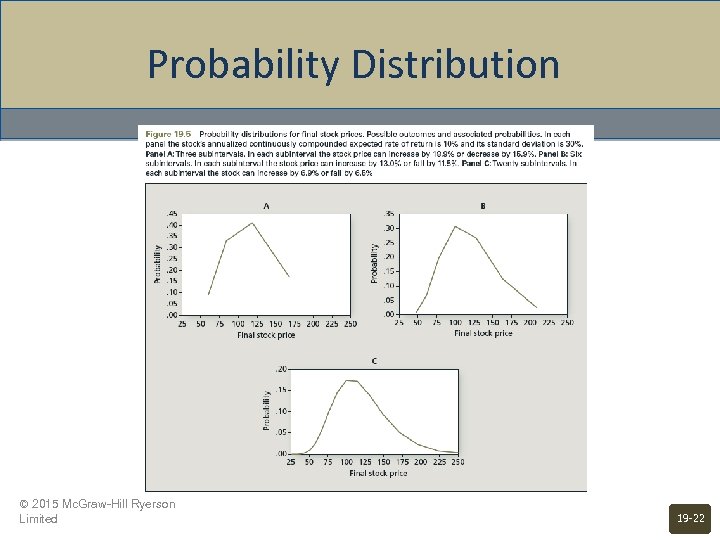Probability Distribution © 2015 Mc. Graw-Hill Ryerson Limited 19 -22

Summary Reminder • Objective: To discuss factors that affect option prices and to present quantitative option pricing models. ü Factors influencing option values ü Binomial Option Pricing • • Black-Scholes option valuation Using the Black-Scholes formula © 2015 Mc. Graw-Hill Ryerson Limited 19 -23

Black-Scholes Option Valuation Co = So. N(d 1) - Xe-r. TN(d 2) d 1 = [ln(So/X) + (r + 2/2)T] / ( T 1/2) d 2 = d 1 + ( T 1/2) where, Co = Current call option value So = Current stock price N(d) = probability that a random draw from a normal distribution will be less than d © 2015 Mc. Graw-Hill Ryerson Limited 19 -24

Black-Scholes Option Valuation (cont’d) X = Exercise price e = 2. 71828, the base of the natural log r = Risk-free interest rate (annualizes continuously compounded with the same maturity as the option) T = time to maturity of the option in years ln = Natural log function Standard deviation of annualized continuously compounded rate of return on the stock © 2015 Mc. Graw-Hill Ryerson Limited 19 -25

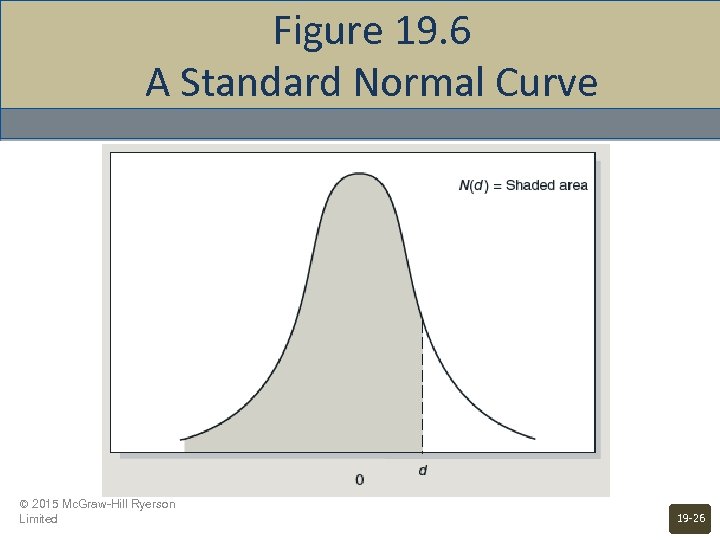Figure 19. 6 A Standard Normal Curve © 2015 Mc. Graw-Hill Ryerson Limited 19 -26

Call Option Example So = 100 r = . 10 = . 50 © 2015 Mc. Graw-Hill Ryerson Limited X = 95 T = . 25 (quarter) 19 -27

Probabilities from Normal Distribution Using a table or the NORMDIST function in Excel, we find that N (. 43) =. 6664 and N (. 18) =. 5714. Therefore: Co = So. N(d 1) - Xe-r. TN(d 2) Co = 100 X. 6664 - 95 e-. 10 X. 25 X. 5714 Co = $13. 70 © 2015 Mc. Graw-Hill Ryerson Limited 19 -28

Call Option Value Implied Volatility • Implied volatility is volatility for the stock implied by the option price. • Using Black-Scholes and the actual price of the option, solve for volatility. • Is the implied volatility consistent with the stock? © 2015 Mc. Graw-Hill Ryerson Limited 19 -29

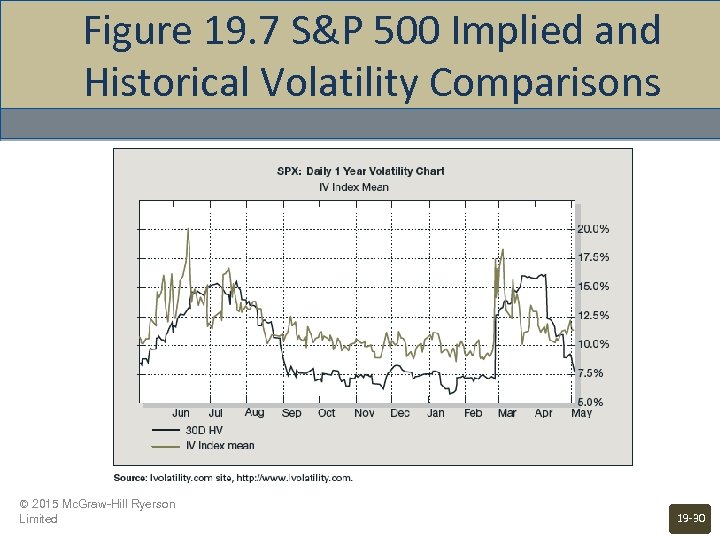Figure 19. 7 S&P 500 Implied and Historical Volatility Comparisons © 2015 Mc. Graw-Hill Ryerson Limited 19 -30

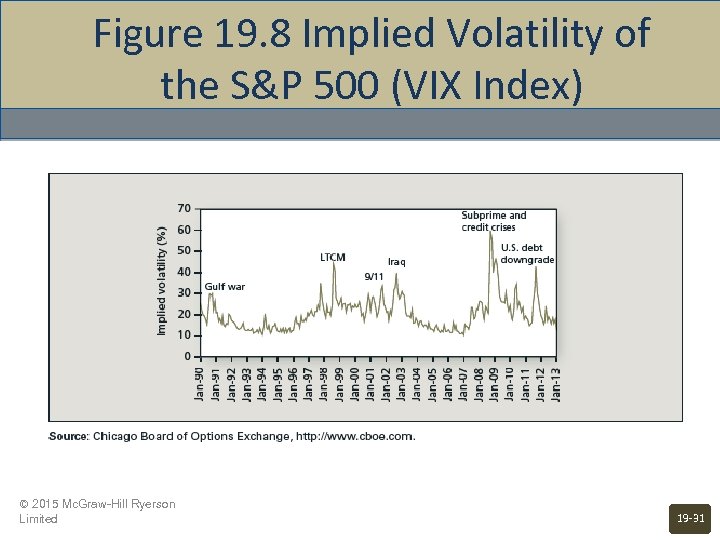Figure 19. 8 Implied Volatility of the S&P 500 (VIX Index) © 2015 Mc. Graw-Hill Ryerson Limited 19 -31

Black-Scholes Model with Dividends • • • The Black Scholes call option formula applies to stocks that do not pay dividends. What if dividends ARE paid? One approach is to replace the stock price with a dividend adjusted stock price Replace S 0 with S 0 - PV (Dividends) © 2015 Mc. Graw-Hill Ryerson Limited 19 -32

Example 19. 5 Black-Scholes Put Valuation P = Xe-r. T [1 -N(d 2)] - S 0 [1 -N(d 1)] Using Example 19. 4 data S = 100 r =. 10 X = 95 =. 5 T =. 25 P= 95 e-10 x. 25(1 -. 5714)-100(1 -. 6664)=6. 35 © 2015 Mc. Graw-Hill Ryerson Limited 19 -33

Put Option Valuation: Using Put-Call Parity P = C + PV (X) - So = C + Xe-r. T - So Using the example data C = 13. 70 X = 95 S = 100 r =. 10 T = . 25 P = 13. 70 + 95 e -. 10 x. 25 - 100 P = 6. 35 © 2015 Mc. Graw-Hill Ryerson Limited 19 -34

Summary Reminder • Objective: To discuss factors that affect option prices and to present quantitative option pricing models. ü Factors influencing option values ü Binomial Option Pricing ü Black-Scholes option valuation • © 2015 Mc. Graw-Hill Ryerson Limited Using the Black-Scholes formula 19 -35

Using the Black-Scholes Formula Hedging: Hedge ratio or delta • The number of stocks required to hedge against the price risk of holding one option Call = N (d 1) Put = N (d 1) - 1 Option Elasticity • Percentage change in the option’s value given a 1% change in the value of the underlying stock © 2015 Mc. Graw-Hill Ryerson Limited 19 -36

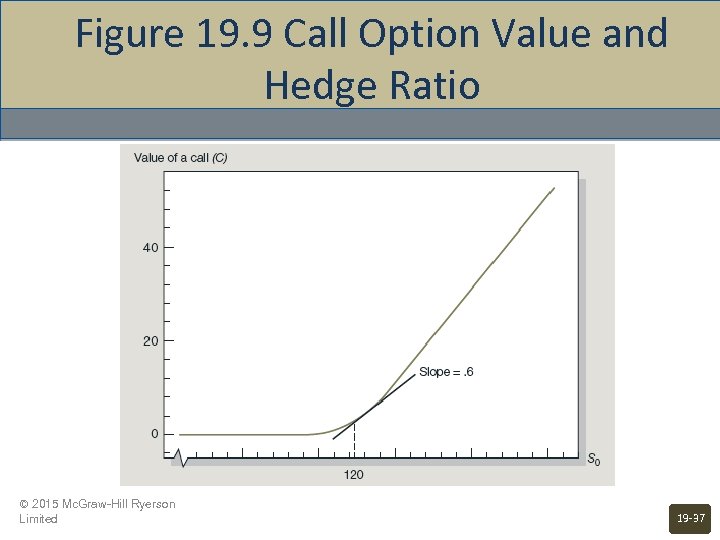Figure 19. 9 Call Option Value and Hedge Ratio © 2015 Mc. Graw-Hill Ryerson Limited 19 -37

Portfolio Insurance - Protecting Against Declines in Stock Value • • Buying Puts - results in downside protection with unlimited upside potential Limitations • • • Tracking errors if indexes are used for the puts Maturity of puts may be too short Hedge ratios or deltas change as stock values change © 2015 Mc. Graw-Hill Ryerson Limited 19 -38

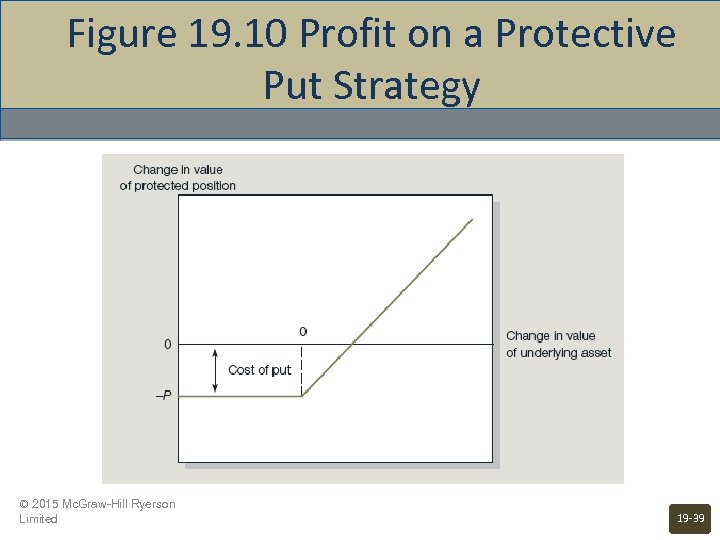Figure 19. 10 Profit on a Protective Put Strategy © 2015 Mc. Graw-Hill Ryerson Limited 19 -39

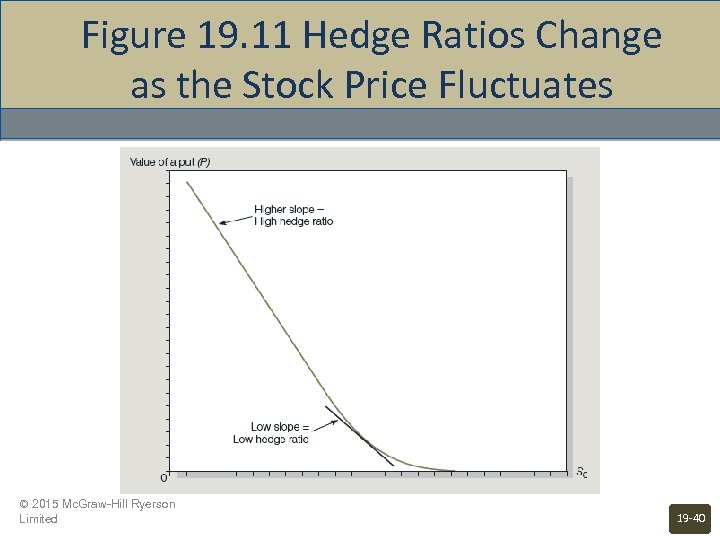Figure 19. 11 Hedge Ratios Change as the Stock Price Fluctuates © 2015 Mc. Graw-Hill Ryerson Limited 19 -40

Option Pricing, 08 - 09 Crisis • Merton’s insight into the financial crisis • • • When banks lend, they implicitly write a put option to the borrow. Borrower’s ability to satisfy the loan by transferring ownership is the right to “sell” itself to the creditor. CDS provide an even clearer example • • Figure 19. 13 When firm is strong, slope is zero, but if firm slips the implicit put rises and slope is now steeper. © 2015 Mc. Graw-Hill Ryerson Limited 19 -41

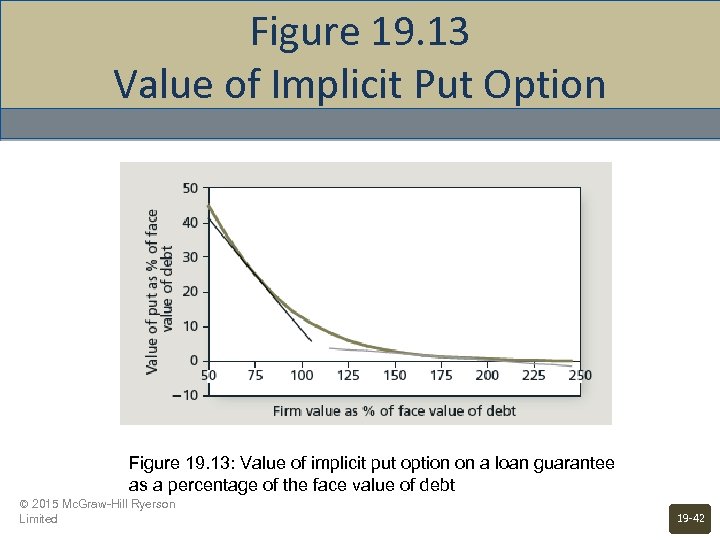Figure 19. 13 Value of Implicit Put Option Figure 19. 13: Value of implicit put option on a loan guarantee as a percentage of the face value of debt © 2015 Mc. Graw-Hill Ryerson Limited 19 -42

Hedging Bets on Mispriced Options • • Option value is positively related to volatility If an investor believes that the volatility that is implied in an option’s price is too low, a profitable trade is possible Profit must be hedged against a decline in the value of the stock Performance depends on option price relative to the implied volatility © 2015 Mc. Graw-Hill Ryerson Limited 19 -43

Hedging and Delta • • The appropriate hedge will depend on the delta. Recall the delta is the change in the value of the option relative to the change in the value of the stock. © 2015 Mc. Graw-Hill Ryerson Limited 19 -44

Mispriced Option: Example 19. 8 Implied volatility = 33% Investor believes volatility should = 35% Option maturity Put price P = 60 days = $4. 495 Exercise price and stock price = $90 Risk-free rate r Delta © 2015 Mc. Graw-Hill Ryerson Limited = 4% = -. 453 19 -45

Hedged Put Portfolio Cost to establish the hedged position 1000 put options at $4. 495 / option $ 4, 495 453 shares at $90 / share Total outlay © 2015 Mc. Graw-Hill Ryerson Limited 40, 770 45, 265 19 -46

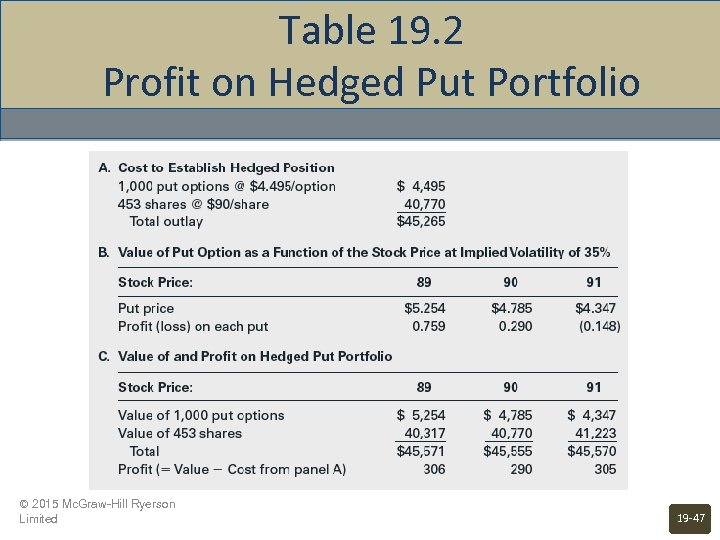Table 19. 2 Profit on Hedged Put Portfolio © 2015 Mc. Graw-Hill Ryerson Limited 19 -47

Example 19. 8 Conclusions • • As the stock price changes, so do the deltas used to calculate the hedge ratio. Gamma = sensitivity of the delta to the stock price. • • • Gamma is similar to bond convexity. The hedge ratio will change with market conditions. Rebalancing is necessary. © 2015 Mc. Graw-Hill Ryerson Limited 19 -48

Delta Neutral • When you establish a position in stocks and options that is hedged with respect to fluctuations in the price of the underlying asset, your portfolio is said to be delta neutral. • The portfolio does not change value when the stock price fluctuates. © 2015 Mc. Graw-Hill Ryerson Limited 19 -49

Table 19. 3 Profits on Delta. Neutral Options Portfolio © 2015 Mc. Graw-Hill Ryerson Limited 19 -50

Stochastic Dominance Option Pricing • • • Suppose the stock price can take three or more values at the end of the period Then the market becomes incomplete It is not possible to replicate the option with the stock and borrowed funds There is no single option price in this model There are, however, option bounds that can be derived, that depend on the distribution of possible stock values © 2015 Mc. Graw-Hill Ryerson Limited 19 -51

Empirical Evidence on Option Pricing • • B-S model shows some persistent empirical failures of the model to represent actual prices of traded options. Biggest concern is volatility • • • The implied volatility of all options on a given stock with the same expiration date should be equal. Empirical test show that implied volatility actually falls as exercise price increases. This may be due to fears of a market crash. © 2015 Mc. Graw-Hill Ryerson Limited 19 -52