744d1b2c7626578f08a4b5f716b70996.ppt
- Количество слайдов: 72
 CHAPTER 18 & 19 ELECTRIC FIELD, ELECTRICAL ENERGY and CAPACITANCE
CHAPTER 18 & 19 ELECTRIC FIELD, ELECTRICAL ENERGY and CAPACITANCE
 Michael Faraday developed the concept of electric field. A charge creates an electric field about it in all directions. When another charged object enters this electric field, it experiences an electric force.
Michael Faraday developed the concept of electric field. A charge creates an electric field about it in all directions. When another charged object enters this electric field, it experiences an electric force.
 Suppose I have a +Q charge. I want to know the strength of the electric field (E) at a point which is a distance r from it.
Suppose I have a +Q charge. I want to know the strength of the electric field (E) at a point which is a distance r from it.
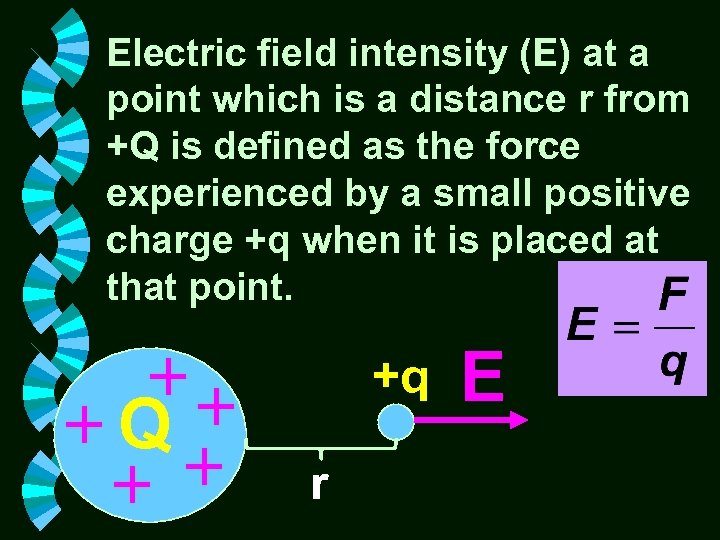 Electric field intensity (E) at a point which is a distance r from +Q is defined as the force experienced by a small positive charge +q when it is placed at that point. Q +q r E
Electric field intensity (E) at a point which is a distance r from +Q is defined as the force experienced by a small positive charge +q when it is placed at that point. Q +q r E
 The direction of the electric field intensity at a point is the same as the direction in which a positive charge +q would move when placed at that point.
The direction of the electric field intensity at a point is the same as the direction in which a positive charge +q would move when placed at that point.
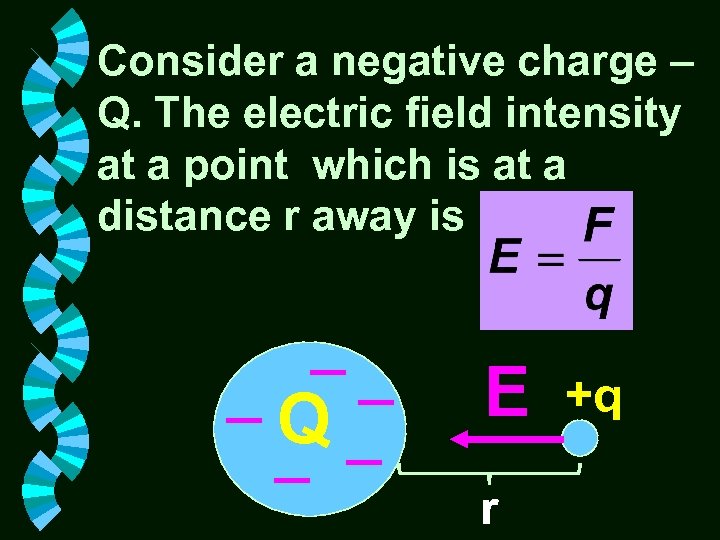 Consider a negative charge – Q. The electric field intensity at a point which is at a distance r away is Q E r +q
Consider a negative charge – Q. The electric field intensity at a point which is at a distance r away is Q E r +q
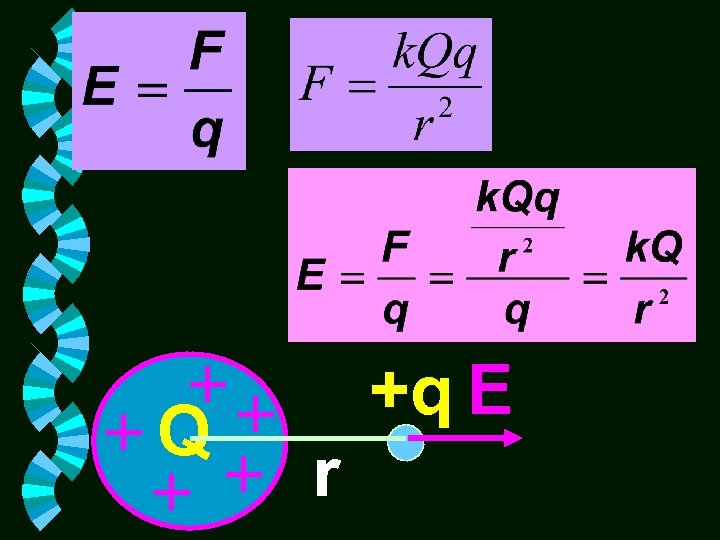 Q +q E r
Q +q E r
 Electric field Lines are imaginary lines drawn in such a manner that their direction at any point is the same as the direction of the electric field at that point. The strength of the electric field is indicated by the spacing between the lines. The closer the electric field lines the stronger is the electric field.
Electric field Lines are imaginary lines drawn in such a manner that their direction at any point is the same as the direction of the electric field at that point. The strength of the electric field is indicated by the spacing between the lines. The closer the electric field lines the stronger is the electric field.
 Consider a positive charge. The electric field lines around it will point away from the charge.
Consider a positive charge. The electric field lines around it will point away from the charge.
 Consider a negative charge. The electric field lines around it will point towards the charge.
Consider a negative charge. The electric field lines around it will point towards the charge.
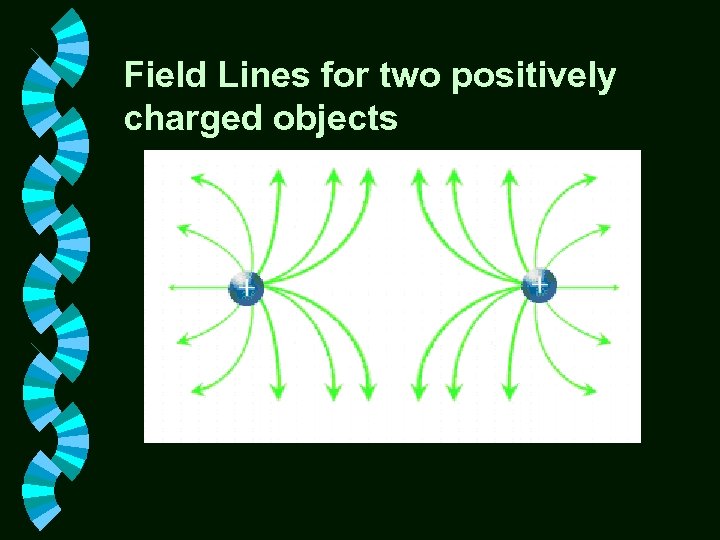 Field Lines for two positively charged objects
Field Lines for two positively charged objects
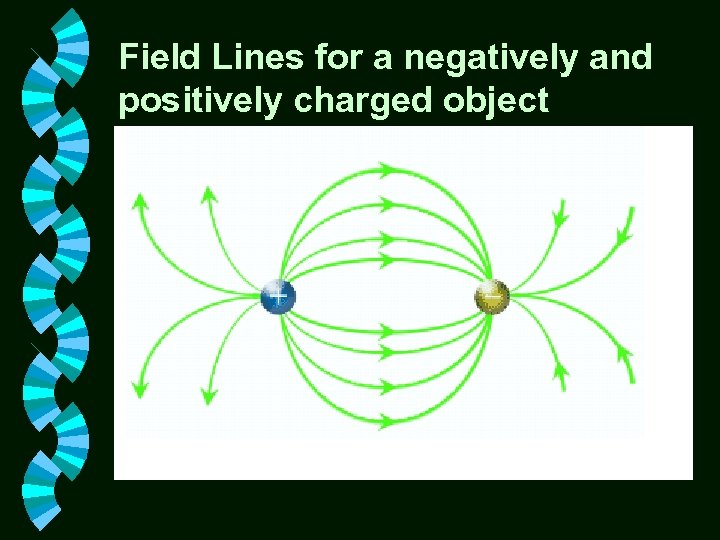 Field Lines for a negatively and positively charged object
Field Lines for a negatively and positively charged object
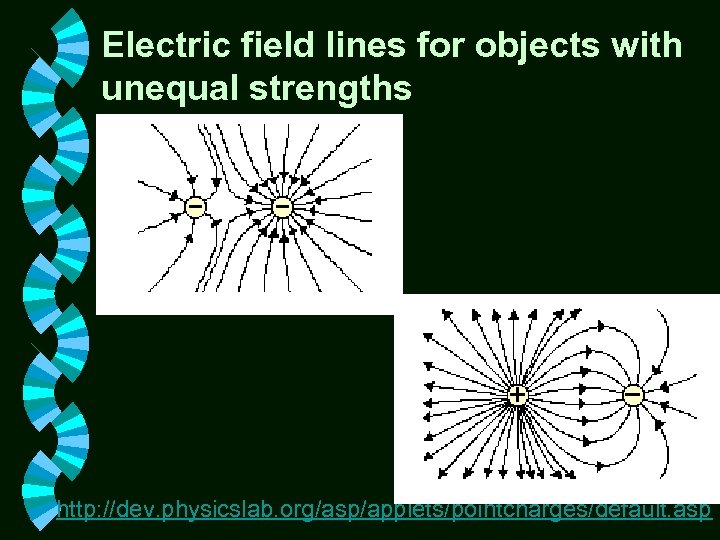 Electric field lines for objects with unequal strengths http: //dev. physicslab. org/asp/applets/pointcharges/default. asp
Electric field lines for objects with unequal strengths http: //dev. physicslab. org/asp/applets/pointcharges/default. asp
 Example What is the electric field intensity at a distance 2 m from a charge -12 x 10 -6 C?
Example What is the electric field intensity at a distance 2 m from a charge -12 x 10 -6 C?
 Problem #1 A negative charge of 2 x 10 -8 C experiences a force of 0. 060 N to the right in an electric field. What is the magnitude of the electric field?
Problem #1 A negative charge of 2 x 10 -8 C experiences a force of 0. 060 N to the right in an electric field. What is the magnitude of the electric field?
 Problem #2 A positive test charge of 5 x 10 -4 C is in an electric field that exerts a force of 2. 5 x 10 -4 N on it. What is the magnitude of the electric field at the location of the test charge?
Problem #2 A positive test charge of 5 x 10 -4 C is in an electric field that exerts a force of 2. 5 x 10 -4 N on it. What is the magnitude of the electric field at the location of the test charge?
 Problem #3 What charge exists on a test charge that experiences a force of 1. 4 x 10 -8 N at a point where the electric field intensity is 2. 0 x 104 N/C?
Problem #3 What charge exists on a test charge that experiences a force of 1. 4 x 10 -8 N at a point where the electric field intensity is 2. 0 x 104 N/C?
 Problem #4 Find the electric field intensity at a point P, located 6 mm to the left of a point charge of 8 C. What are the magnitude and direction of the force on a – 2 n. C charge placed at a point P. 6 mm p Q 8 x 10 -6 C
Problem #4 Find the electric field intensity at a point P, located 6 mm to the left of a point charge of 8 C. What are the magnitude and direction of the force on a – 2 n. C charge placed at a point P. 6 mm p Q 8 x 10 -6 C
 6 mm p Q 8 x 10 -6 C
6 mm p Q 8 x 10 -6 C
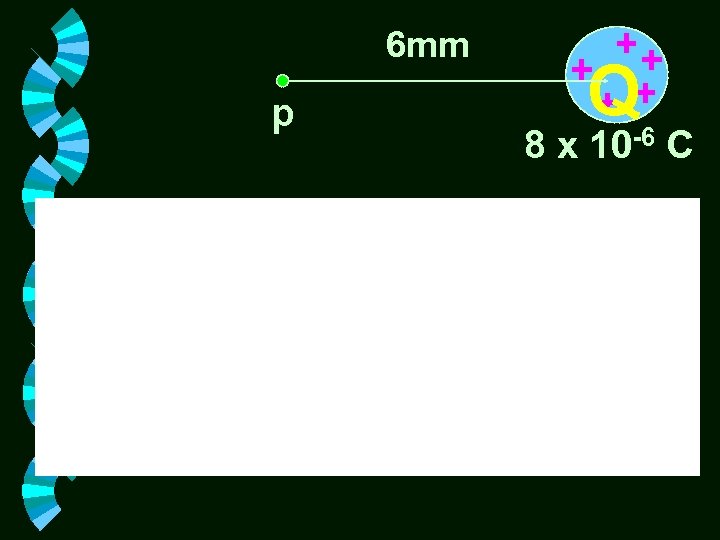 6 mm p Q 8 x 10 -6 C
6 mm p Q 8 x 10 -6 C
 Problem #5 Determine the electric field intensity at the midpoint between a – 60 C charge and a + 40 C charge. The charges are 70 mm apart in air. A EA p -60 x 10 -6 C EB B 40 x 10 -6 C
Problem #5 Determine the electric field intensity at the midpoint between a – 60 C charge and a + 40 C charge. The charges are 70 mm apart in air. A EA p -60 x 10 -6 C EB B 40 x 10 -6 C
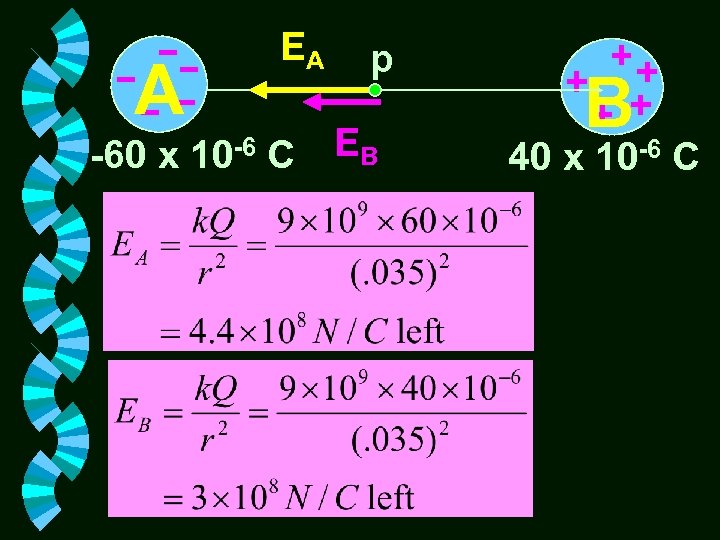 A EA p -60 x 10 -6 C EB B 40 x 10 -6 C
A EA p -60 x 10 -6 C EB B 40 x 10 -6 C
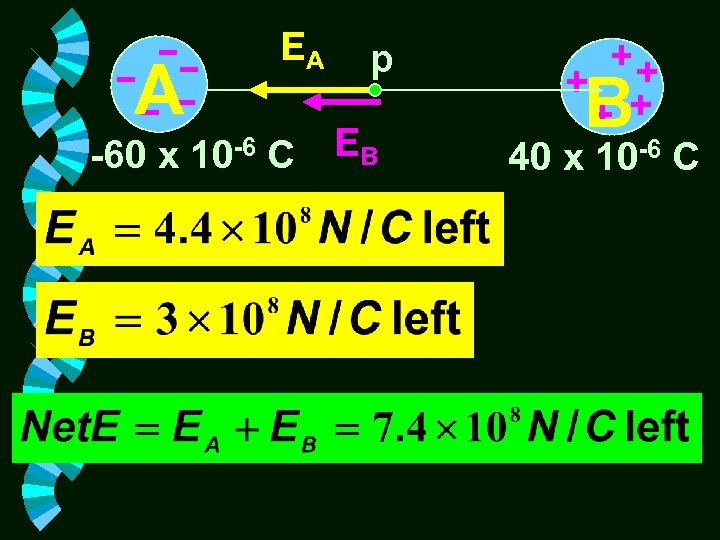 A EA p -60 x 10 -6 C EB B 40 x 10 -6 C
A EA p -60 x 10 -6 C EB B 40 x 10 -6 C
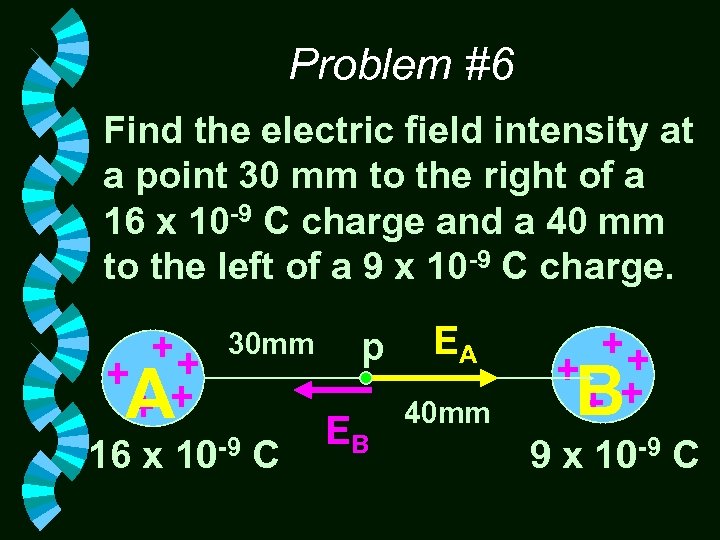 Problem #6 Find the electric field intensity at a point 30 mm to the right of a 16 x 10 -9 C charge and a 40 mm to the left of a 9 x 10 -9 C charge. A 30 mm 16 x 10 -9 C p EB EA 40 mm B 9 x 10 -9 C
Problem #6 Find the electric field intensity at a point 30 mm to the right of a 16 x 10 -9 C charge and a 40 mm to the left of a 9 x 10 -9 C charge. A 30 mm 16 x 10 -9 C p EB EA 40 mm B 9 x 10 -9 C
 A 30 mm 16 x 10 -9 C p EB EA 40 mm B 9 x 10 -9 C
A 30 mm 16 x 10 -9 C p EB EA 40 mm B 9 x 10 -9 C
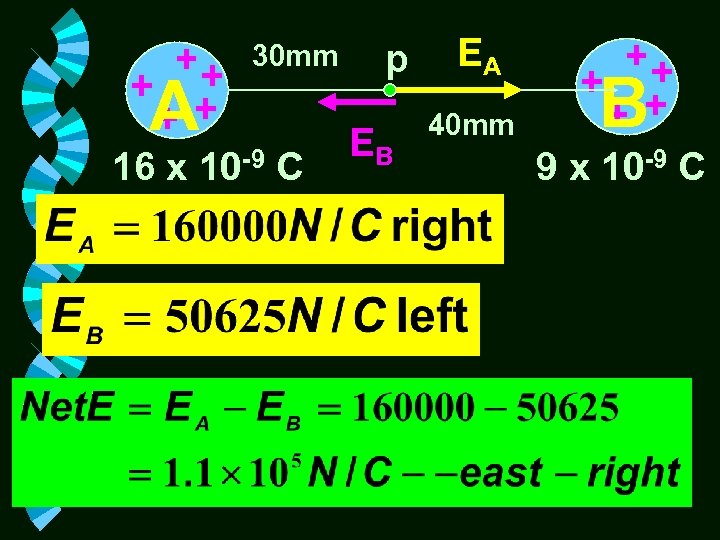 A 30 mm 16 x 10 -9 C p EB EA 40 mm B 9 x 10 -9 C
A 30 mm 16 x 10 -9 C p EB EA 40 mm B 9 x 10 -9 C
 Problem #7 Two charges of +16 x 10 -6 C and +8 x 10 -6 C are 200 mm apart in air. At what point between the two charges is the field intensity equal to zero?
Problem #7 Two charges of +16 x 10 -6 C and +8 x 10 -6 C are 200 mm apart in air. At what point between the two charges is the field intensity equal to zero?
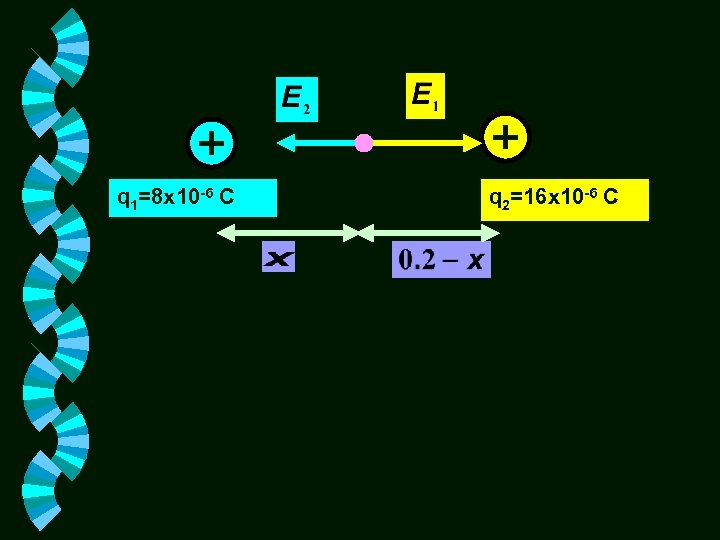 q 1=8 x 10 -6 C q 2=16 x 10 -6 C
q 1=8 x 10 -6 C q 2=16 x 10 -6 C

 CONDUCTORS IN ELECTROSTATIC EQUILIBRIUM A good conductor contains charges that are not bound to any atom and are free to move about within the material. When no net motion of charges occurs within a conductor, the conductor is said to be in electrostatic equillibrium.
CONDUCTORS IN ELECTROSTATIC EQUILIBRIUM A good conductor contains charges that are not bound to any atom and are free to move about within the material. When no net motion of charges occurs within a conductor, the conductor is said to be in electrostatic equillibrium.
 AN ISOLATED CONDUCTOR HAS THE FOLLOWING PROPERTIES 1. The electric field is zero everywhere inside the conductor. 2. Any excess charge on an isolated conductor resides entirely on its surface.
AN ISOLATED CONDUCTOR HAS THE FOLLOWING PROPERTIES 1. The electric field is zero everywhere inside the conductor. 2. Any excess charge on an isolated conductor resides entirely on its surface.
 AN ISOLATED CONDUCTOR HAS THE FOLLOWING PROPERTIES 3. The electric field just outside a charged conductor is perpendicular to the conductor’s surface. 4. On an irregularly shaped conductor, the charge tends to accumulate at sharp points.
AN ISOLATED CONDUCTOR HAS THE FOLLOWING PROPERTIES 3. The electric field just outside a charged conductor is perpendicular to the conductor’s surface. 4. On an irregularly shaped conductor, the charge tends to accumulate at sharp points.
 CHAPTER 19 HOORAY!!!
CHAPTER 19 HOORAY!!!
 ENERGY & ELECTRIC POTENTIAL Point A Point B Consider a fixed positive charge placed at a point A and a fixed negative charge at point B. There is a force of attraction between the two charges.
ENERGY & ELECTRIC POTENTIAL Point A Point B Consider a fixed positive charge placed at a point A and a fixed negative charge at point B. There is a force of attraction between the two charges.
 ENERGY & ELECTRIC POTENTIAL Point A Point B Point C Therefore to bring the charge at B to a point C a distance (r) from B, will require work to be done against the force of attraction. Thus the charge at B will undergo a change in potential energy.
ENERGY & ELECTRIC POTENTIAL Point A Point B Point C Therefore to bring the charge at B to a point C a distance (r) from B, will require work to be done against the force of attraction. Thus the charge at B will undergo a change in potential energy.
 ELECTRICAL POTENTIAL DIFFERENCE IS MEASURED IN VOLTS IT IS THE CHANGE IN POTENTIAL ENERGY PER UNIT CHARGE.
ELECTRICAL POTENTIAL DIFFERENCE IS MEASURED IN VOLTS IT IS THE CHANGE IN POTENTIAL ENERGY PER UNIT CHARGE.
 This formula is used when dealing with charges
This formula is used when dealing with charges
 This formula is used when working with parallel plates
This formula is used when working with parallel plates
 This formula is used when work on a charge is given
This formula is used when work on a charge is given
 Example The electric field intensity between the two charged parallel plates is 8000 N/C. The plates are 0. 05 m apart. What is the potential difference between the two plates?
Example The electric field intensity between the two charged parallel plates is 8000 N/C. The plates are 0. 05 m apart. What is the potential difference between the two plates?
 Problem #1 A voltmeter reads 500 V when placed across two charged, parallel metal plates. The plates are 0. 02 m apart. What is the electric field between them?
Problem #1 A voltmeter reads 500 V when placed across two charged, parallel metal plates. The plates are 0. 02 m apart. What is the electric field between them?

 Problem #2 What work is done on a 5 C charge that is raised by a potential of 1. 5 V
Problem #2 What work is done on a 5 C charge that is raised by a potential of 1. 5 V
 Problem #3 If 120 J of work is done to move one Coulomb of charge from a positive plate to a negative plate, what voltage difference exists between the plates?
Problem #3 If 120 J of work is done to move one Coulomb of charge from a positive plate to a negative plate, what voltage difference exists between the plates?
 Problem #4 How much work is done to transfer 0. 15 C of charge through a potential difference of 9 V?
Problem #4 How much work is done to transfer 0. 15 C of charge through a potential difference of 9 V?
 Problem #5 An electron is moved through a potential difference of 500 V. How much work is done on the electron?
Problem #5 An electron is moved through a potential difference of 500 V. How much work is done on the electron?
 Problem #6 A force of 0. 053 N is required to move a charge of 37 x 10 -6 C a distance of 25 cm in an electric field. What is the size of the potential difference between the two points?
Problem #6 A force of 0. 053 N is required to move a charge of 37 x 10 -6 C a distance of 25 cm in an electric field. What is the size of the potential difference between the two points?
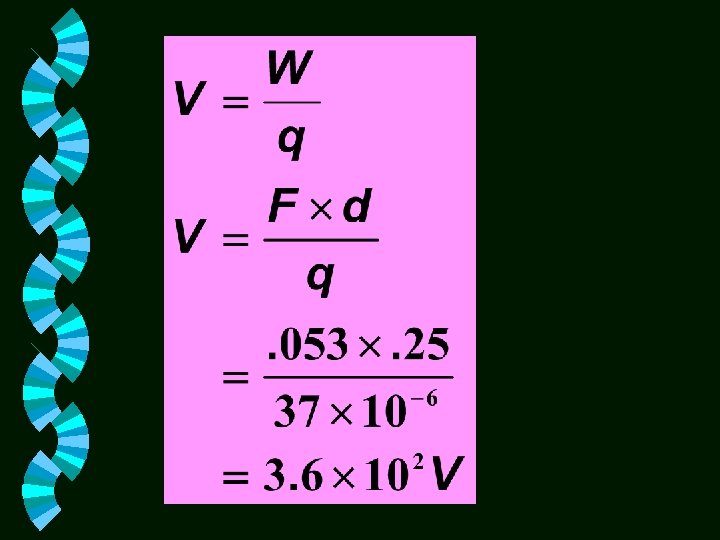
 Parallel Plates When two parallel plates are connected across a battery, the plates will become charged an electric field will be established between them.
Parallel Plates When two parallel plates are connected across a battery, the plates will become charged an electric field will be established between them.
 The direction of an electric field is defined as the direction that a positive test charge would move. So in this case, the electric field would point from the positive plate to the negative plate. The field lines are parallel to each other and hence this type of electric field is uniform and is calculated with the equation E = V / d.
The direction of an electric field is defined as the direction that a positive test charge would move. So in this case, the electric field would point from the positive plate to the negative plate. The field lines are parallel to each other and hence this type of electric field is uniform and is calculated with the equation E = V / d.
 V = Volts E = N/Cd = m Therefore 1 N/C = 1 V/m
V = Volts E = N/Cd = m Therefore 1 N/C = 1 V/m
 Since the field lines are parallel and the electric field is uniform between two parallel plates, a test charge would experience the same force of attraction or repulsion no matter where it was located. That force is calculated with the equation F = q E.
Since the field lines are parallel and the electric field is uniform between two parallel plates, a test charge would experience the same force of attraction or repulsion no matter where it was located. That force is calculated with the equation F = q E.
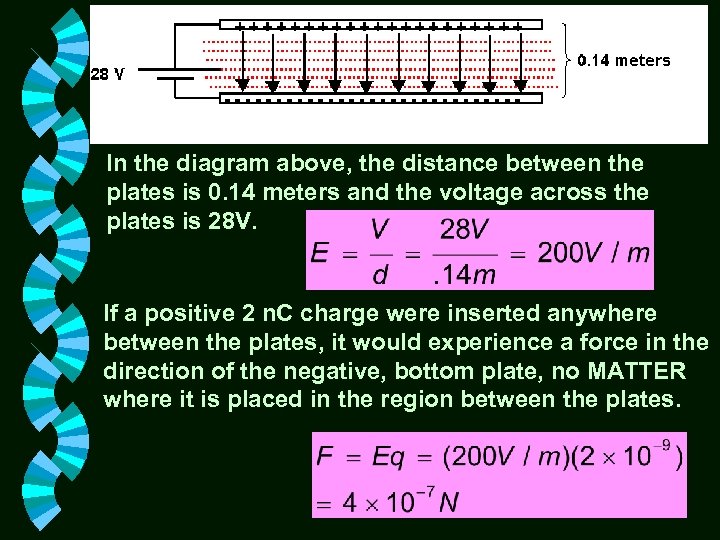 In the diagram above, the distance between the plates is 0. 14 meters and the voltage across the plates is 28 V. If a positive 2 n. C charge were inserted anywhere between the plates, it would experience a force in the direction of the negative, bottom plate, no MATTER where it is placed in the region between the plates.
In the diagram above, the distance between the plates is 0. 14 meters and the voltage across the plates is 28 V. If a positive 2 n. C charge were inserted anywhere between the plates, it would experience a force in the direction of the negative, bottom plate, no MATTER where it is placed in the region between the plates.

 Millikan Oil Drop Experiment Millikan found the charge of an electron. • Fine oil drops were sprayed from an atomizer in the air. Gravity acting on the drops caused them to fall. A potential difference was placed across the plates. The resulting electric field between the plates exerted a force on the charged drops. The resulting electric field between the plates was adjusted to suspend a charged drop between the plates. •
Millikan Oil Drop Experiment Millikan found the charge of an electron. • Fine oil drops were sprayed from an atomizer in the air. Gravity acting on the drops caused them to fall. A potential difference was placed across the plates. The resulting electric field between the plates exerted a force on the charged drops. The resulting electric field between the plates was adjusted to suspend a charged drop between the plates. •
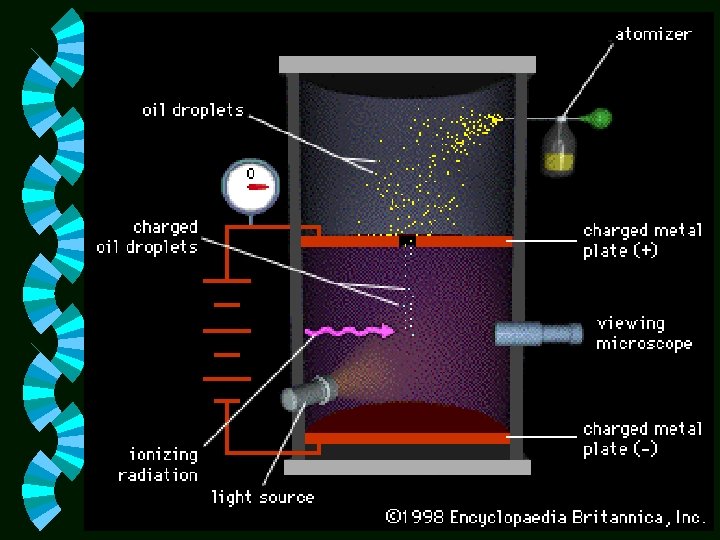
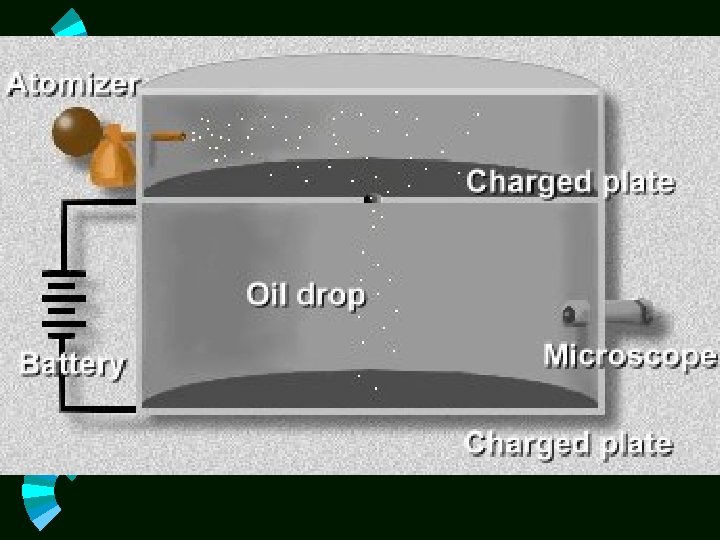
 Each electron always carries the same charge. w Charges are quantized w Changes in charges are caused by one or more electrons being added or removed. w
Each electron always carries the same charge. w Charges are quantized w Changes in charges are caused by one or more electrons being added or removed. w
 Example An oil drop weighs 1. 9 x 10 -15 N. It is suspended in an electric field of 6 x 103 N/C. What is the charge of the drop? How many excess electrons does it carry?
Example An oil drop weighs 1. 9 x 10 -15 N. It is suspended in an electric field of 6 x 103 N/C. What is the charge of the drop? How many excess electrons does it carry?
 Problem #7 A positively charged oil drop weighs 6. 4 x 10 -13 N. An electric field of 4 x 106 N/C suspends the drop. A) What is the charge on the drop? B) How many electrons are in the drop?
Problem #7 A positively charged oil drop weighs 6. 4 x 10 -13 N. An electric field of 4 x 106 N/C suspends the drop. A) What is the charge on the drop? B) How many electrons are in the drop?
 Problem #8 A charged particle of mass 2 x 10 -9 kg and a charge of 2 x 10 -6 C is placed next to one of the two parallel plates 10 cm apart with a 2000 N/C electric field intensity. A) What is the acceleration that the particle gets because of the force due to the electric field between the plates? B) What is the speed of the particle at the other plate?
Problem #8 A charged particle of mass 2 x 10 -9 kg and a charge of 2 x 10 -6 C is placed next to one of the two parallel plates 10 cm apart with a 2000 N/C electric field intensity. A) What is the acceleration that the particle gets because of the force due to the electric field between the plates? B) What is the speed of the particle at the other plate?

 Problem #9 Two parallel plates, separated by a distance of 10 cm have an electric field of 5000 N/C. If a 4 x 10 -6 C charge with a mass of 5 x 10 -15 kg is placed next to one plate, A) What will be the acceleration of the charge? B) If it starts from rest, what will be the speed of the charge at the other plate?
Problem #9 Two parallel plates, separated by a distance of 10 cm have an electric field of 5000 N/C. If a 4 x 10 -6 C charge with a mass of 5 x 10 -15 kg is placed next to one plate, A) What will be the acceleration of the charge? B) If it starts from rest, what will be the speed of the charge at the other plate?

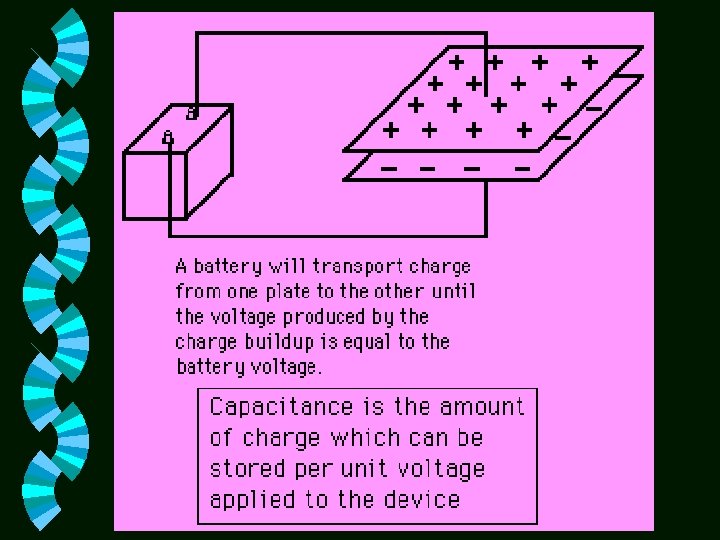
 Capacitor is a device designed to store electric charge. A typical design of a capacitor consists of two parallel plates (metal) separated by a distance d. Plates are connected to a battery. Electrons leave one plate giving it a +Q charge, transferred through the battery and to the other plate giving it a –Q charge. This charge transfer stops when the potential difference across the plates equals the potential difference of the battery. Thus the charged capacitor acts as a storehouse of charge and energy that can be reclaimed when needed for a specific application.
Capacitor is a device designed to store electric charge. A typical design of a capacitor consists of two parallel plates (metal) separated by a distance d. Plates are connected to a battery. Electrons leave one plate giving it a +Q charge, transferred through the battery and to the other plate giving it a –Q charge. This charge transfer stops when the potential difference across the plates equals the potential difference of the battery. Thus the charged capacitor acts as a storehouse of charge and energy that can be reclaimed when needed for a specific application.
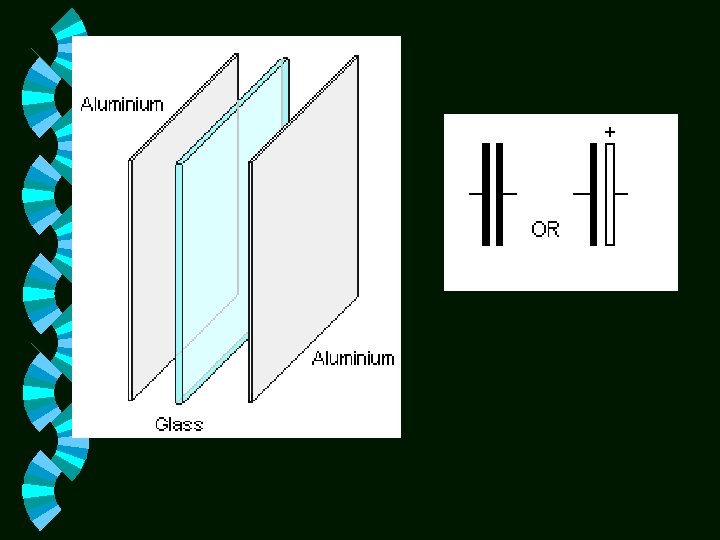
 The capacitance C of a capacitor is defined as the ratio of the magnitude of the charge on either conductor to the magnitude of the potential difference between the conductors. C = Capacitance (Farad) (F) Q = Charge (Coulumb) (C) V = Potential Difference (Volts)(V)
The capacitance C of a capacitor is defined as the ratio of the magnitude of the charge on either conductor to the magnitude of the potential difference between the conductors. C = Capacitance (Farad) (F) Q = Charge (Coulumb) (C) V = Potential Difference (Volts)(V)
 Problem #10 Both 3. 3 x 10 -6 F and 6. 8 x 10 -6 F capacitor are connected across a 15 V battery. Which capacitor has a greater charge? Thus 6. 8 x 10 -6 F has a greater charge.
Problem #10 Both 3. 3 x 10 -6 F and 6. 8 x 10 -6 F capacitor are connected across a 15 V battery. Which capacitor has a greater charge? Thus 6. 8 x 10 -6 F has a greater charge.
 BATTERIES Electrons collect on the negative terminal of the battery. If you connect a wire between the negative and positive terminals, the electrons will flow from the negative to the positive terminal as fast as they can (and wear out the battery very quickly -- this also tends to be dangerous, especially with large batteries, so it is not something you want to be doing). Normally, you connect some type of load to the battery using the wire. The load might be something like a light bulb, a motor or an electronic circuit like a radio.
BATTERIES Electrons collect on the negative terminal of the battery. If you connect a wire between the negative and positive terminals, the electrons will flow from the negative to the positive terminal as fast as they can (and wear out the battery very quickly -- this also tends to be dangerous, especially with large batteries, so it is not something you want to be doing). Normally, you connect some type of load to the battery using the wire. The load might be something like a light bulb, a motor or an electronic circuit like a radio.
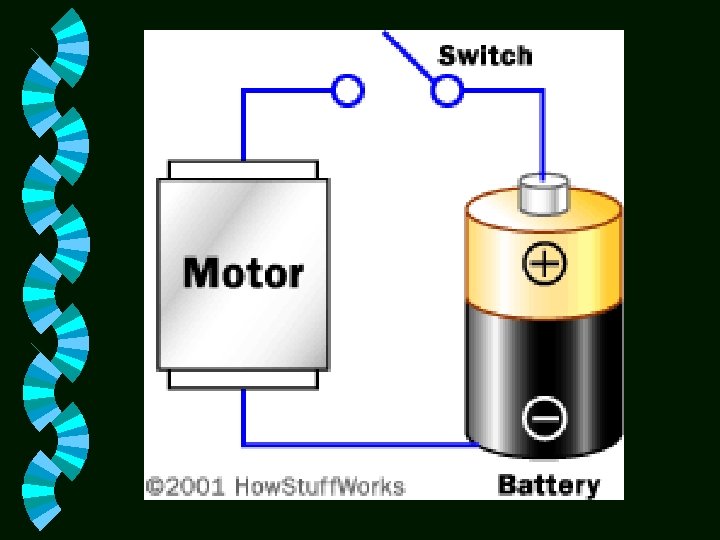
 Inside the battery itself, a chemical reaction produces the electrons. The speed of electron production by this chemical reaction (the battery's internal resistance) controls how many electrons can flow between the terminals. Electrons flow from the battery into a wire, and must travel from the negative to the positive terminal for the chemical reaction to take place. That is why a battery can sit on a shelf for a year and still have plenty of power -- unless electrons are flowing from the negative to the positive terminal, the chemical reaction does not take place. Once you connect a wire, the reaction starts. The first battery was created by Alessandro Volta in 1800. The voltaic pile was made by alternating layers of zinc, blotting paper soaked in salt water, and silver. This arrangement was known as a voltaic pile. The top and bottom layers of the pile must be different metals, as shown. If you attach a wire to the top and bottom of the pile, you can measure a voltage and a current from the pile. The pile can be stacked as high as you like, and each layer will increase the voltage by a fixed amount.
Inside the battery itself, a chemical reaction produces the electrons. The speed of electron production by this chemical reaction (the battery's internal resistance) controls how many electrons can flow between the terminals. Electrons flow from the battery into a wire, and must travel from the negative to the positive terminal for the chemical reaction to take place. That is why a battery can sit on a shelf for a year and still have plenty of power -- unless electrons are flowing from the negative to the positive terminal, the chemical reaction does not take place. Once you connect a wire, the reaction starts. The first battery was created by Alessandro Volta in 1800. The voltaic pile was made by alternating layers of zinc, blotting paper soaked in salt water, and silver. This arrangement was known as a voltaic pile. The top and bottom layers of the pile must be different metals, as shown. If you attach a wire to the top and bottom of the pile, you can measure a voltage and a current from the pile. The pile can be stacked as high as you like, and each layer will increase the voltage by a fixed amount.


