bdb57cbf7366c232c848c4ffb8e85580.ppt
- Количество слайдов: 36

Chapter 16 Review Coulomb’s Law and Electric Fields Objectives • To study quantitatively the nature of forces between electric charges • To develop the concept of the electric field as a transmitter of electric force • To learn how work is done and potential energy is stored in an electric field • To learn how to use electric fields to control and direct the motion of electric charges
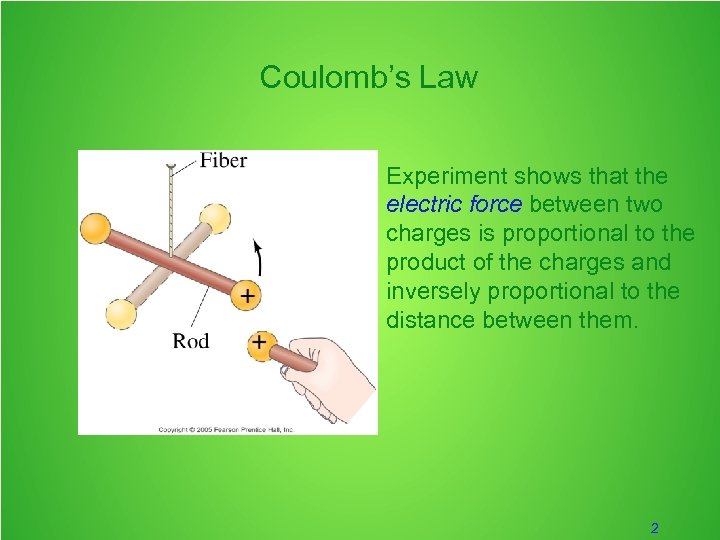
Coulomb’s Law Experiment shows that the electric force between two charges is proportional to the product of the charges and inversely proportional to the distance between them. 2

Coulomb’s Law Coulomb’s law: Where Q 1 and Q 2 are the amount of charge and k is a proportionality constant Charges produced by rubbing ordinary objects (such as a comb or a plastic ruler) are typically around a microcoulomb or less: 3

Coulomb’s Law The magnitude of the charge of an electron, on the other hand, has been determined to be about 1. 602 x 10 -19 C, and its sign is negative. This is the smallest known charge, and because of its fundamental nature, it is given the symbol e and is often referred to as the elementary charge: Example: How many electrons make up a charge of -30. 0 micro coulombs ( C)? N = Q/e = (-30 x 10 -6 C)/ (-1. 60 x 10 -19 C/electrons) = 1. 88 x 1014 electrons What is the mass of 1. 88 x 1014 electrons? Mass = (9. 11 x 10 -31 kg)(1. 88 x 1014 electrons) = 1. 71 x 10 -16 kg 4

Coulomb’s Law The charges carried by the proton and electron are equal in size. However, the mass of the proton is 2000 times the mass of the electron. 5

Coulomb’s Law Double one of the charges Change sign of one of the charges force stays the same Double the distance between charges force changes direction Change sign of both charges force doubles force four times weaker Double both charges force four times stronger 6

Coulomb’s Law vs. Law of Universal Gravitation F = k. Q 1 Q 2/r 2 vs. F=GM 1 M 2/r 2 Both are inverse square laws F 1/r 2 Both have a proportionality to a product of each body-mass for gravity, electric charge for electricity. A major difference is that gravity is always an of electrical force vs. force, whereas the Comparison attractive Gravitational force #1 electric force can be wither attractive or Comparison of electrical force vs. Gravitational Force #2 repulsive. 7 Electrical Force is stronger than

Solving Problems involving Coulomb’s Law Sample problem Find the force between two positive 1. 0 C charges when they are 1000 m apart? Solution q 1=q 2 = 1. 0 C r = 1000 m F = kq 1 q 2/r 2 where k = 9. 0 x 109 Nm 2/C 2 After substitution, F = 9. 0 x 103 N 8

Solving Problems involving Coulomb’s Law Sample problem What is the magnitude of the electric force of attraction between an iron nucleus (q = +26 e) and its innermost electron if the distance between them is 1. 5 x 10 -12 m? Solution F = kq 1 q 2/r 2 where k = 9. 0 x 109 Nm 2/C 2 F = (9. 0 x 109 Nm 2/C 2)(26)(1. 6 x 10 -19 C)(-1. 6 x 10 -19 C)/ (1. 5 x 10 -12 m)2 = -2. 7 x 10 -3 N 9

Solving Problems involving Coulomb’s Law Sample problem What is the repulsive electrical force between two protons in a nucleus that are 5. 0 x 10 -15 m apart from each other? Solution F = kq 1 q 2/r 2 where k = 9. 0 x 109 Nm 2/C 2 F = (9. 0 x 109 Nm 2/C 2)(1. 6 x 10 -19 C)/ (5. 0 x 10 -15 m)2 = 9. 2 N 10

Solving Problems involving Coulomb’s Law AD D VA CE NC Sample problem AN ED DV A Two charged balls are 20. 0 cm apart. They are moved, and the force on each of them is found to have been tripled. How far apart are they now? Solution Let F 1 = kq 1 q 2/r 12 and F 2 = kq 1 q 2/r 22 where F 2 = 3 F 1 F 2/F 1 = r 12 /r 22 3= [(20. 0 cm)/r 2]2, which gives r 2 = 11. 5 cm 11

The Electric Field In physics, the space surrounding an electric charge has a property called an electric field. This electric field exerts a force on other electrically charged objects. The concept of an electric field was introduced by Michael Faraday. The electric field is a vector field with SI units of newtons per coulomb (N C− 1) or, equivalently, volts per meter. The strength of the field at a given point is defined as the force that would be exerted on a positive test charge of +1 coulomb placed at that point; the direction of the field is given by the direction of that force. Michael Faraday (1791 -1867) 12
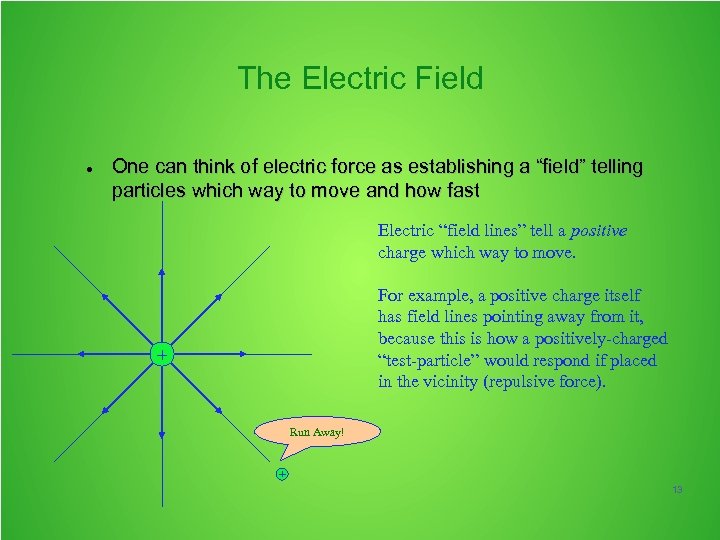
The Electric Field One can think of electric force as establishing a “field” telling particles which way to move and how fast Electric “field lines” tell a positive charge which way to move. For example, a positive charge itself has field lines pointing away from it, because this is how a positively-charged “test-particle” would respond if placed in the vicinity (repulsive force). + Run Away! + 13

The Electric Field The direction of the electric field is always directed in the direction that a positive test charge would be pushed or pulled if placed in the space surrounding the source charge + + 14

The Electric Field Measuring an electric field is a quite simple process involving a test charge. To measure the strength of an electric field, first a test charge must be placed in its vicinity, then calculate the force the test charge “feels”. The resulting number is the strength of the electric field. This process is simplified into the following equation In this equation, F is the magnitude of the force, as found by using Coulomb's Law, q is the magnitude of the test charge. The resulting electric strength is measured in Newton’s per a Coulomb. 15

Electric Field vs. Gravitational Field Right now you are experiencing a uniform gravitational field: it has a magnitude of 9. 8 m/s 2 and points straight down. If you threw a mass through the air, you know it would follow a parabolic path because of gravity. You could determine when and where the object would land by doing a projectile motion analysis, separating everything into x and y components. The horizontal acceleration is zero, and the vertical acceleration is g. We know this because a free-body diagram shows only mg, acting vertically, and applying Newton's second law tells us that mg = ma, so a = g. You can do the same thing with charges in a uniform electric field. If you throw a charge into a uniform electric field (same magnitude and direction everywhere), it would also follow a parabolic path. We're going to neglect gravity; the parabola comes from the constant force experienced by the charge in the electric field. Again, you could determine when and where the charge would land by doing a projectile motion analysis. The acceleration is again zero in one direction and constant in the other. The value of the acceleration can be found by drawing a free-body diagram (one force, F = q. E) and applying Newton's second law. This says: q. E = ma, so the acceleration is a = q. E / m. The one big difference between gravity and electricity is that m, the mass, is always positive, while q, the charge, can be positive, zero, or negative. 16

The Electric Field Sample Problem A positive charge of 1. 0 x 10 -5 C experiences a force of 0. 30 N when located at a certain point. What is the electric field intensity at that point? Solution E=F/q = 0. 30 N / 1. 0 x 10 -5 C = 3. 0 x 104 N/C 17

The Electric Field Sample Problem A test charge experiences a force of 0. 20 N on it when it is placed in an electric field intensity of 4. 5 x 105 N/C. What is the magnitude of the charge? Solution q=F/E = 0. 20 N / 4. 5 x 105 N/C = 4. 4 x 10 -7 C 18

The Electric Field Sample Problem A positive charge of 10 -5 C experiences a force of 0. 2 N when located at a certain point in an electric field. What is the electric field strength at that point? Solution F= 0. 2 N q=10 -5 C E= F/q = 0. 2 N/10 -5 C = 2 x 104 N/C 19

Measuring Potential Difference (Voltage) Electric Strength can also be defined in units of work and energy. This alternative way of measuring the strength of an electric field entails finding the potential difference, which exits between any two points. To visualizing this difference picture an electric field, then trying to force a test charge in between two points, if the test charge is repelled, we have to do work to push it into place. This process is also simplified into the formula In this formula, W is work, q is the magnitude of charge, and V is voltage or potential difference. 20

Measuring Potential Difference (Voltage) Sample Problem It takes 5. 0 x 10 -3 J of work to move a positive charge of 2. 5 x 10 -4 C from point X to point Y on an electric field. What is the difference of Potential between X and Y? Solution W= 5. 0 x 10 -3 J q = +2. 5 x 10 -4 C V = W/q = 5. 0 x 10 -3 J/2. 5 x 10 -4 C = 20 J/C = 20 volts 21

Electronvolt The joule is too large a unit for measuring the work done on moving elementary charges, such as electrons, protons, or the small charges in ions. For this purpose, the electron volt is a more convenient unit of energy or work. An electron volt is the work done in moving an electron or other body having a unit of elementary charge through a difference of potential of one volt. Thus, 1 e. V = 1. 60 x 10 -19 J 22

Electronvolt Sample Problem The difference of potential between point X and point Y of an electric field is 100 volts. (a) How much work done in electronvolts is done by the electric field in moving a free electron from point X and Y. (b) What happens to this work? (c) What is this work in Joules (a) V = 100 V q = +1 electron charge W= 100 volts and 1 electron’s charge = 100 e. V (b) This work is used to accelerate the proton. It is converted into the KE gained by the proton on moving from point X to Y. © 1 ev = 1. 60 x 10 -19 J, so… 100 e. V = 1. 6 x 10 -17 J 23

Electrical Potential Energy In expressing the gravitational potential energy of a body, we learned that a base level such as the surface of the earth must be arbitrarily selected as the level corresponding to zero PE. Similarly, in expressing the PE of a charge in a an electric field, a position of charge corresponding to the base or zero potential energy must first be selected. A charge in the electric field of a point charge is said to have zero PE when it is at an infinite distance from the point charge. This is expressed as: U = K (q 1 q 2)/r 24

Electrical Potential Energy Sample Problem Assuming that a hydrogen atom consists of one electron and one proton separated by a distance of 5. 3 x 10 -11 m, what is the PE of the electron in the field of the proton? Solution U = K (qprotonqelectron)/r = -4. 3 x 10 -18 Nm or J Note that the PE is negative because the charges are opposite and attract each other. 25

Measuring Electric Charge The quantity of charge (q) on an object is related to the (unbalanced) number of electrons that have been either gained or lost by the object. The unit of charge is the coulomb (C). The charge on one electron is the smallest charge known to exist independently and has the value of 1. 60 x 10 -19 coulomb. This value of the electron charge is known as the fundamental charge, e = 1. 60 x 1019 C. Therefore every electron has a charge of -e and every proton (or positive charge due to the loss of one electron) has a charge of +e. A rubber balloon becomes negatively charged after you rub the balloon with a wool cloth. The quantity of charge due to the excess electrons on the balloon can be found according to the following general relationship: Quantity of (positive or negative) charge, q = (number of electrons, Ne) x (fundamental (electron) charge, +e or - e) So, q = (Ne)(e) 26
Measuring Electric Charge Sample Problem What is the charge of 1000 electrons? Q = (Ne)(e) = 1000 (-1. 6 x 10 -19 C) = - 1. 6 x 10 -16 C 27

Rye High School: Physics Field Lines The electric field can be represented by field lines. These lines start on a positive charge and end on a negative charge. At locations where electric field lines meet the surface of an object, the lines are perpendicular to the surface. 28
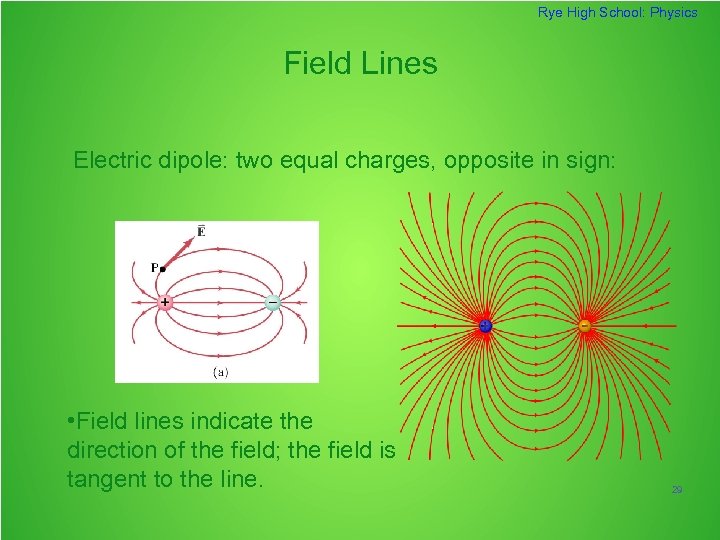
Rye High School: Physics Field Lines Electric dipole: two equal charges, opposite in sign: • Field lines indicate the direction of the field; the field is tangent to the line. 29

Rye High School: Physics Field Lines The number of field lines starting (ending) on a positive (negative) charge is proportional to the magnitude of the charge. Electric field lines never cross each other. The electric field is stronger where the field lines are closer together. 30
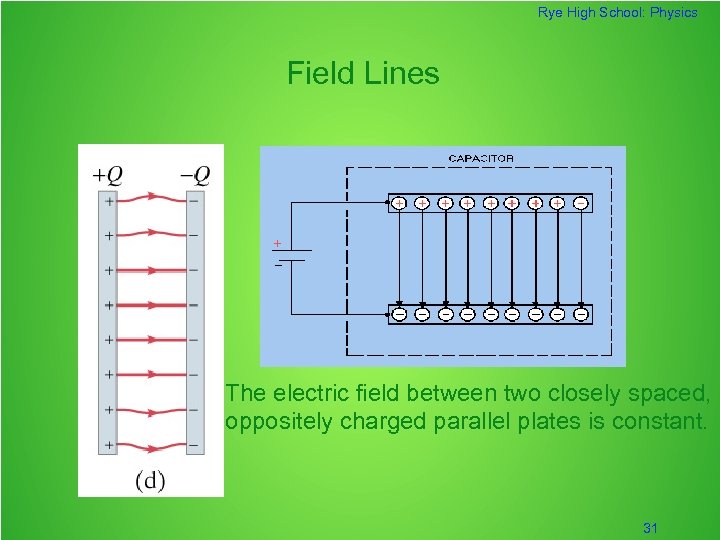
Rye High School: Physics Field Lines The electric field between two closely spaced, oppositely charged parallel plates is constant. 31

Rye High School: Physics Field Lines Summary of Field lines Around Charges • The magnitude of the field is proportional to the density of the lines. • Field lines start on positive charges and end on negative charges • Field lines indicate the direction of the field; the field is tangent to the line. • The electric field between two closely spaced, oppositely charged parallel plates is constant. • At locations where electric field lines meet the surface of an object, the lines are perpendicular to the surface. • Electric field lines never cross each other. 32

Rye High School: Physics Millikan’s Oil Drop Experiment One important application of the uniform electric field between two parallel plates is the measurement of charge of an electron. This was determined by American physicist Robert A Millikan in 1909 Millikan’s experiment showed that charge is quantized. This means that an object can only have a charge with a magnitude that is some integral multiple of the charge of the electron (1. 6 x 10 -19 C). 33

Rye High School: Physics Millikan’s Oil Drop Experiment Sample Problem In a Millikan oil drop experiment, a drop has been found to weigh 1. 9 x 10 -14 N. When the electric field is 4. 0 x 104 N/C, the drop is suspended motionless. (a) what is the charge on the drop? (b) If the upper plate is positive, how many excess electrons does the oil drop have? Solution (a) When balanced, Felectric = F gravity Thus, q. E=mg solving for q, the charge will be q=mg/E = 1. 9 x 10 -14 N/4. 0 x 104 N/C = 4. 8 x 10 -19 C (b) Determine the number of electrons by n=q/e n=4. 4 x 10 -19 C/1. 6 x 10 -19 C/electron = 3 electrons 34

Rye High School: Physics Millikan’s Oil Drop Experiment Sample Problem A positively charged oil drop weighs 6. 4 x 10 -13 N. An electric field of 4. 0 x 106 N/C suspends the drop. (a) What is the charge on the drop? (b) How many electrons is the drop missing? Solution (a)Q=F/E = 6. 4 x 10 -13 N/ 4. 5 x 106 N/C = 1. 6 x 10 -19 C (b) N = Q/e = 1. 6 x 10 -19 C/electron = 1 electron 35

Rye High School: Physics Summary • • Coulomb’s Law: F = k. Q 1 Q 2/r 2 Units of Coulomb’s Law is the Newton. Electric Field: E = F/Q Units of Electric Field are Newtons per Coulomb Potential Difference: V = W/Q Units of Potential difference is Joules per Coulomb Work (W) = QV The work done in moving an electric charge can be expressed in joules or electron volts (e. V). • One electron volt is equal to 1. 60 x 10 -19 joule • Potential Energy of a charge: U = k. Q 1 Q 2/r 36
bdb57cbf7366c232c848c4ffb8e85580.ppt