Chapter 16 Planning Methods 1 Chapter 16

Chapter 16 Planning Methods 1

Chapter 16 Contents (1) l l l STRIPS Implementation Partial Order Planning The Principle of Least Commitment Propositional Planning SAT Planning 2

Chapter 16 Contents (2) l l l l Planning Graphs Graph. Plan ADL and PDDL Probabilistic Planning Dynamic World Planning Case-Based Planning Scheduling 3

STRIPS (1) l l l Stanford Research Institute Problem Solver. An operator based planning system. STRIPS uses wffs in FOPC to describe the world. For example: STRIPS was designed to enable a planner to devise plans for a robot which is to solve problems in the blocks world. 4

STRIPS (2) l STRIPS defines operators as in the following rule schemata: Precondition: Delete: Add: l l AT(r, x) Λ AT(o, x) AT(r, x) AT(o, x) AT(r, y) AT(o, y) The preconditions specify what must be true for the operator to be applied. The delete and add lists specify the changes that will take place after the operator is applied. 5

STRIPS Implementation STRIPS uses resolution and meansends analysis to devise plans: l The goal is negated, and the rule schemata are instantiated with objects from the real world. l If the resolution fails, then the goal has been achieved. l Otherwise, a plan must be devised. l 6

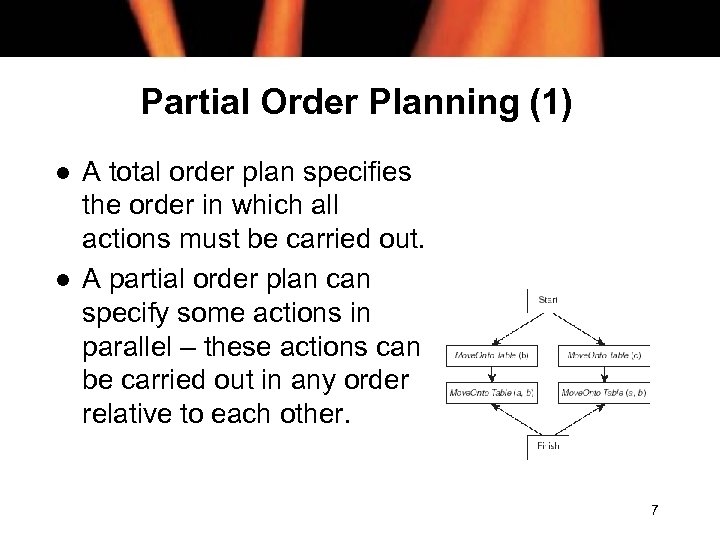Partial Order Planning (1) l l A total order plan specifies the order in which all actions must be carried out. A partial order plan can specify some actions in parallel – these actions can be carried out in any order relative to each other. 7

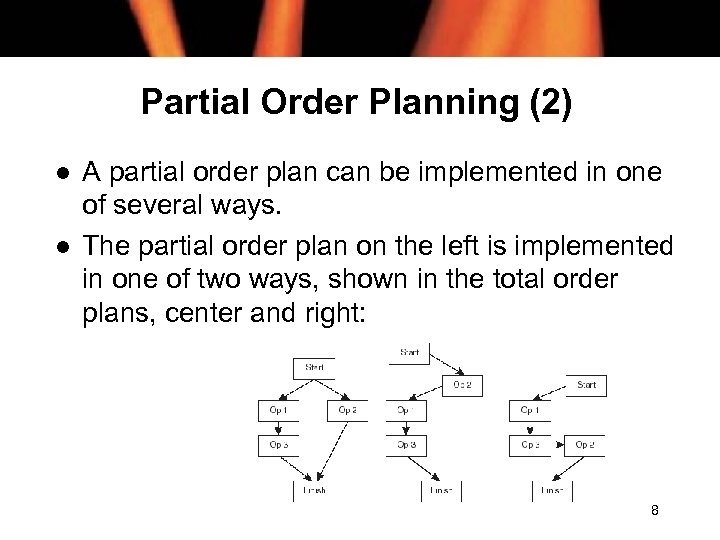Partial Order Planning (2) l l A partial order plan can be implemented in one of several ways. The partial order plan on the left is implemented in one of two ways, shown in the total order plans, center and right: 8

The Principle of Least Commitment l l l In building a plan there will be some variables and objects that can be ignored, as they are superfluous to the goal of the plan. Some variables do not need to be instantiated – for example it is preferable, where possible, to use Move. Onto (a, y) than to use Move. Onto (a, b). This is the Principle of Least Commitment. 9

Propositional Planning (1) Any STRIPS plan can be expressed in propositional logic. l This will often involve increasing the number of variables. l 10

Propositional Planning (2) l l l Any STRIPS plan can be expressed in propositional logic. This will often involve increasing the number of variables. For example: Clear (x) On (x, y) These predicates can be represented as propositions: X 1 is equivalent to Clear (A) X 2 is equivalent to Clear (B) X 3 is equivalent to On (A, B) X 4 is equivalent to On (B, A) 11

Propositional Planning (3) l l States can be represented as an assignment of truth values to the propositions: X 1 Λ ¬X 2 Λ X 3 Λ ¬ X 4 This state can be represented in STRIPS notation as: Clear (A) Λ ¬Clear (B) Λ On (A, B) Λ ¬On (B, A) l The following sentence represents all states in which A is clear and B is not clear: X 1 Λ ¬X 2 12

Propositional Planning (4) l l l Actions can also be represented as the preconditions and the results of the action. We use the notation ¬X 1’ to indicate that X 1’ is no longer true after the action. Hence, an action might be: X 1 Λ X 2 Λ ¬X 3 Λ ¬X 4 Λ X 1’ Λ ¬X 2’ Λ X 3’ Λ ¬X 4’ This action is Move. Onto (A, B). This is a simple example, but propositional planning can lead to very complex expressions being used. The advantage of using propositional planning is that automated systems can be built to manipulate the plans. 13

SAT Planning l l l The satisfiability problem, of determining whether a given propositional logic sentence is satisfiable or not, is NPComplete. A number of efficient methods have been developed for devising plans by determining the satisfiability of propositional logic expressions. Methods are either systematic, which involve checking all possible assignments of truth values, or stochastic. 14

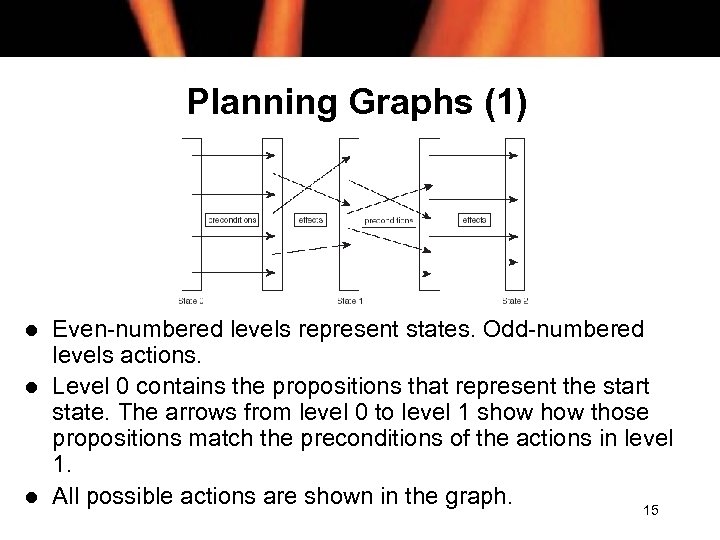Planning Graphs (1) l l l Even-numbered levels represent states. Odd-numbered levels actions. Level 0 contains the propositions that represent the start state. The arrows from level 0 to level 1 show those propositions match the preconditions of the actions in level 1. All possible actions are shown in the graph. 15

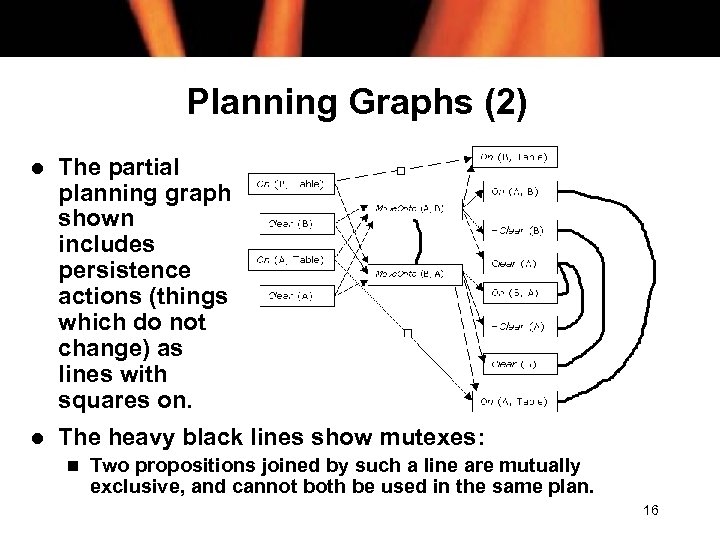Planning Graphs (2) l The partial planning graph shown includes persistence actions (things which do not change) as lines with squares on. l The heavy black lines show mutexes: n Two propositions joined by such a line are mutually exclusive, and cannot both be used in the same plan. 16

Planning Graphs (3) l l l The planning graph for even a simple problem can be extremely complex. By producing a complete planning graph for a problem, it can be determined whether a plan is possible, and the plan itself can also be derived. Algorithms such as Graph. Plan can be used to extract the plan. 17

Graph. Plan l l Problems are expressed in STRIPS notation. Graph. Plan iteratively builds a planning graph, starting from the initial state and working towards the goal state. All applicable operators are applied at each level to produce the next level. When the propositions necessary for the goal are included in the current level, and they are not mutex, a possible solution may have been reached. 18

ADL l l Another method for representing planning problems. ADL – Action Description Language: More expressive than STRIPS. n Allows quantified expressions such as: x. P(x) Λ ¬ Q(x) n Preconditions can include disjunctions. n Allows conditional effects – effects of actions that are dependent on other factors. n 19

Probabilistic Planning Thus far we have assumed that all actions are deterministic. l In fact, some actions are nondeterministic – their effects can vary. l It is possible to extend situation calculus to deal with nondeterministic actions. l 20

Dynamic World Planning l l l Our discussion so far has assumed the world is static. In fact, the world is dynamic – things outside of the control of the planner change. Execution monitoring is used to monitor the execution of plans: n l If something changes during execution, replanning may be necessary. Another approach is conditional planning – this includes every possible outcome in the plan. 21

Case-Based Planning l l Case-based planning involves storing each plan that is devised. Plans (and partial plans) can be re-used later to solve other, similar problems. Example: CHEF. A system that is used to devise recipes for Chinese food given a set of ingredients. If presented with a set of ingredients it has not seen before, it is able to use similar sets of ingredients it has seen before to devise a new recipe. 22

Scheduling l l Scheduling is like planning, but also takes into account the length of time each action takes to execute. Job-shop scheduling involves allocating machinery to a set of tasks. The scheduler plans when each task will start, and how long it will take. Scheduling can be treated as planning with constraints, where the constraints specify how long tasks will take. 23