208201d8b63cb0f39d7a5b96ad768527.ppt
- Количество слайдов: 26

CHAPTER 16: CAPITAL STRUCTURE – BASIC CONCEPTS Topics: – 16. 1 -16. 2 – 16. 3 -16. 4 The Basics Capital Structure in Perfect Markets • Modigliani and Miller: Proposition I (No Taxes) • Modigliani and Miller: Proposition II (No Taxes) 1
Nobel Price Winners in your Textbook • Harry Markowitz (1990) • William Sharpe (1990) – CAPM • Merton Miller (1990) • Franco Modigliani (1985) – Capital structure • To come – Myron Scholes (1997) – Robert Merton (1997) • Option pricing 2

16. 1 The Definition • • What is capital structure? The pie Firm value V = B (market value of debt) + S (market value of equity) A capital structure ratio: Debtequity ratio: B/S • Two Questions in Capital Structure 1. What happens to the cost of various sources of funds when the capital structure is changed? 2. Is there an optimal capital structure? 3

Cost of Equity Capital Review • CAPM: Cost of equity = r. S = rf+ β [E(r. M) − rf] – β= Cov(rs, , r. M) / Var(r. M) • Other sources of funds: what if there is leverage? – Cost of debt = r. B = expected return on firm’s debt, i. e. , the rate of interest paid – The weighted average cost of capital (WACC) is given by • Note that for now we ignore the tax deductibility of interest payments • Read over chapters 11 and 13 to review these concepts 4

16. 2 Management objective revisited • Objective of management: Maximizing S • However, as long as there is no costs of bankruptcy, maximizing S is equivalent to maximizing V An example: Firm has 10, 000 shares. Share price = $25. Debt has a market value of $100, 000. V = B + S = 100, 000 + 10, 000 * 25 = 350, 000 Now suppose firm borrows another $50, 000 and pays it immediately as a special dividend. B = 100, 000 + 50, 000 = 150, 000 What would be shareholder gain/loss if firm value changes? 5
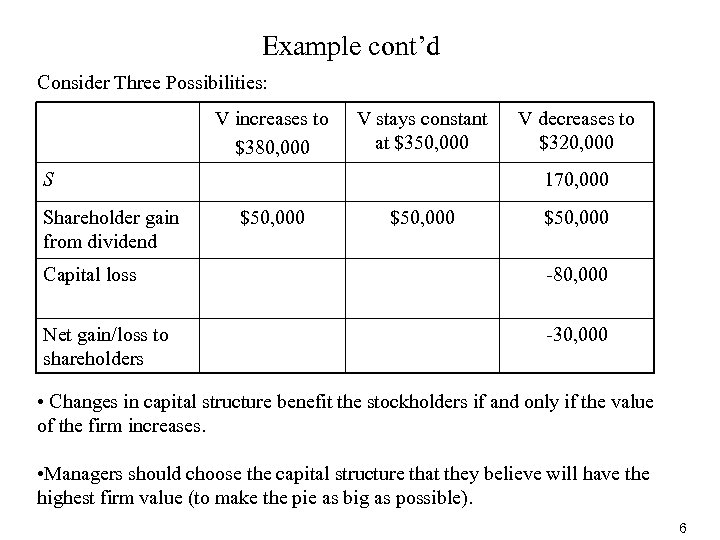
Example cont’d Consider Three Possibilities: V increases to $380, 000 V stays constant at $350, 000 S Shareholder gain from dividend V decreases to $320, 000 170, 000 $50, 000 Capital loss -80, 000 Net gain/loss to shareholders -30, 000 • Changes in capital structure benefit the stockholders if and only if the value of the firm increases. • Managers should choose the capital structure that they believe will have the highest firm value (to make the pie as big as possible). 6

What is the optimal capital structure, if any, that maximizes firm value? • Assume Perfect Capital Markets (PCM): – – – Information is free and available to everyone on an equal basis. No transaction costs No taxes No costs of bankruptcy Firms and investors can borrow / lend at the same rate • MM Proposition I (no taxes): The market value of any firm is independent of its capital structure. – Let VU be the value of an “unlevered” firm (i. e. , all equity financing), and VL be the value of an otherwise identical “levered” firm (i. e. some debt financing): VL = VU. 7

16. 3 Proof of MM Proposition I (No taxes): VL = VU • Assume that all cash flows are perpetuities (just to make the calculations easier). Let X be the identical cash flow stream generated by each firm (i. e. U and L); VU = SU be the value of the unlevered firm, and VL = SL + BL be the value of the levered firm. • Consider an investor who owns some fraction α (e. g. 5%) of the shares of U: • This investor can get the same return by investing in L: • If Vu > VL the investor would not buy any shares in U since the same return is available on a similar investment in L 8

Proof cont’d • Consider an investor who owns α of L’s equity • This investor can get the same return by investing in U and borrowing on personal account: • If VL > VU the investor would not buy any shares in L since the same return is available on a smaller investment in U 9

Proof cont’d • We have shown that no one would buy shares in U if VU > VL and that no one would buy shares if VL > VU • Therefore VU = VL is the only solution consistent with market equilibrium • The same arguments apply to more complicated capital structures • The same arguments apply if cash flows are not perpetuities and/or not constant. 10

Some observations • MM’s result is based on a no-arbitrage argument: if two investments give the same future returns, they must cost the same today • A key (implicit) assumption is that individuals can borrow as cheaply as corporations – One way to do this is through buying stock on margin – With a margin purchase, the broker lends the investor a portion of the cost (e. g. , to buy $10, 000 of stock on 40% margin, put up $6, 000 of your own money and borrow $4, 000 from the broker) – Since the broker holds the stock as collateral, brokers generally charge relatively low rates of interest – Firms, on the other hand, often borrow using illiquid assets as collateral (and get charged higher rates) 11

Example #1 • Given VU = $100 m, X = $10 m, r = 5%, BL = $50 m, then MM Proposition I implies SL = 50 M • Suppose SL = $40 m • Suppose SL = $60 M 12

Example #2: Uncertain cash flows Consider an all-equity firm, Trans Can, that is considering going into debt. (Maybe some of the original shareholders want to cash out. ) Current Assets $8, 000 Debt $0 Equity $8, 000 Debt/Equity ratio Interest rate n/a Shares outstanding Share price $20 0 400 Proposed (50% debt) $8, 000 $4, 000 1 10% 200 $20 13
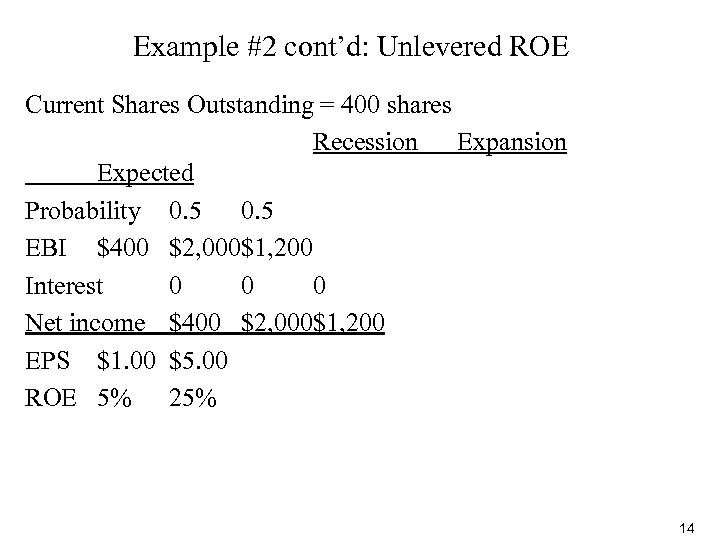
Example #2 cont’d: Unlevered ROE Current Shares Outstanding = 400 shares Recession Expansion Expected Probability 0. 5 EBI $400 $2, 000$1, 200 Interest 0 0 0 Net income $400 $2, 000$1, 200 EPS $1. 00 $5. 00 ROE 5% 25% 14
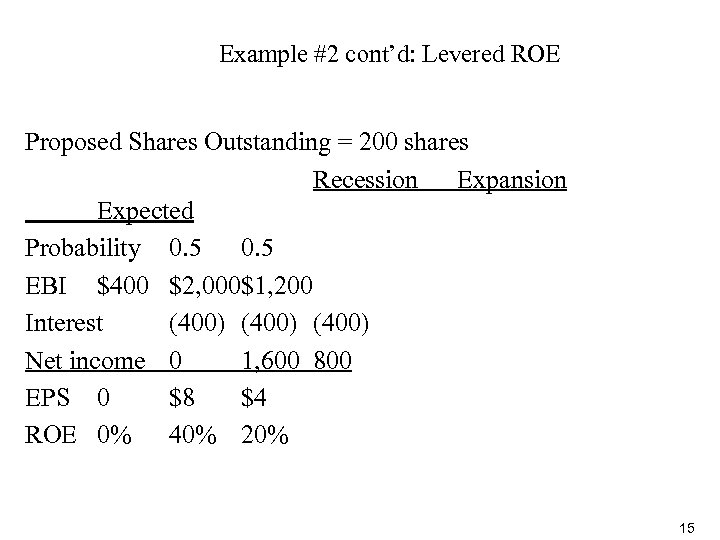
Example #2 cont’d: Levered ROE Proposed Shares Outstanding = 200 shares Recession Expansion Expected Probability 0. 5 EBI $400 $2, 000$1, 200 Interest (400) Net income 0 1, 600 800 EPS 0 $8 $4 ROE 0% 40% 20% 15

Example #2 cont’d • Since the expected ROE is higher under 50% debt, should the firm switch to this capital structure? • Not only have expected returns increased, but so has risk • The MM argument is that it doesn’t matter, because investors can effectively create the payoffs from the alternative capital structure themselves (“homemade leverage”) 16

Example #2 cont’d: Replicate the higher EPS with only an unlevered firm and borrowing: homemade leverage Assume that you buy 200 shares of unlevered firm using $2, 000 of your own money and borrowing the rest $2, 000 at 10% on margin from your broker. Recession Expansion Expected EPS of Unlevered Firm $1 $5 $3 Earnings for 200 shares $600 Less interest on $2000 (200) Net Profits $400 ROE (Net Profits / $2, 000) 20% Same ROE as if we bought into a levered firm! What’s the trick? • Our personal debt equity ratio (personal leverage) is the same as the levered equity – Personal Debt contribution/equity contribution 17
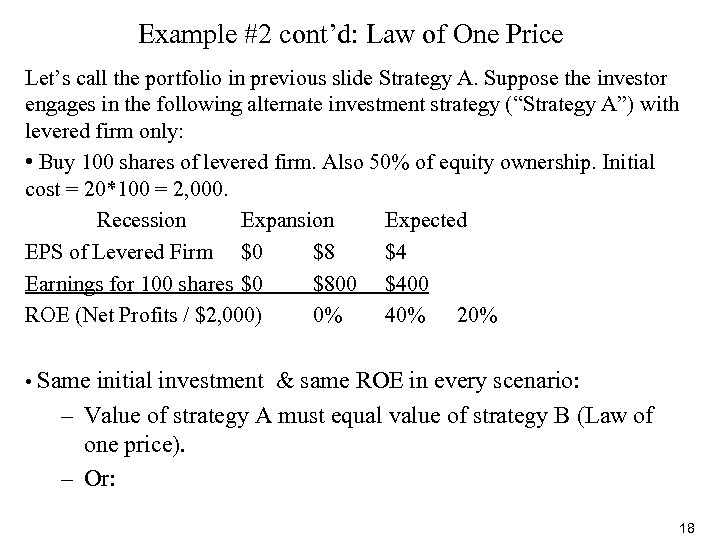
Example #2 cont’d: Law of One Price Let’s call the portfolio in previous slide Strategy A. Suppose the investor engages in the following alternate investment strategy (“Strategy A”) with levered firm only: • Buy 100 shares of levered firm. Also 50% of equity ownership. Initial cost = 20*100 = 2, 000. Recession Expansion Expected EPS of Levered Firm $0 $8 $4 Earnings for 100 shares $0 $800 $400 ROE (Net Profits / $2, 000) 0% 40% 20% • Same initial investment & same ROE in every scenario: – Value of strategy A must equal value of strategy B (Law of one price). – Or: 18

How is no-arbitrage principle used in proving MM? • Arbitrage opportunity, in principle, allows you to: – have non-negative profit in every state of the world with an initial investment of $0. • We’ll show that if VL ≠ VU there exists an arbitrage opportunity. • By Law of One Price the arbitrage opportunity will disappear instantaneously. • Suppose instead PL=21, so that SL = 4, 200 and VL = 8, 200 > VU 19

No arbitrage cont’d • What to do? – Buy low and sell high • We consider a simple occasion where buy and sell involve same percentage of equity – Borrow or lend to make initial investment be zero • Synthetic strategy: (1) Buy low: buy 50% of U’s equity, costs 200 shares * 20 = 4, 000 (2) Sell high: (short) sell 50% of L’s equity, proceeds 100 shares * 21 = 2, 100 (3) Zero initial investment: borrow 1, 900 at 10%. • What’s my payoff? 20

No arbitrage cont’d Cashflow (dividend income) Buy 50% of U (200 sh. ) Short 50% of L (100 sh. ) Borrow 1, 900 at 10% Net Profits ROE (Net Profits /0) Recession Expansion $200 $1000 Expected $600 (400) (190) 10 +∞ At time T, you clear your position by reversing (1) (2) (3) in the previous slide and receive 0 back. • I will make $ in every scenario with zero initial investment. • But everyone else can do it… 21

How does leverage affect shareholder returns? • Note that from previous example that leverage increases the expected return and risk of equity, even if there is no chance of bankruptcy • Recall the weighted average cost of capital formula • MM proposition I implies that the WACC is constant (i. e. , independent of capital structure) • In the previous example: 22

16. 4 MM Proposition II: Cost of equity • Define • Since r 0 = r. WACC , we have • This can be re-arranged to yield MM Proposition II – Leverage increases the risk and return to stockholders 23
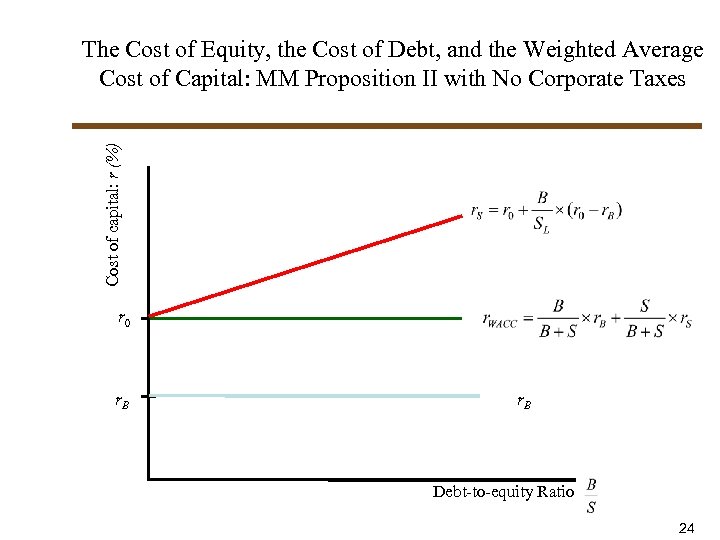
Cost of capital: r (%) The Cost of Equity, the Cost of Debt, and the Weighted Average Cost of Capital: MM Proposition II with No Corporate Taxes r 0 r. B Debt-to-equity Ratio 24

Example #2 cont’d • Cost of equity of unlevered firm r 0 = expected earnings to unlevered firm/unlevered equity = 1200/8000 = 15% rs = Is this right: 25

• Assigned Problems # 16. 2, 3, 4, 6, 8, 10, 11 26
208201d8b63cb0f39d7a5b96ad768527.ppt