CHAPTER 16 Asset Prices and Interest Rates MACROECONOMICS

CHAPTER 16 Asset Prices and Interest Rates MACROECONOMICS and the FINANCIAL SYSTEM N. Gregory Mankiw & Laurence M. Ball © 2011 Worth Publishers, all rights reserved Power. Point® slides by Ron Cronovich

In this chapter, you will learn: § the classical theory of asset prices, which uses present value to determine the price of an asset that provides a stream of payments to its owner. § how asset-price bubbles and crashes work, and examples of both § two ways to measure bond returns/yields § about the relation of bond terms and yields, and how to use this relationship to predict future interest rates CHAPTER 16 Asset Prices and Interest Rates 1

INTRODUCTION: Valuing income streams § Assets provide future income to their owners. § Coupon bonds provide fixed coupon payments until maturity, then face value upon maturity § Stocks pay dividends while owned, then proceeds of the sale when sold § To determine the price of an asset, must figure out the value of these income streams. § To do this, we use the concepts of present value and future value… CHAPTER 16 Asset Prices and Interest Rates 2

Future value § The future value of a dollar today is the number of dollars it will be worth at some future time. § Example: i = interest rate in decimal form = 0. 06 $100 today is worth… $100 x (1+0. 06) = $106. 00 in one year $100 x (1+0. 06)2 = $112. 36 in two years $100 x (1+0. 06)5 = $133. 83 in five years CHAPTER 16 Asset Prices and Interest Rates 3

Future value § Notation: FV = = PV = = n = future value the value of an amount in the future present value the value of the amount in the present number of years in the future § Formula for future value: $FV = $PV x (1 + i )n CHAPTER 16 Asset Prices and Interest Rates 4

Present value § The present value of a dollar in the future is the number of dollars it is worth today. § Divide $FV = $PV x (1 + i )n by (1 + i )n: § Formula for present value: $FV $PV = (1 + i )n § Example: $100 present value of $100 = $94. 64 = 1 + 0. 06 to be received in one year CHAPTER 16 Asset Prices and Interest Rates 5

NOW YOU TRY: Present Value Assume i = 0. 04 for borrowing and saving. What’s the present value of $500 to be received in… a. one year? b. two years? c. twenty years?

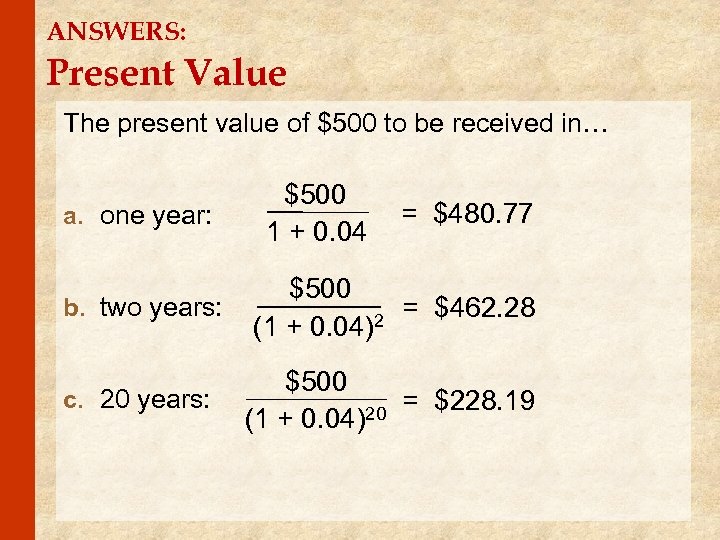ANSWERS: Present Value The present value of $500 to be received in… a. one year: $500 1 + 0. 04 = $480. 77 b. two years: $500 = $462. 28 2 (1 + 0. 04) c. 20 years: $500 = $228. 19 20 (1 + 0. 04)

NOW YOU TRY: Present Values and Interest Rates What is the present value of $500 to be received in two years if the interest rate is: a. i = 0. 04 b. i = 0. 08 c. i = 0. 12

ANSWERS: Present Values and Interest Rates Present value of $500 to be received in two years: a. If i = 0. 04, $500 = $462. 28 2 (1 + 0. 04) b. If i = 0. 08, $500 = $428. 67 2 (1 + 0. 08) c. If i = 0. 12, $500 = $398. 60 2 (1 + 0. 12)

Present values and interest rates § A higher interest rate reduces the present value of future money. § When the interest rate is higher, you don’t need to save as much today to end up with a particular amount in the future. CHAPTER 16 Asset Prices and Interest Rates 10

NOW YOU TRY: Valuing a series of payments § A share of Google stock will pay a dividend of $5 in one year, $8 in two years, and $10 in three years. The interest rate is i = 0. 05. § Find the present value of each payment. § Add them up to get the present value of the series of payments.

NOW YOU TRY: Valuing a series of payments PV of $5 in one year = $5/(1. 05) = $4. 76 PV of $8 in two years = $8/(1. 05)2 = $7. 26 PV of $10 in three years = $10/(1. 05)3 = $8. 64 The PV of the series of payments is the sum of these amounts: $4. 76 + $7. 26 + $8. 64 = $20. 66

Formula for valuing a series of payments § The series of payments is: $X 1 in one year, $X 2 in two years, … $XT in T years § The present value of this payment series equals $X 1 $X 2 $XT $X 3 + + + … + 1 2 3 (1 + i )T (1 + i ) CHAPTER 16 Asset Prices and Interest Rates 13

Payments forever § A perpetuity is a bond that pays interest forever but never matures. § If the payment is $Z each period, the PV equals $Z $Z + + + … = 1 2 3 (1 + i ) i (1 + i ) CHAPTER 16 Asset Prices and Interest Rates 14

Payments that grow forever § The payment is $Z in one year, then grows at rate g forever. § PV of this payment stream equals $Z $Z(1+g)1 $Z(1+g)2 $Z + + +… = 1 3 2 (1 + i ) i –g CHAPTER 16 Asset Prices and Interest Rates 15

The Classical Theory of Asset Prices § Classical theory of asset prices says asset price = p. v. of expected asset income People below p. v. of expected § If asset’s price isdetermine asset values income, using expectations/forecasts everyone will buy, driving the price up. when future income is unknown. § If asset’s price is above p. v. of expected income, current owners will sell, driving the price down. CHAPTER 16 Asset Prices and Interest Rates 16

NOW YOU TRY: Pricing a bond Use the classical theory to determine the price of a Ford Motor Company bond with these characteristics: § Bond matures in 2 years § Face value (paid upon maturity) = $10, 000 § Two coupon payments of $250 paid in 1 and 2 years, respectively § i = 0. 07

ANSWERS: Pricing a bond First, determine PV of each payment: payment present value 1 st coupon $250/(1. 07)1 = $ 233. 64 2 nd coupon $250/(1. 07)2 = $ 218. 36 face value $10, 000/(1. 07)2 = $8, 734. 39 Price of bond equals sum of PV of all payments $9, 186. 39

Formula for price of a coupon bond § Notation: F = face value, C = annual coupon payment, T = years to maturity § Bond price equals CHAPTER 16 Asset Prices and Interest Rates 19

Formula for price of a stock § D 1 = dividend expected in one year, D 2 = dividend expected in two years, etc. § Stock price equals CHAPTER 16 Asset Prices and Interest Rates 20

NOW YOU TRY: Pricing a stock with growing dividends § The interest rate is 5%. § IBM stock pays annual dividends that start at $10 next year and grow 3% every year thereafter. § Find the price of IBM stock.

ANSWERS: Pricing a stock with growing dividends § Use the formula for the present value of a series of payments that grows forever: $Z $Z(1+g)1 $Z(1+g)2 $Z + + +… = 1 3 2 (1 + i ) i –g § Set i = 0. 05, g = 0. 03, and $Z = dividend next year = $10 § Answer: the price of IBM stock equals $10 = $500 0. 05 – 0. 03

The Gordon Growth Model § due to Myron Gordon (1959). § D = dividend next year, g = expected growth rate of dividends, i = interest rate D Stock price = i–g CHAPTER 16 Asset Prices and Interest Rates 23

What determines expectations? § The classical theory assumes rational expectations – people optimally use all available information to forecast future variables like dividends. § Example: auto stocks in a recession § If economy enters a recession, auto sales fall sharply. § People will lower their forecasts of automakers’ future earnings. § Automakers’ stock prices fall. CHAPTER 16 Asset Prices and Interest Rates 24

What is the relevant interest rate? § The more uncertain people are about an asset’s future income, the riskier the asset. § People prefer “safe” future dollars to risky ones, so the interest rate used to price assets must be adjusted for risk. Notation: i safe = safe (risk-free) interest rate = risk premium, a payment that compensates for risk i = i safe + = risk-adjusted interest rate § The riskier the asset, the greater the risk premium. CHAPTER 16 Asset Prices and Interest Rates 25

NOW YOU TRY: Flucations in asset prices 1. In the context of the classical theory, think of an event that would cause a change in the price of Verizon Communications Inc. stock. 2. Would this event also change the price of Verizon Communications Inc. bonds?

ANSWERS: Flucations in asset prices 1. Examples of things that would affect the price of Verizon Communications Inc. stock: § Verizon comes out with a new phone that everybody wants to buy. Expected earnings rise, causing stock price to rise. § An increase in the perceived riskiness of holding communications stocks, which increases the risk premium and risk-adjusted interest rate and lowers Verizon’s stock price. § The safe interest rate rises, reducing the present value of Verizon’s future earnings.

ANSWERS: Flucations in asset prices 2. Would any of these things also change the price of Verizon Communications Inc. bonds? § The bond price will not change in response to news about Verizon’s future earnings, because income bondholders receive is fixed. (Exception: news that leads people to worry Verizon will default will raise the risk premium and risk-adjusted interest rate, causing bond price to fall. ) § The bond price will change in response to a change in the safe interest rate, which alters the present value of future bond income.

Monetary policy and stock prices If the Fed unexpectedly raises the Fed Funds rate, § i safe rises, reducing present value of future dividends and hence stock prices § consumption and investment spending fall, lowering expected earnings and stock prices § risk premiums rise if people are uncertain about how badly companies will be hurt, which increases risk-adjusted interest rate and reduces stock prices § If the Fed’s move was expected, stock prices would have adjusted in advance. CHAPTER 16 Asset Prices and Interest Rates 29

Monetary policy and stock prices § Research by Bernanke and Kuttner: During the sample period 1989 -2002, each 0. 25 percent surprise increase in FF rate caused stock prices to fall 1 percent on average. CHAPTER 16 Asset Prices and Interest Rates 30

DISCUSSION QUESTION: Volatility of stocks vs. bonds § Based on what we’ve learned so far in this chapter, which do you think would be more volatile, stock prices or bond prices? Justify your answer.

Volatility of stock and bond prices § Stock prices tend to be more volatile than bond prices: § both are affected by changes in interest rates § but stock prices are more affected than bond prices by news that changes expected future earnings § What about short-term bonds vs. long-term bonds? CHAPTER 16 Asset Prices and Interest Rates 32

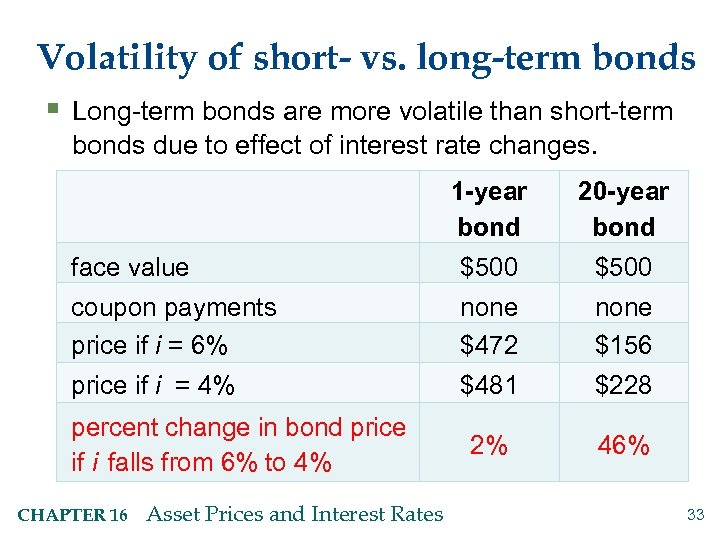Volatility of short- vs. long-term bonds § Long-term bonds are more volatile than short-term bonds due to effect of interest rate changes. 1 -year bond 20 -year bond face value $500 coupon payments price if i = 6% none $472 none $156 price if i = 4% $481 $228 2% 46% percent change in bond price if i falls from 6% to 4% CHAPTER 16 Asset Prices and Interest Rates 33

Asset-price bubbles § Bubble: a rapid increase in asset prices not justified by interest rates or expected income. § If people believe a stock’s price will rise, they will buy the stock, causing the price to rise. § Any asset can experience a bubble, including houses, currencies, precious metals, and even tulip bulbs. CHAPTER 16 Asset Prices and Interest Rates 34

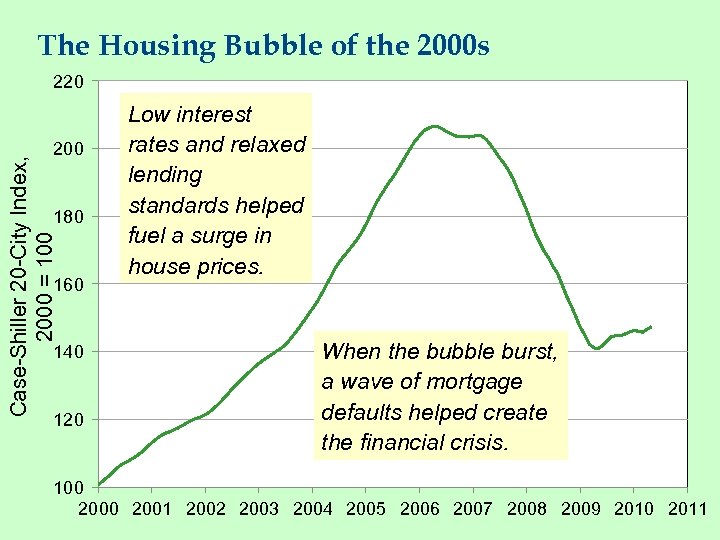The Housing Bubble of the 2000 s 220 Case-Shiller 20 -City Index, 2000 = 100 200 180 160 140 120 Low interest rates and relaxed lending standards helped fuel a surge in house prices. When the bubble burst, a wave of mortgage defaults helped create the financial crisis. 100 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

Using the P/E ratio to identify bubbles § Price-earnings (P/E) ratio: the price of stock divided by earnings per share § Suppose expected earnings are similar to recent earnings. Then, a high P/E means price is high relative to expected earnings. § In the classical theory, this would require falling interest rates. If rates are not falling, must be a bubble. § Problem: expected earnings may be different than recent earnings CHAPTER 16 Asset Prices and Interest Rates 36

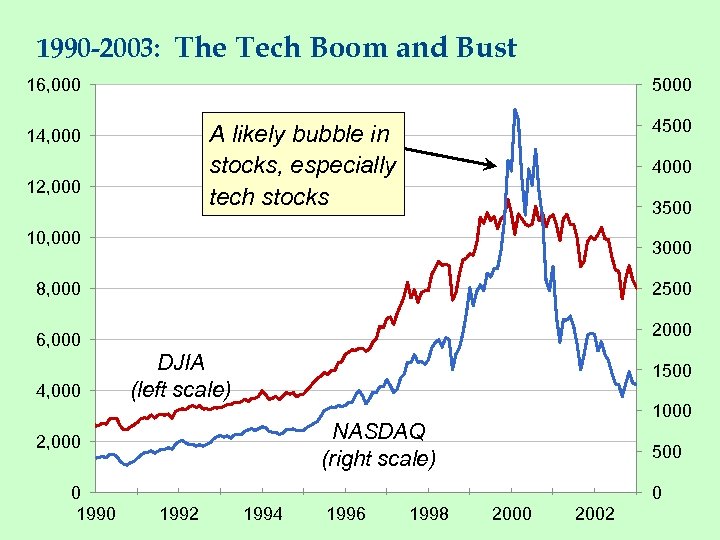1990 -2003: The Tech Boom and Bust 16, 000 5000 4500 A likely bubble in stocks, especially tech stocks 14, 000 12, 000 4000 3500 10, 000 3000 8, 000 2500 2000 6, 000 4, 000 DJIA (left scale) 1500 NASDAQ (right scale) 2, 000 0 1990 1000 500 0 1992 1994 1996 1998 2000 2002

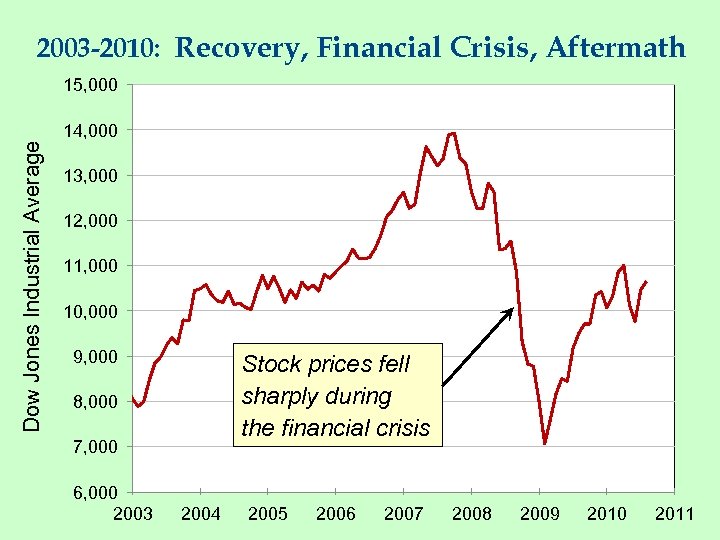2003 -2010: Recovery, Financial Crisis, Aftermath 15, 000 Dow Jones Industrial Average 14, 000 13, 000 12, 000 11, 000 10, 000 9, 000 Stock prices fell sharply during the financial crisis 8, 000 7, 000 6, 000 2003 2004 2005 2006 2007 2008 2009 2010 2011

Asset-price crashes § Crash: a rapid drop in asset prices not justified by interest rates or expected income. § Crashes often follow bubbles. § When a crash starts, panic sets in, more people sell, and prices plummet. CHAPTER 16 Asset Prices and Interest Rates 39

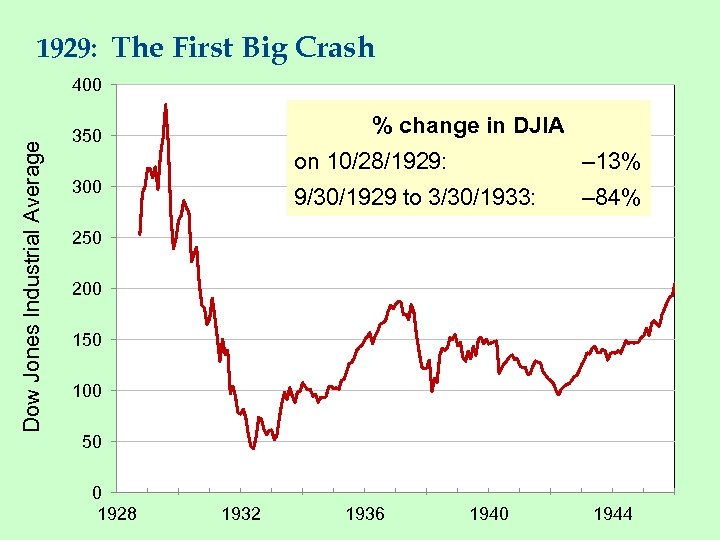1929: The First Big Crash Dow Jones Industrial Average 400 % change in DJIA 350 on 10/28/1929: 9/30/1929 to 3/30/1933: 300 – 13% – 84% 250 200 150 100 50 0 1928 1932 1936 1940 1944

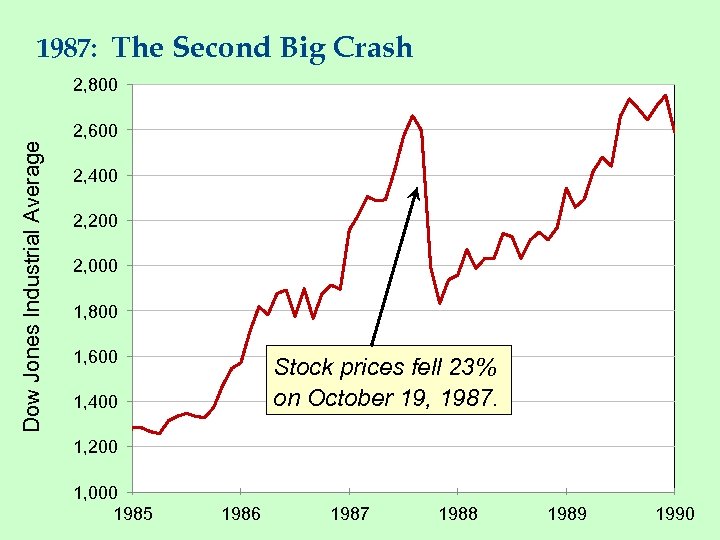1987: The Second Big Crash 2, 800 Dow Jones Industrial Average 2, 600 2, 400 2, 200 2, 000 1, 800 1, 600 Stock prices fell 23% on October 19, 1987. 1, 400 1, 200 1, 000 1985 1986 1987 1988 1989 1990

Crash prevention § Margin requirements: limits on the amount people can borrow to buy stocks § a response to the 1929 crash § intended to reduce bubbles § Circuit breakers: requirements that temporarily halt trading if prices fall sharply § a response to the 1987 crash § intended to reduce panic selling, giving people time to calm down and assess the value of their stocks CHAPTER 16 Asset Prices and Interest Rates 42

Measuring interest rates on bonds § What is “the interest rate” on the following bond? $4721. 09 = price to purchase bond today $5000. 00 = face value paid upon maturity in 2 years $100. 00 = annual coupon payment (starting in one year) § One measure of the interest rate is the yield to maturity (YTM): the interest rate that CHAPTER 16 Asset Prices and Interest Rates the present value equates the price of a bond with 43

Measuring interest rates on bonds § For the bond on the previous slide, the YTM is the interest rate that solves this equation: § Directly solving for YTM is generally not possible (except for zero-coupon bonds), so must either § use financial calculator, or § pick an interest rate, plug it in and see if it works; if not, try a different interest rate CHAPTER 16 Asset Prices and Interest Rates 44

NOW YOU TRY: Determining Yield to Maturity § In our example, the YTM is the value of i that solves this equation: § Plug i = 0. 04 into the right hand side. § If the result equals the left hand side, you have found the YTM. § Else, adjust i up or down by 0. 01 and try again. § Continue until you find YTM.

ANSWERS: Determining Yield to Maturity § First, try i = 0. 04: § At i = 0. 04, p. v. of payments > bond’s price, so YTM must be greater than 0. 04. Try 0. 05. § At i = 0. 05, p. v. of payments = bond’s price, so YTM = 0. 05.

The Rate of Return § Return on an asset: the capital gain or loss on an asset you own plus any payment you receive § Capital gain: the increase in your wealth from an increase in the asset’s price § Capital loss: the decrease in your wealth from a decrease in the price CHAPTER 16 Asset Prices and Interest Rates 47

The Rate of Return § Return on an asset: the capital gain or loss on an asset you own plus any payment you receive Return = (P 1 – P 0) + X, where P 0 = price paid for asset, P 1 = market price after one year, X = payment § Rate of return: return as a percentage of price CHAPTER 16 Asset Prices and Interest Rates 48

Rate of Return vs. Yield to Maturity § The most relevant interest rate is § YTM if holding the bond to maturity § Rate of return if selling the bond before maturity CHAPTER 16 Asset Prices and Interest Rates 49

Stock and Bond Returns, 1900 -2009 can f. I -4 i 6 e 1 sed ur l u Fig Bal ate ata plic e d Re th ind f

The Term Structure of Interest Rates § “Term” = time to a bond’s maturity § Term structure of interest rates: the relationships among interest rates on bonds with different maturities § We will learn the term structure in 3 steps: 1. Certainty: people know all future interest rates 2. Uncertainty: people must forecast future rates 3. Uncertainty with term premium: people adjust for risk associated with longer terms CHAPTER 16 Asset Prices and Interest Rates 51

Term structure under certainty § Assume people know all future interest rates. § The basic idea: Competition among bond sellers causes the rate on a two-year bond to equal an average of the two one-year rates that cover the same period. CHAPTER 16 Asset Prices and Interest Rates 52

Example § Buy a one-year bond today with YTM = 3%, then in one year use the proceeds to buy a one-year bond with YTM = 5%. In two years, you will have earned about 8%, or 4% per year. § You could also buy a two-year bond today, and competition should insure its annual YTM = 4%. CHAPTER 16 Asset Prices and Interest Rates 53

Term structure notation and formula Notation i 1(t ) = rate on 1 -period bond purchased in period t i 2(t ) = rate on 2 -period bond purchased in period t in(t ) = rate on n-period bond purchased in period t Formula for two periods i 2(t ) = (1/2) x [i 1(t ) + i 2(t +1)] Formula for n periods in(t ) = (1/n) x [i 1(t ) + i 1(t +1) + … + i 1(t +n – 1)] Under certainty, the n-period interest rate equals the average of the one-period rates prevailing in each of the n periods

Expectations theory of the term structure § Next, assume future interest rates are unknown. § The basic idea: Start with formula for term structure under certainty, but replace each future interest rate with its expected value. I. e. , people use forecasts of future rates since they do not know actual future rates. § We assume rational expectations: people optimally forecast future interest rates using all available information. CHAPTER 16 Asset Prices and Interest Rates 55

Expectations theory of the term structure § Notation: E X = expected value of some variable X E i 1(t +1) = the expected interest rate on a oneperiod bond purchased in period t + 1 E i 1(t +2) = the expected interest rate on a oneperiod bond purchased in period t + 2 § Formula: in(t ) = (1/n) x [i 1(t ) + E i 1(t +1) + … + E i 1(t + n – 1)] The n-period interest rate equals the average of the one-period rates expected to prevail in each of the n periods

Accounting for risk § Recall: changes in interest rates affect long-term bond prices more than short-term bond prices, making long-term bonds riskier than short-term bonds. § Holding long-term bonds requires a term premium, an extra return that compensates the bond holder. § τn = term premium on an n-period. § The longer the term, the greater the risk, so the larger the term premium: τ2 < τ3 < τ4 < … CHAPTER 16 Asset Prices and Interest Rates 57

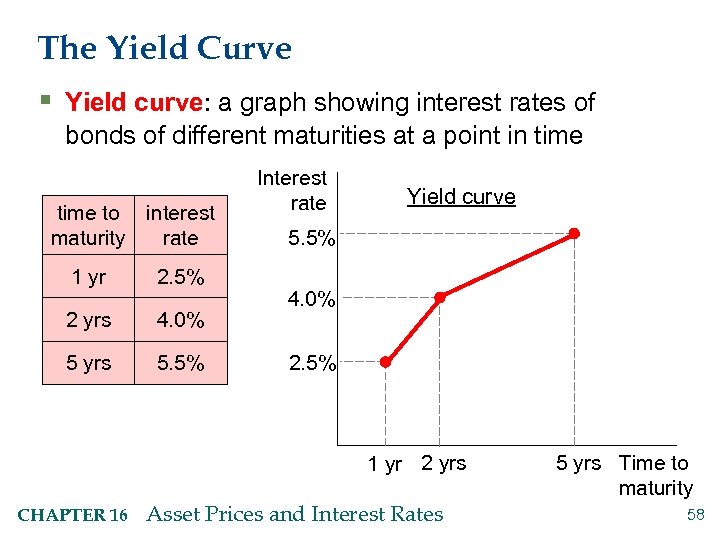The Yield Curve § Yield curve: a graph showing interest rates of bonds of different maturities at a point in time to interest maturity rate 1 yr 2. 5% 2 yrs 4. 0% 5 yrs 5. 5% Interest rate Yield curve 5. 5% 4. 0% 2. 5% 1 yr 2 yrs CHAPTER 16 Asset Prices and Interest Rates 5 yrs Time to maturity 58

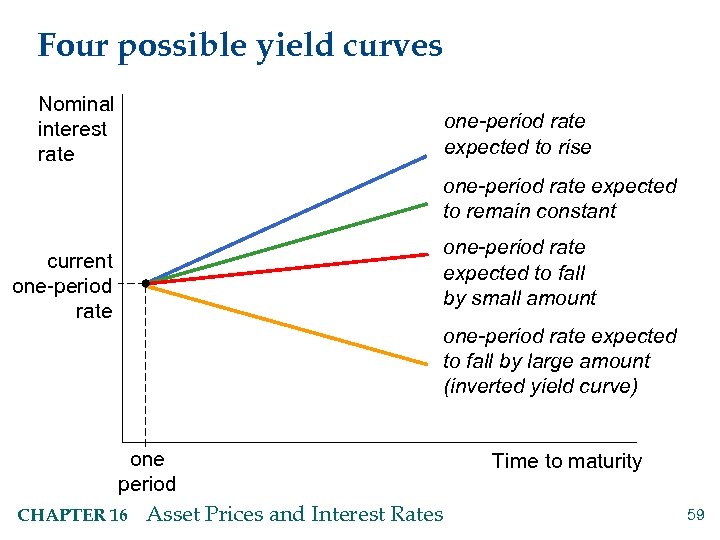Four possible yield curves Nominal interest rate one-period rate expected to rise one-period rate expected to remain constant one-period rate expected to fall by small amount current one-period rate expected to fall by large amount (inverted yield curve) one period CHAPTER 16 Asset Prices and Interest Rates Time to maturity 59

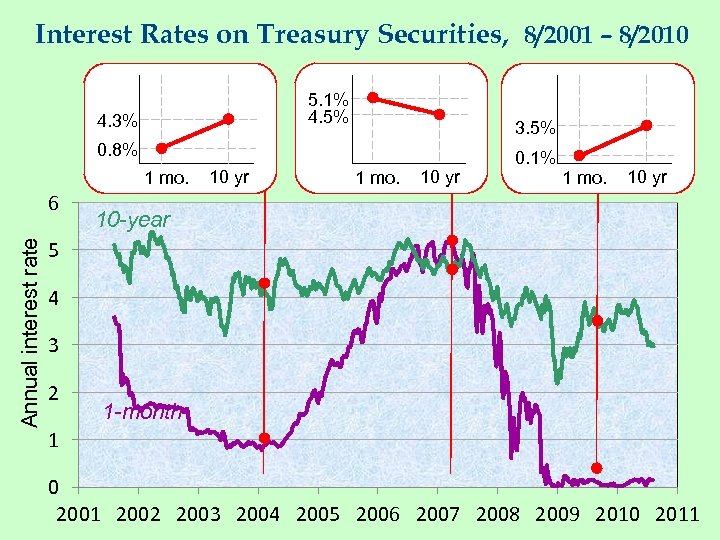Interest Rates on Treasury Securities, 8/2001 – 8/2010 5. 1% 4. 5% 4. 3% 3. 5% 0. 8% 1 mo. Annual interest rate 6 10 yr 1 mo. 10 yr 0. 1% 1 mo. 10 yr 10 -year 5 4 3 2 1 -month 1 0 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011

CHAPTER SUMMARY § The present value of a future sum is the amount that, if saved at the current interest rate, would equal the future sum. The higher the interest rate, the lower the present value of any given future sum. § The classical theory of asset prices states that the price of an asset equals the present value of the stream of payments the asset provides its owner. According to this theory, an asset’s price can change only if interest rates change or if there’s a change in expected payments. CHAPTER 16 Asset Prices and Interest Rates 61

CHAPTER SUMMARY § An asset-price bubble is a rapid increase in an asset’s price not justified by interest rates or expected earnings. People expect the price to rise, so they buy the asset, causing the price to rise. § An asset-price crash often occurs at the end of a bubble. Panic selling accelerates the fall in prices. § In response to big crashes in 1929 and 1987, margin requirements and circuit breakers were implemented to prevent future crashes or reduce their severity. CHAPTER 16 Asset Prices and Interest Rates 62

CHAPTER SUMMARY § A bond’s yield to maturity is the interest rate that equates the bond’s price with the present value of all payments its owner will receive. § The rate of return on a stock or bond equals the sum of payments and capital gains/losses in a year as a percentage of the price paid for the asset. § The Term Structure of Interest Rates is the relationship, at a point in time, among yields on bonds of various maturities. The Yield Curve depicts this relationship on a graph with interest rate on the vertical axis and time to maturity on the horizontal. CHAPTER 16 Asset Prices and Interest Rates 63

CHAPTER SUMMARY § The yield curve’s slope contains useful information about the market’s expectations: § If short-term interest rates are expected to remain constant, the yield curve will slope upward because longer-term bonds are riskier and carry a “term premium” to compensate bond holders for this risk. The term premium increases with yield to maturity. § A steeper yield curve indicates that short-term rates are expected to rise. § A flatter or “inverted” (downward-sloping) yield curve indicates that short-term rates are expected to fall, and often precedes an economic downturn. CHAPTER 16 Asset Prices and Interest Rates 64