Скачать презентацию Chapter 15 Option Valuation Option Values Скачать презентацию Chapter 15 Option Valuation Option Values

db681e726db5e4113554b6b9ed6eaae3.ppt

  • Количество слайдов: 18

Chapter 15 Option Valuation Chapter 15 Option Valuation

Option Values • Intrinsic value – • • Time value - Mc. Graw-Hill/Irwin © Option Values • Intrinsic value – • • Time value - Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

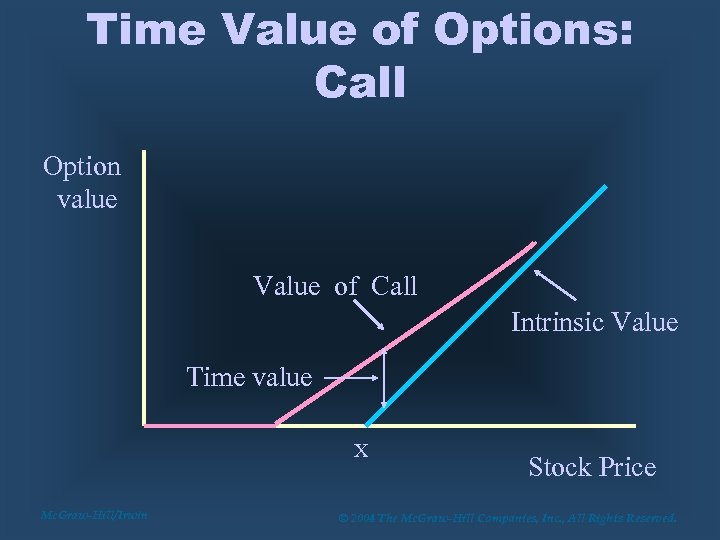Time Value of Options: Call Option value Value of Call Intrinsic Value Time value Time Value of Options: Call Option value Value of Call Intrinsic Value Time value X Mc. Graw-Hill/Irwin Stock Price © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

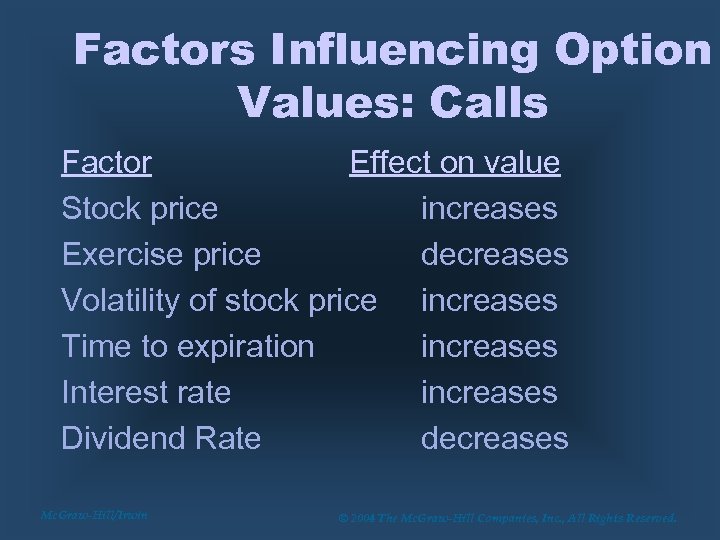Factors Influencing Option Values: Calls Factor Effect on value Stock price increases Exercise price Factors Influencing Option Values: Calls Factor Effect on value Stock price increases Exercise price decreases Volatility of stock price increases Time to expiration increases Interest rate increases Dividend Rate decreases Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Binomial Option Pricing: Text Example 200 100 75 C 50 Stock Price Mc. Graw-Hill/Irwin Binomial Option Pricing: Text Example 200 100 75 C 50 Stock Price Mc. Graw-Hill/Irwin 0 Call Option Value X = 125 © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Binomial Option Pricing: Text Example Alternative Portfolio Buy 1 share of stock at $100 Binomial Option Pricing: Text Example Alternative Portfolio Buy 1 share of stock at $100 Borrow $46. 30 (8% Rate) 53. 70 Net outlay $53. 70 Payoff Value of Stock Repay loan Net Payoff Mc. Graw-Hill/Irwin 150 0 Payoff Structure is exactly 2 times the Call © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Binomial Option Pricing: Text Example 150 53. 70 75 C 0 0 2 C Binomial Option Pricing: Text Example 150 53. 70 75 C 0 0 2 C = Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Another View of Replication of Payoffs and Option Values Alternative Portfolio - one share Another View of Replication of Payoffs and Option Values Alternative Portfolio - one share of stock and 2 calls written (X = 125) Portfolio is perfectly hedged Stock Value Call Obligation Net payoff Hence 100 - 2 C = 46. 30 or C = 26. 85 Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Black-Scholes Option Valuation Co = Soe-d. TN(d 1) - Xe-r. TN(d 2) d 1 Black-Scholes Option Valuation Co = Soe-d. TN(d 1) - Xe-r. TN(d 2) d 1 = [ln(So/X) + (r – d + s 2/2)T] / (s T 1/2) d 2 = d 1 - (s T 1/2) where Co = Current call option value. So = Current stock price N(d) = probability that a random draw from a normal dist. will be less than d. Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Black-Scholes Option Valuation X = Exercise price. d = Annual dividend yield of underlying Black-Scholes Option Valuation X = Exercise price. d = Annual dividend yield of underlying stock e = 2. 71828, the base of the natural log. r = Risk-free interest rate (annualizes continuously compounded with the same maturity as the option. T = time to maturity of the option in years. ln = Natural log function s = Standard deviation of annualized cont. compounded rate of return on the stock Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Call Option Example So = 100 X = 95 r =. 10 T =. Call Option Example So = 100 X = 95 r =. 10 T =. 25 (quarter) s =. 50 d = 0 d 1 = [ln(100/95)+(. 10 -0+(. 5 2/2))]/(. 5. 251/2) = d 2 =. 43 - ((. 5)(. 251/2) = Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Probabilities from Normal Dist. N (. 43) =. 6664 Table 17. 2 d N(d). Probabilities from Normal Dist. N (. 43) =. 6664 Table 17. 2 d N(d). 42. 6628. 43. 6664 Interpolation. 44. 6700 Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Probabilities from Normal Dist. N (. 18) =. 5714 Table 17. 2 d N(d). Probabilities from Normal Dist. N (. 18) =. 5714 Table 17. 2 d N(d). 16. 5636. 18. 5714. 20. 5793 Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Call Option Value Co = Soe-d. TN(d 1) - Xe-r. TN(d 2) Co = Call Option Value Co = Soe-d. TN(d 1) - Xe-r. TN(d 2) Co = 100 X. 6664 - 95 e-. 10 X. 25 X. 5714 Co = 13. 70 Implied Volatility Using Black-Scholes and the actual price of the option, solve for volatility. Is the implied volatility consistent with the stock? Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Put Option Value: Black. Scholes P=Xe-r. T [1 -N(d 2)] - S 0 e-d. Put Option Value: Black. Scholes P=Xe-r. T [1 -N(d 2)] - S 0 e-d. T [1 -N(d 1)] Using the sample data P = $95 e(-. 10 X. 25)(1 -. 5714) - $100 (1 -. 6664) P = $6. 35 Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Put Option Valuation: Using Put-Call Parity P = C + PV (X) - So Put Option Valuation: Using Put-Call Parity P = C + PV (X) - So = C + Xe-r. T - So Using the example data C = 13. 70 X = 95 S = 100 r =. 10 T =. 25 P = 13. 70 + 95 e -. 10 X. 25 - 100 P = 6. 35 Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Using the Black-Scholes Formula Hedging: Hedge ratio or delta The number of stocks required Using the Black-Scholes Formula Hedging: Hedge ratio or delta The number of stocks required to hedge against the price risk of holding one option Call = N (d 1) Put = N (d 1) - 1 Option Elasticity Percentage change in the option’s value given a 1% change in the value of the underlying stock Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.

Portfolio Insurance Protecting Against Declines in Stock Value • Buying Puts - • Limitations Portfolio Insurance Protecting Against Declines in Stock Value • Buying Puts - • Limitations • Mc. Graw-Hill/Irwin © 2004 The Mc. Graw-Hill Companies, Inc. , All Rights Reserved.