Chapter 15 Functional Programming Languages Chapter 15

Chapter 15 Functional Programming Languages

Chapter 15 Topics w w w w w Introduction Mathematical Functions Fundamentals of Functional Programming Languages The First Functional Programming Language: LISP Introduction to Scheme COMMON LISP ML Haskell Applications of Functional Languages Comparison of Functional and Imperative Languages 2

Introduction w The design of the imperative languages is based directly on the von Neumann architecture n Efficiency is the primary concern, rather than the suitability of the language for software development 3

Introduction w The design of the functional languages is based on mathematical functions n Based on theoretical basis mostly, but relatively unconcerned with the architecture of the machines on which programs will run 4

Lambda Expression w Lambda calculus is developed by Church 1941 w Square function is equivalent to lambda expressions (x) x * x w Application , (( (x) x * x)2) evaluates to 4. 5

Lambda Expression w According to Church, Lambda calculus (recursive definition): n n n Any identifier is lambda expression Function application If M and N are lambda expression, Application of M to N, written MN is also lambda expression Function abstraction M with parameter x An abstraction , x. M, where M is lambda expression, x is an identifier, is also lambda expression. 6

Lambda Expression w BNF Grammar rules for lambda calculus: w Example of lambda expression: Parameter, body Function application (MN) 7

Lambda Expression In lambda expression x. M : x identifier is said to be bound in M. Any identifier NOT bound in M is said to be free. w Bound variable is a place holder. They can be renamed consistently with ANY FREE variable. w Definition of free variable is w 8

Lambda Expression w Replace x with N substitution of an expression N for a variable x in M, written as M[N/x] is defined as: 1. 2. If free variables of N have NO bound occurrences in M, then M[N/x] is formed by replacing all free occurrences of x in M by N. Otherwise, assume that y is free in N and bound in M. l Consistently, replace the binding and corresponding bound occurrences of y in M by a new variable u. Repeat this renaming of bound variables in M until the condition in 1 is satisfied. Then proceed in Step 1. เปลยนชอ y in M เปนตวแปรใหม u กอน 9

Lambda Expression w Examples เปลยน y เปน x -rename x ทมอย (x เปน bound ใหเปลยนเปน -จากนนเปน y ทมเปน x ซงไมพบ y x u กอน ( 10

Lambda Expression w Meaning of lambda expression: Apply N to M -แทนคา x ดวย N )สง N เปน parameter แท w Evaluation of lambda expression is a derivation sequence w Example of evaluation Or we can evaluate from inner most Referential transparency 11

Mathematical Functions w Def: A mathematical function is a mapping of members of one set, called the domain set, to another set, called the range set 12

Mathematical Functions w Lambda expressions describe nameless functions w Lambda expressions are applied to parameter(s) by placing the parameter(s) after the expression e. g. ( (x) x * x)(3) which evaluates to 27 Just like the application of function…. 13

Mathematical Functions w Functional Forms n Def: A higher-order function, or functional form, is one that either takes functions as parameters or yields a function as its result, or both 14

Functional Forms 1. Function Composition n A functional form that takes two functions as parameters and yields a function whose value is the first actual parameter function applied to the application of the second Form: h f ° g which means h (x) f ( g ( x)) For f (x) x * x and g (x) x + 3, h f ° g yields (x + 3)* (x + 3) 15

Functional Forms 2. Construction n A functional form that takes a list of functions as parameters and yields a list of the results of applying each of its parameter functions to a given parameter Apply each parameter to each function Form: [f, g] For f (x) x * x and g (x) x + 3, [f, g] (4) yields (64, 7) f(4) g(4) 16

Functional Forms 3. Apply-to-all n A functional form that takes a single function as a parameter and yields a list of values obtained by applying the given function to each element of a list of parameters Form: For h (x) x * x ( h, (3, 2, 4)) yields (27, 8, 64) h(3) h(2) h(4) 17

Fundamentals of Functional Programming Languages w The objective of the design of a FPL is to mimic mathematical functions to the greatest extent possible w The basic process of computation is fundamentally different from that of an imperative language n n In an imperative language, operations are done and the results are stored in variables for later use Management of variables is a constant concern and source of complexity for imperative programming w In an FPL, variables are not necessary, as is the case 18 in mathematics

Fundamentals of Functional Programming Languages w In an FPL, the evaluation of a function always produces the same result given the same parameters n n This is called referential transparency Right-to-left/Left to Right DOESN’T matter since no concept of variable 19

LISP w Data object types: originally only atoms and lists w List form: parenthesized collections of sublists and/or atoms e. g. , (A B (C D) E) w Originally, LISP was a typeless language w LISP lists are stored internally as singlelinked lists 20

LISP w Lambda notation is used to specify functions and function definitions. Function applications and data have the same form. e. g. , the list --- (A B C) can mean q q list containing of three atoms, A, B, and C function application, meaning applying two parameters B, C to function A w The first LISP interpreter appeared only as a demonstration of the universality of the computational capabilities of the notation 21

Introduction to Scheme w A mid-1970 s dialect of LISP, designed to be a cleaner, more modern, and simpler version than the contemporary dialects of LISP w Uses only static scoping w Functions are first-class entities n n They can be the values of expressions and elements of lists They can be assigned to variables and passed as parameters 22

Introduction to Scheme w Primitive Functions 1. Arithmetic: +, -, *, /, ABS, SQRT, REMAINDER, MIN, MAX e. g. , (+ 5 2) yields 7 23

Introduction to Scheme 2. QUOTE -takes one parameter; returns the parameter without evaluation n n Normally, scheme interpreter, EVAL, evaluates parameters. QUOTE is used to avoid parameter evaluation when it is not appropriate QUOTE can be abbreviated with the apostrophe prefix operator e. g. , '(A B) is equivalent to (QUOTE (A B)) 24

Introduction to Scheme 3. CAR takes a list parameter; returns the first element of that list e. g. , (CAR '(A B C)) yields A (CAR '((A B) C D)) yields (A B) 4. CDR takes a list parameter; returns the list after removing its first element e. g. , (CDR '(A B C)) yields (B C) (CDR '((A B) C D)) yields (C D) 25

Introduction to Scheme 5. CONS takes two parameters, the first of which can be either an atom or a list and the second of which is a list; returns a new list that includes the first parameter as its first element and the second parameter as the remainder of its result e. g. , (CONS 'A '(B C)) returns (A B C) 26

Introduction to Scheme 6. LIST - takes any number of parameters; returns a list with the parameters as elements 27

Introduction to Scheme w Lambda Expressions n Form is based on notation e. g. , (LAMBDA (L) (CAR L))) L is called a bound variable w Lambda expressions can be applied e. g. , ((LAMBDA (L) (CAR L))) '((A B) C D)) 28

Introduction to Scheme w A Function for Constructing Functions DEFINE - Two forms: 1. To bind a symbol to an expression e. g. , (DEFINE pi 3. 141593) (DEFINE two_pi (* 2 pi)) 29

Introduction to Scheme 2. To bind names to lambda expressions e. g. , (DEFINE (cube x) (* x x x)) Example use: (cube 4) 30

Introduction to Scheme w Steps of evaluation process (for normal functions): 1. Parameters are evaluated, in no particular order** 2. The values of the parameters are substituted into the function body 3. The function body is evaluated 4. The value of the last expression in the body is the value of the function 31

Introduction to Scheme w Examples: (DEFINE (square x) (* x x)) (DEFINE (hypotenuse side 1) (SQRT (+ (square side 1) (square side 2))) ) 32

Introduction to Scheme w Predicate Functions: (#T is true and ()is false) 1. EQ? takes two symbolic parameters; it returns #T if both parameters are atoms and the two are the same e. g. , (EQ? 'A 'A) yields #T (EQ? 'A '(A B)) yields () n n Note that if EQ? is called with list parameters, the result is not reliable Also, EQ? does not work for numeric atoms Find out: How many equal functions does it have? 33

Introduction to Scheme w Predicate Functions: 2. LIST? takes one parameter; it returns #T if the parameter is a list; otherwise() 3. NULL? takes one parameter; it returns #T if the parameter is the empty list; otherwise() Note that NULL? returns #T if the parameter is() 4. Numeric Predicate Functions =, <>, >, <, >=, <=, EVEN? , ODD? , ZERO? , NEGATIVE? 34

Introduction to Scheme w Output Utility Functions: (DISPLAY expression) (NEWLINE) 35

Introduction to Scheme w Control Flow 1. Selection- the special form, IF (IF predicate then_exp else_exp) e. g. , (IF (<> count 0) (/ sum count) 0 ) 36

Introduction to Scheme w Control Flow 2. Multiple Selection - the special form, COND General form: (COND (predicate_1 expr {expr}). . . (predicate_1 expr {expr}) (ELSE expr {expr}) ) Returns the value of the last expr in the first pair whose predicate evaluates to true 37

Example of COND (DEFINE (compare x y) (COND ((> x y) (DISPLAY “x is greater than y”)) ((< x y) (DISPLAY “y is greater than x”)) (ELSE (DISPLAY “x and y are equal”)) ) ) 38

Example Scheme Functions 1. member - takes an atom and a simple list; returns #T if the atom is in the list; () otherwise (DEFINE (member atm lis) (COND ((NULL? lis) '()) ((EQ? atm (CAR lis)) #T) ((ELSE (member atm (CDR lis))) )) 39

Example Scheme Functions 2. equalsimp - takes two simple lists as parameters; returns #T if the two simple lists are equal; () otherwise (DEFINE (equalsimp lis 1 lis 2) (COND ((NULL? lis 1) (NULL? lis 2)) ((NULL? lis 2) '()) ((EQ? (CAR lis 1) (CAR lis 2)) (equalsimp(CDR lis 1)(CDR lis 2))) (ELSE '()) )) (a b c) 40

Example Scheme Functions 3. equal - takes two general lists as parameters; returns #T if the two lists are equal; ()otherwise (DEFINE (equal lis 1 lis 2) (COND ((NOT (LIST? lis 1))(EQ? lis 1 lis 2)) ((NOT (LIST? lis 2)) '()) ((a) (b)) ((NULL? lis 1) (NULL? lis 2)) ((NULL? lis 2) '()) ((equal (CAR lis 1) (CAR lis 2)) (equal (CDR lis 1) (CDR lis 2))) (ELSE '()) )) 41

Example Scheme Functions 4. append - takes two lists as parameters; returns the first parameter list with the elements of the second parameter list appended at the end (DEFINE (append lis 1 lis 2) (COND ((NULL? lis 1) lis 2) (ELSE (CONS (CAR lis 1) (append (CDR lis 1) lis 2))) )) 42

Introduction to Scheme w The LET function n General form: (LET ( (name_1 expression_1) (name_2 expression_2). . . (name_n expression_n)) body ) n Semantics: Evaluate all expressions, then bind the values to the names; evaluate the body 43

Introduction to Scheme (DEFINE (quadratic_roots a b c) (LET ( (root_part_over_2 a (/ (SQRT (- (* b b) (* 4 a c))) (* 2 a))) (minus_b_over_2 a (/ (- 0 b) (* 2 a))) (DISPLAY (+ minus_b_over_2 a root_part_over_2 a)) (NEWLINE) (DISPLAY (- minus_b_over_2 a root_part_over_2 a)) )) 44

Introduction to Scheme w Functional Forms 1. Composition - The previous examples have used it 2. Apply to All - one form in Scheme is mapcar - Applies the given function to all elements of the given list; result is a list of the results (DEFINE (mapcar fun lis) (COND ((NULL? lis) '()) (ELSE (CONS (fun (CAR lis)) (mapcar fun (CDR lis)))) )) 45

Introduction to Scheme w It is possible in Scheme to define a function that builds Scheme code and requests interpretation w This is possible because the interpreter is a user-available function, EVAL w e. g. , suppose we have a list of numbers that must be added together (DEFINE (adder lis) (COND ((NULL? lis) 0) (ELSE (+ (CAR lis) (adder(CDR lis )))) )) 46

Adding a List of Numbers ((DEFINE (adder lis) (COND ((NULL? lis) 0) (ELSE (EVAL (CONS '+ lis))) )) w The parameter is a list of numbers to be added; adder inserts a + operator and interprets the resulting list 47

Introduction to Scheme w Scheme includes some imperative features: 1. SET! binds or rebinds a value to a name 2. SET-CAR! replaces the car of a list 3. SET-CDR! replaces the cdr part of a list 48

COMMON LISP w A combination of many of the features of the popular dialects of LISP around in the early 1980 s w A large and complex language--the opposite of Scheme 49

COMMON LISP w Includes: n n n n records arrays complex numbers character strings powerful I/O capabilities packages with access control imperative features like those of Scheme iterative control statements 50

COMMON LISP w Example (iterative set membership, member) (DEFUN iterative_member (atm lst) (PROG () loop_1 (COND ((NULL lst) (RETURN NIL)) ((EQUAL atm (CAR lst))(RETURN T)) ) (SETQ lst (CDR lst)) (GO loop_1) )) 51

ML w A static-scoped functional language with syntax that is closer to Pascal than to LISP w Uses type declarations, but also does type inferencing to determine the types of undeclared variables (will see in Chapter 5) w It is strongly typed (whereas Scheme is essentially typeless) and has no type coercions w Includes exception handling and a module facility for implementing abstract data types 52

ML w Includes lists and list operations w The val statement binds a name to a value (similar to DEFINE in Scheme) w Function declaration form: function_name (formal_parameters) = function_body_expression; e. g. , fun cube (x : int) = x * x; 53

Haskell w Similar to ML (syntax, static scoped, strongly typed, type inferencing) w Different from ML (and most other functional languages) in that it is purely functional (e. g. , no variables, no assignment statements, and no side effects of any kind) 54

Haskell w Most Important Features n n Uses lazy evaluation (evaluate no subexpression until the value is needed) Has list comprehensions, which allow it to deal with infinite lists 55

Haskell Examples 1. Fibonacci numbers (illustrates function definitions with different parameter forms) fib 0 = 1 fib 1 = 1 fib (n + 2) = fib (n + 1) + fib n 56

Haskell Examples 2. Factorial (illustrates guards) fact n | n == 0 = 1 | n > 0 = n * fact (n - 1) The special word otherwise can appear as a guard 57

Haskell Examples 3. List operations List notation: Put elements in brackets e. g. , directions = [“north”, “south”, “east”, “west”] n Length: # Size of list e. g. , #directions is 4 n Arithmetic series with the. . operator e. g. , [2, 4. . 10] is [2, 4, 6, 8, 10] n 58

Haskell Examples 3. List operations (cont) Catenation is with ++ e. g. , [1, 3] ++ [5, 7] results in [1, 3, 5, 7] n CONS, CAR, CDR via the colon operator (as in Prolog) CONS e. g. , 1: [3, 5, 7] results in [1, 3, 5, 7] n 59

Haskell Examples product of empty list = 1 product [] = 1 product (a: x) = a * product x Tail part of list x is a list product(a. . x) = a * product(x) fact n = product [1. . n] product of a*. . *x fact(n) = product (1. . n) 60

Haskell Examples 4. List comprehensions: set notation e. g. , [n * n | n ← [1. . 20]] computes the square of 1, the square of 2, …the square of 20 factors n = [i | i ← [1. . n div 2], n mod i == 0] for i=1 to n/2 compute (return n mod i This function computes all of the factors of its given parameter 61

Haskell Examples w Quicksort: Sort of empty list = empty sort [] = [] sort (a: x) = sort [b | b ← x; b <= a] Sort of list [a. . x] is sort for all element b’s that is <= a ++ [a] ++pivot a is sort [b | b ← x; b > a] sort for all element b’s that is > a 62

Haskell Examples 5. Lazy evaluation e. g. , Positive number starts from 0 positives = [0. . ] Squares is list of [02 12 22…] squares = [n * n | n ← [0. . ]] (only compute those that are necessary) e. g. , member squares 16 would return True 16 is a member of squares or not 63

Haskell Examples w The member function could be written as: member [] b = False b is not a member of empty list return false member(a: x) b=(a == b)||member x b B is member of (a. . x) or not -return if a==b or member x b --make recursive all squares = [n * n | n ← [0. . ]] (only compute those that are necessary) e. g. , member squares 16 would return True 64

Haskell Examples squares = [n * n | n ← [0. . ]] (only compute those that are necessary) e. g. , member squares 16 w However, this would only work if the parameter to squares was a perfect square; if not, it will keep generating them forever (due to lazy evaluation). The following version will always work: member 2 (m: x) n If m < n | m < n = member 2 x n | m == n = True If m equals to n, will return true. | otherwise = False If m < n, will make a recursive ca Otherwise will return false. 65

Applications of Functional Languages w APL is used for throw-away programs w LISP is used for artificial intelligence n n Knowledge representation Machine learning Natural language processing Modeling of speech and vision w Scheme is used to teach introductory programming at a significant number of universities 66

Comparing Functional and Imperative Languages w Imperative Languages: n n Efficient execution Complex semantics Complex syntax Concurrency is programmer designed w Functional Languages: n n Simple semantics Simple syntax Inefficient execution Programs can automatically be made concurrent 67

Chapter 16 Logic Programming Languages

Chapter 16 Topics w w w w Introduction A Brief Introduction to Predicate Calculus and Proving Theorems An Overview of Logic Programming The Origins of Prolog The Basic Elements of Prolog Deficiencies of Prolog Applications of Logic Programming

Introduction w Logic programming language or declarative programming language w Express programs in a form of symbolic logic w Use a logical inferencing process to produce results w Declarative rather that procedural: n only specification of results are stated (not detailed procedures for producing them)

Introduction to Predicate Calculus w Proposition: a logical statement that may or may not be true n Consists of objects and relationships of objects to each other

Introduction to Predicate Calculus w Symbolic logic can be used for the basic needs of formal logic: n n n express propositions express relationships between propositions describe how new propositions can be inferred from other propositions w Predicate calculus is a particular form of symbolic logic used for logic programming.

Propositions w Objects in propositions are represented by simple terms: either constants or variables w Constant: a symbol that represents an object w Variable: a symbol that can represent different objects at different times n different from variables in imperative languages

Propositions w Atomic propositions consist of compound terms w Compound term: one element of a mathematical relation, written like a mathematical function n n Mathematical function is a mapping Can be written as a table

Propositions w Compound term composed of two parts n n Functor: function symbol that names the relationship Ordered list of parameters (tuple) w Examples: Functor(order list of parameters) student(jon) like(seth, OSX) like(nick, windows) like(jim, linux)

Propositions w Propositions can be stated in two forms: n n Fact: proposition is assumed to be true Query: truth of proposition is to be determined w Compound proposition: n n Have two or more atomic propositions Propositions are connected by operators

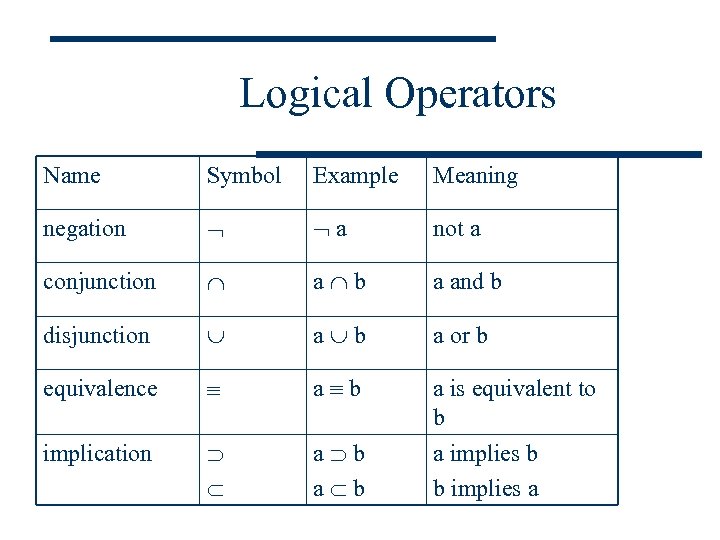Logical Operators Name Symbol Example Meaning negation a not a conjunction a b a and b disjunction a b a or b equivalence a b a is equivalent to b implication a b a implies b b implies a

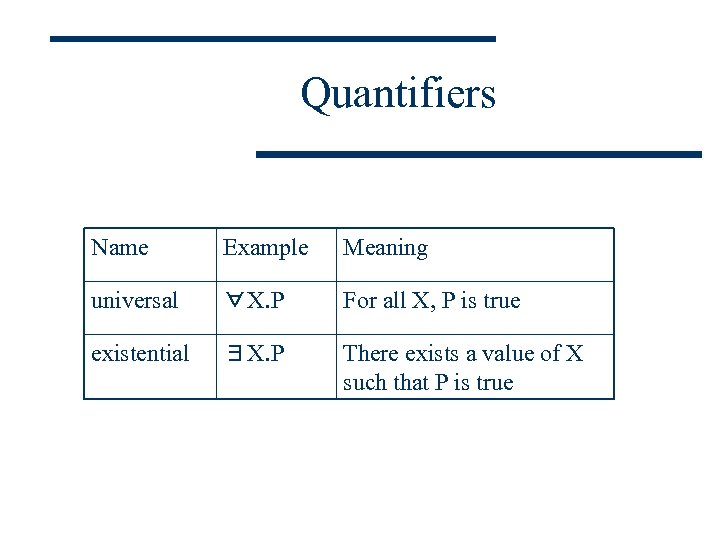Quantifiers Name Example Meaning universal ∀X. P For all X, P is true existential ∃X. P There exists a value of X such that P is true

Clausal Form w. Too many ways to state the same thing w. Use a standard form for propositions w. Clausal form: Anticedent Consequence B 1 B 2 … B n A 1 A 2 … Am means if all the As are true, then at least one B is true w. Antecedent: right side w. Consequent: left side

Predicate Calculus and Proving Theorems w A use of propositions is to discover new theorems that can be inferred from known axioms and theorems w Resolution: an inference principle that allows inferred propositions to be computed from given propositions

Resolution หาคำตอบ ใหตวแปรใน proposition w Unification: finding values for variables in propositions that allows matching process to succeed กำหนดคาใหตวแปรใน proposition เพอทดสอบวาใชคำตอบหรอ w Instantiation: assigning temporary values to variables to allow unification to succeed w After instantiating a variable with a value, if matching fails, may need to backtrack and instantiate with a different value

Theorem Proving w Use proof by contradiction w Hypotheses: a set of pertinent propositions w Goal: negation of theorem stated as a proposition w Theorem is proved by finding an inconsistency

Theorem Proving w Basis for logic programming w When propositions used for resolution, only restricted form can be used w Horn clause - can have only two forms Prolog conseq : single n n Headed: single atomic proposition on left side Headless: empty left side (used to state facts) w Most propositions can be stated as Horn clauses

Overview of Logic Programming w Declarative semantics n n There is a simple way to determine the meaning of each statement Simpler than the semantics of imperative languages w Programming is nonprocedural n Programs do not state now a result is to be computed, but rather the form of the result

Example: Sorting a List w Describe the characteristics of a sorted list, not the process of rearranging a list consequence Antecedents sort(old_list, new_list) permute (old_list, new_list) sorted (new_list) sorted (list) ∀j such that 1 j < n, list(j) list (j+1)

The Origins of Prolog w University of Aix-Marseille n Natural language processing w University of Edinburgh n Automated theorem proving

The Basic Elements of Prolog w w w Edinburgh Syntax Term: a constant, variable, or structure Constant: an atom or an integer Atom: symbolic value of Prolog Atom consists of either: n n a string of letters, digits, and underscores beginning with a lowercase letter a string of printable ASCII characters delimited by apostrophes

The Basic Elements of Prolog w Variable: any string of letters, digits, and underscores beginning with an uppercase letter w Instantiation: binding of a variable to a value n Lasts only as long as it takes to satisfy one complete goal w Structure: represents atomic proposition functor(parameter list)

Fact Statements w Used for the hypotheses w Headless Horn clauses student(jonathan). sophomore(ben). brother(tyler, cj). มแต consequence

Rule Statements w Used for the hypotheses w Headed Horn clause w Right side: antecedent (if part) n May be single term or conjunction w Left side: consequent (then part) n Must be single term w Conjunction: multiple terms separated by logical AND operations (implied) 16 -90

Rule Statements parent(kim, kathy): - mother(kim, kathy). w Can use variables (universal objects) to generalize meaning: parent(X, Y): - mother(X, Y). sibling(X, Y): - mother(M, X), mother(M, Y), father(F, X), father(F, Y).

Goal Statements w For theorem proving, theorem is in form of proposition that we want system to prove or disprove – goal statement w Same format as headless Horn student(james) w Conjunctive propositions and propositions with variables also legal goals father(X, joe) สำหรบ query

Inferencing Process of Prolog w Queries are called goals w If a goal is a compound proposition, each of the facts is a subgoal w To prove a goal is true, must find a chain of inference rules and/or facts. For goal Q: B : - A C : - B … Q : - P Eg. Forward chaining w Process of proving a subgoal called matching, satisfying, or resolution

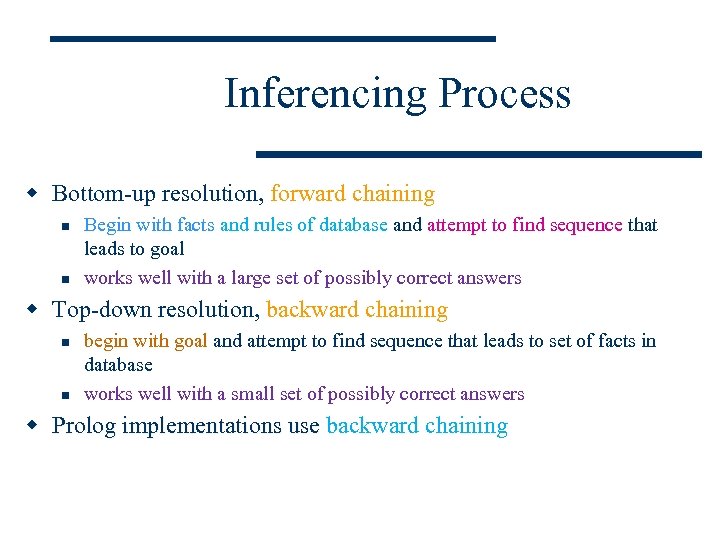Inferencing Process w Bottom-up resolution, forward chaining n n Begin with facts and rules of database and attempt to find sequence that leads to goal works well with a large set of possibly correct answers w Top-down resolution, backward chaining n n begin with goal and attempt to find sequence that leads to set of facts in database works well with a small set of possibly correct answers w Prolog implementations use backward chaining

Inferencing Process w When goal has more than one subgoal, can use either n n Depth-first search: find a complete proof for the first subgoal before working on others Breadth-first search: work on all subgoals in parallel w Prolog uses depth-first search n Can be done with fewer computer resources

Inferencing Process w With a goal with multiple subgoals, if fail to show truth of one of subgoals, reconsider previous subgoal to find an alternative solution: backtracking w Begin search where previous search left off w Can take lots of time and space because may find all possible proofs to every subgoal

Simple Arithmetic w Prolog supports integer variables and integer arithmetic w is operator: takes an arithmetic expression as right operand variable as left operand w A is B / 10 + C w Not the same as an assignment statement!

Example speed(ford, 100). speed(chevy, 105). speed(dodge, 95). speed(volvo, 80). time(ford, 20). time(chevy, 21). time(dodge, 24). time(volvo, 24). distance(X, Y) : - speed(X, Speed), time(X, Time), Y is Speed * Time.

Trace w Built-in structure that displays instantiations at each step w Tracing model of execution - four events: n n Call (beginning of attempt to satisfy goal) Exit (when a goal has been satisfied) Redo (when backtrack occurs) Fail (when goal fails)

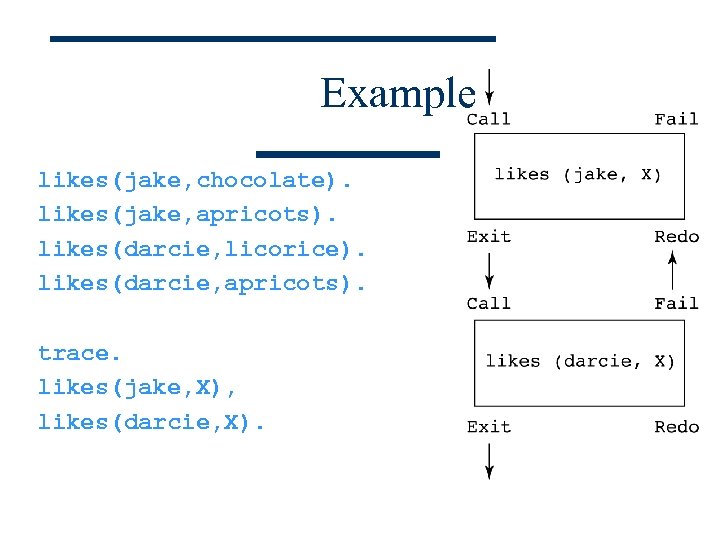Example likes(jake, chocolate). likes(jake, apricots). likes(darcie, licorice). likes(darcie, apricots). trace. likes(jake, X), likes(darcie, X).

List Structures w Other basic data structure (besides atomic propositions we have already seen): list w List is a sequence of any number of elements w Elements can be atoms, atomic propositions, or other terms (including other lists) [apple, prune, grape, kumquat] [] (empty list) [X | Y] (head X and tail Y)

Example w Definition of append function: append([], List). append([Head | List_1], List_2, [Head | List_3]) : append (List_1, List_2, List_3).

Example w Definition of reverse function: reverse([], []). reverse([Head | Tail], List) : reverse (Tail, Result), append (Result, [Head], List).

Deficiencies of Prolog w Resolution order control w The closed-world assumption w The negation problem w Intrinsic limitations

Applications of Logic Programming w Relational database management systems w Expert systems w Natural language processing w Education

Conclusions w Advantages: n n n Prolog programs based on logic, so likely to be more logically organized and written Processing is naturally parallel, so Prolog interpreters can take advantage of multi-processor machines Programs are concise, so development time is decreased – good for prototyping

Readings and Testing about Prolog • http: //www. doc. gold. ac. uk/~mas 02 g w/prolog_tutorial/prologpages/ • http: //www. gprolog. org/manual/gpr olog. html

Intro to Logic Programming by Prolog Prepared by Manuel E. Bermúdez, Ph. D. Associate Professor University of Florida

Logic Programming Fundamentals w Horn clauses: n General form: H B 1, B 2, . . . Bn n Meaning: if B 1, B 2, . . . Bn are true, then H is true. w Deductive reasoning: C A, B D C D A, B

Resolution w Process of deriving new statements, combining old ones, cancelling like terms, etc. w Variables may acquire values through unification. More later. w Example: fun(X) sunny(X) sunny(Florida) fun(Florida)

Prolog Fundamentals w All Prolog programs built from terms: n n Programs The data manipulated by programs w Three types of terms: n n n Constants: integers, real numbers, atoms. Variables. Compound terms.

Prolog Fundamentals (cont’d) w Constants: Integers, e. g. 123; Reals, e. g. : 1. 23 w Atoms: n n n Lexically, a lowercase letter followed by any number of additional letters, digits or underscores, e. g. foobar, 'Hello'. Atoms do look like variables in other languages, but foobar is not a variable; it has no binding, it is a unique value. An atom can also be sequence of punctuation characters: *, . , =, @#$

Prolog Fundamentals (cont’d) w Variables: begin with an upper-case letter, e. g. X, My_var. w Can be instantiated (take on a value) at run time. w Variables can start with an underscore, and get special treatment.

Prolog Fundamentals (cont’d) w A compound term, or structure, consists of an atom called a functor, and a list of arguments, e. g. sunny(florida), weird(prolog), related(jim, john). No space allowed w A compound term may look like a function call, but it isn’t. It is structured data, or logical facts.

Syntax for Terms : : = || : : = | | : : = ( ) : : = | , w Even an arithmetic expression, usually written as 1+2, is just an abbreviation for +(1, 2).

The Prolog Database w A Prolog system maintains a collection of facts and rules of inference, a database. w A Prolog program is just a “store” of facts for this database. w The simplest item in the database is a fact: a term followed by a period: sunny(florida). sunny(california). father(jim, ann).

Simple Queries ? - sunny(florida). Yes. ? - father(jim, ann). Yes. ? - father(jim, tom). No. ? - sunny(X). Attempt to match X. X = florida; Type a semi-colon, and X = california; the system tries again. No. This time it fails.

Lists w w Similar to Lisp. [a, b, c] is syntactic sugar. Separate head from tail using ‘|’. ‘. ’ similar to ‘cons’ in Lisp. List notation [] [1, 2, 3] [1, parent(X, Y)] Term denoted []. (1, []). (1, . (2, . (3, []))). (1, . (parent(X, Y), [])) [1|X] [1, 2|[3, 4]] . (1, X). (1, . (2, X))) [1, 2, 3, 4]

Pattern Matching: Unification. Examples: [george, X] unifies with [george, tom] [X, fred, [1, X]] unifies with [jane, fred, [1, Y]] by Y = X = jane [X, fred, [1, X]] does not unify with [jane, fred, [1, ralph]], because X cannot match both jane and ralph.

Unification 1. A constant unifies only with itself. 2. Two structures unify iff they have • • • The same functor. The same number of arguments. The arguments unify recursively. 3. A variable X unifies with anything. The other thing could: • • have a value. So, instantiate X. be an uninstantiated variable. Link the two variables, so that: l If either is instantiated later, they both share the value.

Example of Unification Unify ([p, q, [c, X]], [Y, q, [X, c]]) = Unify(p, Y) and Unify([q, [c, X]], [q, [X, c]]) = (Y=p) and Unify(q, q) and Unify( [[c, X]], [[X, c]]) = (Y=p) and Unify( [c, X], [X, c]) and Unify(nil, nil) = (Y=p) and Unify(c, X) and Unify([X], [c]) = (Y=p) and (X=c) and Unify(X, c) and Unify(nil, nil) =

Example of Unification (cont’d) (Y=p) and (X=c) and Unify(valueof(X), c) = (Y=p) and (X=c) and Unify(c, c) = (Y=p) and (X=c).

Some Useful Predicates w The predicate append(X, Y, Z) is true iff appending Y onto the end of X yields Z. Z=[X Y] Examples: ? - append([1, 2], [3, 4], X). X = [1, 2, 3, 4] Yes. ? - append(X, [3, 4], [1, 2, 3, 4]). X = [1, 2] Yes.

Some Useful Predicates (cont’d) w append can be used with any pattern of instantiation (that is, with variables in any position). Example: ? - append(X, [3, 4], [1, 2, 3, 4]). X = [1, 2] Yes

Some Useful Predicates (cont’d) Example: ? - append(X, Y, [1, 2, 3]). X = [] Y = [1, 2, 3] ; X = [1] Y = [2, 3] ; X = [1, 2] Y = [3] ; X = [1, 2, 3] Y = [] ; No.

Other Predefined List Predicates Predicate Description member(X, Y) Provable if list Y contains element X. select(X, Y, Z) Provable if list Y contains element X, and removing X from Y yields Z. Provable if Z is the Xth element of list Y, counting from 0. Provable if X is a list of length Y. nth 0(X, Y, Z) length(X, Y) w Queries using these predicates can contain variables anywhere.

Sample Use of select Z= ? - select(2, [1, 2, 3], Z). list [1 2 3] that is removed 2. =[1 3] Z = [1, 3] ; No. ? - select(2, Y, [1, 3]). Y = [2, 1, 3] ; Y = [1, 2, 3] ; Y = [1, 3, 2] ; No.

Prolog Rules (or maybe not : -) w Rules are of the form predicate : - conditions. w The predicate is true iff all conditions are true. w Conditions appear as a list of terms, separated by commas.

Prolog Rules (cont’d) w The simplest rules are facts: Father. Of(john, ted). Mother. Of(connie, ted). Father. Of(fred, carol). Mother. Of(connie, carol). Father. Of(ted, ken). Mother. Of(jane, ken). Father. Of(ted, lloyd). Mother. Of(alice, lloyd) Father. Of(lloyd, jim). Mother. Of(carol, jim). Father. Of(lloyd, joan). Mother. Of(carol, joan). n Note: male/female names are meaningless.

Prolog Rules (cont’d) w More complex rules: Parent. Of(X, Y) : - Father. Of(X, Y). Parent. Of(X, Y) : - Mother. Of(X, Y). Alternatives are attempted in the order specified: ? - Parent. Of(connie, ted). First, match Father. Of(connie, ted). Fails. Then, match Mother. Of(connie, ted). Succeed.

Prolog Rules (cont’d) w Using variables, we can get answers: ? - Parent. Of(ted, C) C = ken; C = lloyd; No. ? - Parent. Of(P, carol) P = fred; P = connie; No.

Prolog Rules (cont’d) w Using more than one condition: Grand. Parent(X, Y) : - Parent. Of(X, Z), Parent. Of(Z, Y). ? - Gran. Parent(G, jim) Prolog performs a backtracking, depth-first, left-to-right search for values to satisfy the predicate(s) sought.

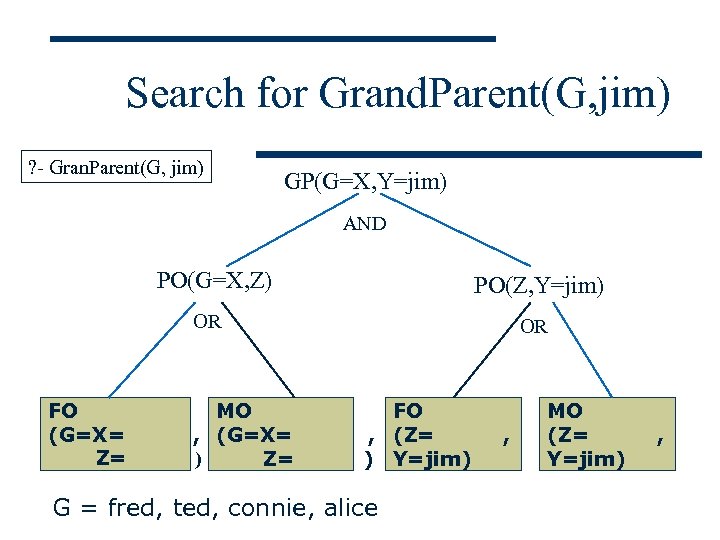Search for Grand. Parent(G, jim) ? - Gran. Parent(G, jim) GP(G=X, Y=jim) AND PO(G=X, Z) PO(Z, Y=jim) OR FO (G=X= Z= MO , (G=X= ) Z= OR FO , (Z= ) Y=jim) G = fred, ted, connie, alice , MO fff (Z= Y=jim) ,

Another example w Facts: Author. Of("Life on a Donkey", "Swartz"). Author. Of("Big and Little", "Jones"). Author. Of("Where are We", "White"). Author. Of("In a Pig’s Eye", "Brown"). Author. Of("High Flight", "Smith"). Subject. Of("Life on a Donkey", travel). Subject. Of("Big and Little", life). Subject. Of("Where are We", life). Subject. Of("In a Pig’s Eye", travel). Subject. Of("High Flight", bio).

Another example (cont’d) w More facts: Audience. Of("Life on a Donkey", adult). Audience. Of("Big and Little", child). Audience. Of("Where are We", teen). Audience. Of("In a Pig’s Eye", adult). Audience. Of("High Flight", adult).

Selecting Reviewers w Would like an author who: n has written books on the same subject. Reviewer(Book, Person) : Subject. Of(Book, Sub), Subject. Of(Another. Book, Sub), Author. Of(Another. Book, Person), not Author. Of(Book, Person).

Selecting Reviewers (cont’d) n If someone who has written in the same subject is not available, then find someone who has written for the same audience. Reviewer(Book, Person) : Audience. Of(Book, Aud), Audience. Of(Another. Book, Aud), Author. Of(Another. Book, Person), not Author. Of(Book, Person). Exercise: Find reviewers for “Life on a Donkey”. Hint: There are 3. A reviewer can qualify twice.