Chapter 15 Apportionment Part 6 Huntington-Hill Method

Chapter 15: Apportionment Part 6: Huntington-Hill Method

Huntington-Hill Method • This method is similar to both the Jefferson and Webster Methods. The Huntington-Hill, Webster and Jefferson methods are all called “divisor methods” because of the way in which a critical divisor is used to determine the apportionment. • Like the other divisor methods, the Huntington-Hill method begins by determining a standard divisor and then calculating a quota for each state. • Next, in the Huntington-Hill method, instead of rounding the quota in the usual way, we round to get the initial apportionments in a way that is based on a calculation involving the geometric mean of two numbers. • Given two numbers a and b, the geometric mean of these numbers is

Geometric Mean • We can visualize the geometric mean in two ways. Here is the first way: • Suppose we have two numbers a and b. What is the geometric mean of these two numbers ? • The geometric mean of a and b is the length of the side of a square who area is equal to the area of a rectangle with sides a and b. a b

Geometric Mean • Here is another way to visualize the geometric mean of two numbers. • Suppose we have two numbers a and b. What is the geometric mean of these two numbers ? • The geometric mean of a and b is the length of the perpendicular segment connecting a point on the diameter of a circle with diameter length a + b to a point on that circle. a b

Geometric Mean • Here is another way to visualize the geometric mean of two numbers. • Suppose we have two numbers a and b. What is the geometric mean of these two numbers ? • The geometric mean of a and b is the length of the perpendicular segment connecting a point on the diameter of a circle with diameter length a + b to a point on that circle. Length is geometric mean of a and b a b

Huntington-Hill Method • To determine how to round q, we must calculate the geometric mean of each state’s upper and lower quota. If q is less than this geometric mean, we round down. If q is equal or greater than the geometric mean, we round up. • Let q* represent the geometric mean of the upper and lower quota of q. That is, • We define << q >> to be the result of rounding q using the geometric mean. • Thus

Huntington-Hill Method • Back to the Huntington-Hill Method … • First, we calculate the standard divisor. Then we calculate q, the initial apportionment for each state. • Next, we round q using the geometric mean method. • Then, we determine if seats must be added or removed to result in the desired apportionment. • If seats must be added or removed, we must choose a modified divisor, as in the Jefferson and Webster method, so that rounding the resulting quotas by the geometric-mean method will produce the required total.

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population A 453 B 367 C 697 total 1517

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population A 453 B 367 C 697 total 1517 We calculate the standard divisor first… In this case, s = p/h = 1517/75 = 20. 2267

Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population q A 453/s = 22. 3962 B 367/s = 18. 1444 C 697/s = 34. 4595 total 1517 75 We must calculate the standard divisor first. In this case, s = p/h=1517/75 = 20. 2267 Now we can calculate the quota for each state … q = pi/s

Example: Huntington-Hill Method • Here, we are calculating q*, which is the geometric mean of the upper and lower quota for each state. State population q A 453/s = 22. 3962 B 367/s = 18. 1444 C 697/s = 34. 4595 total 1517 75 q*

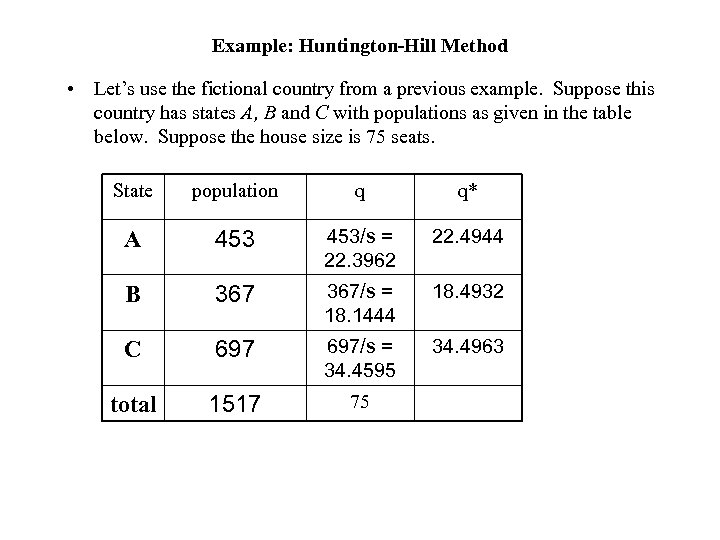Example: Huntington-Hill Method • Let’s use the fictional country from a previous example. Suppose this country has states A, B and C with populations as given in the table below. Suppose the house size is 75 seats. State population q q* A 453/s = 22. 3962 22. 4944 B 367/s = 18. 1444 18. 4932 C 697/s = 34. 4595 34. 4963 total 1517 75

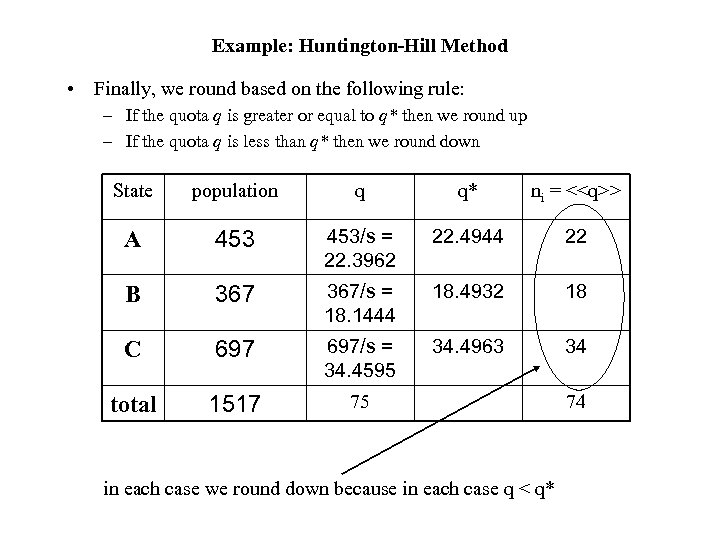Example: Huntington-Hill Method • Finally, we round based on the following rule: – If the quota q is greater or equal to q* then we round up – If the quota q is less than q* then we round down State population q q* ni = <> A 453/s = 22. 3962 22. 4944 22 B 367/s = 18. 1444 18. 4932 18 C 697/s = 34. 4595 34. 4963 34 total 1517 75 in each case we round down because in each case q < q* 74

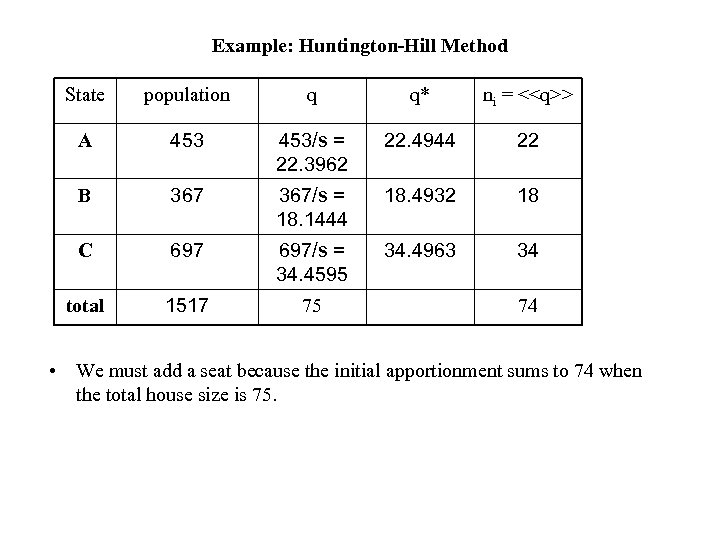Example: Huntington-Hill Method State population q q* ni = <> A 453/s = 22. 3962 22. 4944 22 B 367/s = 18. 1444 18. 4932 18 C 697/s = 34. 4595 34. 4963 34 total 1517 75 74 • We must add a seat because the initial apportionment sums to 74 when the total house size is 75.

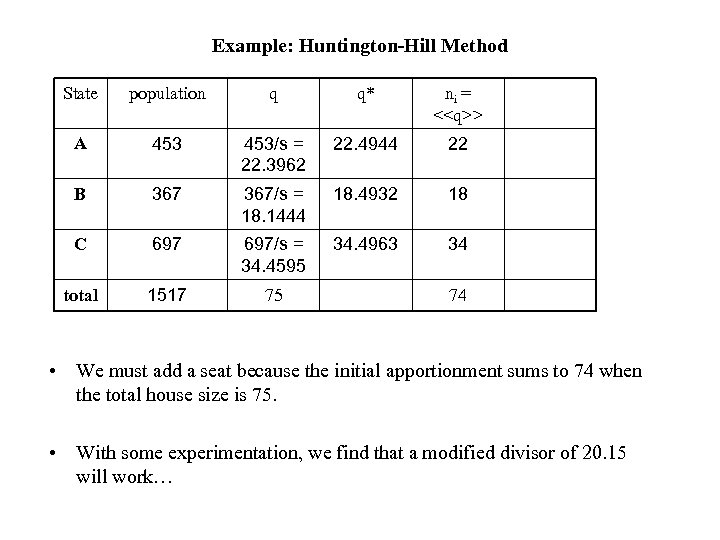Example: Huntington-Hill Method State population q q* ni = <> A 453/s = 22. 3962 22. 4944 22 B 367/s = 18. 1444 18. 4932 18 C 697/s = 34. 4595 34. 4963 34 total 1517 75 74 • We must add a seat because the initial apportionment sums to 74 when the total house size is 75. • With some experimentation, we find that a modified divisor of 20. 15 will work…

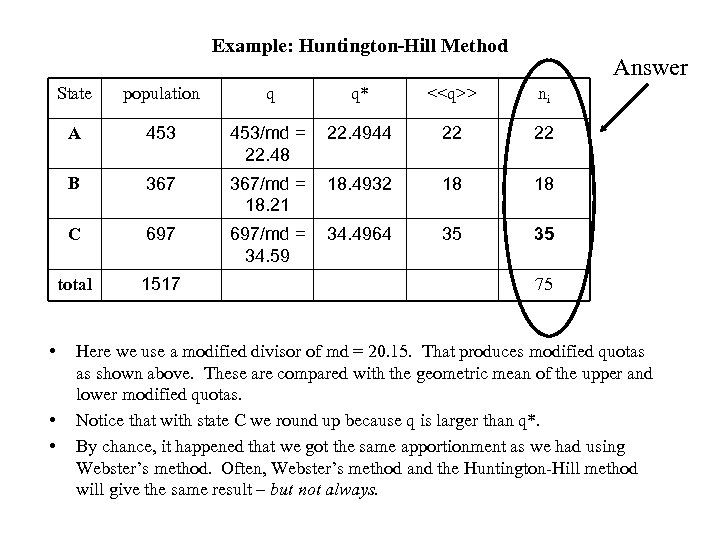Example: Huntington-Hill Method Answer State q* <> ni 453/md = 22. 48 22. 4944 22 22 B 367/md = 18. 21 18. 4932 18 18 C 697/md = 34. 59 34. 4964 35 35 total • • q A • population 1517 75 Here we use a modified divisor of md = 20. 15. That produces modified quotas as shown above. These are compared with the geometric mean of the upper and lower modified quotas. Notice that with state C we round up because q is larger than q*. By chance, it happened that we got the same apportionment as we had using Webster’s method. Often, Webster’s method and the Huntington-Hill method will give the same result – but not always.